变比为3的交-交升压型开关电容变换器研究

赵　锐，郭　倩，包莅庭，蔡　慧

(中国计量大学 机电工程学院，浙江 杭州 310018)

开关电容变换器属于一种没有磁性元件的变换器.因为组成它的元件仅是一些电容和功率开关管，所以电路结构简单.其中电容是核心的储能元件，功率开关管的导通能实现电容的充电和放电，因此只要控制开关管的导通时间就可以达到电能转换的目的.该变换器有很多的优点，它的结构十分简单，输出效率高，而且功率密度大[1].该变换器的概念问世以来[2]，各种拓扑结构[3-4]以及控制方法层出不穷[5-8].开关电容变换器在汽车工业[9-10]和电池工业[11-12]等方面获得广泛应用.文献[13-14]首次将开关电容原理引入交-交静态转换领域，极高的变换效率以及较稳定的电压变比证明了其优越性.

开关电容原理的早期研究[15]指出, 等效内阻决定了开关电容变换器的稳态性能.根据文献[16]提出的状态空间平均法，把整体电路分成不同局部电路，将电容两端的电压或者流过电感的电流视为状态变量列写出状态方程，再通过加权平均的方法得出输出方程.但是其表达式中没有开关频率这一重要变量.降压型开关电容变换器的等效内阻表达式在文献[17]中提出，但是这种方法难以用在大规模电路，并且没有完善对开关频率变量的分析.在不同充电和放电工作方式下，开关电容变换器的性能是不同的，其性能在文献[18]中提出.但是不适用于高阶的变换器网络.以上工作都没有对工作于交-交升压状态的开关电容变换器进行分析研究.

本文在以上研究工作的基础上，通过结合状态空间平均法，以暂态分析的方法对变比为3的交-交升压型开关电容变换器进行数学建模，研究变换器电路各参数对于变换器稳态性能的影响.

1　升压型开关电容变换器

1.1　变换器电路

本文所述的开关电容变换器如图1.主电路由6组MOSFET (Metal-Oxide-Semiconductor Field-Effect Transistor, 金属氧化物半导体场效应晶体管)开关组和5个电容组成.其中电容C4和C5确保电容C1和C3之间的电压平衡；每2个共源极的MOSFET构成1组MOSFET.该变换器的主要特点如下：1)能实现直-直变换；2)不含磁性元件，结构简单，效率和功率密度高；3)可以双向传输能量，既可用于升压变换，又可用于降压变换(本文主要分析交-交升压变换的情况)；4)能实现交-交变换;5)控制驱动方式简单.

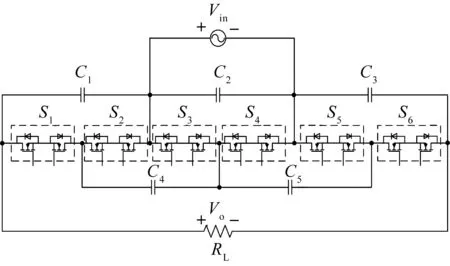
图1　升压型开关电容变换器Figure 1　Step-up switched-capacitor converter

图2显示了该变换器的栅极驱动信号.开关电容变换器的效率和输出电压变比在占空比0.5时达到最佳.具体的分析将在后文中阐述.

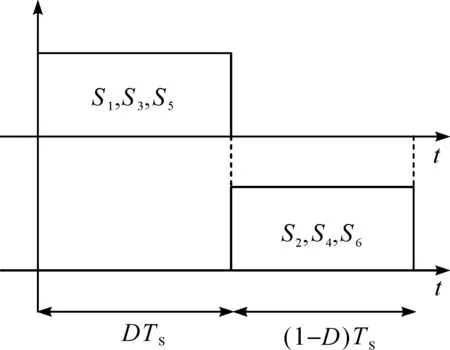
图2　PWM门极驱动波形Figure 2　Waveform of PWM gate drive

1.2　工作过程

本变换器的工作过程如图3.在一个开关周期中，以MOSFET开关组的关断导通为根据，电路分为两个工作状态.由于该变换器拓扑的对称性，现以输入电源为正半周期的情况下对变换器进行工作过程分析，变换器在电源正半周的工作过程描述如下：

工作状态1：如图3(a)，开关组S1,S3,S5导通，开关组S2,S4,S6关断.电容C4给电容C1充电，电源通过电容C2给电容C5充电，电容C3放电.该状态结束后，开关组S2,S4,S6导通，开关组S1,S3,S5关断.

工作状态2：如图3(b)，开关组S1,S3,S5关断，开关组S2,S4,S6导通.电容C5给电容C3充电，电源通过电容C2给电容C4充电，电容C1放电.该状态结束后，开关组S1,S3,S5导通，开关组S2,S4,S6导通.

在整个开关周期中，电容C2保持充电至输入电压状态.

图3　开关电容变换器工作过程Figure 3　Operation Stages of SCC

根据开关周期和回路的时间常数，开关电容变换器可分为3种工作模式：完全充电(Complete Charge,CC)，部分充电(Partial Charge,PC)和不充电(No Charge,NC)[18].开关电容变换器处于三种工作模式下电容充电电流波形如图4所示.CC模式下电容充电会产生较大的尖峰电流，增加电路的导通损耗，所以CC模式下比PC和NC模式变换器的效率低，变换器的理想工作状态是工作于PC和NC模式.NC模式与PC模式相比没有明显的优势，且NC模式需要极高的开关频率和较大的电容，不易于实现，因此电路参数的选取要尽量使变换器处于PC工作模式下.

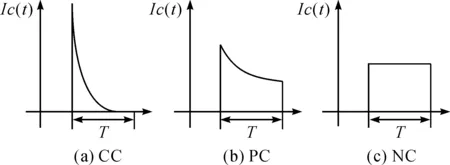
图4　变换器在三种工作模式下的电容充电电流波形Figure 4　Capacitor charge current waveform ofconverter in three operating modes

图5显示了该变换器工作于PC模式下的主要电流电压波形.

图5　电容理论工作波形Figure 5　Theoretical capacitors operation waveforms

2　理论分析

2.1　建模分析

由于变换器拓扑的对称性，现只对工作状态1进行建模分析.通过以上对变换器电路工作状态1的分析以及考虑观察分析的方便性，现将图3(a)的电路以开关组S3所在的支路为中心线等效的分解成两个局部电路，其中IL为流过RL的电流，具体电路如图6.其中图6(a)表示变换器电容C1和C4的局部电路，其中图6(b)表示变换器电容C2和C5的局部电路.

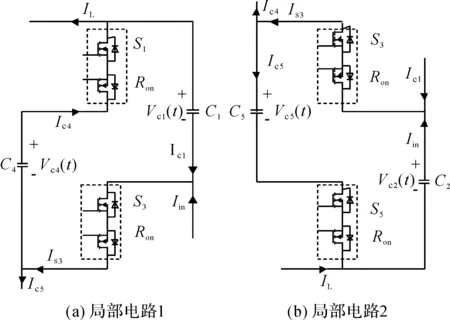
图6　变换器局部电路Figure 6　Sub-circuits of SCC

在变换器电路的理论分析过程中，为简化计算过程，记C1=C2=C3=C4=C5=C.每组MOSFET的导通内阻为Ron，其中Ron的大小是单个MOSFET通态电阻Rdson的2倍).

由图6(a)中的局部电路1，当t∈[0,DTs]时有：

(1)

由基尔霍夫电流定律，有

(2)

对如图6(b)所示的电容C5的充电回路，有

(3)

考虑边界条件，有

Vc1(0)=Vc1min.

(4)

Vc4(0)=Vc4max.

(5)

Vc5(0)=Vc5min.

(6)

由电量平衡，有

(7)

(8)

考虑到电路结构的对称性，有

Vo=Vc1max+Vc1min+Vin.

(9)

联立式(1)-(9)，得到电压变比的表达式

(10)

其中C为各电容值，R为充电回路中的阻性成分(主要由MOSFET的通态电阻Ron组成，由于拓扑的对称性，流经电容C4和C5的电流有效值相同，因此开关S3上的电流是C4和C5电流的2倍,有R=3Ron)，Ts为PWM驱动的开关周期，D为PWM驱动的占空比，RL为变换器负载.

根据式(10)，有

(11)

即变换器空载时，其理想电压变比为3.

根据文献[19]，开关电容变换器可由如图7所示的理想等效电路表示.

图7　开关电容变换器等效电路Figure 7　Equivalent circuit of SCC

因此，有

(12)

根据式(11)和式(12)，可以得到变换器等效内阻Req的表达式

(13)

2.2　电路参数分析

通过上一节的公式(10)，分析电容值C，MOSFET通态电阻Ron，负载大小，开关频率fs和占空比D等参数对变换器性能产生的影响.

如果没有特别说明，所分析变换器元件参数如表1.

表1　变换器元件参数表

图8给出占空比与电压变比的关系.显然当占空比到0.5时，电压变比为最大值.而当占空比时在小于0.1或大于0.9的时候，电压变比迅速下降.当占空比在0.4～0.6时，对电压变比的控制作用较不明显.

图8　电压变比与占空比Figure 8　Voltage gain and duty cycle

图9给出开关频率、电压变比和电容值之间的关系.显著影响着变换器的性能的是电容值的改变.更大的电容值和更高的开关频率使得电容充放电的ΔVc(=Vc max-Vc min)更小[20]，更高的充电效率和更好的变换器性能.但是开关频率也不能无限制提高，其调制作用存在饱和现象;由于等效串联电感和开关损耗的存在，过高的开关频率反而会影响性能.

图10给出了电压变比和负载大小之间的关系.显然当负载超过100 Ω时，电压变比趋于稳定，并接近于3.当负载小于20 Ω时，电压变比迅速下降.

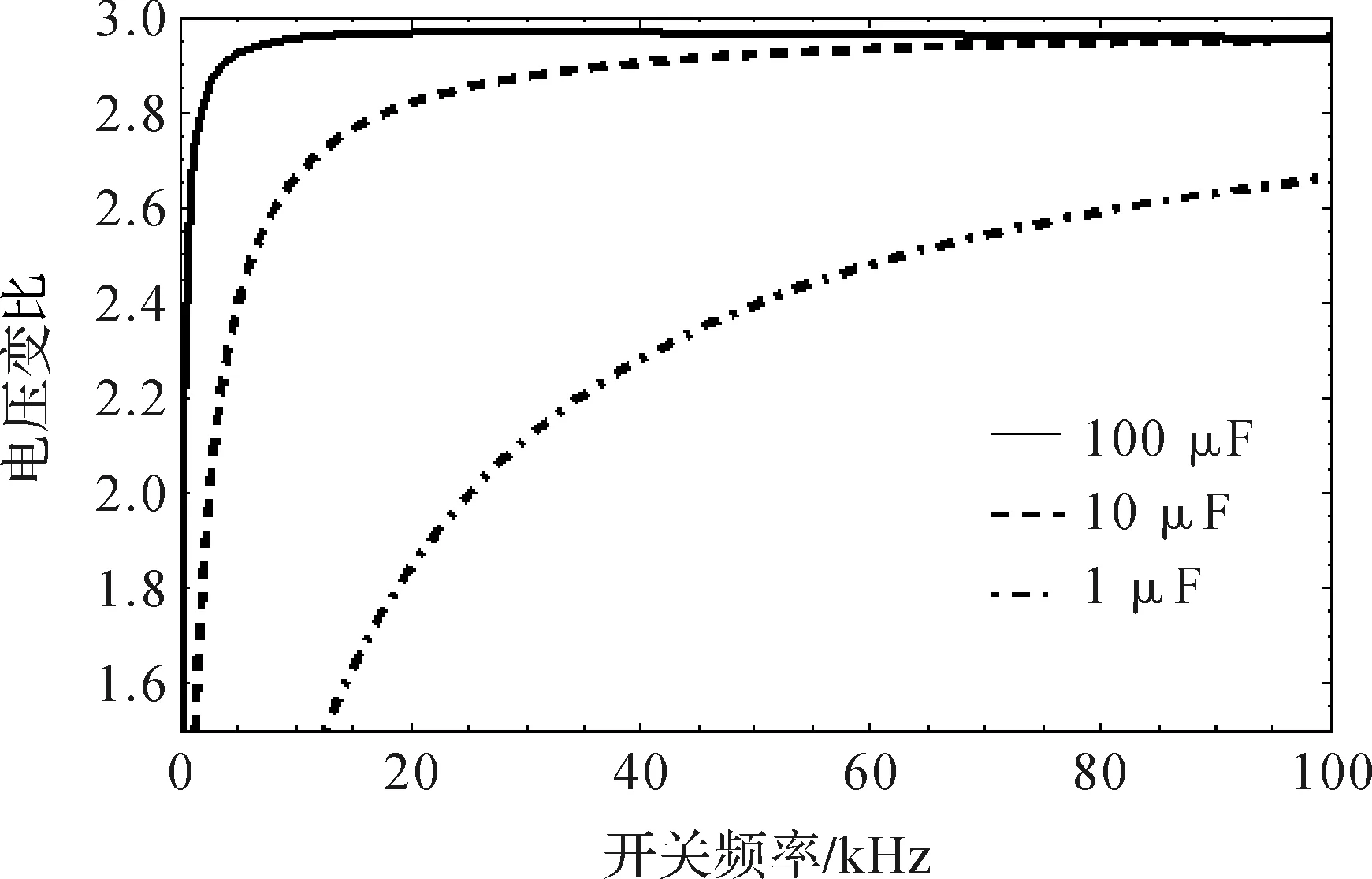
图9　电压变比与开关频率Figure 9　Voltage gain and switching frequency

图10　电压变比与负载大小Figure 10　Voltage gain and load size

图11给出电压变比和充电回路电阻之间的关系.较大的回路电阻将使电容充放电电流减小，延长充电时间.在选元件时，通态电阻较小的MOSFET为首选.电容回路的充电常数τc=2RC与充电时间存在以下关系：当τc>Ts，电容处于不充电模式下；当τc≈Ts，电容处于部分充电模式下.在这两种工作模式下，该变换器输出变比较大[18].

图11　电压变比与回路电阻Figure 11　Voltage gain and loop resistance

3　实验结果分析

为了验证理论的分析结果是否正确，搭建了一个1 kW，73/220 V的样机进行实验验证.所用PWM驱动开关频率为50 kHz，占空比为0.5.MOSFET管采用FQA62N25C，其通态电阻的典型值为0.035 Ω.电容C1,C2和C3采用20 μF的MPE薄膜电容.负载采用50 Ω功率电阻.

图12　实验输入输出电压波形Figure 12　Experimental waveforms ofinput and output voltages

变换器工作时的输入和输出电压波形如图12所示.以75 V交流输入电压(50 Hz)为例，测得电压有效值为215.65 V，电压变比为2.875.

图13　电容C1电流实验波形Figure 13　Experimental waveform of currentthrough capacitor C1

图13给出了变换器工作时流经电容C1的电流波形，与图5(b)理论工作波形一致.

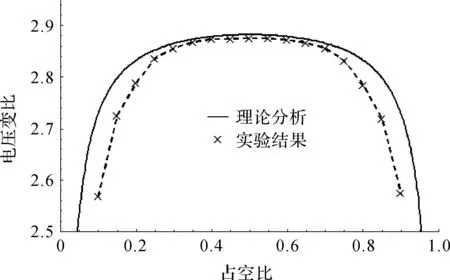
图14　电压变比与占空比的实验与理论曲线Figure 14　Experimental and theoreticalcurves of voltage gain and duty cycle

图14对比了电压变比随占空比变化的理论分析和实验结果.当占空比在0.2～0.8之间时，两者较一致.在极端占空比条件下，两者误差较大.这主要是由于实际情况下PWM驱动信号的上升、下降时间以及死区时间等因素增大造成的，实际的占空比与设定值相差较大，此时的结果已不具有参考性.

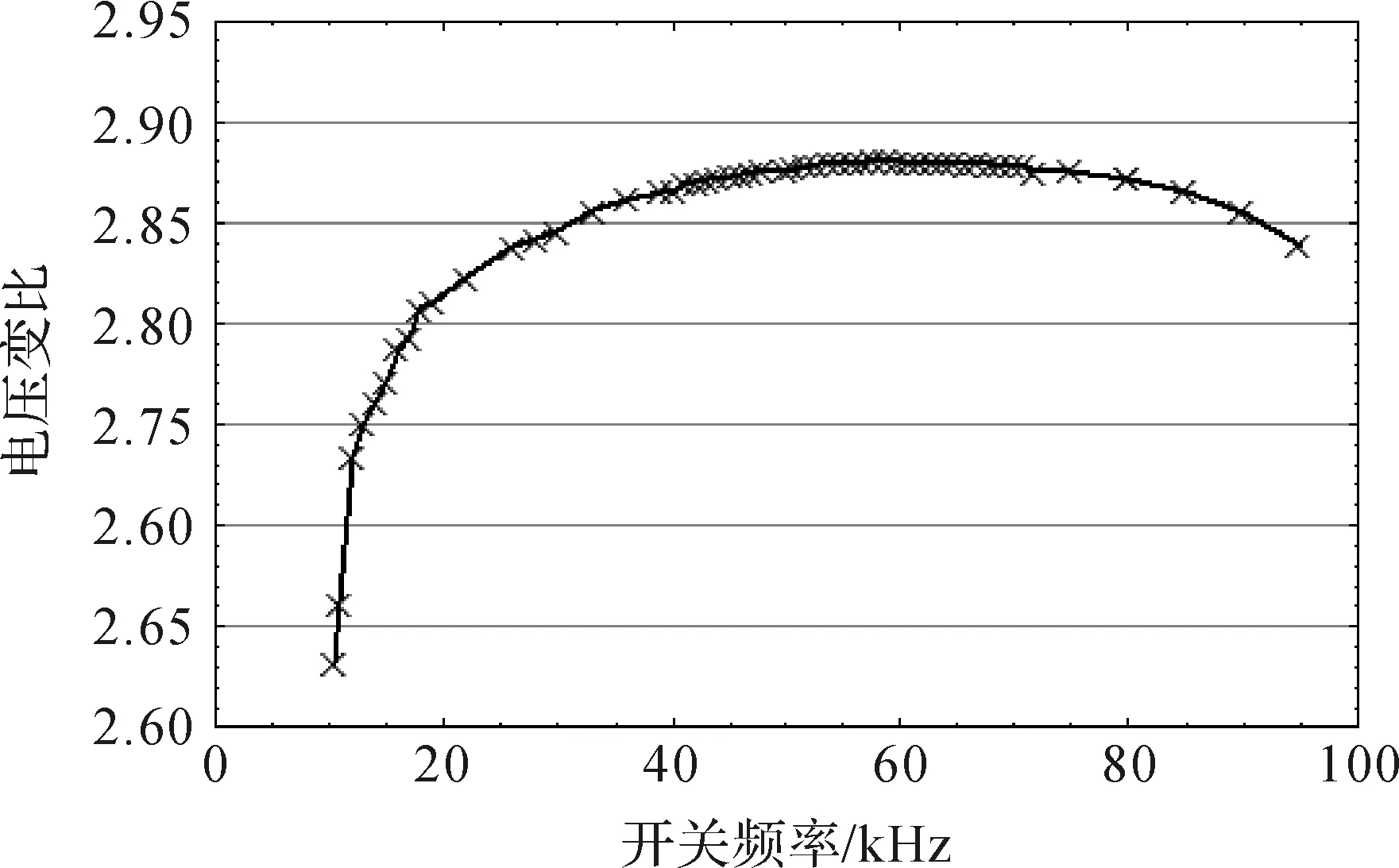
图15　电压变比与开关频率(实验曲线)Figure 15　Voltage gain and switching frequency(experimental curve)

图15给出电压变比与开关频率的实验曲线.在10 kHz到60 kHz范围之内，随着开关频率增高电压变比也随着增大；高于60 kHz后，由于开关损耗和寄生因素等影响，电压变比随开关频率的升高而下降.

图16　效率与输出功率(实验曲线)Figure 16　Efficiency and output power(experimental curve)

图16给出变换器效率与输出功率的实验曲线.随输出功率的增大，变换器效率逐渐升高.峰值效率为87.25%.

4　结　论

本文讨论研究了一种变比为3的交-交升压型开关电容变换器.通过结合暂态分析的方法建立了该变换器的数学模型，并给出了等效内阻和变换器稳态变比关于电容C，开关频率Ts，占空比D和MOSFET通态电阻Ron的解析分析.最后搭建了该变换器的样机，经过实验验证了理论分析的正确性.该方法还可以为更高阶的开关电容变换器的分析提供理论基础.

【参考文献】

[1]丘东元,张波.开关电容变换器组成原理及发展趋势[J].电气应用,2007,26(9):6-12.

QIU D Y, ZHANG B. The composition principle and development trend of switched-capacitor converters[J].ElectrotechnicalApplication, 2007,26(9):6-12.

[2]MAKOWSKI M S, MAKSIMOVIC D. Performance limits of switched capacitor DC-DC converters[C]//IEEEPowerElectronicsSpecialistConference. Atlanta: IEEE, 1995:1215-1221.

[3]XIONG S, WONG S C, TAN S C, et al. A family of exponential step-down switched-capacitor converters and their applications in two-stage converters[J].IEEETransactionsonPowerElectronics, 2014,29(4):1870-1880.

[4]WU B, LI S, SMEDLEY K M. A family of two-switch boosting switched-capacitor converters[J].IEEETransactionsonPowerElectronics,2015,30(10):5413-5424.

[5]TAN S C, KIRATIPONGVOOT S, BRONSTEIN S, et al. Adaptive mixed on-time and switching frequency control of a system of interleaved switched-capacitor converters[J].IEEETransactionsonPowerElectronics, 2011,26(2):364-380.

[6]KIRATIPONGVOOT S, TAN S C, IOINOVICI A. Switched-capacitor converters with multiphase interleaving control[C]//IEEEEnergyConversionCongressandExposition. Phoenix: IEEE,2011:1156-1161.

[7]MILEIKO S, KUSHNEROV A, SOKOLOV D, et al. Self-timed control of two-phase switched capacitor converters[C]//IEEEInternationalConferenceontheScienceofElectricalEngineering. Eilat: IEEE,2016:1-4.

[8]YANG L, ZHANG X B, WU B, et al. A nonlinear control for switched-capacitor converter based on one-cycle control technique[C]//IEEETransportationElectrificationConferenceandExpo(ITEC). Dearborn: IEEE,2016:1-5.

[9]ZHANG F, DU L, PENG F Z, et al. A new design method for high-power DC-DC converters[J].IEEETransactionsonPowerElectronics, 2008,23(2):832-840.

[10]AMJADI Z, WILLIAMSON S S. A novel control technique for a switched-capacitor-converter-based hybrid electric vehicle energy storage system[J].IEEETransactionsonIndustrialElectronics, 2010,57(3):926-934.

[11]CAO Y, LEI Y, PILAWA-PODGURSKI R C N, et al. Modular switched-capacitor DC-DC converters tied with lithium-ion batteries for use in battery electric vehicles[C]//IEEEEnergyConversionCongressandExposition. Montreal: IEEE, 2015:85-91.

[12]YE Y, CHENG K W E. Modeling and analysis of series-parallel switched-capacitor voltage equalizer for battery/supercapacitor strings[J].IEEEJournalofEmergingandSelectedTopicsinPowerElectronics, 2015,3(4):977-983.

[13]LAZZARIN T B, ANDERSEN R L, MARTINS G B, et al. A 600-W switched-capacitor AC-AC converter for 220 V/110 V and 110 V/220 V applications[J].IEEETransactionsonPowerElectronics, 2012,27(12):4821-4826.

[14]ANDERSEN R L, LAZZARIN T B, BARBI I. A 1-kW step-up/step-down switched-capacitor AC-AC converter[J].IEEETransactionsonPowerElectronics, 2013,28(7):3329-3340.

[15]SEEMAN M D, SANDERS S R. Analysis and optimization of switched-capacitor DC-DC converters[J].IEEETransactionsonPowerElectronics, 2008,23(2):841-851.

[16]MIDDLEBROOK R, SLOBODAN C. A general unified approach to modelling switching-converter power stages[C]//IEEEPowerElectronicsSpecialistConference. Cleveland: IEEE,1976:18-34.

[17]KIMBALL J W, KREIN P T. Analysis and design of switched capacitor converters[C]//IEEEAppliedPowerElectronicsConferenceandExposition. Austin: IEEE, 2005:1473-1477.

[18]BEN-YAAKOV S. Behavioral average modeling and equivalent circuit simulation of switched capacitors converters[J].IEEETransactionsonPowerElectronics, 2012,27(2):632-636.

[19]OOTA I, HARA N, UENO F. A general method for deriving output resistances of serial fixed type switched-capacitor power supplies[C]//IEEEInternationalSymposiumonCircuitsandSystems. Geneva: IEEE, 2000:503-506.

[20]CHEUNG C K, TAN S C, TSE C K, et al. On energy efficiency of switched-capacitor converters[J].IEEETransactionsonPowerElectronics, 2013,28(2):862-876.