一种基于fp-tree的Apriori算法改进研究

倪政君，夏哲雷

(中国计量大学 信息工程学院，浙江 杭州 310018)

关联规则挖掘是数据挖掘中一个重要的研究领域,本质上是对频繁项集的挖掘，主要研究从事务数据库、关系型数据库或数据仓库等海量数据的项集之间，发现有价值的频繁出现的模式关联和相关性.关联规则挖掘最早仅限于事务数据库的布尔型关联规则，现已被广泛使用于关系型数据库中，因此，积极对挖掘关联规则挖掘进行研究具有重要的意义[1].

关联规则挖掘算法大致可以分为两类：一种是Apriori类算法，如基于压缩矩阵的NCM_Apriori算法[2]、基于Hash的DHP算法[3]等等，这些算法都是在经典的Apriori算法[4]上进行改进，算法步骤相对简单并且易于实现；但是这些算法都需要重复扫描数据库用来统计候选项集支持数，在数据库数据量较大时，这些算法的挖掘速度较低.另一类算法是基于树形结构的关联规则算法，如基于fp-tree的FP-Growth算法[5]、基于cofi-tree的COFI-Tree算法[6]、基于cfp-tree的CT-PRO算法[7].该类算法采用树形结构对数据进行压缩，并对子树进行挖掘，挖掘时没有候选项集的生成，减少了扫描数据的量，算法的挖掘速度得到提升；但是，该类算法在子树挖掘时可能会递归生成大量的子树，当在递归生成子树上耗费太多时间时，会使得算法的挖掘速度受到限制.

一些研究人员结合两类算法的优点，将fp-tree树形结构移植到Apriori算法当中，提出了基于fp-tree的改进Apriori算法[8-9].这类改进算法先采用fp-tree对数据进行压缩，仅仅需要扫描数据库一次或者两次，然后把生成的fp-tree划分成若干子数据集分区，再将子数据集分区结合Apriori算法的候选项集生成机制进行挖掘.此类算法大幅减少了候选项集支持数统计的扫描数据量，算法的挖掘速度得到提高.文献[8]结合fp-tree将fp-tree进行压缩，并从最不频繁项元开始划分生成子树，单独地在每一颗子树上采用候选项集生成机制进行挖掘.该算法避免了递归生成大量子树，并且减少了数据扫描量，挖掘速度得到提升.文献[9]用fp-tree的首元对数据库进行分库，用分库代替原数据库进行候选项集支持数的统计，从而减少了Apriori算法扫描数据库的次数，提高了算法的挖掘速度.但是，基于fp-tree的Apriori算法减少的扫描数据量不够彻底，在支持数统计过程中仍然要扫描较多的分区数据，需要较多时间，算法的挖掘速度不够理想.

为了提高基于fp-tree的Apriori算法的挖掘速度，本文提出了一种改进的基于fp-tree的Apriori算法.本文的改进算法从减少扫描数据的量的角度出发，通过尾元分区、动态删除冗余数据、快速统计支持数等措施改进，进一步提高了挖掘速度.

1　Apriori算法和fp-tree结构

1.1　Apriori算法

Apriori算法为布尔关联规则挖掘频繁项集的原创性算法，使用一种称为逐层搜索的迭代思想，其中k项集用于探索k+1项集.Apriori算法主要包含以下3个步骤[10]：

候选项集生成：随机取两个频繁k项集，把当中的各个项按照顺序排列，如p={ti1，ti2，…，tik}，q={tj1，tj2，…，tjk}，满足ti1=tj1，ti2=tj2，…，tik-1=tjk-1，且tik≠tjk时，连接p、q生成候选k+1项候选项集为{ti1，ti2，…，tik，tjk}.

候选项集剪枝：剪枝则是利用了频繁项集的反单调性，设有候选k+1项候选项集包含任意非频繁项或项集，则可直接判定其非频繁项集，否则需要对数据库遍历进行支持数统计，进一步验证其是否频繁.

支持数统计：扫描数据集，累加k+1项候选项集在数据集中出现的次数.最后根据给定的最小支持数阀值生成k+1项频繁项集.在支持数计算判定频繁项集过程中存在一个定理：

定理1如果数据库中某条事务的长度为k，那么这条事务就不可能包含任何项数大于k的频繁项集

推论1若某条事务的长度小于k+1，则在k+1项候选项集的支持数统计中可以忽略此条事务数据

在Apriori算法的支持数计数步骤，因其需要扫描一遍完整的原数据集来统计支持数，在数据库事务数量较多的情况下，算法的挖掘速度会下降.

1.2　fp-tree结构

fp-tree结构是对数据进行压缩的一种树形数据结构，最早出现在FP-growth算法中.fp-tree中每个节点对应一个项元，每个节点由4个域组成：项元标识item-name，经过该节点的支持数count，项元链node-link以及父节点指针parent.另外，为了方便对树进行操作，还有一个头表HeaderTable，头表中的记录有2个域：项元标识item-name、项元链链头node-head，其中node-head指向fp-tree中首次创建某一项元的节点.fp-tree中实线是父节点指针，虚线是项元链.fp-tree相关概念及结构细节详见文献[11].图1显示了fp-tree在表1样例数据集上的结构.

表1　样例数据集

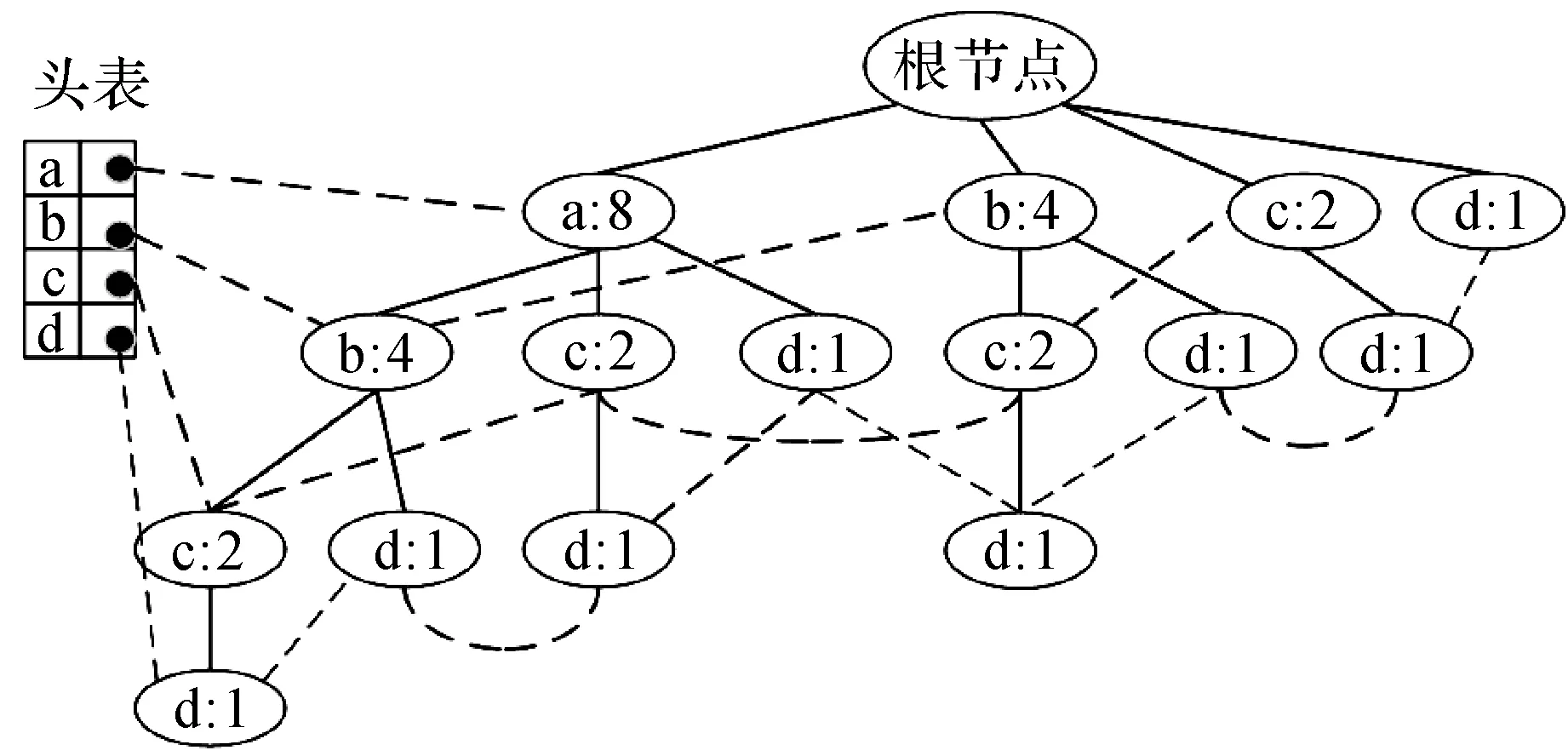
图1　fp-tree结构Figure 1　fp-tree Structure

2　改进算法

2.1　算法的改进思想

为了提高基于fp-tree的Apriori算法的挖掘速度，从进一步缩减扫描数据量的改进方向进行研究，本文通过以下几个方法进行改进和优化：其一，改变算法的分区方法，使用尾元分区的方式进行分区，可以得到数据量更小的子数据集.第二，依据Apriori算法的性质，动态删减子数据集中小于当前迭代维度数的冗余数据，数据动态缩减使得子数据集的数据进一步得到缩减.最后，通过扫描子数据集进行快速统计，迅速统计候选项集的支持数，并判断此候选项集是否是频繁项集，从而快速挖掘.具体的改进方法如下：

尾元分区：通过候选项集的尾元搜索fp-tree，将原数据集划分生成若干子数据集，从而达到缩减数据量的目的.生成的每一个子数据集在内存中仅有一份，生成后无须再度生成.尾元分区的具体过程如下：

图2tk对应的fp-tree分枝
Figure 2Corresponding fp-tree Branch

若候选项集中存在某尾部项元tk，则tk的子数据集生成过程如下：找到项元tk在头表HeaderTable中的项元链链头node-head，通过node-head找到在fp-tree中项元标识item-name为tk的第一个节点tk1.假设节点tk1所在fp-tree前缀分枝的普遍形式如图2所示，则通过遍历分枝可以得到分枝上所有节点的信息，获取分枝上每个节点的item-name汇总成向量表示形式，得到分枝向量的一般表示形式为

k=[t1t2…tk].

(1)

可得tk1分枝向量为k1，并记录tk1节点的支持数count为S1.通过tk1节点的项元链node-link找到下一个位置的tk节点tk2，并以同样的方式生成tk2节点所在分枝的向量k2，并记录支持数为S2.根据当前节点的node-link遍历下一个节点，直至到最后一个节点tki，可得分枝向量ki，支持数Si，至此停止遍历.将所有的分枝向量汇总，可得到此项元tk的子数据集为

Mk={k1,k2,…,ki}.

(2)

对应的支持数数据集为

Sk={S1,S2,…,Si}.

(3)

其中Sk数据集记录了子数据集中的每一条分枝对应的支持数，用于下文的快速支持数统计.

通过尾元分区，将具有相同尾元的频繁项集所要扫描的数据归为同一子数据集，从而避免了对无关数据的扫描，在含有大量频繁项集的情况下，数据得到缩减的量较多，算法挖掘速度提升也较多.

数据动态缩减：候选项集的迭代生成是从低维向高维进行递推.根据定理1和推论1可知，当事务数小于迭代的维度数时，可知在此事务中肯定不包含当前维度数的频繁项集.那么，在支持数统计中可以忽略此事务，将此事务从子数据集删除，从而达到缩减扫描数据量的目的.子数据集数据动态缩减的描述如下：

在子数据集已经生成的基础上，若要统计某候选项集Ck=[t1t2…tk]的支持数，则选取Ck最尾部的项元tk，找到tk所对应的子数据集，如式(2)子数据集Mk.其中，若当前迭代的维度为j，则删除Mk中事务数小于j的事务，得到数据量更小的新Mk.

数据动态缩减的改进方法是在上一层经过缩减的子数据集的基础上进行缩减，在当迭代的维度数越高时，可以删减的冗余数据也越多，从而对算法的挖掘速度的提升越明显.

快速统计支持数：遍历新Mk，将其中每一个分枝的向量与Ck进行比较，若ki包含Ck，则认为此分枝包含候选项集Ck，累加式(3)支持数数据集Sk中对应此分枝的支持数，若有整数n个分枝包含候选项集Ck，则最终候选项集Ck的支持数有

(4)

若S大于最小支持数，则候选项集Ck是频繁项集.

本文提出的改进算法通过以上思路和方法进行改进，提高了算法挖掘速度，尤其是对含有大量高维度数频繁项集的数据集，扫描数据的量会得到大幅缩减，算法挖掘速度可以得到明显提升.

2.2　算法描述

在Apriori候选项集生成机制上，算法主要增加了使用fp-tree的步骤：通过尾元划分数据，并在生成和使用子数据集的过程中只选取大于等于当前迭代维度数的事务，即动态缩减数据，最后通过候选项集和子数据集的比较进行支持数快速统计，判断是否是频繁项集.

使用fp-tree的伪代码如下：

输入：候选项集Ck、fp-tree、最小支持数min_support

输出：频繁项集Lk

1)begin

2)for each candidate candiItem∈Ck

3)support=0

//将候选项集转换成向量

4)canMatrix:=candiItem trans to matrix and sort

//获得尾元进行分区，得到子数据集

5)oneItem=canMatrix[max]

//得到fp-tree的第一个节点

6)currNode=HeaderTable[oneItem]

//遍历所有节点

7)while currNode.hasNext

8)currNode=currNode.next

//将当前节点的fp-tree分枝转换成向量

9)tempMatrix:=Get prefix and trans to matrix

//数据动态缩减，剔除小于当前维度数的事务

10)if tempMatrix.size>=candiItem.size

11)add tempMatrix to Matrix[oneItem]

12)end if

//快速统计支持数

//若分枝包含候选项集则累加支持数

13)if canMatrix∩tempMatrix equals canMatrix

14)support+=currNode.support

15)end if

16)end while

//判断是否是频繁项集

17)if support>min_support

18)add candiItem to Lk

19)end if

20)cache the Matrix

21)end for

22)end

3　实验分析

实验是在CPU为I5 4590，8 G内存的硬件环境下，操作系统为Windows，编程语言为Java，编辑工具为Eclipse的软件环境下完成实验数据的获取和测量，并使用Matlab展示实验图表.实验使用经典的关联规则算法数据集T10I4D100K和Accidents，均是从FIMI存储库(http://fimi.ua.ac.be/data/)下载.本文分别在这两种数据集上进行对比试验，每组试验的参数都是不变的，都是通过改变最小支持度从而记录算法的运行时间，算法运行的时间越小代表算法的挖掘速度越快.

实验一图3的实验采用了T10I4D100K数据集，该数据集是个数据量为100 000的人工数据集，在最小支持度大于5%，频繁项集较少，此时，改进算法得到的提升不高.在最小支持度小于5%时，会出现大量的频繁项集，由于本文尾元分区的改进方法减少了统计频繁项集支持数所需扫描数据的量，从而对于这些大量的频繁项集进行扫描时间也会相应地减少，尤其当最小支持度为4%时.本文改进算法的运行时间较文献[8]缩短了61.7%，较文献[9]缩短了72.6%.可见对于含有大量频繁项集的数据集，本文改进算法挖掘的速度较高.

实验二图4的实验采用了Accidents数据集，该数据集的平均事务长度和频繁项集的长度都会较长，说明在逐层迭代过程中会对维度数较高的候选项集进行支持数统计；而根据本文改进算法动态缩减数据的改进方法，对维度数越高的频繁项集进行支持数统计，那么减少的扫描数据的量也越多，从而缩减的运行时间也越多，算法的挖掘速度也越快.从图4的实验结果上可知，在最小支持度为60%时，本文改进算法的运行时间较文献[9]缩短了76%，较文献[8]缩短了70%.

图3　T10I4D100K上运行时间对比Figure 3　Running time comparisonon T10I4D100K

图4　Accidents上运行时间对比Figure 4　Running time comparison on Accidents

综合实验分析可知，当数据集在一定最小支持度区间内出现大量频繁项集和频繁项集维度数较高时，本文改进算法的挖掘速度要快于文献[9]算法和文献[8]算法.可见，本文提出的改进的基于fp-tree的Apriori算法的挖掘速度得到提升.

4　结　语

本文提出改进的基于fp-tree的Apriori算法，从缩减扫描数据量的角度出发，采用改变分区方式、缩减冗余数据量和快速支持数扫描等措施提升算法挖掘速度，通过实验验证了改进算法的挖掘速度得到提高.

【参考文献】

[1]崔贯勋,李梁,王柯柯.关联规则挖掘中Apriori算法的研究与改进[J].计算机应用,2010,30(11)：2952-2955.

CUI G X, LI L, WANG K K.Research and improvement on apriori algorithm of association rule mining[J].JournalofComputerApplications, 2010,30(11)：2952-2955.

[2]罗丹,李陶深.一种基于压缩矩阵的Apriori算法改进研究[J].计算机科学,2013,40(12)：75-80.

LUO D, LI T S.Research on improved apriori algorithm based on compressed matrix[J].ComputerScience, 2013,40(12)：75-80.

[3]PARK J S, CHEN M S, YU P S.An effective hash-based algorithms for mining association rules[C]//Proceedingsofthe1995ACMSIGMODInternationalConferenceonManagementofData. California：ACM Press,1995：175-186.

[4]AGRAWAL R, SRIKAN R. Fast algorithms for mining association rules in lager databases[C]//ProceedingsoftheTwentiethInternationalConferenceonVeryLargeDatabases.Santiago：IEEE,1994：487-499.

[5]JIA W H, JIAN P, YIN Y W, et al.Mining frequent patterns without candidate generation：A frequent patterns tree approach[J].DataMiningandKnowledgeDiscovery, 2004,8(1):53-87.

[6]肖继海,崔晓红,陈俊杰.基于cofi-tree的N-最有兴趣项目集挖掘算法[J].计算机技术与发展,2012,35(2)：99-102.

XIAO J H, CUI X H, CHEN J J.Mining n-most interesting itemsets algorithm based on cofi-tree[J].ComputerTechnologyandDevelopment,2012,22(3)：99-102.

[7]YUDHOG S, RAJ P G. CT-PRO：A bottom-up non frequent itemset mining algorithm using compressed fp-Tree data structure[C]//ProceedingsoftheIEEEICDMWorkshoponFrequentItemsetMiningImplementations. Brighton：IEEE, 2004：212-223.

[8]吴倩,罗健旭.压缩FP-Tree的改进搜索算法[J].计算机工程与设计,2015,36(7)：1771-1777.

WU Q, LUO J X. Improved search algorithm based on compressed fp-tree[J].ComputerEngineeringandDesign, 2015,36(7)：1771-1777.

[9]张宁.基于fp-tree的Apriori算法的改进[J].信息通信,2015,2：94-95.

ZHANG N. Improvement of apriori algorithm based on fp-tree[J].Information&Communications, 2015,2：1771-1777.

[10]钱光超,贾瑞玉,张然.Apriori算法的一种优化方法[J].计算机工程,2008,34(23)：196-198.

QIAN G C, JIA R Y, ZHANG R.One optimized method of apriori algorithm[J].ComputerEngineering, 2008,34(23)：196-198.

[11]赵强利,蒋艳凰,徐明.基于fp-tree的快速选择性集成算法[J].软件学报,2011,22(4)：709-721.

ZHAO Q L, JIANG Y H, XU M.Fast ensemble pruning algorithm based on fp-tree[J].Journalofsoftware, 2011,22(4)：709-721.