路与圈笛卡尔乘积图的误报容错支配数

李红丽，赵承业

(中国计量大学 理学院，浙江 杭州 310018)

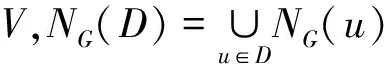
图的误报容错支配集可以在监测节点发出错误信息的时候仍然能够定位事故发生节点，并识别发出错误信息的节点，因此在网络容错设计中具有很重要的价值[3-5].

关于图的误报容错支配数已经有了很多结论[6-9],2009年,Slater[2]引入了误报容错支配的概念并且给出了误报容错支配数的一个下界,即如果对于一个图G(顶点数n=|V(G)|)它的最大度ΔG=r,特别的,如果图G是r正则图,则它的最小误报容错支配数γLR(G)≥(6/(3r+2))n.2012年王浩丽[10]给出了广义Petersen图P(n,1),P(n,2)的误报容错支配数的值.2013年,裴利丹[11]等确定了γ(Pm×Cn)的值.其中m=3,4.目前针对路与圈笛卡尔乘积图误报容错支配还没有研究,本文主要讨论Pm×Cn(m=3,4)的误报容错支配数.

1　引理及主要结果

首先给出几个记号.

在图Pm×Cn中,令V′(i,t)={v0(i+j),v1(i+j),…,v(m-1)(i+j)：0≤j≤t}是Pm×Cn的一个子集,其中0≤i≤n-1且0≤t≤n.显然,

令L是Pm×Cn中任意一个误报容错支配集,且令ni,t代表顶点子集V′(i,t)∩L中的顶点数目,即ni,t=|V′(i,t)∩L|.

引理1当n≥5时,

γLR(P3×Cn)≤.

证明:要证明该引理，只需找出一个满足该引理条件的误报容错支配集L.

当n=5时,令

L={v10,v01,v11,v21,v03,v13,v23,v14}.

当n=6时,令

L={v01,v11,v21,v03,v13,v23,v05,v15,v25}.

当n≥6时,令

S={v0(2i+1),v1(2i+1),v2(2i+1)：0≤i≤k-1}

且

(1)

不难验证L是图P3×Cn的满足引理条件的误报容错支配集.

由于P3×Cn中每个顶点必须被支配两次，因此以下观察成立.即

观察1对任意i∈{0,1,…,n-1},

ni,1≥2.

引理2对任意i∈{0,1,…,n-1},有ni,2≥3,如果存在一整数l∈{0,1,…,n-1},满足nl,2=3,则{v0(l+1),v1(l+1),v2(l+1)}⊂L且nl+1,2=6.

证明:由观察1容易得出对任意i∈{0,1,…,n-1}有ni,2≥3.现假设存在一个整数l∈{0,1,…,n-1},使得nl,2=3,由观察1,我们考虑以下两种情形:

情形1nl,1=2,nl+2,0=1.

为支配V′(l,2)中每个顶点两次,我们分以下两种情形考虑:

1)nl,0=0,nl+1,0=2,nl+2,0=1时,V′(l,0)中存在一个顶点至多被支配一次,这与每个顶点必须被支配两次矛盾,因此此情形不成立.

2)nl,0=nl+1,0=nl+2,0=1时,V′(l+1,0)中至少存在一点至多被支配一次，矛盾.

情形2nl,1=3,nl+2,0=0.

为支配V′(l,2)中每个顶点两次,考虑两种情形:

1)nl,0=1,nl+1,0=2,nl+2,0=0时,V′(l+2，0)中存在一点至多被支配一次，矛盾.

2)nl,0=0,nl+1,0=3,nl+2,0=0时,{v0(l+1),v1(l+1),v2(l+1)}⊂L,则V′(l+1,0)中的每一个顶点被支配两次,且对任意的一对u,v∈V′(l+1,0),|(N[u]∪N[v])∩L|=3成立.又由于{v0(l+2),v1(l+2),v2(l+2)}⊄L,为支配V′(l+2,0)中每个顶点两次,{v0(l+3),v1(l+3),v2(l+3)}⊂L.则nl+1,2=6成立,且在V′(l+2,0)满足对任意一对顶点u,v∈V′(l+2,0),|(N[u]∪N[v])∩L|≥3.

引理3对任意n≥5，

γLR(P3×Cn)≥.

证明:我们考虑以下两种情况:

通过情形1和情形2,证得引理3.

根据引理1和引理3,得到如下定理:

定理1对任意的n≥5,有

γLR(P3×Cn)=.

引理4对任意n≥5,

证明:要证明该引理,只需给出一个满足该引理条件的误报容错支配集L.

当n=5时,令

L={v00,v30,v01,v11,v21,v31,v03,v13,v23,v33,v24}.

当n=6时,令

L={v01,v11,v21,v31,v03,v13,v23,v33,v05,v15,v25,v35}.

当n≥6时,令

S={v0(2i+1),v1(2i+1),v2(2i+1),v3(2i+1)：0≤i≤k-1}

且

(2)

不难验证L是图P4×Cn的满足引理条件的误报容错支配集.

观察2对任意i∈{0,1,…,n-1},

ni,1≥3.

引理5对任意i∈{0,1,…,n-1},有ni,2≥4.如果存在一个整数l∈{0,1,…,n-1},满足nl,2=4,则{v0(l+1),v1(l+1),v2(l+1),v3(l+1)}⊂L,nl+1,2=8.

证明:由观察2不难得出i∈{0,1,…,n-1},使得ni,2≥4.现假设存在一个整数l,满足nl,2=4,对任意l∈{0,1,…,n-1}.由观察2,我们考虑以下两种情况:

情形1nl,1=3,nl+2,0=1.

为支配V′(l,2)中每个顶点两次,我们分以下两种情形考虑:

1)nl,0=1,nl+1,0=2,nl+2,0=1时,V′(l，0)和V′(l+2,0)中存在一个顶点至多被支配一次,这与每个顶点必须被支配两次矛盾,因此此情形不成立.

2)nl,0=0,nl+1,0=3,nl+2,0=1时,则V′(l,0)中存在一个顶点至多被支配一次,矛盾.

情形2nl,1=4,nl+2,0=0.

为支配V′(l,2)中每个顶点两次,分以下两种情形考虑:

1)nl,0=1,nl+1,0=3,nl+2,0=0时,V′(l+2,0)中存在一个顶点至多被支配一次，矛盾.

2)nl,0=0,nl+1,0=4,nl+2,0=0时,{v0(l+1),v1(l+1),v2(l+1),v3(l+1)}⊂L,则V′(l+1,0)中的每一个顶点都被支配两次,且对任意的一对顶点u,v∈V′(l+1,0),|(N[u]∪N[v])∩L|≥3成立.又由于{v0(l+2),v1(l+2),v2(l+2),v3(l+2)}⊄L为支配V′(l+2,0)中每个顶点两次,{v0(l+3),v1(l+3),v2(l+3),v3(l+3)}⊂L.则nl+1,2=8成立,且对任意的一对顶点u,v∈V′(l+2,0),|(N[u]∪N[v])∩L|≥3.

引理6对任意n≥5,有

证明:考虑以下两种情形:

情形1当n为偶数时,由引理5,假设ni,2=4,对任意的i∈{0,1,…,n-1},则有{v0(i+1),v1(i+1),v2(i+1),v3(i+1)}⊂L,ni+1,2=8.由图的对称性,图P4×Cn的误报容错支配集的顶点数至少为2n,即γLR(P4×Cn)≥2n.

情形2当n为奇数时,如同情形1,假设ni,2=4,对任意的i∈{0,1,…,n-1},则有{v0(i+1),v1(i+1),v2(i+1),v3(i+1)}⊂L,ni+1,2=8.由对称性,可知{v0(i+3),v1(i+3),v2(i+3),v3(i+3)}⊂L,{v0(i+5),v1(i+5),v2(i+5),v3(i+5)}⊂L，等依次类推.因为n为奇数,由图的性质,存在一个整数l,使得nl,1=0对任意的l∈{0,1,…,n-1},为使V′(l,1)中的每一个顶点被L支配两次,由观察1,nl,1≥3.综上,当n为奇数时图P4×Cn的误报容错支配集的顶点数至少为2n+1,即γLR(P4×Cn)≥2n+1.

通过情形1和情形2,证得引理6.

根据引理4和引理6,得到如下定理:

定理2对任意的n≥5,有

2　m大于4的猜想

通过观察图Pm×Cn(m=3,4)的误报容错支配数的精确值，我们可以发现它和m,n的关系大致满足.对m大于4的情形,我们猜想存

在非负整数c,d,对任意的m,n有下面的结论成立:

+d.

【参考文献】

[1]HARAY F, HAYNES T W. Double domination in graphs[J].ArsCombin, 2000,55:201-213.

[2]SLATER P J. Liar’s domination[J].Network, 2009,54(2):70-74.

[3]RODEN, MIRANDA L, SLATER, et al. Liar’s domination in graphs[J].DiscreteMathematics, 2009,309(19):5884-5890.

[4]ALIMADADI A, CHELLALI M, MOJDEH D A. Liar's dominating sets in graphs[J].DiscreteAppliedMathematics, 2016,211:204-210.

[5]张超,赵承业.计算树的[1,2]-数的算法研究[J].中国计量学院学报,2015,26(2):243-246.

ZHANG C, ZHAO C Y. Research on the algorithms of computing the[1,2]-number of trees[J].JournalofChinaUniversityofMetrology,2015,26(2):243-246.

[6]ALIMADADI A, MOJDEH D A, RAD N J. Various bounds for liar’s domination number[J].DiscussionesMathematicaeGraphTheory,2016,36(3):629-641.

[7]PANDA B S, PAUL S. Liar’s domination in graphs: Complexity and algorithm[J].DiscreteAppliedMathematics, 2013,161:1085-1092.

[8]PANDA B S, PAUL S. A linear time algorithm for liar’s domination problem in proper interval graphs[J].InformationProcessingLetters, 2013,113:815-822.

[9]PANDA B S, PAUL S, PRADHAN D. Hardness results, approximation and exact algorithms for liar's domination problem in graphs[J].TheoreticalComputerScience,2015,573:26-42.

[10]王浩丽.图的支配数及两个相关问题的研究[D].大连：大连理工大学,2011.

WANG H L.ResearchonDominationNumberandTwoRelatedProblemsofGraphs[D].Dalian: Dalian University of Technology,2011.

[11]裴利丹,连小娟,潘向峰.路与圈的笛卡尔乘积的控制数[J].合肥学院学报(自然科学版),2013,23(3):24-28.

PEI L D,LIAN X J,PAN X F.On the domination number of the cartesian products of the cycle and the path[J].JournalofHefeiUniversity(NaturalSciences),2013,23(3):24-28.