基于博弈论的社交网络转发控制机制

2018-04-19单芳芳李晖朱辉

通信学报 2018年3期

单芳芳，李晖，朱辉

基于博弈论的社交网络转发控制机制

单芳芳1,2，李晖1,3，朱辉1,3

（1. 西安电子科技大学网络与信息安全学院，陕西西安 710071；2. 中原工学院计算机学院，河南郑州 450007；3. 综合业务网理论与关键技术国家重点实验室，陕西西安 710071）

随着移动通信和互联网技术的快速发展，社交网络逐渐成为人们开展社交活动的主流方式之一。为了维护并增强人际关系，用户乐于在社交网络中分享个人行为、心情等内容，但对这些内容的转发操作会为发布者带来隐私泄露的风险。为解决社交网络中的转发决策问题，在分析转发双方收益的基础上，提出一种基于博弈论的社交网络转发控制机制，能够有效阻止转发者的非诚信转发行为。在分析转发者与发布者选择不同博弈策略所得收益的基础上，结合转发操作的历史数据，计算转发者进行非诚信转发的概率，并通过与发布者设置的阈值进行比较，给出是否允许转发的最终决定。介绍了基于博弈论的转发控制流程及架构设计，对博弈双方收益进行定义和分析，给出博弈过程，通过实验验证所提机制能够支持发布者给出最佳转发决策，保障发布者的内容安全。

社交网络；转发控制；博弈论；纳什均衡

1 引言

在飞速发展的通信技术和互联网技术的推动下，社交网络逐渐融入人们的工作、学习和生活。越来越多的用户通过社交网络分享日志、开展日常社交活动。面对日益增长和多样化的在线社交需求，各具特色的社交网络也应运而生，如国外的Facebook、Twitter以及面向商业客户的LinkedIn，国内的QQ、微信、新浪微博等[1]。此外，一些电商、支付类软件也加入社交功能，如京东、支付宝等。这些社交网络可以帮助用户查找兴趣相近的朋友，与好友分享文字、图片或视频等信息，了解身边好友的近况。方便、快捷的特征为社交网络带来了大量的用户。据统计，2015年Facebook平均每天在线的用户数目多达9 680万，而每月活跃用户数目则有14.9亿[2]。

社交网络在方便用户分享信息的同时，不可避免地带来了用户隐私泄露问题。多数社交网站采用权限管理功能保护用户隐私。例如，Facebook允许用户设置发布的内容为“朋友可见”，或“朋友的朋友可见”；Twitter允许用户设置个性化的访问控制方案，同时支持禁止浏览器保存Cookie的选项[3]；QQ空间允许用户将日志设置为“公开”“QQ好友可见”“指定好友可见”或“仅自己可见”；微信朋友圈允许用户设置展示3天或半年的朋友圈信息，在朋友圈发布图片或视频信息时，用户可选择“公开”“私密”“部分可见”或“不给谁看”。

目前，学术界针对社交网络隐私保护问题的研究集中在访问控制技术[4]。基于对Web2.0应用程序安全需求的分析，Gates[5]提出第一个基于关系的访问控制机制，以保护网络中的内容安全。文献[6]提出的访问控制模型首次考虑信任等级、关系深度以及关系类型等因素，并将其用于访问控制授权决策。在文献[7]中，研究者们考虑采用语义网技术解决社交网络中内容的访问控制问题。Fong等[8]对Facebook社交网络进行深入研究，提出针对实际社交网络的访问控制机制。文献[9]将模态逻辑语言用于社交网络中访问控制策略的定义。随后，Fong等[10]对模态逻辑进行扩展以支持访问控制策略中共同好友的描述。为了提高访问控制授权效率和策略的表达能力，Bruns等[11]利用混合逻辑对文献[10]进行扩展，提出基于混合逻辑的访问控制模型。Park等[12]将正则表达式作为策略语言，用于策略的定义，提出一种利用用户之间关系实施访问控制的模型UURAC。随后，Park等[13]对UURAC进行扩展以支持用户—资源关系以及资源—资源关系，并在后续的研究中进一步支持访问控制策略冲突的消解[14]。文献[15,16]分别将密码协议和属性加密等密码技术用于控制网络中内容的访问，为社交网络访问控制技术指出了新的发展方向。

社交网络是一个虚拟化的环境，添加陌生人为好友，用户面临个人隐私内容被恶意访问的风险。针对该问题，研究者引入博弈论，用于解决社交网络中所发布个人内容的安全问题。文献[17]利用博弈论分析社交网络中内容访问者和内容发布者的收益，提出一种新的访问控制机制。文献[18]提出一种博弈控制机制，该机制采用博弈论对社交网络中用户的行为进行分析，并通过用户行为信任预测来控制社交网络中资源的访问。Yu等[19]为社交网络中的竞争信息传播建立一个博弈模型，用于理解知识、兴趣、金钱以及学习欲望等人类行为对竞争信息传播的影响。文献[20]利用博弈论计算资源访问者和资源发布者的收益得到纳什均衡，并据此决定是否允许访问资源。文献[21]将重复博弈和激励机制用于提高社交网络中资源共享的效率。张伊璇等[22]从社交网络内容访问双方收益的角度出发，在考虑历史访问数据对当前收益影响的基础上，利用博弈理论保护社交网络中用户的隐私信息。

已有的基于关系和利用博弈论实现的访问控制方法仅针对社交网络中资源的访问操作进行约束，并未对转发操作实施控制。然而，得到资源的访问授权后，访问者可能对内容进行恶意转发。例如，发布者关于热点事件发表精彩评论，转发者为了提高个人影响力而不加出处转发，或转发时将其据为己有；发布者发布包含隐私信息的个人照片并设置访问范围，获得访问权的用户转发照片并将其公布于发布者设置的访问范围以外。上述转发操作会对发布者带来不利影响，甚至泄露个人隐私。因此，对转发者的转发请求做出恰当的转发决策对于发布者至关重要。

本文运用博弈论对转发授权决策问题进行研究，提出了一种基于博弈论的社交网络转发控制机制。首先，定义并分析了转发者与发布者选择不同博弈策略所得收益，得到内容转发双方的收益矩阵，结合转发操作的历史数据计算转发者进行非诚信转发的概率。然后，通过与发布者设置的阈值进行比较，给出是否允许转发的最终决定，并通过实验验证所提机制能够支持发布者给出最佳转发决策，保障发布者的内容安全。本文假设参与博弈的转发者和发布者是理性的，转发者与发布者的决策有先后之分，然而，后续决策的发布者无法观察到转发者所采取的策略，等同于博弈双方同时决策，故本文所描述的博弈是静态博弈。

2 收益矩阵的定义及分析

本文所述博弈双方分别是内容的发布者和转发者。发布者可采取的策略分别为“同意转发”或“拒绝转发”。转发者可采取的策略分别为“诚信转发”或“非诚信转发”。“诚信转发”指转发者能够按照发布者的要求设置转发内容的访问控制策略并声明所转发内容的所有权属于发布者，“非诚信转发”指转发者违背发布者的要求随意扩散转发内容，或利用技术手段将转发内容据为己有。

博弈双方的收益定义如下。

表示转发者实施“诚信转发”策略，发布者实施“同意转发”策略时，发布者的收益。该收益可表现为收获新的好友、得到更多关注、增加内容访问量、扩大社交影响力等。

表示转发者实施“诚信转发”策略，发布者实施“拒绝转发”策略时，发布者的损失。该损失可表现为错过新的好友及失去潜在内容访问量等由于社交资源未充分利用而失去的机会。

表示转发者实施“非诚信转发”策略，发布者实施“同意转发”策略时，发布者的损失。该损失可表现为隐私信息被不可控传播、知识产权被侵犯等。

表示转发者实施“诚信转发”策略，发布者实施“同意转发”策略时，转发者的收益。该收益可表现为扩大社交影响力、提高社交活跃度、获得与对转发内容感兴趣的相关用户加深交流的机会等。

表示转发者实施“诚信转发”策略，发布者实施“拒绝转发”策略时，转发者的损失。该损失可表现为失去扩大社交影响力的机会等。

表示转发者实施“非诚信转发”策略，发布者实施“同意转发”策略时，转发者获得的额外收益。该收益可表现为转发者将内容转发给没有访问权限的用户并收取相关费用，或将内容据为己有，发布后提升社交影响力等。

表示转发者实施“非诚信转发”策略后可能受到的处罚。例如，拒绝访问隐私信息、追究侵犯版权的法律责任等。

表示转发者实施“非诚信转发”策略的开销。如更改内容所有权、为屏蔽内容发布者的查看而付出的代价等。

当转发者和发布者分别采取“诚信转发”策略和“同意转发”策略时，发布者由于内容广泛扩散得到更多关注，提高知名度和社交影响力，转发者由于转发有意义的内容而吸引更多兴趣相同的社交成员关注，好友增加，社交活跃度提高。博弈双方的收益分别表示为和。

当转发者和发布者分别采取“非诚信转发”策略和“同意转发”策略时，发布者的过度信任导致包含其隐私信息的内容在社交网络中不可控传播，其损失表示为−；转发者在获得诚信转发收益外，还得到额外收益，同时付出非诚信转发的开销及非诚信转发受到的处罚，其收益表示为−−。假设>+，即转发者非诚信转发的收益大于诚信转发的收益。

当转发者和发布者分别采取“诚信转发”策略和“拒绝转发”策略时，发布者由于合作失败而失去扩大社交影响力的机会，其损失表示为−。转发者采取“诚信转发”策略不需要付出额外成本，由于转发请求被拒绝，其收益为0。

当转发者和发布者分别采取“非诚信转发”策略和“拒绝转发”策略时，发布者由于成功保护了包含其隐私信息的内容或知识产权，获得收益表示为，其值与发布者同意转发者的非诚信转发请求的损失相等，即=。转发者采取“非诚信转发”策略被拒绝时，其收益表示为−。

表1 收益矩阵

在上述讨论的基础上做以下假设。假设>+，即转发者采取“非诚信转发”策略所得收益大于“诚信转发”所得收益。假设<，即转发者诚信转发被拒绝的损失小于转发者非诚信转发要付出的开销。

表1给出了转发者和发布者的收益矩阵。转发者针对同一个发布者所发布的不同内容的转发历史记录会对后续转发产生影响，换句话说，多次转发将提高转发者泄露发布者隐私信息的概率。因此，设置参数因子为1~9，转发控制机制将根据转发者的转发历史记录对其进行调整。

用划线法对转发者和发布者的收益矩阵进行分析。就发布者而言，如果转发者选择“诚信转发”，发布者将选择“同意转发”，因为同意转发的收益大于拒绝转发的收益，即×1> −×8；相反，如果转发者选择“非诚信转发”，发布者将会“拒绝转发”，因为拒绝转发的收益大于同意转发的收益，即×9> −×3。就转发者而言，如果发布者选择“同意转发”，转发者将选择“非诚信转发”，因为非诚信转发的收益大于诚信转发收益，即×4×5−×6−×7×2；如果发布者选择“拒绝转发”，转发者将选择“诚信转发”，因为诚信转发的收益大于非诚信转发的收益，即0>−×6。经过上述分析，本文所述博弈模型不存在纯策略纳什均衡。

3 转发控制机制的博弈分析

由于在该博弈模型中，纯策略纳什均衡不存在，本节将在计算内容转发者和发布者收益的基础上给出博弈过程，得到混合策略纳什均衡的条件，计算出转发者进行非诚信转发概率。基于博弈论的社交网络转发控制机制支持发布者针对所发布内容设置转发阈值，用于描述发布者对于转发者非诚信转发行为的容忍程度。通过比较非诚信转发概率和转发阈值的大小决定是否允许转发者的转发请求。

转发阈值是一个介于0和1.0之间的数，由发布者根据内容的敏感程度设置。转发阈值越小，内容的私密度越低，发布者希望分享该内容；转发阈值越大，内容的私密度越高，发布者希望该内容在可控的范围内扩散。表2给出转发阈值与内容的分享度及私密度之间的关系。转发阈值介于0和0.1之间的内容，其内容私密度为I度，内容分享度为IX度，该内容私密性极低，内容分享性极高，发布者希望该内容在社交网络中广泛扩散；转发阈值介于0.9和1.0之间的内容，其内容私密度为IX度，内容分享度为I度，该内容私密性极高，内容分享性极低，发布者希望该内容在社交网络中受控扩散。

表2 转发阈值与内容分享度/私密度关系

3.1 转发控制流程

图1给出了基于博弈论的转发控制流程，流程中的详细步骤如下。

1) 转发者发起转发请求，请求转发发布者所发布的内容。

2) 系统获知转发者请求转发的内容，并从转发历史记录及阈值数据库中获取该转发者已转发过的内容。

3) 系统根据步骤2)中获取的转发内容历史信息计算参数因子。

4) 根据步骤3)中所得参数因子计算此次转发操作中转发者与发布者采取不同策略时所对应的收益。

5) 模拟转发者和发布者采取不同的博弈策略。

6) 根据转发者和发布者的博弈获得混合策略纳什均衡，从该纳什均衡中得到转发者和发布者的收益期望以及执行每个博弈策略的概率。

7) 获取步骤6)中转发者选择“非诚信转发”策略的概率。

8) 系统比较步骤7)中所得概率和发布者所设转发阈值的大小。如果“非诚信转发”概率小于转发阈值，则允许转发；否则，系统将拒绝转发请求。

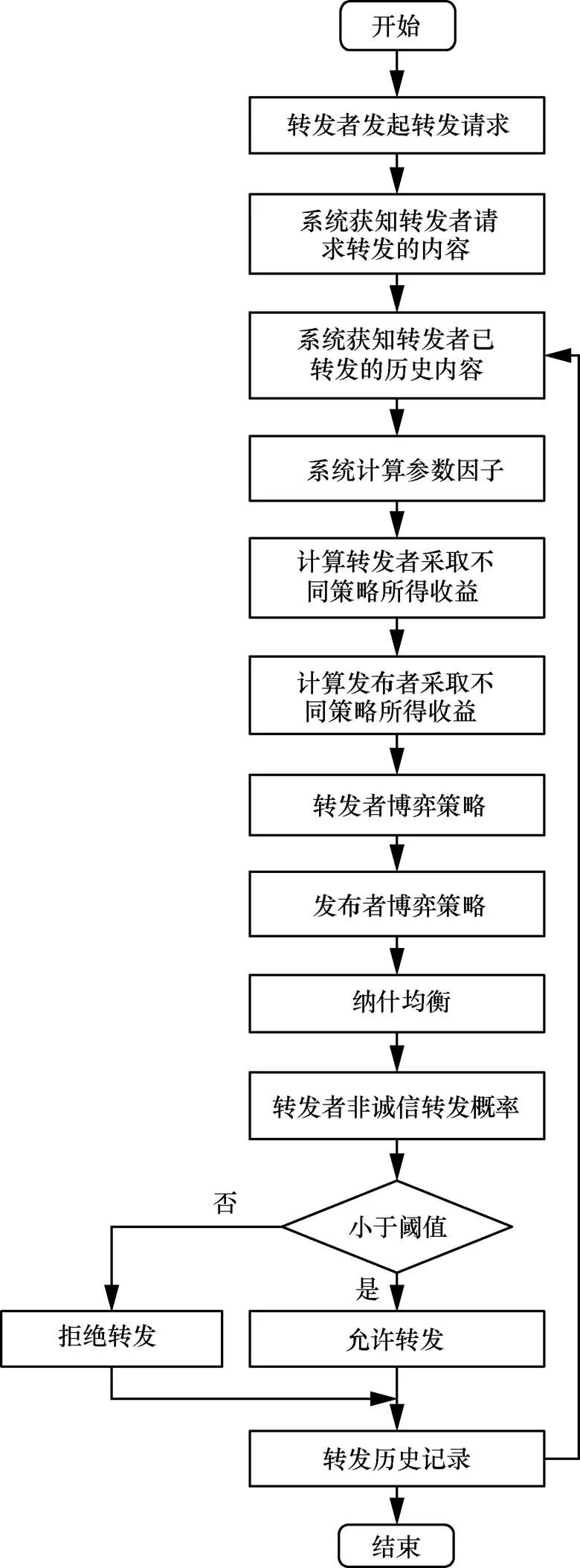
图1 基于博弈论的转发控制流程

9) 将此次转发的内容及最终结果记录到转发历史记录及阈值数据库中。当转发者再次提出转发请求时，该步骤记录的历史数据会通过步骤2)~步骤4)对博弈双方的收益产生影响，进而影响发布者决定采取“允许转发”策略或“拒绝转发”策略。

3.2 博弈过程

由于该博弈模型不存在纯策略纳什均衡，这里对其混合策略纳什均衡进行计算。假设发布者实施“允许转发”的概率为，则其实施“拒绝转发”的概率为1−，发布者的混合策略为(,1−)。转发者实施“诚信转发”的概率是，则其实施“非诚信转发”的概率是1−，转发者的混合策略为= (, 1−)。将发布者和转发者的收益矩阵分别记作和，发布者的收益函数定义为

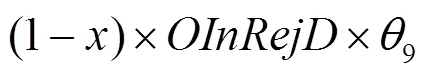
对式(1)求关于的偏导可得

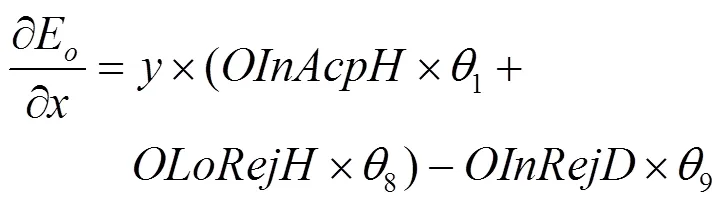
同样，转发者的收益函数定义为

对式(4)求关于的偏导可得

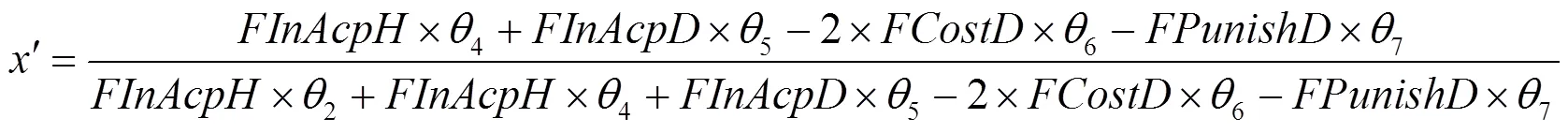
由上述分析可得混合策略纳什均衡为

其中，和的值分别如式(6)和式(3)所示，1−和1−的值分别为

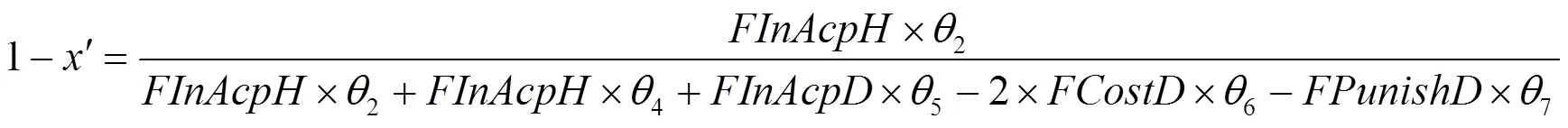
根据混合策略纳什均衡，基于博弈论的社交网络转发控制机制可以得到转发者实施“非诚信转发”策略的概率以及发布者实施“允许转发”策略的概率。当转发者提出内容转发请求，利用基于博弈论的社交网络转发控制机制比较转发阈值与转发者实施“非诚信转发”策略的概率，只有当“非诚信转发”策略的概率小于转发阈值时，才允许转发者转发所请求内容。

3.3 转发控制机制的架构设计

图2是基于博弈论的转发控制机制的架构设计。该架构设计包括执行部分、转发控制部分和转发历史记录及阈值数据库3个组成部分。执行部分负责接收转发者的转发请求并执行最终的转发控制决策，支持发布者设置转发阈值。转发控制部分通过执行相关算法得到转发控制的决策并将转发者当前转发的内容及此次转发决策记录到转发历史记录及阈值数据库。转发历史记录及阈值数据库负责记录发布者设置的转发阈值和转发控制部分提供的转发历史记录。

执行部分由接收模块、执行模块和阈值设置模块3个模块组成。接收模块获取转发者的转发请求，包括所请求的转发内容以及转发者的相关信息，并将这些信息提供给转发控制部分。转发控制部分给出的转发决策由执行模块接收和执行。阈值设置模块允许发布者设置所发布内容的转发阈值。

转发控制部分由参数因子获取模块、博弈模块、决策模块和历史记录获取模块组成。参数因子获取模块接收执行模块提供的转发请求及相关信息，并从历史记录及阈值数据库获取转发者的历史转发记录，依据上述信息计算此次转发所需的参数因子。博弈模块通过计算转发者和发布者的混合策略纳什均衡得到转发者选择“非诚信转发”策略的概率。决策模块比较“非诚信转发”概率与发布者所设置转发阈值的大小，只有当转发者采取“非诚信转发”的概率小于发布者所设置的转发阈值才允许转发，否则，系统将拒绝转发者的转发请求。历史记录获取模块获取此次转发者请求转发的内容及决策结果并将其记录在转发历史记录及阈值数据库中。

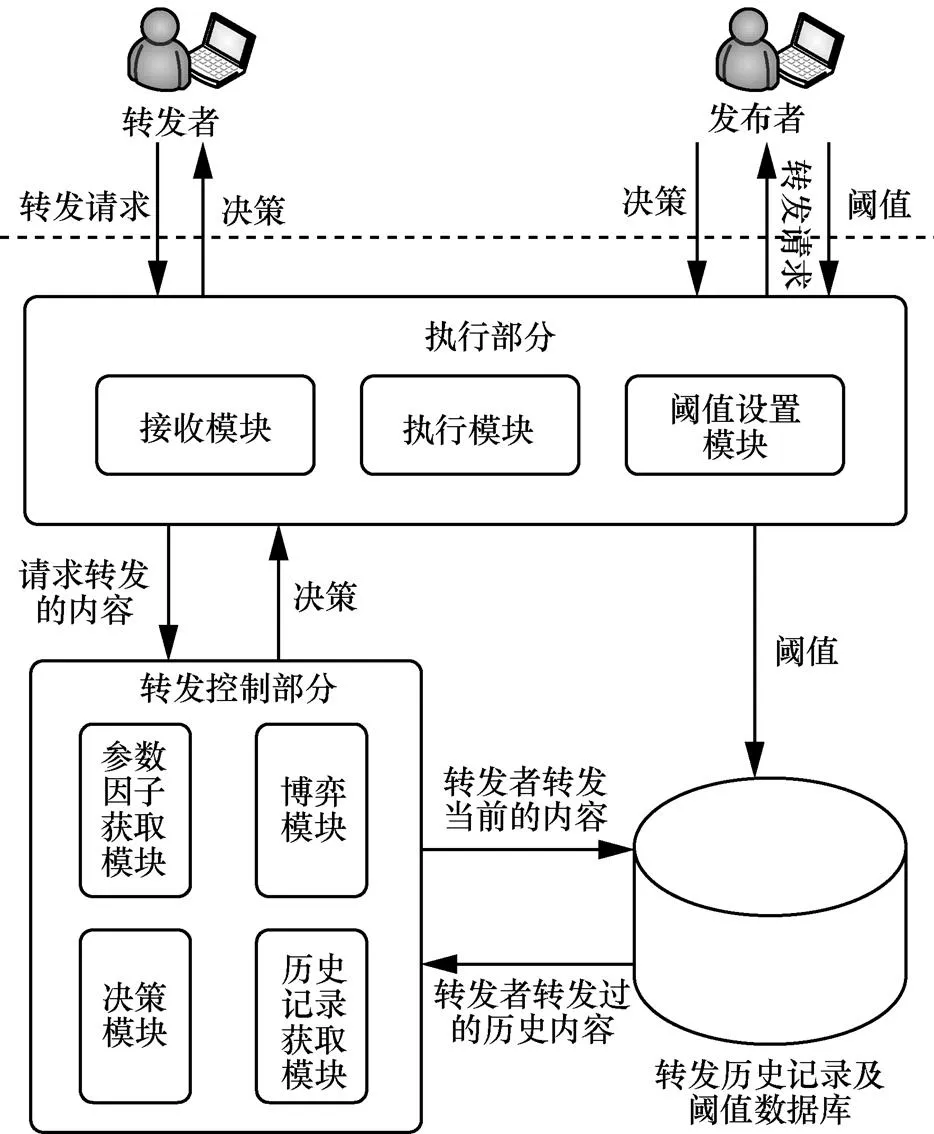
图2 基于博弈论的转发控制机制的架构设计

4 实验与算法分析

4.1 实验与分析

通过实验对本文提出的基于博弈论的社交网络转发控制机制进行分析。第一组实验考查转发者多次转发同一个发布者发布不同内容的历史信息对当前内容转发请求的影响，即转发者非诚信转发隐私内容的概率随转发次数增加的变化；第二组实验考查允许转发次数与转发阈值的关系，即随着转发阈值的变化对转发者成功转发内容次数的影响。

实验环境如下：CPU为双核i7-3770，3.4 GHz；内存为DDR 8 GB；硬盘为500 GB，7 200转；操作系统为Windows 7。仿真软件为Matlab 7.11.0（R2010b）。

为了考查转发者对同一个发布者的不同内容连续多次转发后非诚信转发概率的变化情况，本文假设系统中有一个转发者和一个发布者。发布者在社交网络中发布90个内容，其中，每10个内容共享同一个内容私密度（10个内容的转发阈值可以不同）。转发者针对每个内容私密度的内容各发起10次转发请求，考察连续10次转发者对隐私内容实施非诚信转发的概率。下面讨论相关参数的设置情况。当转发者选择“诚信转发”策略时，发布者选择“同意转发”策略获得的收益与选择“拒绝转发”策略遭受的损失相同，故设和取值同为100，同时将二者的参数因子1和8设置为相同值。考虑转发者采取“非诚信转发”策略，发布者“同意转发”时遭受的损失大于转发者诚信转发带给发布者的收益，故设的取值为180，9取值为1.0。1和8分别用于调节和的比例及历史转发记录对和的影响。私密度低的内容鼓励分享，故将I度隐私内容的1和8设置为最大值，使分享带来的收益最大化。私密度高的内容在有限范围内分享，故将IX度隐私内容的1和8设置为最小值，限制私密性高的内容分享收益。基于上述分析，将IX度隐私内容首次转发时的参数因子1和8设置为1.0，随着私密度的降低，1和8的值逐步增加。同时，转发者对同一个发布者不同内容的多次转发给转发双方带来累计收益，故参数因子随转发次数的增加呈指数级增大。IX度隐私内容在10次转发过程中取值分别为：1.00、1.01、…、1.09；VIII度隐私内容在10次转发过程中取值分别为：1.10、1.11、…、1.19；VII度隐私内容在10次转发过程中取值分别为：1.20、1.21、…、1.29；底数依次增大，直至在I度隐私内容的10次转发过程中取值达到：1.80、1.81、…、1.89。

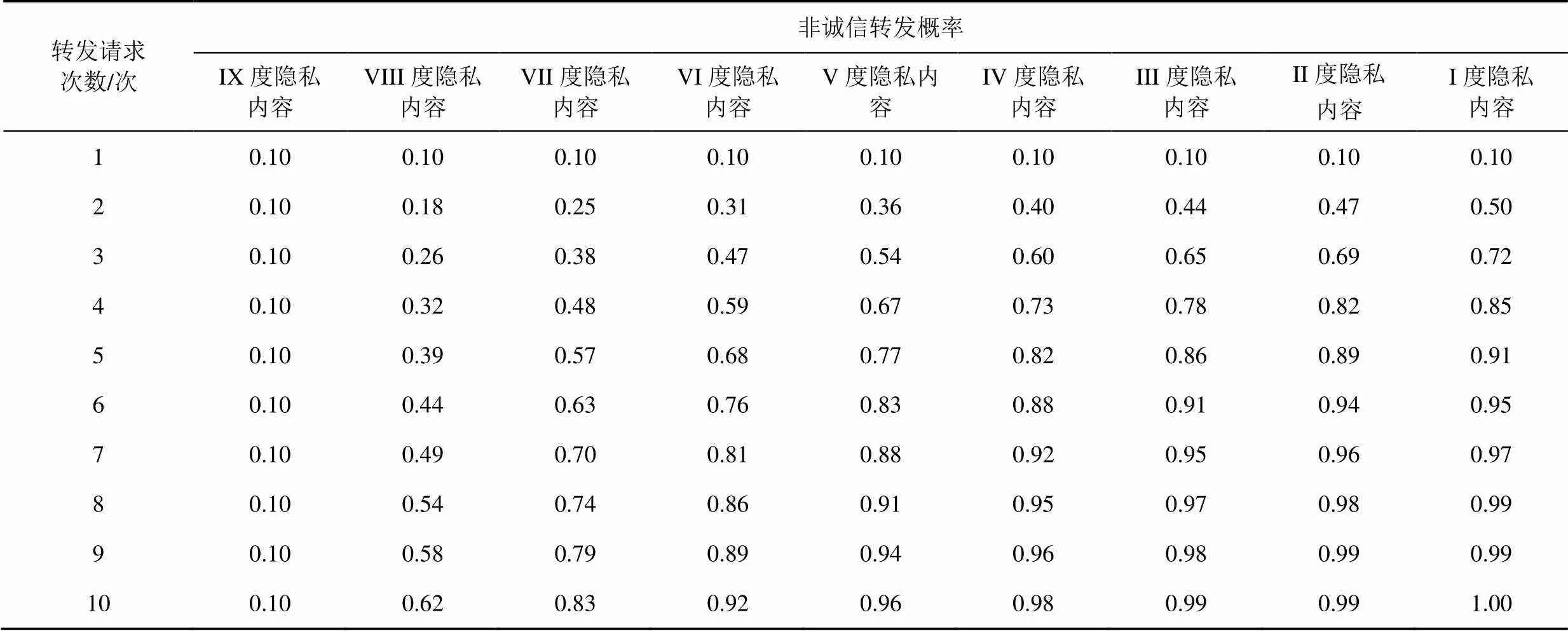
表3 非诚信转发隐私内容概率与转发请求次数的关系

表3给出了转发者非诚信转发隐私内容概率与转发请求次数之间的关系。

转发者对隐私内容进行非诚信转发的概率随着同一个私密度不同内容转发次数的增加而不断变大，说明对隐私内容的累计转发使转发者可能泄露隐私内容的概率不断增加。基于内容的私密度设置相应阈值，本文方案能够有效阻止随着转发次数增加带来的隐私泄露，保障发布者的内容安全。图3展示了上述实验的对比结果。

基于博弈论的社交网络转发控制机制允许发布者根据所发布内容的私密程度灵活设置转发阈值，用于决定是否允许转发者的转发操作。只有转发者实施“非诚信转发”策略的概率小于转发阈值时，发布者才执行“允许转发”策略。同时允许发布者根据内容的私密度设置不同的转发阈值，能够满足发布者对隐私保护的个性化需求。

图3 非诚信转发隐私内容概率

表4的结果显示，随着转发阈值的增大，转发者成功转发内容的次数在不断下降，故基于博弈论的社交网络转发控制机制能够保证发布者通过增加阈值阻止转发者非诚信转发内容，进而保障发布者的内容安全。

表4 转发阈值与转发次数的关系

4.2 算法分析

本文提出的转发控制机制根据转发次数计算参数因子时的时间复杂度为(2)，得到参数因子后计算转发者非诚信转发概率的时间复杂度为()，比较转发阈值和非诚信转发概率给出转发决策的时间复杂度为()。为了降低计算参数因子的时间复杂度，算法每次运行会保存当前参数因子。对于下一次转发请求，取出当前参数因子并乘以首次转发参数因子即可得到最新的参数因子。采取以存储空间换取运行时间的策略，可将计算参数因子的时间复杂度降低为()。由上述分析可知，本文的算法总体时间复杂度为()。

5 结束语

社交网络的发展和普及不仅给人们带来了方便，也带来了隐私泄露问题。然而，用于解决网络中内容安全的访问控制技术及隐私保护技术无法给出社交网络中转发操作的最优决策。为了解决转发操作带给内容发布者的隐私信息泄露问题，首先，分析了社交网络中内容转发双方选择不同博弈策略所得收益，并基于转发操作历史数据计算转发者实施非诚信转发策略的概率，接着，将该概率与发布者设置的转发阈值进行比较，决定是否允许转发操作，最后，通过实验验证了所提机制能够有效地帮助发布者做出最佳转发决策并保障发布者的内容安全。

下一步将根据转发阈值设置不同贴现值以完善基于博弈论的社交网络转发控制机制，并就如何保障转发者转发后的内容符合发布者的访问控制要求问题展开进一步的研究。

[1] 刘建伟, 李为宇, 孙钰. 社交网络安全问题及其解决方案[J]. 中国科学技术大学学报, 2011, 41(7): 565-575. LIU J W, LI W Y, SUN Y. Security issues and solutions on social networks[J]. Journal of University of Science &Technology of China, 2011, 41(7): 565-575.

[2] ILIA P, POLAKIS I, ATHANASOPOULOS E, et al. Face/off: preventing privacy leakage from photos in social networks[C]//ACM Sigsac Conference on Computer and Communications Security (CCS’2015). 2015: 781-792.

[3] BILTON N. Twitter implements do not track privacy option[N]. The New York Times, 2012-05-26.

[4] 姚瑞欣, 李晖, 曹进. 社交网络中的隐私保护研究综述[J]. 网络与信息安全学报, 2016, 2(4):33-43. YAO R X, LI H, CAO J. Overview of privacy preserving in social network[J]. Chinese Journal of Network and Information Security, 2016, 2(4): 33-43.

[5] GATES C E. Access control requirements for Web 2.0 security and privacy[C]//IEEE Symposium Security and Privacy (SP’07). 2007: 249-256.

[6] CARMINATI B, FERRARI E. Enforcing relationships privacy through collaborative access control in web-based social networks[C]//IEEE International Conference on Collaborative Computing: Networking, Applications and Worksharing(COLLABORATECOM’09). 2009: 1-9.

[7] CARMINATI B, FERRARI E, HEATHERLY R, et al. A semantic Web based framework for social network access control[C]//ACM Symposium on Access Control MODELS and Technologies(SACMAT’09). 2009: 177-186.

[8] FONG P W L, ANWAR M, ZHAO Z. A privacy preservation model for facebook-style social network systems[C]//European Symposium on Research in Computer Security(ESORICS’09). 2009: 303-320.

[9] FONG P W L. Relationship-based access control: protection model and policy language[C]//ACM Conference on Data and Application Security and Privacy(CODASPY’11). 2011: 191-202.

[10] FONG P W L, SIAHAAN I. Relationship-based access control policies and their policy languages[C]//ACM Symposium on Access Control MODELS and Technologies(SACMAT’11). 2011: 51-60.

[11] BRUNS G, FONG P W L, SIAHAAN I, et al. Relationship-based access control: its expression and enforcement through hybrid logic[C]//ACM Conference on Data and Application Security and Privacy(CODASPY’12). 2012: 117-124.

[12] PARK J, SANDHU R, CHENG Y. A user-activity-centric framework for access control in online social networks[J]. IEEE Internet Computing, 2011, 15(5): 62-65.

[13] CHENG Y, PARK J, SANDHU R. A user-to-user relationship-based access control model for online social networks[C]//ACM Conference on Data and Applications Security and Privacy(CODASPY’12). 2012: 8-24.

[14] YUAN C, PARK J, SANDHU R. Relationship-based access control for online social networks: beyond user-to-user relationships[C]//International Conference on Privacy, Security, Risk and Trust (PASSAT’12).2012: 646-655.

[15] PANG J, ZHANG Y. Cryptographic protocols for enforcing relationship-based access control policies[C]//IEEE Computer Software and Applications Conference(COMPSAC’15). 2015: 484-493.

[16] SHUAI H, ZHU W T. Masque: access control for interactive sharing of encrypted data in social networks[C]//International Conference on Network and System Security(NSS’12). 2012: 503-515.

[17] WELLMAN B, BERKOWITZ S D. Social structures: a network approach[J]. American Political Science Association, 1988, 83(4).

[18] 田立勤, 林闯. 可信网络中一种基于行为信任预测的博弈控制机制[J]. 计算机学报, 2007, 30(11): 1930-1938. TIAN L Q, LIN C. A kind of game-theoretic control mechanism of user behavior trust based on prediction in trustworthy network[J]. Chinese Journal of Computers, 2007, 30(11): 1930-1938.

[19] YU J, WANG Y, LI J, et al. Analysis of competitive information dissemination in social network based on evolutionary game model[C]//Cloud and Green Computing(CGC’12). 2012: 748-753.

[20] 张胜兵, 蔡皖东, 李勇军. 一种基于博弈论的社交网络访问控制方法[J]. 西北工业大学学报, 2011, 29(4):652-657. ZHANG S B, CAI W D, LI Y J. A game-theory based access control method suitable for social network[J]. Journal of Northwestern Polytechnical University, 2011, 29(4): 652-657.p

[21] ZHU P, WEI G, VASILAKOS A V, et al. Knowledge sharing in social network using game theory[M]. Springer Berlin Heidelberg, 2012.

[22] 张伊璇, 何泾沙, 赵斌, 等. 一个基于博弈理论的隐私保护模型[J]. 计算机学报, 2016, 39(3):615-627. ZHANG Y X, HE J S, ZHAO B, et al. A privacy protection model base on game theory[J]. Chinese Journal of Computers, 2016, 39(3): 615-627.

Game theory based forwarding control method for social network

SHAN Fangfang1,2, LI Hui1,3, ZHU Hui1,3

1. School of Cyber Engineering, Xidian University, Xi’an 710071, China 2. School of Computer Science, Zhongyuan University of Technology, Zhengzhou 450007, China 3. State Key Laboratory of Integrated Service Network, Xi’an 710071, China

With the rapid development of mobile communication and internet technology, the social network has become one of the mainstream social means used in people’s daily social life. To maintain and strengthen relationships with friends, users may share personal behavior and feelings through social networks. Forwarding these contents may result in privacy leakage. To help publishers make proper data forwarding decision, the benefits of both sides of the forwarding operation were analyzed, and a game theory based forwarding control method for social network was proposed which could effectively prevent dishonest data forwarding operation. By analyzing the benefits of both sides of forwarding operation and considering historical information, the probability of dishonest data forwarding operation was calculated and it was compared with the threshold set by publisher to make the forwarding decision. The procedure and framework of the game theory based forwarding control method was introduced. The benefits of both sides were defined and analyzed. The game play scenario was presented. Some results of experiments are shown to support that the method is effective and it can protect the security of content in social network.

social network, data forwarding control, game theory, Nash equilibrium

TP309

10.11959/j.issn.1000-436x.2018051

2017-11-08；

2018-02-27

李晖，lihui@mail.xidian.edu.cn

国家自然科学基金资助项目（No.61672411, No.U1401251, No.U1504614）；国家重点研发计划基金资助项目（No.2017YFB0802201, No.2017YFB0802203）；陕西省自然科学基金资助项目（No.2016JM6007）

The National Natural Science Foundation of China (No.61672411, No.U1401251, No.U1504614), The National Key Research and Development Program of China (No.2017YFB0802201, No.2017YFB0802203), The Natural Science Foundation of Shaanxi Province (No.2016JM6007)

单芳芳（1984-），女，河南郑州人，西安电子科技大学博士生，主要研究方向为网络安全、云计算安全、信息保护。