MAXGDDP：基于差分隐私的决策数据发布算法

2018-04-19傅继彬张啸剑丁丽萍

通信学报 2018年3期

傅继彬，张啸剑，丁丽萍

傅继彬1，张啸剑1，丁丽萍2

（1. 河南财经政法大学计算机与信息工程学院，河南郑州 450046；2. 中国科学院软件研究所，北京 100190）

基于层次细化的差分隐私决策数据发布得到了研究者的广泛关注，层次节点的选择、分类树的构建以及每层隐私代价的分配直接制约着决策数据发布结果的好坏，也影响最终的数据分析结果。针对现有基于层次细化的决策数据发布方法难以兼顾上述问题的不足，提出一种高效的分层细化方法MAXGDDP，该方法对原始分类数据进行分层细化，在同一层次的概念细化中提出了最大值属性索引算法，在不同层次之间利用类几何分配机制来更加合理地分配隐私预算。基于真实数据集对比了MAXGDDP与DiffGen算法，实验结果表明该方法在保护数据隐私的同时，提高了发布数据的分类准确率。

决策数据；数据发布；差分隐私；层次细化

1 引言

随着信息技术的飞速发展，个人数字信息也在快速增长。对收集到的个人数据进行分析和挖掘能够发现大量有价值的信息，与此同时，数据中所蕴含的敏感信息也有可能被泄露。例如，医院把病人的电子病历数据发布出来，通过对这些数据的分析和挖掘，可以发现各种疾病之间的关系或其他有利于医学进步的信息，但是在该过程中也可能会造成病人隐私的泄露。因此，如何解决数据发布过程中可能存在的隐私泄露问题已经成为一个非常重要的研究课题。

基于-匿名的方法[1]及其变种方法[2~4]是解决数据发布常用的隐私保护技术，然而这类方法通常在特殊的攻击背景知识假设下才能成立。差分隐私保护模型[5,6]的出现为隐私保护数据发布提供了新的方向，它不需要对攻击者的背景知识做任何假设。因此，本文聚焦于满足差分隐私的决策数据发布问题。目前，已有多种基于差分隐私的决策树数据发布方法[7~9]。文献[7]利用指数机制来挑选决策树中的分割属性，尽管该方法利用全部的隐私预算选择最好的分割属性，然而它是基于交互式查询接口构建的决策树，一旦大量的分析者提交查询时，该方法的分类精度就会降低。文献[8,9]结合指数机制确定分割属性，借助于决策树自顶向下地把数据集中所有记录划分到叶子节点中去，然后对叶子节点中的计数值添加拉普拉斯噪声。尽管该类法采用非交互式发布决策数据，然而却存在2个问题：1) 数值属性与非数值属性分开处理，这样需要更多的隐私噪声；2) 自顶向下分割属性时，采用均分的方式处理隐私预算，而均分的方式直接受到树高度的制约。总之，目前还没有一个行之有效的基于差分隐私的方法来统一处理数值属性与非数值属性，并且给出合理的隐私预算分配策略。因此，结合上述分析，本文提出了一种名为MAXGDDP的差分隐私保护算法，其中，MAX表示在属性选择时使用的最大值索引属性选择隐私保护算法，GD表示在不同层次隐私预算分配时采用几何分布机制。该算法的具体创新点如下。

1) 为了能够同时处理数值属性与非数值属性，提出了最大值索引属性选择算法。该方法对数值与非数值属性进行统一处理，并且极大地降低了噪声的规模。

2) 为了合理地分配隐私预算，提出了类似几何策略的预算分配策略。该方法能够把预算尽量预留给决策树的叶子节点。

3) 理论证明所提出的决策树数据发布方法满足-差分隐私。在真实数据上进行了可用性分析，实验结果表明，MAXGDDP优于同类方法。

2 相关工作

决策树（decision tree）是常用的数据分类模型，ID3是经典的决策树学习算法，C4.5是ID3算法的改进。针对决策树数据发布时的隐私问题，主要存在2种隐私保护模型：匿名化模型与差分隐私保护模型。

匿名化模型通常使用数据的泛化操作来起到隐私保护效果，其代表方法包括-匿名[1]、-diversity[2]、-closeness[3]、k-匿名[4]等。-匿名及其变种模型的基本思想是在数据泛化处理后，对于某条记录在数据集中至少有−1个记录具有和它相同的值，这些相同记录被定义为等价组。在等价组中的记录是不可区分的，通过这种方式来保护个人数据的隐私。这类方法的困难在于对攻击者的背景知识建模，Ganta等[10]指出通过不可控的背景知识，个人的隐私可能受到攻击。

差分隐私提供一种严谨并且可操作的隐私定义，基于差分隐私的数据发布和数据分析问题日益受到重视[11~14]。基于差分隐私的数据保护分为交互模式和非交互模式。

在交互模式下，用户不能直接处理数据，只能通过隐私保护的接口进行有次数限制的数据查询，每次查询都要消耗隐私预算。SuLQ-based ID3[15]实现了基于差分隐私保护的ID3算法，在每次计算属性的信息增益时加入Laplace机制的噪声计数值，但加入噪声后导致预测结果准确率下降。PINQ数据分析平台[16]使用Partition算子将查询数据集分割成不相交的子集，利用其计算时并行组合的特点，提高隐私保护预算的利用率，该算法直接利用噪声计数值评估信息增益标准，再使用ID3算法生成决策树。由于信息增益的计数值需要对每个属性进行计算，所以需要将整个隐私预算分配到每次查询中，导致每次查询的隐私预算较小，当数据集较大时将引入大量噪声。文献[7]提出了基于指数机制的Differential Private ID3和C4.5算法，指数机制在一次查询中同时评估所有属性，减少了噪声和隐私预算的浪费，指数机制可以挑选属性分割点。该算法在处理大量查询时分类精度有所降低。

而非交互模式的隐私保护算法是对数据进行处理并且发布处理后的合成数据库，用户能对发布的合成数据库进行任意处理[17]。如何合理分配隐私预算，并尽可能提高发布数据的可用性，是非交互式发布主要面临的问题。

文献[8,9]分别提出了针对决策树分析的差分隐私数据发布算法DiffGen[8]与DT-Diff[9]。这2种算法采用“自顶向下、逐步细分”的策略，首先将数据集完全泛化，然后进入细分迭代循环。该算法利用指数机制进行属性选择，利用拉普拉斯机制进行记录计数的随机化。虽然这2种算法满足-差分隐私保护要求，但其缺点在于没有充分利用给定的隐私预算，导致加入不必要的冗余噪声。

Fletcher等[18]利用信噪比技术构建随机决策树来发布决策数据，然而该方法利用均分的方式来处理隐私预算。Cormode等[19]在空间数据分割的隐私保护研究中提出了四分树、kd树层级之间的隐私代价几何分配策略。但是决策树和四分树、kd树的结构是不同的，它在层次之间没有固定的扇出数。

基于对以上相关工作的分析，本文提出了MAXGDDP方法来发布决策树数据，它利用最大值索引属性选择算法挑选分割属性进行层次细化，在不同层次推导出基于决策树的类几何分布隐私预算分配策略。该方法不但满足差分隐私，同时还能够发布比较精确的结果。

3 定义与理论基础

3.1 差分隐私相关定义

差分隐私保护方法可以确保在某一数据集中插入或删除一条记录的操作不会影响计算的输出结果。另外，该保护模型不关心攻击者所具有的背景知识，即使攻击者已经掌握除某一条记录之外的所有记录的信息，该记录的隐私也无法被披露。差分隐私的形式化定义如下。

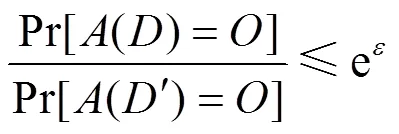
其中，概率Pr[·]是由算法的随机性控制，也表示隐私被披露的风险；隐私预算参数表示隐私保护程度，越小，隐私保护程度越高。

从定义1可以看出，差分隐私技术限制了任意一条记录对算法输出结果的影响。该定义是从理论角度确保算法满足-差分隐私，而要实现差分隐私保护需要噪声机制的介入。

常用的差分隐私机制分别为拉普拉斯机制与指数机制。而基于不同噪声机制且满足差分隐私的算法所需噪声大小与全局敏感性密切相关，全局敏感度的定义如下。

定义2 对于任意一个函数:R，函数的全局敏感度为

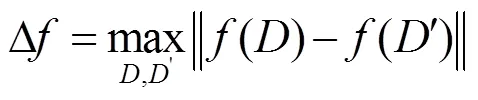
其中，和至多相差一条记录，表示所映射实数空间，表示函数的查询维度，通常使用1度量距离。

拉普拉斯机制[20]通过对真实输出值加入拉普拉斯分布的噪声进行扰动来实现差分隐私保护。

而指数机制[21]主要处理一些输出结果为非数值型的算法，例如，决策树分类算法中属性分裂选择问题。该机制的关键是设计一个效用函数，指数机制的定义如下。

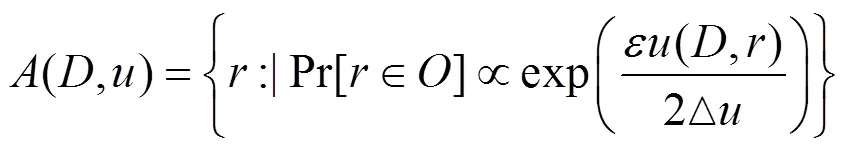
3.2 决策树

决策树是一种简单但是广泛使用的分类预测模型，树中每个节点表示某个概念属性，而每个分叉则代表该属性不同的取值，每个叶节点则对应从根节点到该叶节点路径所表示的分类过程。

决策树算法根据训练集构建一个决策树，利用这个决策树可以对测试数据进行分类处理。决策数有2个优点：1) 决策树模型可读性好，具有描述性，有助于人工分析；2) 效率高，决策树只需要一次构建，反复使用，每一次预测的最大计算次数不超过决策树的深度。

决策树构建的基本步骤如下：1) 将所有记录看作一个节点；2) 遍历每个属性的每一种分割方式，找到最好的分割属性；3) 根据最佳分割属性的取值分割成个节点1,…,N；4) 对1,…,N分别继续执行步骤2)~步骤3)，直到满足某种分类条件为止。

决策树的属性根据处理方式的不同可以分为2种：数值型和非数值型。其中，数值型属性可以用整数或浮点数表示，如“年收入”“年龄”等属性。选定一个数值作为分割点后，每个记录根据自己该属性值大于或小于该分割点分为2个集合。非数值属性类似编程语言中的枚举类型，变量只能从有限的选项中选取，例如，“婚姻情况”只能在“单身”“已婚”或“离婚”中选择。如果非数值属性被选择为分割属性，每个记录根据自己该属性值，分为若干个集合。

在决策树算法中决定使用哪个属性进行分割是一个核心的问题。有很多度量方法来评估分割属性的好坏，例如，信息增益、信息增益率、最大记录等。本文主要使用最大记录数度量，定义如下

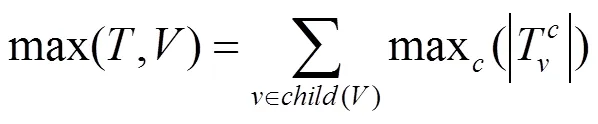
最大记录是对各个分支中分类结果最大的数据记录总和，该函数的敏感度为1。

3.3 基于泛化的非交互数据发布

在数据发布的隐私保护中，本文采用了泛化的方法。它的思想是用泛化值去替换原有的细化值以保护原有信息的隐私。例如，数据中的年龄信息，它是一个数值属性，假设某个人年龄为25，经过泛化处理会变为一个范围，如18~65。在每个属性进行泛化的过程需要一个表示概念泛化关系的分类树。树的根节点是一个最泛化的概念Any，每个子节点是父节点的具体化的分类，图1为国籍属性的分类树。

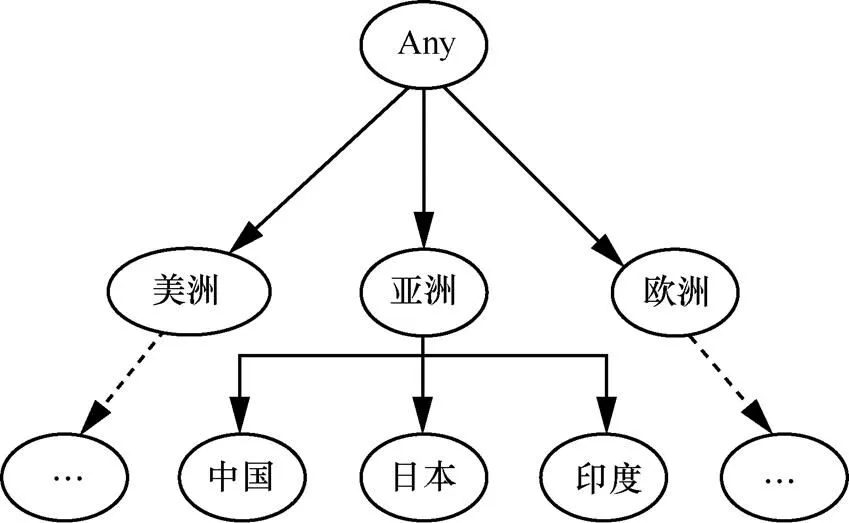
图1 国籍属性的分类树

4 MAXGDDP数据发布算法

针对上述问题，本文提出了MAXGDDP算法。在分类数据的处理过程中采用逐层分割的思想，首先把所有的记录压缩到一个根节点，然后结合分割标准自顶向下分割，最后叶子节点存放分类的记录分区。然而在分割过程中，如何选择一个属性进行分割是分类数据发布的关键。针对分割属性的选择，提出了最大值索引属性选择算法（MAXDP），该算法对数值属性和非数值属性进行统一处理。同时，在树结构的不同层次之间利用类几何分布策略进行隐私预算分配。

4.1 最大值索引属性选择（MAXDP）算法

分类数据的发布过程中，如何选择一个好的分割节点，同时保护每个分割节点中真值计数不被泄露，是一个关键的问题。针对这个问题，本文提出一个满足差分隐私的分割点选择（MAXDP）算法。

该方法把决策树同一层的数值属性和非数值属性统一处理，而且极大地降低了隐私保护噪声的规模。该方法使用最大记录数作为选择分割属性的度量方法。在传统的决策树算法中，非数值属性如在某个数据集中的属性“天气”，它的值有3种可能，分别是“晴朗”“多云”“下雨”。根据这个属性的值可以把数据记录分为3类，根据记录的分类可以计算出该属性的最大记录数值。而对于数值属性首先要确定其分割点，例如，在某个数据集中的属性“年龄”，其取值范围是整数[18,65]，需要确定某个分割点把数据分为2类，所以首先要算出最优分割点，然后把记录分类，并计算该属性的最大记录数值，最后才可以把数值属性和非数值属性放在一起比较，选择出最优分割属性。所以数值属性的处理和非数值属性的处理流程不同，数值属性分为2步，需要更多的隐私预算。

MAXDP算法对于每个非数值属性（如国籍属性），只需要计算出一个最大记录数度量值；而数值属性（如年龄为[18,65]，在18~65之间有多种分割方式），需要对所有可能的分割点进行最大记录数度量值的计算，即一个属性对应多个最大记录数值。本文把所有的计算结果放在一个统一的向量中，如图2所示。每个非数值属性对应向量中一个空间，每个数值属性对应向量中一组连续的空间，每个空间点对应数值属性可能分割点的最大记录数值。

图2 MAXDP中的属性选择向量结构

为了计算方便，把所有的计算结果放在一个向量0中，0=<1,2,…,c>，其中，c表示从该属性进行分割的最大记录数。为了寻找分割节点，需要搜索簇0中的最大值。而在寻找0中的最大值时，如果不采用噪声机制进行扰动，则会泄露该分割节点所包含的具体计数值。获得具体计数后，攻击者即可推测出某些记录属于哪些具体的类别，进而导致个人的隐私信息泄露。

一种最直接的方法是对0中每个计数添加ε拉普拉斯噪声，其中，ε表示分割树的第层所分得的隐私预算。输出后比较大小，进而获得最大值。然而该方法所挑选出的最大值非常不准确，其原因是∆=。例如，c=12、∆=100、ε=0.1，则相当于以1 000倍的噪声对c进行扰动，进而c的真实值发生很大的扭曲。

通过分析决策树的工作原理发现，没有必要输出0中所有的噪声值进行比较来获得最大值。只要获得0中最大值所处的位置即可，即最大值的索引位置。如果返回的索引指向一个非数值属性，对这个非数值属性进行树的扩展，如果返回的索引落在某个数值属性的可能分割点的区间内，利用该索引指向的数值进行分割点的确定，并且进一步进行树的扩展。

MAXDP算法使∆1，进而极大降低了隐私保护噪声的规模。接下来，需要证明输出最大值索引位置的过程满足ε-差分隐私。

定理1 MAXDP满足ε-差分隐私。

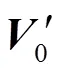
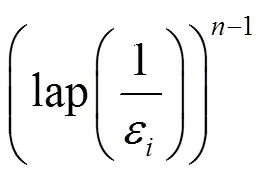
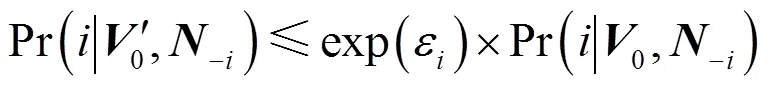
首先证明式(6)成立。

因此，式(6)成立。

同理，可以推理出式(7)也成立。

进而，可证明MAXDP满足ε-差分隐私。

4.2 基于类几何策略的隐私预算分配方法

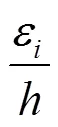
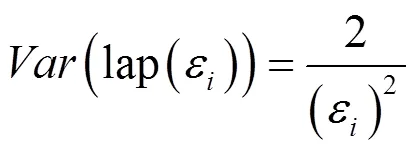
则决策树所携带的总体误差可以表示为

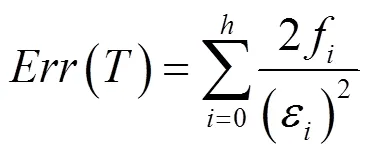
其中，f表示第层的总扇出数。

因此，将为决策树每层分配合理预算转化为使目标函数()最小的优化问题，即

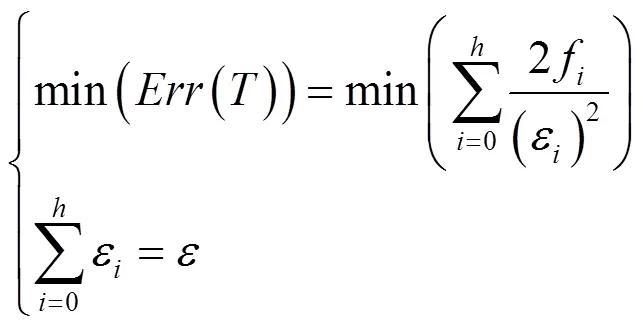
证明通过Cauchy-Schwarz不等式可知

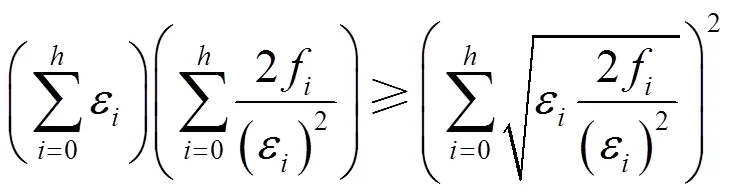
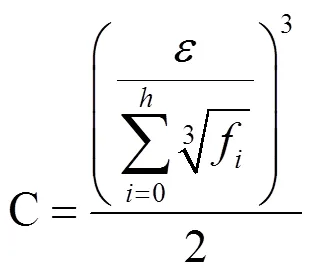
因此，有

由此可知，每层的隐私预算是与分类树的各层扇出有关的，并且在各个层次之间，隐私预算与扇出的关系为

因为决策树中第层扇出f，总是大于第−1层总扇出f1，所以ε是递增的，在更深的层次应该分配更多的隐私预算，这有利于数据更为准确的发布。

在决策树的构建过程中，各个层次总扇出和决策树的总扇出是在选择隐私预算之后计算最佳属性之后才能得到，所以在计算每个层次的隐私预算时，假设=3，即可获得=。

由等比数列公式可得ε，即

4.3 MAXGDDP算法描述

MAXGDDP算法从最泛化概念开始，通过一系列符合隐私保护的操作对数据进行细分处理。在进行决策树构建的过程中，选择最佳分割属性时采用MAXDP算法。各层次之间采用类几何分布策略分配隐私预算，整个算法的过程如算法1所示。

算法1 MAXGDDP

输入初始数据集，隐私预算，细化层次

1) 对数据集中每个属性进行初始化A=Any，其中，Any为最泛化的概念，所有的记录放在一个初始化分区中。

2) 把整个隐私预算分为2个部分，1+2=。

3)for=1 to

4) 计算该层的隐私保护预算

5) 计算分区中所有属性的最大记录数度量值。非数值属性计算出一个值，数值属性对每个可能的分割点计算，得出一组值，把这些数组放在一个向量中，利用MAXDP算法选择某个属性A

6) 利用属性A的细化概念层次对数据集进行细化，并且数据集合根据细化概念进行分区

7) 更新所有分区中记录的统计计数值，并在新分区重新进行以上计算

8) end for

对于整个算法，隐私预算分为2个部分，在决策树的建立过程中使用1，在对叶子节点分区记录计数进行随机化时使用2，对每个分区的记录数利用拉普拉斯机制添加lap噪声。根据定理3可知，MAXGDDP算法满足-差分隐私。

5 实验结果与分析

实验中用C++实现了MAXGDDP隐私保护数据发布算法。实验机器配置为2.10 GHz 6核Xeon CPU，32 GB内存。在实验数据方面，采用了3个UCI数据集Iris、Adult和Census Income。Iris数据集如表1所示，共有4个数值型的预测属性，分类结果为3类，数据共有150条记录。

表1 Iris数据集

Adult数据集如表2所示，共有14个预测属性，其中，数值型有6个，非数值型有8个，分类结果有2类，数据集中去掉了属性值未知的记录，共有45 222条记录。

表2 Adult数据集

在3个数据集中，Census Income数据集的属性和记录数都较多，共有40个属性，其中，7个数值属性，33个非数值属性，数据集中去掉了属性值未知的记录，共有14 2521个记录。

在MAXGDDP算法进行概念细化的过程中，每个数据集的每个属性都需要一个分类树集合来配合算法的逐层细化计算。分类树中记录了每一个属性的细化过程。例如，在Adult数据集中的education-num（教育年限/数值属性）的分类树结构如下

{1-20 {1-12 {1-5} {5-12}} {12-20 {12-16} {16-20}}}。

workclasst（工作类别/非数值型属性）的分类树结构如下

{Any {Worked {With-Pay {Private} {Self-emp {Self-emp-not-inc }{Self-emp-inc }} {Gov {Federal-gov}{Local-gov}{State-gov}}} {Without-pay}} {Never-worked}}。

对每一个数据集进行处理的过程中，首先确定该层次的隐私预算，然后在同一层次中对数据集中的每个属性计算最大记录值，对于非数值属性得到一个值，对于数值属性得到多个值（每个值对应于每个可能的分割点），把这些数值放在一个向量中，利用最大值索引属性选择算法返回最大值的索引位置，通过该位置确定要进行分割的属性，根据分类树的结构确定要细化的概念，并且通过属性值的不同把数据集分到不同的数据分区中。重复该过程直到细化层次满足要求。

在实验数据细化的过程中，需要加入随机性以保证差分隐私，在每次实验中选择属性具有随机性，所以本文对每个实验都执行10次，然后计算平均的分类准确率。

为了评估MAXGDDP算法中隐私保护措施对数据分类性能的影响，首先，采用经典决策树算法C4.5对原始数据集合进行训练和分类，把这个原始数据中的准确率作为基线（baseline）；然后，利用MAXGDDP算法对各个原始数据集进行隐私保护的处理，生成泛化处理后的合成训练集和测试集；最后，仍然采用C4.5算法，对合成训练集进行决策树的训练，利用得到的决策树对合成测试集进行分类，评估其准确率，结果如图3所示。

图3(a)为MAXGDDP算法在Iris数据集中的评估结果。该数据集包含3个类别，共150条记录。从3个类别中平衡选择100条记录作为训练集，50条记录作为测试集。图3(a)横坐标为细分层数，纵坐标为合成数据集最终的分类准确率，最上面的线是原始数据集的基线分类准确率（94%），4条曲线为隐私保护预算分别在=0.10, 0.25, 0.50, 1.00条件下各个细化层次的准确率情况。在隐私保护预算为1.00，细分层数为5时，获得最好的分类准确率（92.98%）。

图3(b)为MAXGDDP算法在Adult数据集中的评估结果。Adult数据集是很多隐私数据发布算法都采用的数据集。该数据集共有14个预测属性，其中，有6个数值属性和8个非数值属性。该数据集共有45 222条记录，把其中30 148条记录作为训练集，剩余的15 074条记录作为测试集。本文评估了MAXGDDP算法在不同细化参数（=4,7,10,13,16）、不同隐私保护预算（=0.10, 0.25, 0.50, 1.00）的情况。图3(b)最上面的线是原始数据集的基线分类准确率（85.3%），MAXGDDP算法在细化参数为13，隐私保护预算为1.00时，获得最好的分类准确率（83.72%）。

图3(c)为MAXGDDP算法在Census Income数据集中的评估结果，该数据集有142 521条记录，40个属性，其中，数值属性7个，非数值属性为33个。该数据集的数据量比前2个数据集更大，所以分配了更多的隐私预算。图3(c)最上面的线是原始数据集的基线分类准确率（95.6%，），MAXGDDP在细化参数为10，隐私保护预算为2.00时，获得最好的分类准确率（94.7%）。MAXGDDP在该数据集上取得了更好的性能，说明该算法具有较好的数据扩展性。

图3 MAXGDDP算法在3个数据集中的结果

Mohammed等[8]提出的DiffGen算法是一个经典的分类数据发布算法，为了评估MAXGDDP算法，在3个数据集对2种算法进行了比较。首先，为了比较不同隐私预算对2种算法的影响，在3个数据集中使用某个固定细分层数，分别使用2种算法对数据进行隐私保护的发布处理，不同隐私预算下的结果如图4所示。

图4 不同隐私预算条件下的比较结果

在图4(a)中，Iris数据集固定细分层数为5，比较不同隐私代价（=0.10, 0.25, 0.50, 1.00）下2种算法的准确率可以看出，在隐私代价较小时MAXGDDP的优势较为明显。

在图4(b)中，Adult数据集固定细分层数为15，比较不同隐私预算（=0.10, 0.25, 0.50, 1.00）下2种算法分类准确率可以发现，MAXGDDP算法在不同的隐私预算条件下，分类准确率都优于DiffGen算法。

在图4(c)中，Income数据集细化参数固定为10，在不同的隐私预算（=0.50, 0.75, 1.00, 2.00）下比较2种算法最终的准确率。Census Income数据集具有更大的数据量，在该数据中的结果可以看作不同算法在数据扩展性方面的性能。可以看出，MAXGDDP算法在数据量较大的情况下取得更好的分类准确率结果。

综合分析3个数据集的结果，MAXGDDP更有效地使用了隐私预算。所以在Iris数据集中，较小隐私预算条件下的MAXGDDP算法取得了较好效果，而且优势比较明显，因为属性较少的情况下，分割属性选择的准确与否对结果影响很大。在规模较大的2个数据中，MAXGDDP在隐私预算较小时也取得了较为明显的优势，在隐私预算较为充足时也优于DiffGen的效果，但是差别不是很大，因为在属性较多的情况，某个属性的选择对结果的影响不像小数据中那么大。

为了评估不同细分层数对2种算法的影响，在固定隐私保护预算的情况，对2种算法在不同数据集进行评估，结果如图5所示。

图5(a)为在Iris数据集固定隐私保护预算为0.50，细分层数（=2,3,4,5,6）下2种算法的分类准确率。从中可以发现，MAXGDDP算法在不同细化层次的条件，其分类准确率都优于DiffGen算法。

图5(b)为在Adult数据集中固定隐私保护预算为0.50，细分层数（=4,7,10,13,16）下2种算法的分类准确率结果。在细分层数为13时，2种算法均得到最高的分类准确率，而且MAXGDDP算法在各个细分层数上均优于DiffGen算法。

图5(c)是2种算法在Income数据集中的结果。在固定隐私保护预算为0.50的条件下，比较不同的细分层数（=4, 7, 10, 13）2种算法的分类准确率。从图5(c)中可以发现，MAXGDDP算法在较少细分层次条件下，优势较为明显，总体而言，在不同细化层次的条件，其分类准确率都优于DiffGen算法。

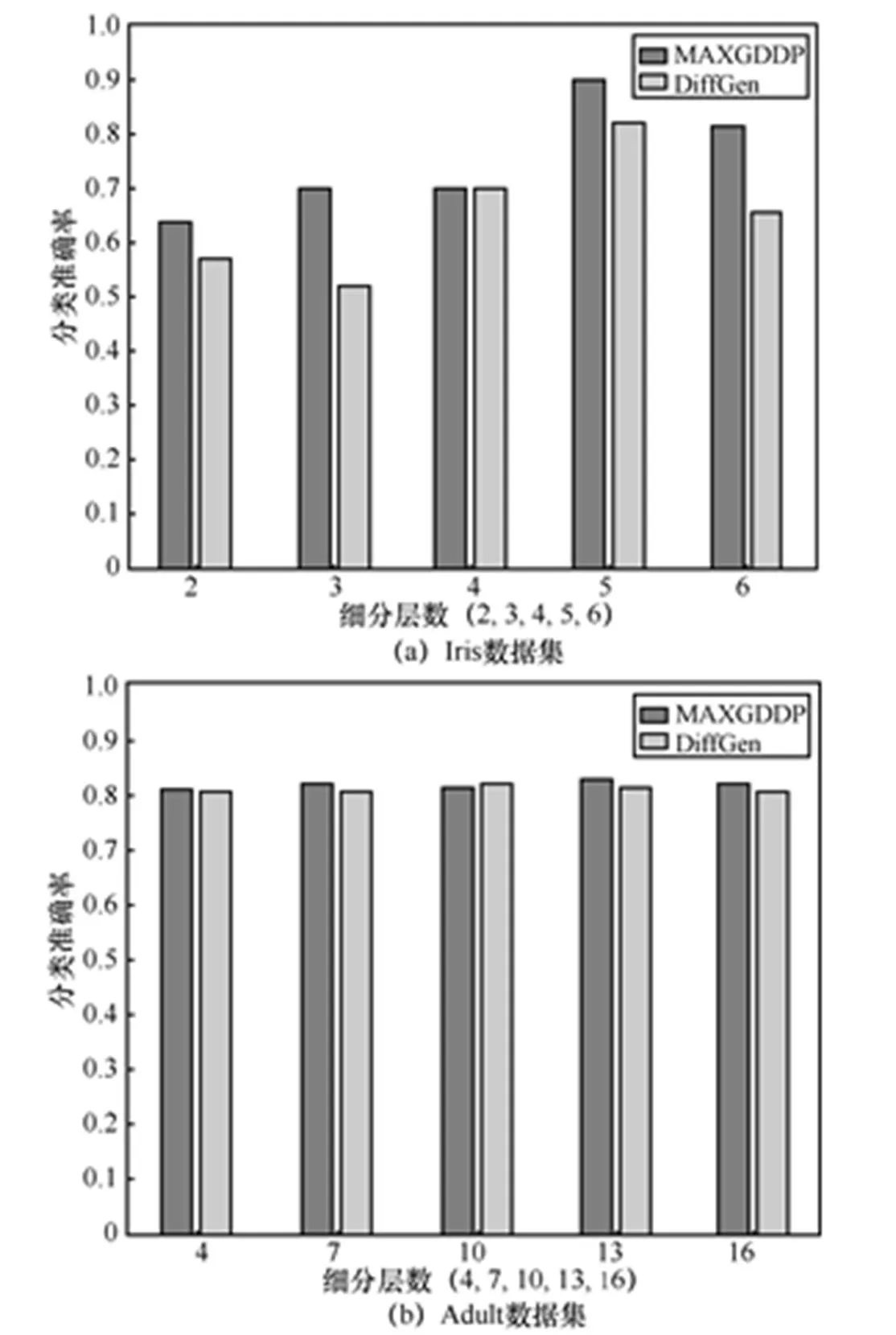
图5 不同细分层数条件下的比较结果

MAXGDDP算法实际上包括计算最佳属性索引位置的MAXDP算法和决策树不同层次之间的几何策略隐私预算分配方法。本文通过实验评估了MAXDP算法和隐私预算分配算法的作用，结果如图6所示。图6中上面曲线是MAXGDDP算法叠加产生的分类准确率，下面曲线是在MAXDP和决策树层次间采用隐私预算平均分配的结果。2条曲线之间差值可以看作几何策略分配算法对分类准确率的作用。从图6可以发现，几何分布算法在不同数据集中对分类准确率的提升都有一定的作用。

图6 隐私预算几何分布的影响

6 结束语

本文提出的MAXGDDP算法用于隐私保护数据发布，在保护数据中敏感信息的同时保持数据的可用性。针对决策树算法的特点，在选择细化属性时，利用MAXDP隐私保护算法计算最佳属性的索引位置。在决策树不同层次之间，利用决策树层次的几何分布更加合理地分配隐私预算。本文通过理论证明了该算法满足差分隐私，并且通过实验也表明该方法的有效性。

目前，MAXGDDP算法是利用静态数据进行隐私保护的数据发布，但是随着互联网信息资源的数量和重要性不断增长，从互联网上获取知识变得越来越重要，互联网环境数据的显著特征是动态更新，这种数据随时更新的数据环境称为动态数据环境。下一步的工作主要研究在动态数据环境下基于差分隐私的数据发布算法。

[1] SWEENEY L.-anonymity: a model for protecting privacy[J]. International Journal of Uncertainty, Fuzziness and Knowledge-Based Systems, 2002, 10(5): 557-570.

[2] MACHANAVAJJHALA A, KIFER D, GEHRKE J, et al.-diversity: privacy beyond-anonymity[J]. ACM Transactions on Knowledge Discovery from Data (TKDD), 2007, 1(1): 3-52.

[3] LI N, LI T, VENKATASUBRAMANIAN S.-closeness: privacy beyond-anonymity and-diversity[C]//2007 IEEE 23rd International Conference on Data Engineering. 2007: 106-115.

[4] TERROVITIS M, MAMOULIS N, KALNIS P. Privacy-preserving anonymization of set-valued data[C]//Very Large Data Base Endowment. 2008: 115-125.

[5] DWORK C. Differential privacy[C]//33rd International Colloquium on Automata, Languages and Programming, part II (ICALP 2006). 2006: 1-12.

[6] DWORK C, LEI J. Differential privacy and robust statistics[C]//The 41th Annual ACM Symposium on Theory of Computing (STOC).2009: 371-380.

[7] FRIEDMAN A, SCHUSTER A. Data mining with differential privacy[C]//The 16th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining.2010: 493-502.

[8] MOHAMMED N, CHEN R, FUNG B, et al. Differentially private data release for data mining[C]//The 17th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining. 2011: 493-501.

[9] ZHU T, XIONG P, XIANG Y, et al. An effective deferentially private data releasing algorithm for decision tree[C]//12th IEEE International Conference on Trust, Security and Privacy in Computing and Communications.2013: 388-395.

[10] GANTA S R, KASIVISWANATHAN S P, SMITH A. Composition attacks and auxiliary information in data privacy[C]//The 14th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining. 2008: 265-273.

[11] ZHU T, LI G, ZHOU W, et al. Differentially private data publishing and analysis: a survey[J]. IEEE Transactions on Knowledge and Data Engineering. 2017, 29(8): 1619-1638.

[12] 熊平, 朱天清, 王晓峰. 差分隐私保护及其应用[J]. 计算机学报, 2014, 37(1): 101-122.

XIONG P, ZHU T Q, WANG X F. A survey on differential privacy and applications[J]. Chinese Journal of Computers, 2014, 37(1): 101-122.

[13] 康海燕, 马跃雷. 差分隐私保护在数据挖掘中应用综述[J]. 山东大学学报: 理学版, 2017(3): 16-23.

KANG H Y, MA Y L. Survey on application of data ming via differential privacy[J]. Journal of Shangdong University(Natural Science), 2017(3): 16-23.

[14] 张啸剑, 孟小峰. 面向数据发布和分析的差分隐私保护[J]. 计算机学报, 2014, 37(4): 927-949.

ZHANG X J, MENG X F. Differential privacy in data publication and analysis[J]. Chinese Journal of Computers, 2014, 37(4): 927-949.

[15] BLUM A, DWORK C, MCSHERRY F, et al. Practical privacy: the SuLQ framework[C]//The Twenty-Fourth ACM SIGMOD-SIGACT- SIGART Symposium on Principles of Database Systems. 2005: 128-138.

[16] MCSHERRY F D. Privacy integrated queries: an extensible platform for privacy-preserving data analysis[C]//The 2009 ACM SIGMOD International Conference on Management of Data.2009: 19-30.

[17] GOSWAMI P, MADAN S. Privacy preserving data publishing and data anonymization approaches: a review[C]//2017 International Conference on Computing, Communication and Automation. 2017: 139-142.

[18] FLETCHER S, ISLAM M Z. A differentially private random decision forest using reliable signal-to-noise ratios[C]//Australasian Joint Conference on Artificial Intelligence. 2015: 192-203.

[19] CORMODE G, PROCOPIUC C, SRIVASTAVA D, et al. Differentially private spatial decompositions[C]//IEEE 28th International Conference on Data Engineering.2012: 20-31.

[20] DWORK C, MCSHERRY F, NISSIM K, et al. Calibrating noise to sensitivity in private data analysis[C]//Theory of Cryptography Conference. 2006: 265-284.

[21] MCSHERRY F, TALWAR K. Mechanism design via differential privacy[C]//48th Annual IEEE Symposium on Foundations of Computer Science. 2007: 94-103.

MAXGDDP: decision data release with differential privacy

FU Jibin1, ZHANG Xiaojian1, DING Liping2

1. College of Computer & Information Engineering, Henan University of Economics and Law, Zhengzhou 450046, China 2. Institute of Software, Chinese Academy of Sciences, Beijing 100190, China

Specialization-based private decision data release has attracted considerable research attention in recent years. The relation among hierarchical node, taxonomy tree, and budget allocation directly constrains the accuracy of data release and classification. Most existing methods based on hierarchical specialization cannot efficiently address the above problems. An effective method was proposed, called MAXGDDP to publish decision data with specialization. MAXGDDP employed MAX index attribute selection algorithm to select the highlight concept for furthering specialization in each hierarchy. Besides, for making more rational use of privacy budget, MAXGDDP relied on geometric strategy to allocate the privacy budget in each hierarchy. Compared with existing methods such as DiffGen on the real datasets, MAXGDDP outperforms its competitors, achieves data privacy and the better result of classification simultaneously.

decision data, data release, differential privacy, hierarchical specialization

TP309

10.11959/j.issn.1000-436x.2018049

2017-07-20；

2018-02-27

国家自然科学基金资助项目（No.61502146, No.91646203, No.91746115）；河南省自然科学基金资助项目（No.162300410006）；河南省科技攻关基金资助项目（No.142102210384, No.172102310713）；河南省教育厅高等学校重点科研基金资助项目（No.16A520002）；河南省青年骨干教师基金资助项目；河南财经政法大学青年拔尖人才资助计划基金资助项目

The National Natural Science Foundation of China (No.61502146, No.91646203, No.91746115), The Natural Science Foundation of Henan Province (No.162300410006), The Key Technologies R&D Program of Henan Province (No.142102210384, No.172102310713), The Research Program of The Higher Education of Henan Educational Committee (No.16A520002), Foundation for The Excellent Youth Teacher of Henan Province, The Young Talents Fund of Henan University of Economics and Law

傅继彬（1975-），男，河南许昌人，博士，河南财经政法大学副教授，主要研究方向为知识工程、机器学习、隐私保护等。