基于贝叶斯模型的驾驶行为识别与预测

2018-04-19王新胜卞震

通信学报 2018年3期

王新胜，卞震

基于贝叶斯模型的驾驶行为识别与预测

王新胜，卞震

（江苏大学计算机科学与通信工程学院，江苏镇江 212013）

针对智能驾驶系统处理大量驾驶数据时出现的效率和精度不足的问题，提出一种基于贝叶斯模型来处理驾驶数据，识别和预测人类驾驶行为的方法。该方法可以无监管地通过驾驶数据对应地推断出具体驾驶行为，共分为2步：第一步，通过贝叶斯模型分割算法将惯性传感器收集到驾驶数据分割为近线性分段；第二步，通过LDA拓展模型将线性分段聚集为具体的驾驶行为（如制动、转弯、加速和惯性滑行）。离线实验和在线实验结果表明，在处理大量驾驶数据的情况下，该方法效率和识别精度更高。

驾驶数据；贝叶斯模型；惯性传感器；线性分段

1 引言

随着科技的快速发展，车载传感器的数量与日俱增，带来了汽车驾驶数据量的快速增长[1]。从低层次的机械诊断信息如发动机的状态到更加高层次的防抱死制动系统和电子稳压数据，基于不同传感器技术的驾驶员辅助系统（ADAS）在不断快速发展[2]。先进的ADAS可以提供车道偏离警告、交通信号识别、自适应巡航控制、自动停车和碰撞规避等功能[3]。虽然这些数据是分析驾驶员行为、交通状况和开发未来安全系统的重要来源，但其生成速度快且数据量过大，专家们无法在有效时间或成本效益内对这些数据进行分析[4,5]。在大规模的车辆驾驶行为研究的情况下，这种问题更加突出[6,7]。

同样，智能车辆面临的问题是必须能够及时地将大量驾驶数据处理成简明而有意义的结果。而目前的ADAS无法形成对环境的高度了解。相反，它们仅限于车辆及其周围环境数据的处理和反馈。单靠这种做法，对于长期、预期的驾驶来说是不够的。为了使车辆对潜在风险做出全面的反馈，并避免与驾驶员的直觉相冲突，ADAS未来的发展必须全面考虑驾驶员的行为、意图以及道路交通环境信息[8]。本文的目的就是通过分析低层次的自然数据形成对世界的高层次了解。因此，无论是处理大量历史数据还是分析实时数据，都需要一个无需人为监管就能够处理大量复杂数据的方法。目前，该方法面临着许多需要解决的问题，主要包括处理数据所需的准确性、车辆速度带来的时间限制和数据处理过程带来的时延以及道路环境等问题。其中，道路环境是必须要重点解决的问题，因为当环境与获取的实验数据的测试环境不相同时，往往容易得出错误的结果。此外，该方法必须能够适应各种少见的道路状况，满足长期使用的需求[9]。

通过研究发现，使用贝叶斯模型[10]来进行驾驶行为的识别和预测可以很好地解决上述问题。贝叶斯模型具有以下优点：1) 使用贝叶斯模型能对信息的价值或是否需要采集新的信息做出科学的判断，能对实验结果的可能性加以数量化的评价，而不是像一般的决策方法那样，对结果完全肯定或完全否定，提高了结果的准确性[11]；2) 贝叶斯模型将先验概率或主观概率这2种信息巧妙地结合起来；3) 便于对3层贝叶斯概率模型（也称为LDA, latent Dirichlet allocation）进行拓展[12]；4) 贝叶斯模型可以在处理数据的过程中根据具体情况做出相应的变化，逐步完善数据模型，使得出的结果更加科学，能够满足长期使用的需求[13]；5) 使用贝叶斯模型无需人为监管且只需要少量的数据预处理，计算效率高，能满足驾驶信息处理问题中实时性的需要。

为此，本文提出一个基于贝叶斯模型的方法来解决智能驾驶系统处理大量驾驶数据时出现的效率和精度不足的问题。

表1 驾驶行为识别与预测方法比较

2 相关工作

研究表明，人类在驾驶时，倾向于使用多个简单的操作而不是执行单一复杂的操作[14]。基于这一原则发现，当驾驶员在驾驶车辆的过程中，对应车辆在短时间内是线性或近线性状态运动的。根据这一发现，大量研究工作得以展开并且构建了相应的数学模型，已达到将自然驾驶数据序列同时划分为多个非重叠的线性分段，并将这些分段聚集成对应的高级驾驶行为的目的。

文献[15,16]中都提出了基于分段自回归模型分析驾驶数据以推断驾驶行为的方法。但是这2个文献都只是使用模拟数据对它们的模型进行相应的测试，无法保证在线实验环境中对应算法的实时性。文献[17]使用贝叶斯非参数模型来分析驾驶数据。在文献[18]中，也使用了文献[17]中提出的模型，并且将该模型与LDA模型相结合，以此来将抽象的线性分段与具体的驾驶行为相联系。尽管得出的结果比较理想，但是该模型在计算上有着相当大的固有复杂性。此外，测试的结果还受到测试环境的影响，不同的测试环境导致其测试的结果也不相同。

文献[19]提出了使用惯性测量单元（IMU）来收集数据，结合照相机的图像来推断驾驶行为的方法。该方法由2个部分组成：首先，使用了文献[20]中提出的变点检测方法，将IMU收集的数据分割成不重叠的线性分段；然后，将线性分段和相机图像片段相关联，以此得出具体的驾驶行为。而文献[21]提出了一种通过区分不同的驾驶风格，以识别对应驾驶人员信息的方法。同样，该方法还是需要分割惯性数据。但与文献[19]中提出的方法不同的是，分割过程是通过使用阈值和车辆信号，如刹车灯来完成的。类似地，文献[22]中也是使用阈值和移动的平均值来分割车载传感器收集的惯性数据。表1给出了上述方法的比较结果。

针对上述方法中存在的问题，本文在文献[17]和文献[18]的基础上，提出一种不需要监管的、高效的方法来识别与预测驾驶行为，即基于贝叶斯模型的方法。与文献[21,22]提出的方法不同的是，本文所提方法不依赖于阈值或外部信号；与文献[19]中提出方法相比较，本文所提方法有着完全贝叶斯、不需要监管的优点；与文献[15,16]中提出的方法不同的是，本文所提方法不受测试数据的影响，并且可以推广到新的环境中。此外，本文方法考虑了坡度对驾驶数据的影响，对驾驶员行为的识别更加准确。

3 驾驶数据分析

在统计学领域，有许多关于变点检测与序列分割模型的研究[23]。本文所提基于贝叶斯模型的驾驶行为识别与预测方法，其基本思想是引入统计学中的变点检测方法并结合贝叶斯多元线性回归模型来实现车辆运动数据序列的分割，进而使用LDA拓展模型，对分割序列与具体的驾驶行为之间进行映射。

3.1 贝叶斯多元线性回归模型构建

首先，通过样本数据得到似然函数，给出先验分布；然后，结合先验分布得到数据模型的后验分布并且计算出数据的边缘似然估计；最后，对于给定的新测试数据，利用之前得到的后验分布作为权重，在整个参数空间里计算加权积分，得到预测分布，实现贝叶斯多元线性回归模型的构建。

3.1.1 似然函数

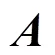
3.1.2 参数的共轭先验分布

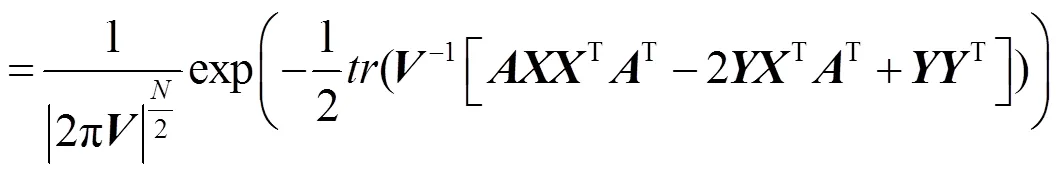
在给定条件下，关于和的共轭先验分布服从矩阵正态—逆分布，其密度函数描述如式(3)所示。

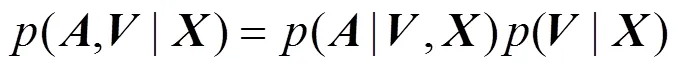
3.1.3 参数的后验分布

根据贝叶斯定理，共轭先验分布密度正比于似然函数，即

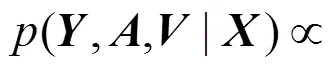
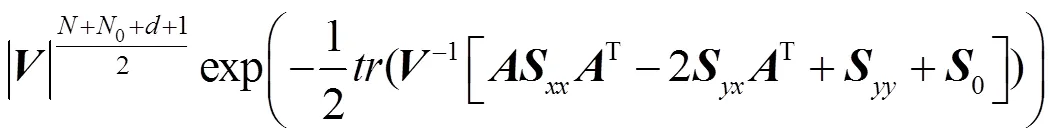
由于共轭，所以参数和的后验分布具有对应的先验分布(3)相同的数学形式。所以后验分布为

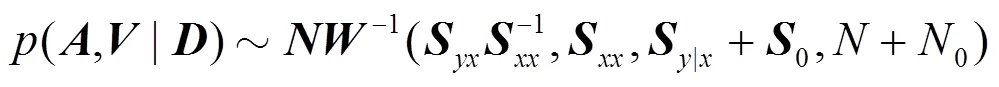
3.1.4 数据的边缘似然估计

通过对似然函数中模型参数边缘化，得出数据的边缘似然估计，其密度函数为

上述的积分可以计算求值，其结果可以用2个常数的比值来表示，其中，分子和分母分别与超参数先验和后验分布相关联，数学计算式为

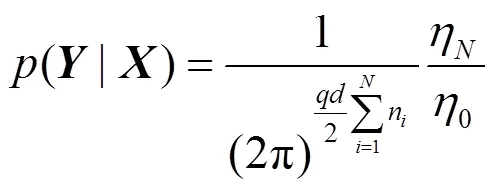
3.1.5 预测分布

3.2 序列分割方法

本节将应用多元线性模型的理论来解决数据序列分割的问题。

为此进行以下假设：1) 在每个分段内，模型系数和噪声均遵循高斯分布；2) 在每个分布中，条件均值都为线性函数，并且协方差恒定。通过以上假设，数据序列的分割问题容易处理且易于扩展。

序列分割问题具体的方法过程如下。首先，使用构建的多元线性模型并结合所给出的变点检测算法计算出变点参数的先验分布以及风险函数；然后，定义出在线分割算法的边界条件；最后，根据初始数据、风险函数和边界条件，推算出分段长度的概率密度函数。3.2.5节将给出具体的分割算法。

3.2.1 变点检测

其中，后验分布为

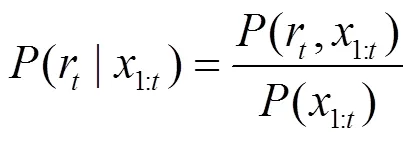
其联合分布就可以递归地表示为

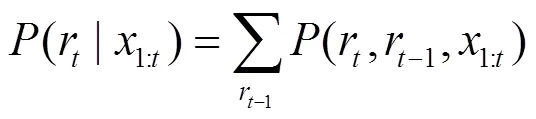
2) 在给定了前一个变点的基础上，可以得出最新数据的预测分布。

3.2.2 风险函数

图1展示的是消息传递算法的过程。其中，圆圈代表运行过程中所有可能的状态；圆圈之间的连线显示的是时间步长之间的递归传递质量；实线表示概率数值正在上升，运行长度在下一个时间段增长；虚线表示当前的运行状态被停止并且数值下降到0的可能性。

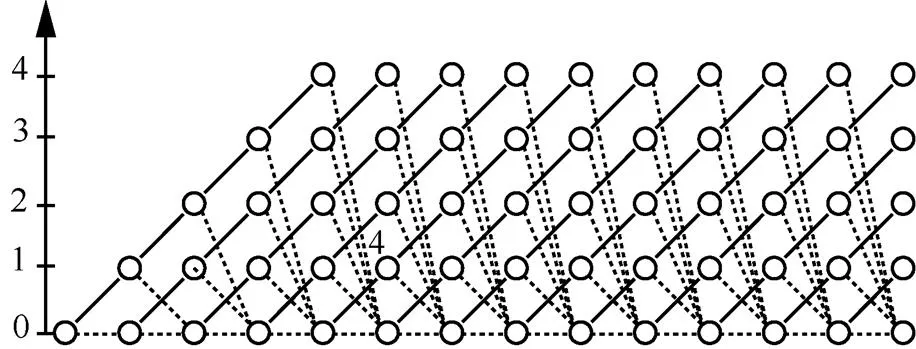
图1 消息传递算法的过程

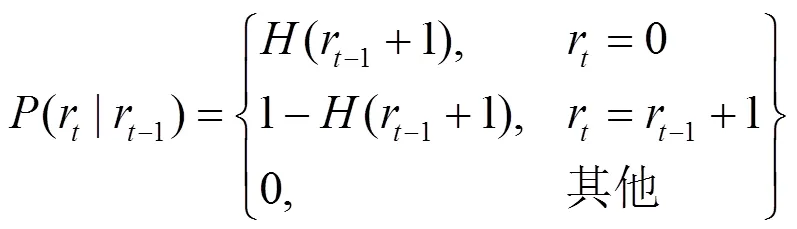
3.2.3 边界条件

通过运行长度的分布函数和观测的数据递归地写出联合分布。递归算法不仅要定义递归关系，还要定义初始化条件，包含以下2种情况。

1) 在第一个基准之前发生变化，例如，在观察数据时，可将初始运行长度的所有概率密度函数重置为0。

2) 更新测试数据发生变化，如在运行长度上升时，根据归一化常数将运行长度重置为0，其数学计算式为

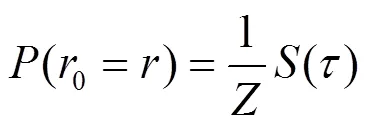
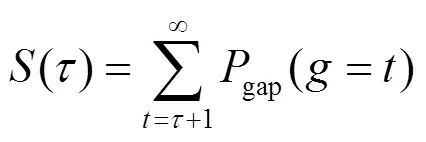
3.2.4 多元线性模型序列分割

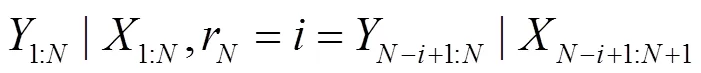
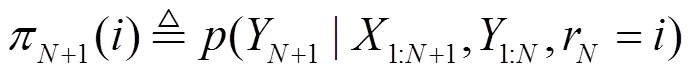
根据式(7)和式(9)可知

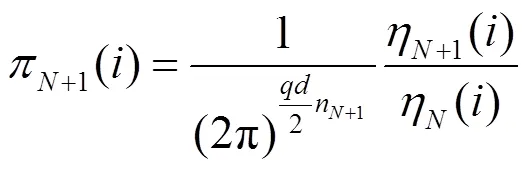
3.2.5 贝叶斯模型分割算法

算法1给出了用于分割数据序列的算法。在该算法中，首先，初始化数据；然后，根据3.2.2节求出的风险函数计算线性分段运行长度的分布函数；接下来更新充分统计量，计算出运行长度边缘预测分布；重复上述过程实现序列分割。

算法1 贝叶斯模型分割算法

1) 初始化

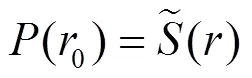
3) 根据式(7)推演后验预测密度函数

4) 根据式(9)计算增长概率密度函数

5) 计算变点密度函数

6) 确定运行长度分布

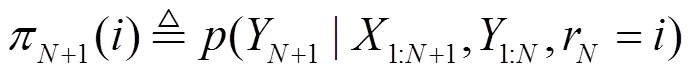
7) 更新充分统计量

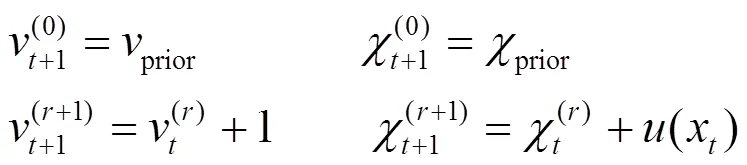
8) 进行预测

9) 重复步骤2)

3.2.6 线性分段粒度分析

3.3 分段聚集与驾驶行为映射

LDA模型也被称为3层贝叶斯概率模型，可以提供方法聚集数据。这些模型常用于文档内容的信息检索，例如，根据每个文档的词汇为该文档指定对应的主题。在本文情况下，文档就是线性分段，而主题是具体的驾驶行为。

与文档中的单词不同的是本文的数据是连续的。为了解决这个问题，本文对传统LDA模型进行了拓展。LDA拓展模型确定主题的过程也是一个分类的过程，具体过程如下，给定驾驶数据序列，使用算法1对数据序列变点进行检测，分割驾驶序列；然后将每个分段当作文档，对其使用LDA拓展模型；根据那些经常出现的词汇归纳出主题，然后可以与语义标签相互关联。

和LDA模型类似，本文给出的LDA拓展模型同样根据线性分段的比例对具体驾驶行为进行预测，同时使用Matlab对该模型进行了验证，结果表明该方法准确性高。

4 离线与在线实验

本节将分别讨论离线实验和在线实验这2种情况下分割和聚集驾驶数据序列的实验结果。首先，收集驾驶数据，利用第3节介绍的方法将实验数据分成近似线性的分段；然后，利用LDA拓展模型聚集线性分段，将其与具体的驾驶行为相映射。

4.1 离线实验

4.1.1 数据的预处理

本文使用惯性传感器来收集驾驶数据。在汽车上利用3轴陀螺仪和线性加速度传感器来测量汽车的惯性数据。传感器被水平地放置在车辆中间位置，轴朝上，轴面向前进方向。在10 min的车程内，平均每秒钟收集5次数据，共收集了超过3 000个数据，如表2所示。

表2 驾驶数据参数

其中，数据预处理涉及提取传感器轴的分割问题。关于轴的旋转被用来作为衡量车辆偏航度，轴的旋转被用来作为衡量测量车辆行驶的坡度，轴的线性加速度被选择为车辆的行驶方向。除了这些针对车辆框架的预处理，该方法唯一的预处理就是消除部分由于传感器不灵敏而收集到的错误的驾驶数据信息。式(21)和式(22)为传感器收集到的数据。

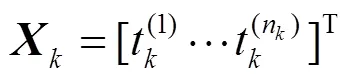
4.1.2 离线驾驶数据分割

整个离线行为分析通过使用算法1中提出的贝叶斯模型分割算法进行序列分割，使用3.3节中提出的LDA拓展模型对线性分段进行聚集。

1) 分段结果

分割算法一共花费11.8 s的时间处理13 m的驾驶数据，平均每个数据花费的时间为86.1 μs，实时性好。共生成170个线性分段，平均每个线性分段持续时间为3.4 s，该数值在3 ~7 s之间变化。

图2所示为120 s内驾驶数据的贝叶斯模型分割算法实验结果，按顺序分别为加速度、轴偏转度、轴偏转度以及线性分段长度随时间的变化。通过变点检测算法，计算出加速度，轴和轴的偏转度数据中的变点，图2(d)中的粗线表示线性分段持续的时间长度，其线性递增，遇到变点归零。通过该实验，成功地检测出驾驶序列中的变点，将驾驶数据序列分割成近线性的分段。

图3(a)为3值航位推测算法的轨迹。该图通过加速度和轴与轴偏转度进行航位推测计算，可以描述车辆的运行轨迹以及道路地形，其中，轨迹上标注的圆圈表示算法计算出的分段边界。可以发现，分段的边界主要集中在拐角和上坡下坡处，直观地说明转弯和爬坡的操作比直线操作更加复杂。

图3(b)为2值平面轨迹，与本文的图3(a)方法相比，缺少轴偏转度（坡度）的数据。在驾驶过程中，地形对驾驶行为的影响是显著的。例如，下坡过程中，就算驾驶员执行滑行的操作，车辆在数据上仍然呈现加速的状态。所以只有消除地形的影响，才能提高聚集数据的精确度。

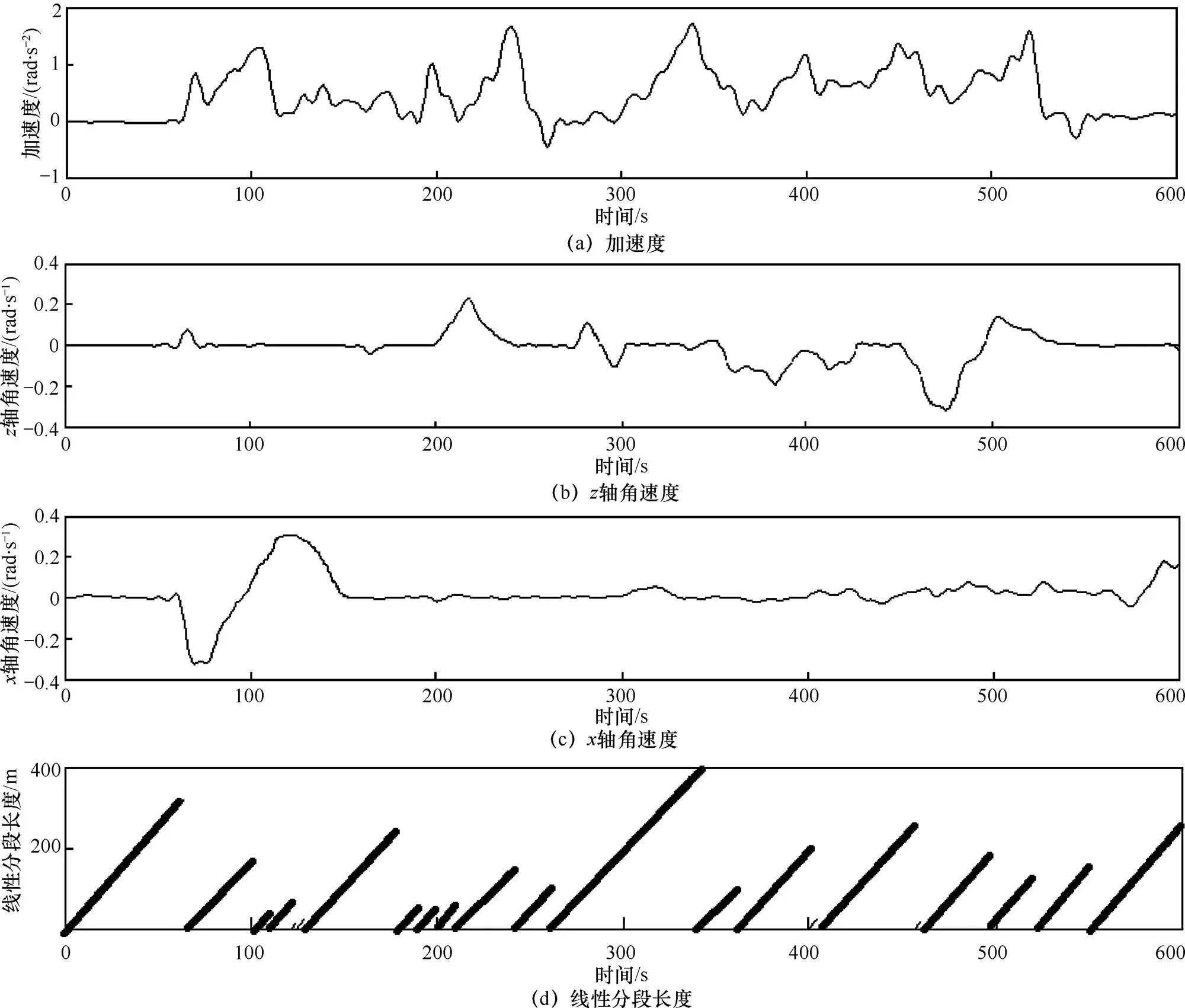
图2 120 s内驾驶数据的贝叶斯模型分割算法实验结果

图3 利用加速度和陀螺仪测量的数据进行的航位推测的轨迹

2) 聚集结果

在完成驾驶序列的线性分割后，使用3.3节提出的LDA拓展模型进行数据聚集。

分段通常由一些不同的主题组成，就像文档通常包含几个不同的主题。本文提出的LDA拓展模型得到分段数据后返回的是每个分段的主题比例，因此可以得出每个文档中有多少主题。其中，5个主题模型的比例如图4所示。

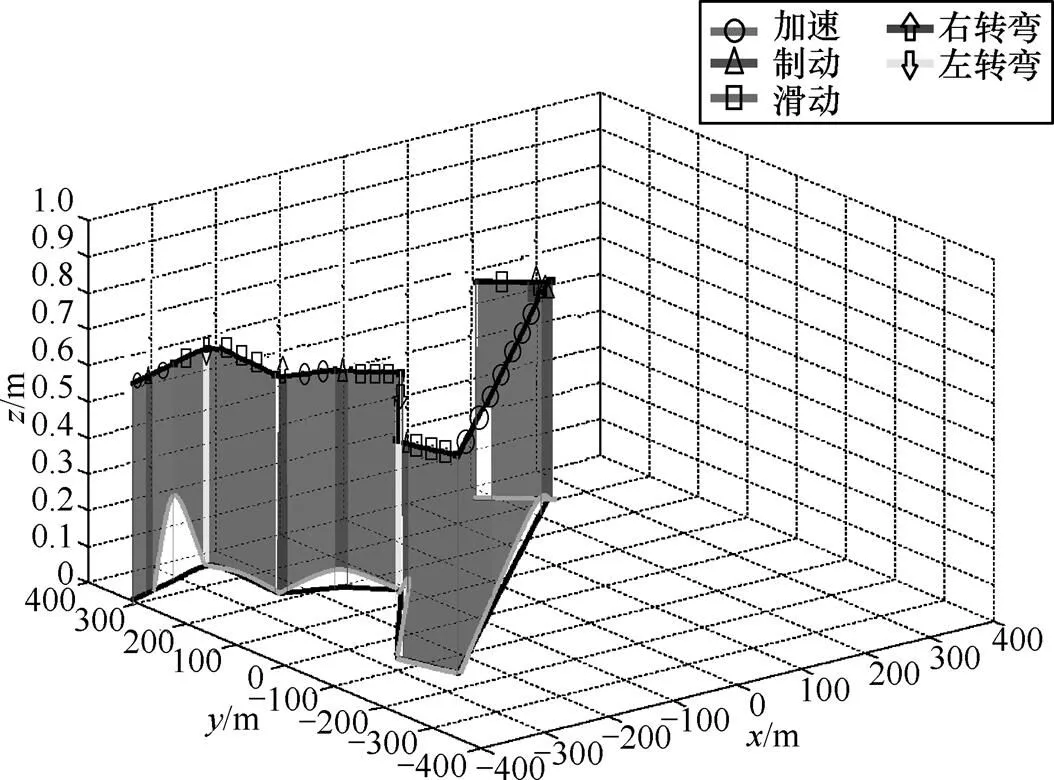
图4 按主题绘线的航位轨迹推算

图4为按主题绘线的航位推测轨迹。每一条线对应着一个分段，其线段图形是5个基本图形的凸组合，每个主题对应一种图形。凸组合中的系数就是主题的比例，而主题是由扩展LDA模型进行选择和分配的。然后可以以直观驾驶行为（如滑行、制动和转向的方式）来标注分段。

图5是对LDA模型聚集法与简单的阈值方法所得出结果进行比较。用于表示阈值数据的规则如下

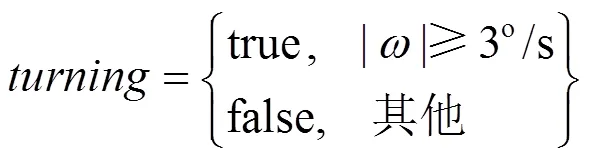
为了降低阈值输出中的噪声，惯性数据使用的是20个样本数据的平均值。

图5展示的是由测试车辆经过2个十字路口执行转弯操作时收集到的惯性数据。车辆以稳定的速度朝向路口行驶，制动减速完成右转弯，然后回到正常速度。再次执行同样的操作，完成左转弯。其中阈值法很容易受到噪声数据的影响。只有对数据进行除噪和调整阈值的级别才能获得理想的结果。但即使有微调，结果仍然容易受到阈值附近的噪声影响。这将导致驾驶数据出现从一个驾驶状态到另一个驾驶状态不正常的快速波动。由图5(b)可以发现，当= 283 s和= 405 s左右时驾驶行为出现快速变动。

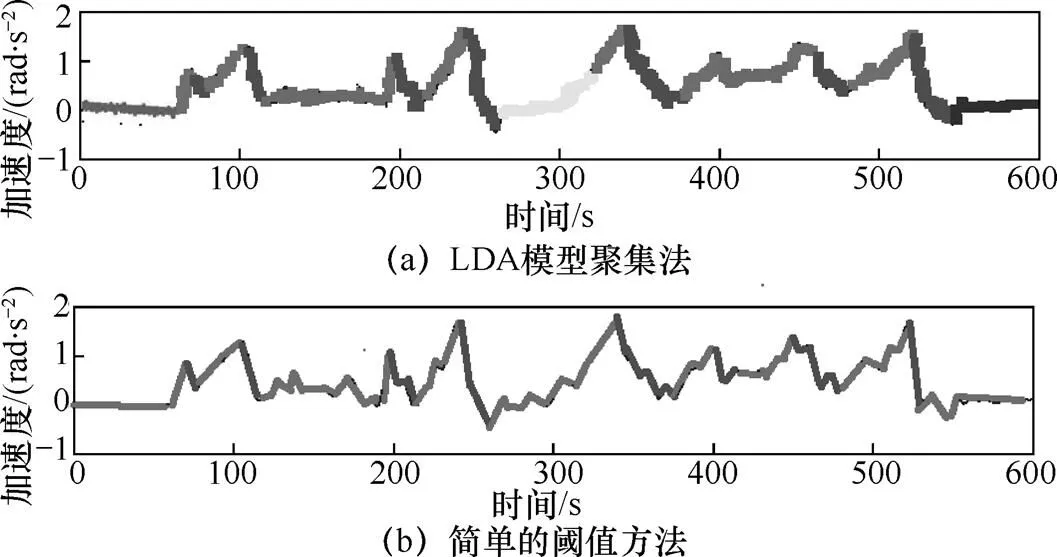
图5 LDA模型聚集法与简单的阈值方法结果比较

由于阈值法严格的规范，导致其提供的简单规则无法正确地模拟局部数据变化对应的主题，例如，在= 283 s到转向加速的过程中，可以发现使用阈值法处理确定驾驶数据分段更加单一。而在这个过程中，本文提供的方法对局部数据处理时生成了更加详细的分段。即使数据的复杂性增加，添加新的规则变得越加困难，该方法还可以进行扩展。只需要添加新数据或增加检测行为的数量，不需要对该模型本身进行其他的修改。

4.2 在线实验

图6和图7分别为在线实验轨迹与校园实验轨迹。本文的在线实验是通过惯性传感器进行驾驶数据的收集，然后利用手机4G网络即时传输到云平台进行计算。云平台通过运行算法1提出的分割算法和3.3节提出的分类方法，将其轨迹图分段以路径的形式显示出来。图6显示的4个图分别对应4个时间段内通过分割和聚集算法推算出的轨迹，图中图形与驾驶行为主题相对应，图中的条形图表示的是在当前驾驶数据情况下的所有主题的后验概率，根据后验概率确定当前主题。图7显示的是根据不同的主题对车辆轨迹进行图形编码的轨迹。可以发现，图6与图7的部分轨迹一致。实验表明，在对应时间内，后验概率最高的驾驶行为主题与观察到的驾驶员正在执行的驾驶行为一致。

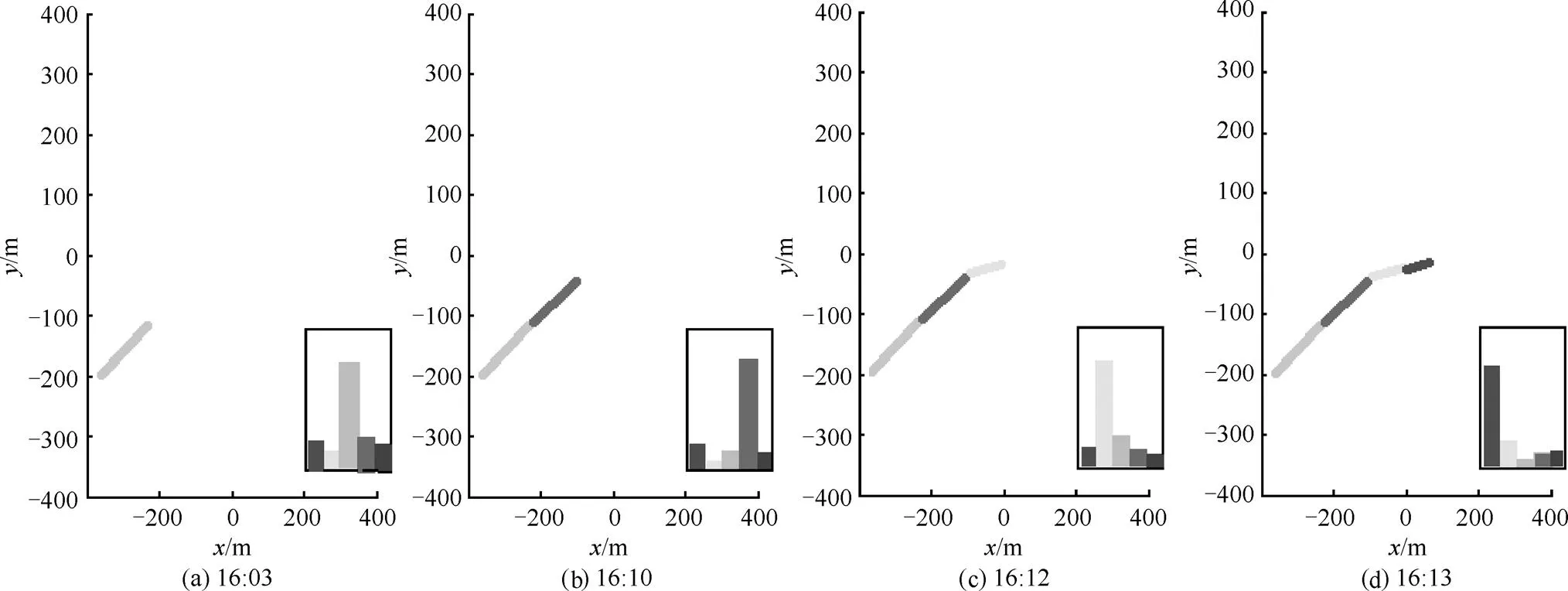
图6 在线实验轨迹

图7 校园实验轨迹

此外，根据在线实验的结果，可以预测三角形线段区域多的路口交通状况不好，因为三角形线段区域多表明车辆多次减速，可见其路况不是很好。下一步的工作是进一步分析图形背后包含的现实含义。

5 结束语

本文提出了识别和预测驾驶行为的方法，实现了如何将分段聚集到与具体驾驶行为相对应的主题中，从而获得有意义的数据。同时，还展示了在线进行分段和聚集。该方法是完全无监管的，而且只需很少的预处理。本文贡献主要有以下3点。

1) 对贝叶斯先验参数进行改进，考虑参数为非零和非对角矩阵的情况，与传统的假设参数为0和对角矩阵相比，算法适用性更高、更可靠。

2) 对LDA模型进行拓展，使用该模型对数据进行聚集，摆脱了传统的阈值带来的决定是肯定或否定，结果以概率的形式显示。同时考虑了道路坡度对驾驶数据的影响，避免因为路况而影响结果的准确性。准确性和适用性较一般算法更好。

3) 通过大量仿真实验验证了所提出的基于贝叶斯模型的算法优于传统算法，从实验结果上可以看出，本文方法结果准确性更高，特别是在道路状况复杂的区域。

未来的研究将进一步考虑道路环境等问题，由于实验条件和算法只允许考虑惯性传感器收集到的数据，在道路环境部分只考虑坡度这一因素，未来将在模型中加入其他道路环境因素，进一步提升算法的适用范围。此外，本文只是识别和预测出驾驶员具体的驾驶行为，但是这些行为背后包含的规律还有待进一步的研究。

[1] FRANKE U, PFEIFFER D, RABE C, et al. Making bertha see[C]// IEEE International Conference on Computer Vision Workshops. 2014: 214-221.

[2] WINNER H, HAKULI S, LOTZ F, et al. Handbook of driver assistance systems: basic information, components and systems for active safety and comfort[M]. Springer Publishing Company, Incorporated, 2015.

[3] CHEN Y, JIANG X H, LIAO L C, et al. Driving behavior motivation model research based on vehicle trajectory data[C]//International Conference on Smart Vehicular Technology, Transportation, Communication and Applications. 2017: 36-44.

[4] DOSHI A, MORRIS B, TRIVEDI M. On-road prediction of driver’s intent with multimodal sensory cues[J]. IEEE Pervasive Computing, 2011, 10(3):22-34.

[5] SATZODA R K, MARTIN S, LY M V, et al. Towards automated drive analysis: a multimodal synergistic approach[C]//International IEEE Conference on Intelligent Transportation Systems. 2013: 1912-1916.

[6] STUBING H, BECHLER M, HEUSSNER D, et al. SIM TD : a car-to-X system architecture for field operational tests[J]. IEEE Communications Magazine, 2010, 48(5):148-154.

[7] ALEXANDER P, HALEY D, GRANT A. Cooperative intelligent transport systems: 5.9-GHz field trials[J]. Proceedings of the IEEE, 2011, 99(7):1213-1235.

[8] LI Z, BAO S, KOLMANOVSKY I V, et al. Visual-manual distraction detection using driving performance indicators with naturalistic driving data[J]. IEEE Transactions on Intelligent Transportation Systems, 2017, PP(99):1-8.

[9] MAYE J, TRIEBEL R, SPINELLO L, et al. Bayesian on-line learning of driving behaviors[C]//IEEE International Conference on Robotics and Automation. 2011:4341-4346.

[10] YAN X, SU X G. Bayesian linear regression[J]. Security Ticket Control, 2009, 15(1):1052-1056.

[11] KIRCHNER M R, RYAN K, WRIGHT N. Maneuvering vehicle tracking with Bayesian changepoint detection[C]// IEEE Aerospace Conference. 2017:1-9.

[12] KRESTEL R, FANKHAUSER P, NEJDL W. Latent dirichlet allocation for tag recommendation[C]//ACM Conference on Recommender Systems. 2009: 61-68.

[13] HARLÉ F, CHATELAIN F, GOUY-PAILLER C, et al. Bayesian model for multiple change-points detection in multivariate time series[J]. IEEE Transactions on Signal Processing, 2016, 64(16):4351-4362.

[14] KIM J H, HAYAKAWA S, SUZUKI T, et al. Modeling of driver's collision avoidance maneuver based on controller switching model[J]. IEEE Transactions on Systems Man & Cybernetics Part B Cybernetics, 2005, 35(6):1131-1143.

[15] SEKIZAWA S, INAGAKI S, SUZUKI T, et al. Modeling and recognition of driving behavior based on stochastic switched ARX model[C]//IEEE Conference on Decision and Control, 2005 and 2005 European Control Conference. 2006: 5095-5100.

[16] TERADA R, OKUDA H, SUZUKI T, et al. Multi-scale driving behavior modeling using hierarchical PWARX model[C]//International IEEE Conference on Intelligent Transportation Systems. 2010: 1638-1644.

[17] TANIGUCHI T, NAGASAKA S, HITOMI K, et al. Semiotic prediction of driving behavior using unsupervised double articulation analyzer[C]//Intelligent Vehicles Symposium. 1931:849-854.

[18] BANDO T, TAKENAKA K, NAGASAKA S, et al. Unsupervised drive topic finding from driving behavioral data[C]//Intelligent Vehicles Symposium. 2013:177-182.

[19] JOHNSON D A, TRIVEDI M M. Driving style recognition using a smartphone as a sensor platform[C]//International IEEE Conference on Intelligent Transportation Systems. 2011:1609-1615.

[20] PAUL F, ZHEN L. On-line inference for multiple changepoint problems[J]. Journal of the Royal Statistical Society, 2007, 69(4):589-605.

[21] LY M V, MARTIN S, TRIVEDI M M. Driver classification and driving style recognition using inertial sensors[C]//Intelligent Vehicles Symposium. 2013:1040-1045.

[22] MAYE J, TRIEBEL R, SPINELLO L, et al. Bayesian on-line learning of driving behaviors[C]//IEEE International Conference on Robotics and Automation. 2011:4341-4346.

[23] STEPHENS D A. Bayesian retrospective multiple-changepoint identification[J]. Journal of the Royal Statistical Society, 1994, 43(1): 159-178.

Driving behavior recognition and predictionbased on Bayesian model

WANG Xinsheng, BIAN Zhen

School of Computer Science and Communication Engineering, Jiangsu University, Zhenjiang 212013, China

Since the existing intelligent driving systems are lack of efficiency and accuracy when processing huge number of driving data, a brand new approach of processing driving data was developed to identify and predicate human driving behavior based on Bayesian model. The approach was proposed to take two steps to deduce the specific driving behavior from driving data correspondingly without any supervision, the first step being using Bayesian model segmentation algorithm to divide driving data that inertial sensor collected into near-linear segments with the help of Bayesian model segmentation algorithm, and the second step being using extended LDA model to aggregate those linear segments into specific driving behavior (such as braking, turning, acceleration and coasting). Both offline and online experiments are conducted to verify this approach and it turns out that approach has higher efficiency and recognition accuracy when dealing with numerous driving data.

driving data, Bayesian model, inertial sensor, linear segmentation

TP393

10.11959/j.issn.1000-436x.2018043

2017-10-25；

2018-02-10

国家自然科学基金资助项目（No.U1764263）

The National Natural Science Foundation of China (No.U1764263)

王新胜（1972-），男，江苏宿迁人，博士，江苏大学副教授，主要研究方向为无线传感器网络等。