ARX模型组在四旋翼飞行器建模中的应用

刘丽丽　左继红　吴　军

（1.湖南铁道职业技术学院　株洲　412001）（2.长沙理工大学电气与信息工程学院　长沙　410083）

1　引言

近年来四旋翼飞行器在航拍、侦察、勘探和监控等方面应用广泛［1］。但是四旋翼飞行器是一个典型的多变量、非线性、强耦合和欠驱动的系统，使得控制变得复杂。文献［2～5］采取线性控制策略进行解耦控制，但在非平衡工作点处无法使系统保持稳定状态。文献［6～8］采用滑模控制策略进行系统控制，但需要不断切换工作区间，造成系统抖动，控制效果不理想。文献［9～11］采取反步法设计控制器，但是该法对模型的精确性有较高要求。本文从飞行器系统的非线性出发，采取ARX建模理论建立系统的ARX模型组，基于此模型设计了自适应LQR（linear-quadratic regulator）控制策略来控制四旋翼飞行器的姿态和位置。通过仿真与实时控制实验，证实该法控制效果优良，能使系统在较短时间内达到稳定。

2　四旋翼飞行器本体介绍

本文所采用的四旋翼飞行器实验平台如图1所示［12］，它可以用来检验建模和控制方法在四旋翼飞行器中的使用效果。为降低控制的难度及延长飞行器的使用寿命，固定其三个自由度，重点研究其姿态控制。姿态控制包括飞行器的前进后退和左右平移，对于飞行器系统来说至关重要。从图中可看出，3个旋翼水平安装，它们决定了飞行器的俯仰和翻转姿态，还有一个竖直安装，决定了飞行器的巡航方向。故该系统有3个输出4个输入。输出分别是翻转角、俯仰角和巡航角，输入分别是旋翼上四个电机的电压。

图1　四旋翼飞行器实验平台

3　ARX模型组建模

3.1　ARX模型建模

ARX建模理论［13］多用于系统的线性建模，对于非线性系统，可采用一组ARX模型进行描述。将全局工作区分为若干区间，每个区间可采用一个ARX模型进行描述其动态特性，整个工作区的非线性动态特性就可以采取一组ARX模型进行描述。四旋翼飞行器的俯仰角和翻转角决定其姿态，飞行姿态体现了非线性特征。故依据俯仰角和翻转角的工作区间范围，根据式（1）将系统的全局工作区平均划分为16个区间

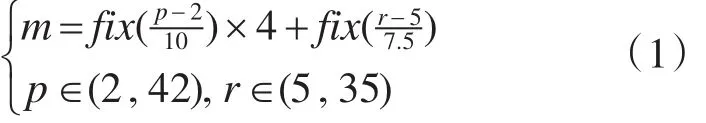
其中m代表区间号，fix（）代表取整函数。俯仰角范围从2°～42°，通过取整函数可以均衡划分4个工作区间，翻转角范围从5°～35°，通过取整函数也可以划分成4个区间，这些区域相互交叉，可以组成16个区间。如当p=32，r=20时，区间号m=14。

在每个工作区间，采取ARX建模理论进行建模，并辨识出参数得到局部ARX模型。这些局部区间模型结构相同，辨识方法也相同，任一局部线性模型按照下述方法进行建模。

对于4输入3输出的四旋翼飞行器，其局部线性ARX模型为

其中Y(t)=[p(t)r(t)y(t)]T代表输出俯仰角、翻转角和巡航角，输入u(t)=[Vf(t)Vr(t)Vl(t)Vb(t)]T表示四个电机电压，na、nb和d表示模型阶次，e(t)表示建模误差，系数矩阵Ak和Bk为

设某一状态下输出和输入分别是Ys和Us。则模型（2）可转换为模型：

则模型（4）可转换为状态模型［14］：

3.2　模型辨识

模型阶次的确定有多种方法，如损失函数法、Akaike法和AIC准则等。这里采用AIC准则［15］来计算模型阶次，计算公式如下

其中N代表数据的长度，||Σ代表模型残差协方差矩阵的行列式。

采集物理模型下飞行器系统运行数据，做为辨识模型的数据。四旋翼飞行器模型组中每个局部模型的辨识过程一样。使飞行器稳定运行在一工作区间，在此基础上加一白噪声信号，使飞行器摆动体现动态非线性特性。并釆集此时输入输出数据，作为模型辨识数据。

采用最小二乘法辨识模型参数，不同阶次下，计算出模型的AIC值。综合权衡AIC值和实控效果，确定模型阶次为na=3，nb=1，d=2 。

3.3　模型输出结果分析

以工作区间号11为例，图2～图4是飞行器运行在该区间内，它的三个输出（俯仰角、翻转角和巡航角）的ARX模型输出与系统实际输出间的对比情况。

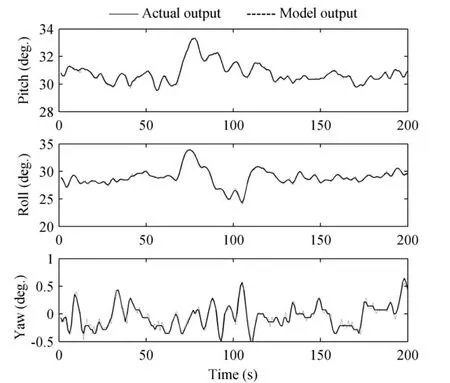
图2　ARX模型输出与实际输出对比

图2～图4表明，俯仰角在30°～34°之间波动，误差分布在-0.2mm～0.2mm之间，翻转角在25°～35°之间波动，误差分布在-0.4mm～0.4mm之间，巡航角在-0.5°～0.5°之间波动，误差在-0.1mm～0.2mm之间，整体来看模型输出误差相对比较小，误差的分布类似白噪声，模型能够较好反映飞行器系统局部动态特征。依据同样的建模及辨识方法，可以得到全部工作区间内的模型，从而达到建立全局模型的目的。

图3　ARX模型输出误差图

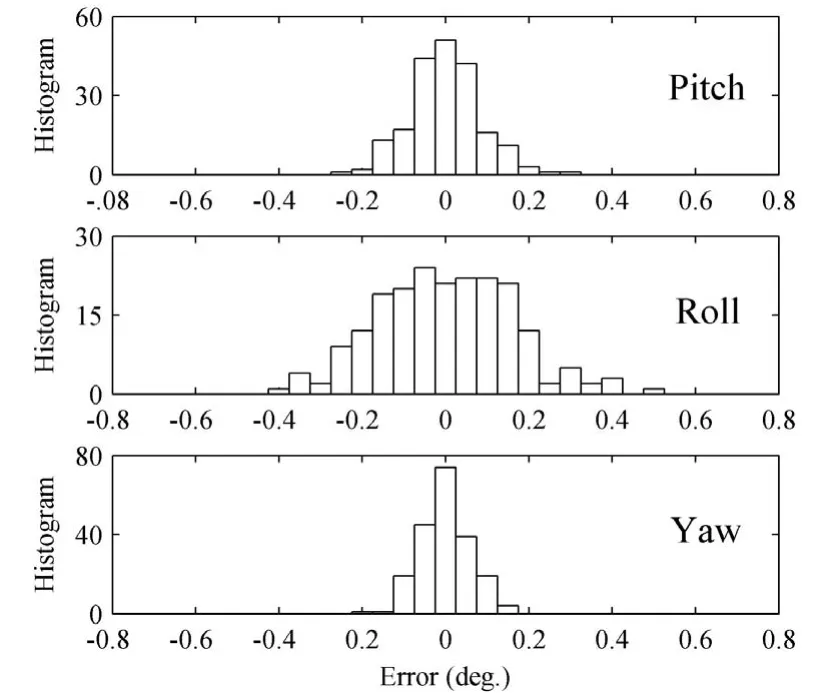
图4　模型输出误差直方图

为进一步验证模型的精确性，可以局部放大某工作区间内ARX模型预测输出与系统实际输出，分析误差分布。图5～7分别表示四旋翼飞行器俯仰角、翻转角和巡航角的ARX模型输出与实际输出情况。从图中可以看出系统的模型输出能很好跟踪系统的实际输出，模型拟合精度较高，能较好描述系统的非线性特性。

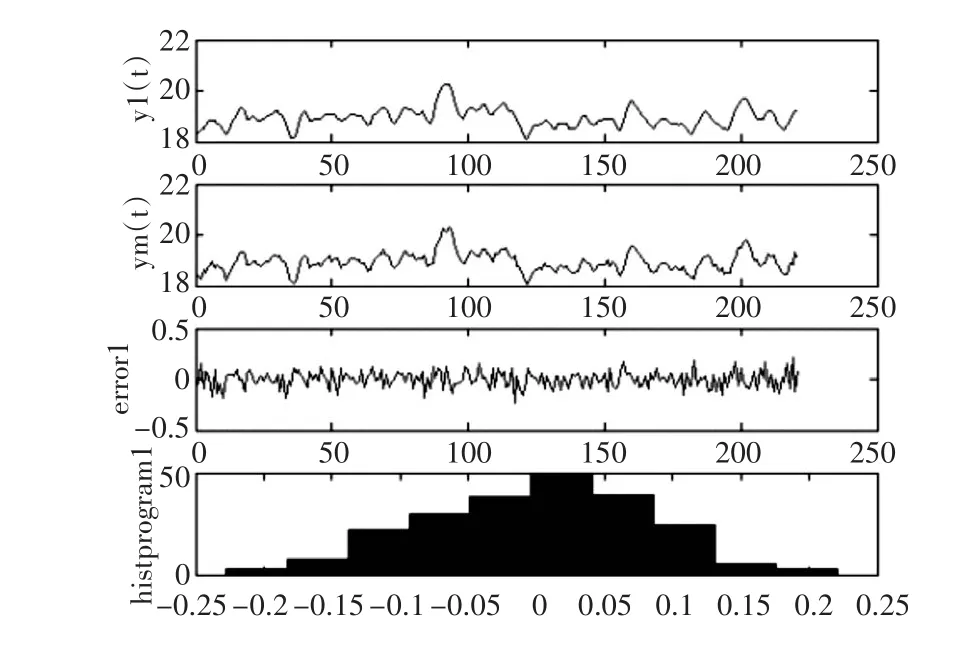
图5　俯仰角两者输出对比（y1（t）代表实际输出，ym1（t）代表模型输出）

图6　翻转角两者输出比较（y2（t）代表实际输出，ym2（t）代表模型输出）

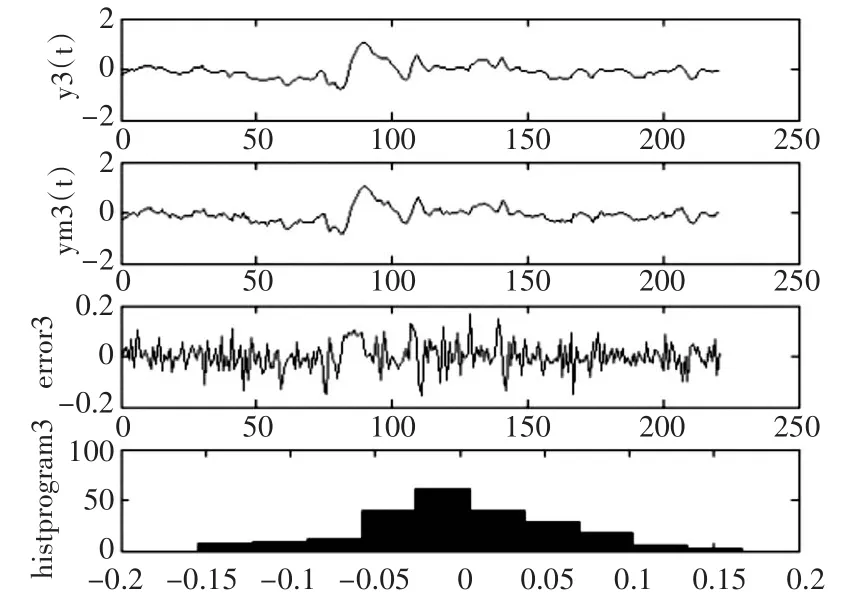
图7　巡航角两者输出比较（y3（t）为实际输出，ym3（t）为模型输出）

4　结语

针对具有较强非线性和耦合的四旋翼飞行器系统，采用一种新型ARX模型对其进行建模，详述了辨识模型参数的方法，通过模型预测输出仿真结果观察建模精度，结果显示该建模方法具有较高的建模精度，模型能很好描述系统全局非线性特征。

［1］Fu J，ChaiTY，Su CY，etal.Motion/force Tracking Control of Nonholonomic Mechanical Systems via Combining Cascaded Design and Backstepping［J］.Automatica，2013，49（12）：3682-3686.

［2］Bresciani T.Modelling，Identification and Control of a Quadrotor Helicopter［D］.Lund：Lund University，2008.

［3］Saif A，Hiddabi A.Quadrotor Control Using Feedback Linearization with Dynamic Extension［C］.Proceeding of the 6th International Symposium on Mechatronics and its Applications，Sharjah，2009.

［4］Altug E，Erginer B.Modeling and PD Control of a Quadrotor VTOL Vehicle［C］//IEEE International Conferance on Vehicles Symposium，Istanbul，2007.

［5］ Bouabdallah S，Siegwart R.Backstepping and Sliding-mode Techniques Applied to an Indoor Micro-quadrotor［C］//Proceeding of the IEEE International Conference on Roboticsand Automation，Barcelona，2005.

［6］González Iván，Sergio Salazar，Rogelio Lozano.Chattering-Free Sliding Mode Altitude Control for a Quad-Rotor Aircraft：Real-Time Application［J］.Journalof Intelligent&Robotic Systems，2013，73（1-4）：1-19.

［7］Tan L N，Lu L B，Jin G D.Attitude Stabilization Control of a Quadrotor Helicopter Using Integral Backstepping［C］//Automatic Control and Artificial Intelligence（ACAI 2012），2012.

［8］McKerrow P.Modelling the Draganflyer four-rotor helicopter［C］//IEEE International Conference on Robotics and Automation，4，2004.

［9］Bouabdallah S，Noth A，Siegwart R.PID vs LQ Control Techniques Applied to an Indoor MicroQuadrotor［C］//IEEE International Conference on Intelligent Robots and Systems，2004.

［10］ Bouabdallah S，Siegwart R.Backstepping and Sliding-mode Techniques Applied to an indoorMicroQuadrotor［C］//International Conference on Robotics and Automation，Barcelona，2005.

［11］ Scott D.Hanford.A Small Semi-autonomous Rotary-wing Unmanned Air Vehicle［D］.U-niversity of Pennsylvania，2005.

［12］GOOGOL TECHNOLOGY LTD，“the manual of the quadrotor simulator”

［13］HuiPeng，Tohru Ozaki，Yukihiro Toyoda，Hideo Shioya，Kazushi Nakano， Valerie Haggan-Ozaki， Massafumi Mori.RBF-ARX model-based nonlinear system modeling and predictive controlwith application to a decomposition process［J］.Control Engineering Practice，12（2004）：191-203.

［14］徐仲，张凯院，陆全，等.矩阵论简明教程［M］.北京：科学出版社，2001.145-151.XU Zhong，ZHANG Kaiyuan，LU Quan，etal.Introductory tutorial matrix theory［M］.Beijing：science press，2001.145-151.

［15］秦宣云，卜英勇，夏毅敏.基于AIC准则优化的径向神经网络微地形曲面重构［J］.中南大学学报（自然科学版），2004，35（5）：815-819.QIN Xuanyun，BU Yingyong，XIA Yimin.Radial neural network based on AIC criterion optimization tiny terrain surface reconstruction［J］.Journal of central south university（naturalscience edition），2004，35（5）：815-819.