衰减记忆平方根容积卡尔曼滤波及其应用

杨旺明

（三峡大学　宜昌　443002）

1　引言

目标跟踪技术是信号处理领域的一个重要研究方向，有着极为广泛的应用价值。随着现代信号处理技术的发展，目标的机动能力大幅提高，光电跟踪系统中原有的采用标准卡尔曼滤波对目标进行跟踪和预测的方法，显然已越来越难以满足目标跟踪精度和预测精度的要求［1］。

光电跟踪系统中的目标跟踪属于非线性估计问题，解决该问题常用的非线性方法有粒子滤波（PF）算法、扩展卡尔曼滤波（EKF）算法和无迹卡尔曼滤波（UKF）算法等［2～3］。PF算法由于计算较为复杂，实时性较差，很少应用于要求快速反应的实际工程中；EKF算法是传统非线性状态估计的代表，但只适用于弱非线性系统，对于强非线性系统，存在着滤波精度不高，稳定性差，以及在高维情况下计算较为复杂等缺点［4］；UKF算法利用一组sigma点代表状态变量的分布，并以此求解非线性系统高斯随机变量的均值和方差，对于任何的非线性系统精度都能达到二阶以上［5］，其精度高于EKF。文献［6］中提出的CKF算法是一种基于容积数值积分准则的递推型贝叶斯滤波器，该算法具有优越的非线性逼近性能、数值精度以及滤波稳定性，又不必预先设定参量，易于实现，因而得到广泛应用［7～9］。在实际的滤波过程中，由于计算机字长有限，因而存在着计算误差，这些误差积累起来，会降低滤波精度，甚至造成计算发散；在目标跟踪中，不可能完全获悉目标的运动状态，因此不能真实反映物理过程，使得观测值与模型不匹配，会造成滤波发散。为了提高CKF算法的精度和稳定性，文献［4］提出了SCKF算法，以估计误差的平方根矩阵进行迭代计算，解决了CKF算法中由于计算误差引起的计算发散问题，但并未解决由模型误差引起的滤波发散问题。

因此，本文应用衰减记忆滤波算法对SCKF算法进行改进，提出了MASCKF算法，以克服由模型误差引起的滤波发散，提高滤波精度和稳定性。最后，仿真验证了该算法的有效性。

2　MASCKF算法

2.1　容积积分原理

离散非线性动态系统的状态方程为

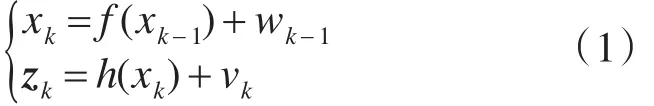
式中，xk为系统状态估计向量；zk为量测值；过程噪声 wk-1和量测噪声 vk相互独立，且 wk-1~N(0，Qk-1)，vk~N(0，Rk)。

SCKF算法将非线性滤波归结为非线性函数与高斯概率密度乘积的积分求解问题，即

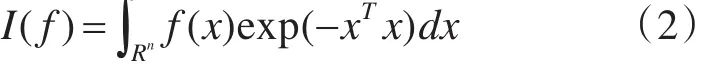
式中，I(f)为所求积分；x为状态估计向量；f(x)为求积非线性函数；Rn为积分域。

对于式（14）的积分问题，SCKF算法采用Spherical-Radial求容积规则，采用一组2n个等权值的容积点来实现非线性逼近，即

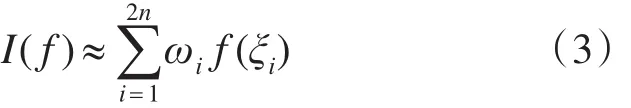
式中，n为状态变量维数。

使用三阶容积原则获得的基本容积点和对应权值为

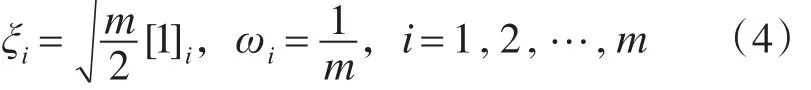
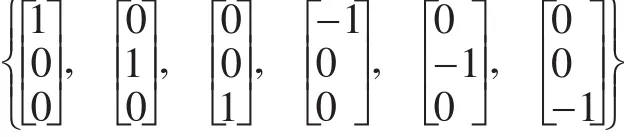
SCKF具体算法可参考文献［6］。

2.2 MASCKF算法

显然，SCKF对观测数据的记忆是无限增长的，即计算k时刻的最优估计 x̂k|k时要用到k时刻以前所有的观测数据。因此，当滤波模型不准确时，随着k的增大，滤波值中的旧数据比重太大，新数据由于比重太小而不能有效抑制误差对状态估计的影响，易引起滤波发散。因此，逐渐减少旧数据的权重，相对地增加新数据的权重，是克服由模型误差引起的滤波发散的有效方法［10］。根据这一观点设计的滤波方法被称为衰减记忆滤波。本文在SCKF算法的基础上引入衰减记忆滤波思想，设计了MASCKF算法。

为了克服N时刻的滤波发散，就应该相对突出增益WN，而相对减小N时刻以前的增益矩阵Wk，且Wk与 Rk，Qk-1为负相关关系。所以，为了达到上述目的，可使远离N时刻的Rk，Qk-1逐渐变大。本文采用指数加权法，将…，R处理为下列矩阵：

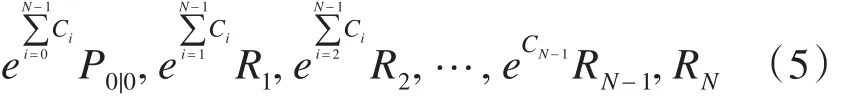
式中，Ci(i=0，1，2，…)是适当选取的正整数。

同样地，将N时刻以前的系统噪声的作用逐渐衰减，则有

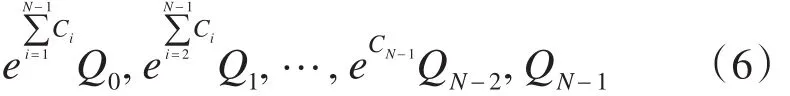
因此，在式（1）过程噪声wk-1和量测噪声vk的分布变为

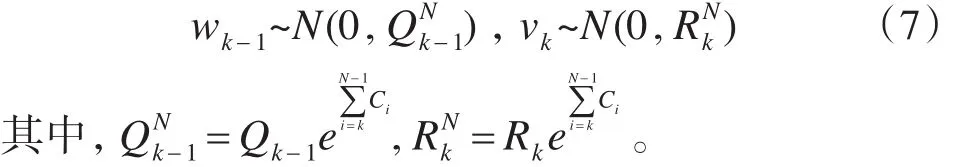
1）时间更新

采用Cholesky方法分解协方差：

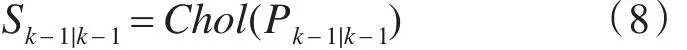
计算容积点：

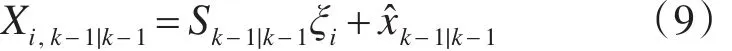
式中 i=1，2，3，…，M。

计算通过状态方程传播的容积点：

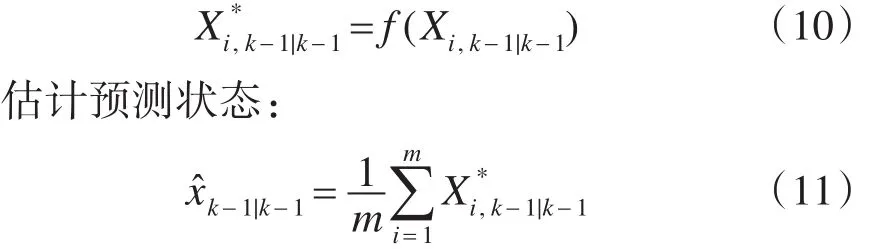
估计预测误差方差矩阵的平方根：在实际应用中，当系统模型描述不准确及噪声统计特性不确定时，新数据对预测值的修正作用下降，旧数据的修正作用相对上升，滤波误差的均值趋于无穷大产生发散现象。综上所述，从滤波发散的原因入手，取Ci＞0时，衰减因子提高了新数据的权值。与常规SCKF算法相比，衰减记忆容积卡尔曼滤波算法在式（13～14）中增加了一个衰减因子，加重当前时刻数据在状态估计中的作用，从而避免滤波器发散。

3　光电跟踪中的目标状态估计

由于光电跟踪的目标量测信息是在极坐标系中得到的，如果将其转化为直坐标系的位置信息，量测信息将在数学转换中失去物理量测之间的不相关性，使滤波效果变差［11］。因此，本文直接在极坐标系中进行滤波预测。为了检验所设计算法在目标模型不准确条件下的对滤波精度的改善效果，目标模型直接采用三阶常加速（CA）模型。

以跟踪目标在俯仰平面上的角度滤波预测为例，选取目标俯仰角位移、角速度和角加速度作为状态变量，即

4　仿真实验及结果分析

4.1　仿真条件设定

实际光电跟踪系统的目标俯仰角滤波中，滤波输入信号为目标相对于跟踪平台的俯仰角度值，即跟踪平台的高低指向和量测所得的脱靶量信号值之和。本文为了验证MASCKF算法在目标模型不准确的条件下对滤波性能的改善，特将正弦信号θ(t)=sin(0.628t)rad作为所跟踪的目标在水平方位上的角位移，则θ(t)即为跟踪系统方位角跟踪的等效正弦输入信号。量测系统的量测间隔为T=0.01s，量测噪声方差为Rk=1.8m rad，系统噪声方差为Qk=25m rad s2。滤波状态初值选为 x0=[0，0，0]T，误差协方差的初值为：P0|0=diag[1000，1000，1000]。选用CKF算法和SCKF算法作为参照对比实验。

4.2　仿真试验结果分析

在上述条件设置下，以θ(t)为等效正弦输入信号，分别用MASCKF、CKF和SCKF方法进行100次蒙特卡罗方法仿真，三种滤波算法预测的位移、速度和加速度的均方根误差如图1、2、3所示。

由图1、2、3可知，由于正弦运动是变加速运动，目标模型不可能精确匹配实际情况，所以三种滤波算法预测出的位移、速度和加速度都还存在一些误差；CKF由于受到计算发散和由模型误差引起的滤波发散的影响，其均方根误差值一直较大，且处于剧烈变化中；与CKF相比，SCKF由于采用了平方根方法削弱了计算误差，减小了滤波误差，其结果精确和稳定；而MASCKF算法同时采用了平方根方法和衰减记忆滤波，有效抑制了计算误差和滤波发散，其位移、速度和角速度的均方根误差明显降低，且趋于稳定状态。

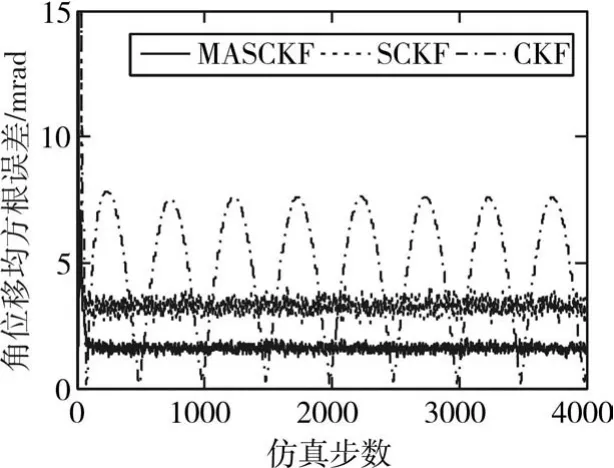
图1　角位移均方根误差

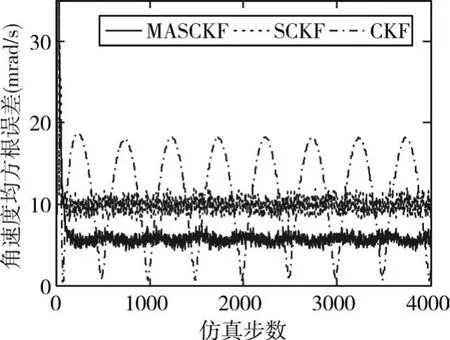
图2　角速度均方根误差

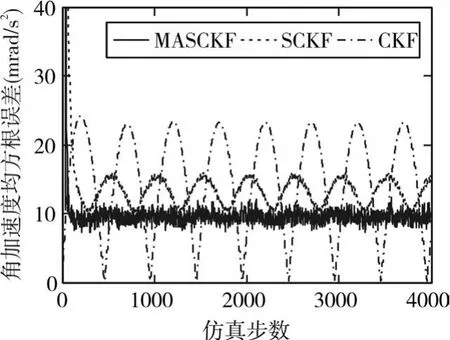
图3　角加速度均方根误差

5　结语

CKF算法由于其推理严谨、易于实现而得到广泛应用。但CKF属于卡尔曼滤波框架的滤波算法，因而同样面临着由计算误差带来的计算发散和由系统的模型误差引起的滤波发散。采用平方根方法改善CKF的SCKF算法只能有效抑制计算发散，因此，本文在SCKF算法基础上应用衰减记忆滤波算法对其进行改进，提出了MASCKF算法，以克服由模型误差引起的滤波发散，提高滤波精度。并将此方法应用到光电跟踪系统的目标跟踪滤波预测中，通过仿真对比表明，在目标运动模型不准确的条件下，MASCKF的滤波精度和稳定性优于SCKF和CKF。

［1］李文军，陈涛.基于卡尔曼滤波器的等效复合控制技术研究［J］.光学精密工程，2006，14（2）：279-284.LIWenjun，CHEN Tao.Equivalentcombined control technique based on Kalman filter.Optics and Precision Engineering，2006，14（2）：279-284.

［2］Sun F C，Hu X S，Zou Y，et al.Adaptive unscented Kalman filtering for state of charge estimation ofa lithium-ion batteryfor electricvehicles［J］.Energy，36 （5） ：3531-3540.

［3］Yang X J，Xing K Y，Feng X L.Maneuvering Target Tracking in Dense Clutter Based on Particle Filtering［J］.2011，24（2）：171-180.

［4］付广仁，曹正文，米林山，等.基于最小二乘和EKF的伪卫星定位算法［J］.计算机工程与应用，2012，48（34）：148-151.FU Guangren，CAO Zhengwen，MILinshan，et al.Pseudolite positioning algorithm based on least squares and EKF.Computer Engineering and Applications，2012，48（34）：148-151.

［5］Bruno O S，Leonardo A B，Paulo I，et al.Flight path reconstruction-a comparison of nonlinear Kalman filter and smoother algorithms［J］.Aerospace Science and Technology，2011，15（1）：60-71.

［6］Ienkaran A，Simon H.Cubature Kalman filter［J］.IEEE Trans.on Automatic Control，2009，54（6）：1254-1279.

［7］穆静，蔡远利.迭代容积卡尔曼滤波算法及其应用［J］.系统工程与电子技术，2011，33（7）：1454-1457.MU Jing，CAIYuanli.Iterated cubature Kalman filter and its application.Systems Engineering and Electronics，2011，33（7）：1454-1457.

［8］鹿传国，冯新喜，张迪.基于改进容积卡尔曼滤波的纯方位目标跟踪［J］.系统工程与电子技术，2012，34（1）：28-33.LU Chuanguo，FENG Xinxi，ZHANG Di.Pure bearing tracking based on improved cubature Kalman filter.Systems Engineering and Electronics，2012，34（1）：28-33.

［9］Martin H，Karl J，Jiri J，etal.Dynamicmodeling of neuronal responses in fMRI using cubature Kalman filtering［J］.NeuroImage，2011，56（4）：2109-2128.

［10］朱萍，茅旭初.基于衰减记忆UKF的高精度GPS定位估计［J］.计算机仿真，2011（2）：35-38.ZHU Ping，MAO Xuchu.A High Precision GPSPosition Estimation.Computer Simulation，2011（2）：35-38.