浅谈数学课堂上的历史教育

◎金琳

数学，作为一门基础性学科，一门从小学到大学的必修课，让绝大多数的中职学生望而生畏，数学课堂更是让他们感到枯燥乏味。如何给数学课堂带来生机与活力，是所有数学教师共同探索的课题。

中国，5000年的文明古国，数学一直贯穿在历史的长河里，从仰韶文化时期出土的陶器上面已刻有表示1234的符号，到西安半坡出土的陶瓷有用1～8个圆点组成的等边三角形和分正方形为100个小正方形的图案；从甲骨文中记载的十进制数字和记数法，到由天干地支组成的60个名称来记日期，再到用阴阳符号构成的八卦表示64种事物；从“矩不方，规不可以为圆”，到“一尺之锤，日取其半，万世不竭”。

当数学碰上历史，让历史融入数学，在数学的课堂中，我们探索用历史引起学生的兴趣，用前人的智慧探求今日的新知。

一、勾股定理

勾股定理是学生解决三角形问题的基础，学生从初中接触直角三角形开始就了解了勾股定理，但却不了解其实我国是发现和研究勾股定理最古老的国家之一，因此，我们可以借助勾股定理，让学生了解这段历史，也了解勾股定理名字的由来。

我们古代数学家称直角三角形为勾股形，较短的直角边称为勾，另一直角边称为股，斜边称为弦，所有勾股定理也称为勾股弦定理，这也就是勾股定理名称的由来。

从初中开始，学生就知道了三条边分别为3，4，5可以组成直角三角形，也知道“勾三股四弦五”这一说法，但是对于这一说法的由来，是我们可以让学生进行了解，提高兴趣的所在。在公元前1000多年，据记载，商高（约公元前1120年）答周公曰“故折矩，以为勾广三，股修四，径隅五。既方之，外半其一矩，环而共盘，得成三四五。两矩共长二十有无，是谓积矩。”这就是最早发现的勾股定理的应用。在公元前7至6世纪，中国学者陈子，曾经给出过任意三角形的三边关系：以日下为勾，日高为股，勾、股各乘并开方除之得斜至日。这就是我们最早给出的勾股定理，而在他之后一二百年，希腊的著名数学家毕达哥拉斯发现了这一定理。

而对于勾股定理的证明，课本上早已给出了证明过程，同学们对此也有所了解，而我们需要借此机会给学生展示我国历史上对于勾股定理的证明。

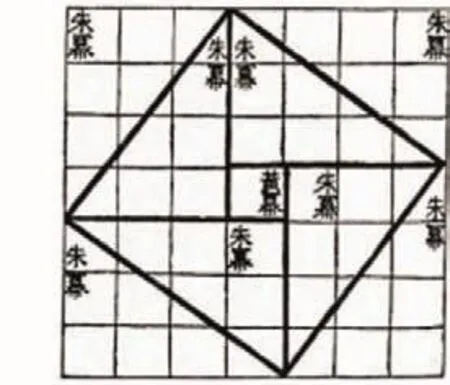
青朱出入图是东汉末年数学家刘徽根据“割补术”运用数形关系证明勾股定理的几何证明法。刘徽描述此图为：“勾自乘为朱方，股自乘为青方，令出入相补，各从其类，因就其余不动也，合成弦方之幂。开方除之，即弦也。”三国时期赵爽为证明勾股定理作“勾股圆方图”即“弦图”，为东方特色勾股定理无字证明法。

由此，我们不仅让同学们了解的勾股定理的由来，对于勾股定理的证明也有所了解，更对于中国古代数学在勾股定理方面的历史有所了解。

二、杨辉三角

在《二项式定理》这一节的内容里，我们提出了杨辉三角这个概念，而杨辉三角其实曾经出现在同学们从小学开始做的找规律的题目中，但是对于杨辉三角这一说法是现在提出的，在传统的课堂中，杨辉三角这个名称我们往往一笔带过，使得同学们对它只是有一个印象，甚至有部分同学过后就连名字也忘了。在中职数学课堂中，我们可以借助讲述杨辉三角的由来，引起同学们的注意，提高同学们的兴趣，从而也让同学们对于中国的历史有所了解。

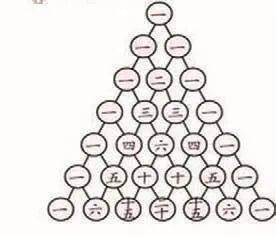
杨辉三角形，又称贾宪三角形，帕斯卡三角形，是二项式系数在三角形中的一种几何排列，我国南宋数学家杨辉所著的《详解九章算术》（1261年）一书中用如图的三角形解释二项和的乘方规律。

我们也可向同学们展示历史上曾经独立绘制过这种图表的数学家：贾宪（中国北宋11世纪《释锁算数》），杨辉（中国南宋 1261《详解九章算法》记载之功），朱世杰（中国元代1299《四元玉鉴》级数求和公式），阿尔·卡西（阿拉伯1427《算数的钥匙》），阿皮亚纳斯（德国1527），米歇尔·斯蒂菲尔（德国1544《综合算数》二项式展开式系数），薛贝尔（法国1545），B·帕斯卡（法国1654《论算数三角形》）。

这一个个历史人物，让我们带领这学生感受中国古代数学家的智慧，领略中国古代数学史曾经光辉灿烂的篇章。学生在课堂上不仅仅是了解杨辉三角在二项式定理中的用途，更能感受到杨辉三角曾经的历史，从而让学生对于杨辉三角有着深刻的印象，对于杨辉三角的学习也产生浓厚的兴趣。

了解历史，了解数学史，了解我国的数学史，学生学习到的不仅仅是书本中的知识，更是对历史的铭记，对于五千年文明的探求。

三、三角函数

三角函数是中职数学的重点也是难点所在，在学习三角函数的课堂中，学生对于满黑板的三角函数公式仿佛是到了英语课的课堂当中，那么三角函数为什么有此表示，是我们可以带领学生领略数学在世界的传播的魅力。

早期对于三角函数的研究可以追溯到古代，古希腊三角术的奠基人是公元前2世纪的喜帕恰斯，他按照古巴比伦人的做法，将圆周分为360等份，对于给定的弧度，他给出了对应的弦的长度数值，这个记法和现代的正弦函数是等价的，喜帕恰斯实际上给出了最早的三角函数数值表。当古希腊文化传播到古印度后，古印度人对三角术进行了进一步的研究。公元5世纪末的数学家阿耶波多提出用弧对应的弦长的一半来对应半弧的正弦。阿拉伯人也采用了古印度人的正弦定义，但他们的三角学是直接继承于古希腊，阿拉伯天文学家引入正切和余切、正割和余割的概念，并计算了间隔10分的正弦和正切数值表。进入15世纪后，阿拉伯数学文化开始传入欧洲，在翻译阿拉伯数学著作的同时，欧洲数学家开始制作更详细精确的三角函数表。16世纪后，数学家开始讲古希腊有关球面三角的结果和定理转化为平面三角定理。18世纪开始，随着解析几何分析学工具的引进，数学家们开始对三角函数进行分析学上的研究。欧拉的《无穷小量分析引论》对建立三角函数的分析处理做了最主要的贡献，使用接近现代的简写 sin、cos、tang、cot、sec和 cosec。而三角学传入中国开始于明崇祯4年（1631年），邓玉函、汤若望和徐光启合编《大测》中，首先将sine译为“正半弦”，简称“正弦”。

从中我们可以感受到数学在历史中一点点的积累与传播，每个国家的数学家都为数学史添上了辉煌的一笔。

数学的课堂，不仅是学习数学，更是了解数学的课堂，我们可以通过了解数学的历史，让学生感受到数学的魅力，看到数学的作用，从而更好的去学习数学。