扶正器对超深气井油管柱屈曲行为的影响研究*

牟易升，练章华，张　强，路宗羽，李　杰

(1.西南石油大学 油气藏地质及开发工程国家重点实验室，四川 成都 610500；2.中石油新疆油田公司 工程技术研究院，新疆 克拉玛依 834000)

0　引言

油管柱的屈曲行为会造成井下管柱路径的偏移，增大管体内部的应力，是很多油管损坏失效的诱因。屈曲行为到达一定程度后油管柱的纵向振动或扭转振动会加剧油管柱的磨损[1]。克深区块拥有非常严酷的“三超”气井，超深(6 000～8 000 m)、超高压(115～125 MPa)、超高温(170℃)，因此，油管柱处于极其恶劣的工作环境中，如果发生严重的屈曲行为，将极易损坏失效。扶正器作为一项能够改善油管柱屈曲行为的工具，能够有效减小油管的横向位移，是改善油管偏磨，保护油管柱完整性的有效措施[2]。

对于管柱的屈曲问题，国内外学者开展了大量的研究。1950年，Lubinski[3]开始对油管柱的屈曲行为研究，并提出正弦屈曲的概念；Paslay等[4]推导了井下管柱的正弦屈曲的临界载荷计算公式；Mitchell等[5-7]以Lubinski的理论为基础推导出屈曲的临界载荷计算公式；He 和 Kyllingstad[8]将Dawson推导的正弦屈曲临界载荷公式推广到弯曲井眼；Mitchell[9]推导了屈曲后的油管柱与套管的接触压力计算公式，并推导出套管屈曲后对油套管接触压力影响的载荷公式。对于扶正器的问题，国内外学者也有大量研究。Dareing等人[10]采用矩阵传递的方法建立了油管柱空间梁单元模型，求解出了油管单元各个位置的转角和弯矩；Juvkam-world等[11]建立了相邻扶正器间抽油杆柱最大径向变形量的计算模型，并提出杆柱最大挠度应小于杆管间隙为条件进行扶正器间距设计；张玉晓[12]建立了抽油杆扶正器配置间距的计算模型和抽油杆扶正器配置间距的计算模型；邓子麟等[13]根据势能驻值原理推导出了直井油管柱上相邻扶正器的临界失稳方程，通过该方程可得到扶正器间距的解析解。

以上的研究获得了一些理论公式和认识，对带有扶正器油管柱屈曲问题分析而言是重要的理论依据。然而对于自身处于复杂的力学工况中的油管柱，其中和点—封隔器段可能出现复杂的屈曲形态，前人的研究无法定量和完整的描述这复杂的屈曲形态。针对该问题，本文提出使用接触有限元法研究带扶正器的超深气井油管柱屈曲行为，为预防油管柱的屈曲行为和扶正器间距设计等问题提供理论参考。

1　油管柱失稳理论基础

油管柱在采油气作业中中和点往下的管柱可能处于受拉状态，也可能处于受压缩状态。油管柱的底部轴向力超过某一临界屈曲载荷时，管柱才会发生屈曲变形，其变形可能为正弦屈曲或螺旋屈曲，其横向变形可能会与井筒接触，产生接触压力。为了获得油管柱底部处的轴向力的大小和方向，根据带封隔器的油管柱的几种效应理论：活塞效应ΔL1、鼓胀效应ΔL2、摩阻效应ΔL3、温度效应ΔL4、螺旋屈曲效应ΔL5及永久性螺旋弯曲效应ΔL6等，从理论上可以计算出每种效应使油管柱产生的轴向形变，所有轴向形变相加，即可得到整个油管轴的综合变形量，见公式(1)。

ΔL=ΔL1+ΔL2+ΔL3+ΔL4+ΔL5+ΔL6

(1)

式(1)中，若ΔL>0，表示油管柱伸长，其伸长被封隔器和井口限制，因此封隔器处的油管柱受轴向压力作用；反之，若ΔL<0，表示油管柱缩短，整个管柱处于绷直状态。式(1)中的各种效应的计算公式见参考文献[14-15]。根据式(1)可以精确计算出油管轴底部的轴向力。

以塔里木油田某超深气井为例，表1为该井油管柱结构尺寸，管材钢级均为13Cr110，封隔器坐封在直径为196.85 mm的生产套管内。投产前的井口温度为16 ℃，地层温度为173 ℃，坐封后油管环空流体密度1.3 g/cm3，生产时井口压力介于83-92 MPa，无背压。

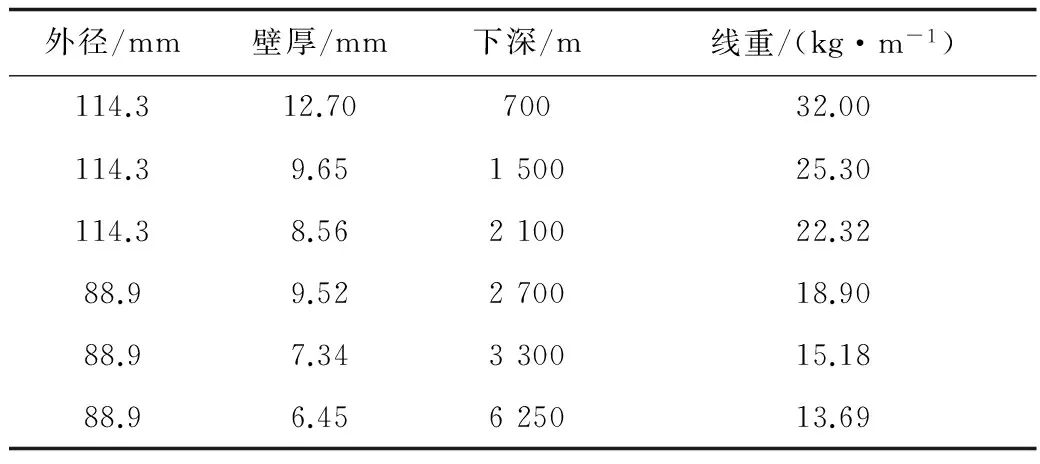
表1　油管柱参数Table 1　Parameter table of tubing

根据式(1)理论基础，应用本项目组开发的油管柱力学分析软件计算出当井口油压为83 MPa时，当产量为80×104m3/d，底部轴向力为191.4 kN，见图1所示。

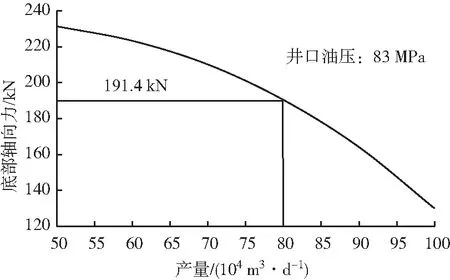
图1　底部轴向力随产量变化关系Fig.1　The diagram of the axial force on the yield variation

2　扶正器对油管柱屈曲影响分析

2.1　有限元模型建立

根据表1中油管柱结构尺寸，建立的油管柱有限元力学模型如图2所示。图2(a)中AB段为整个油管柱，不同的灰色度为不同尺寸的油管，A点和B点全约束。投产前后的温度变化如图2(b)所示。

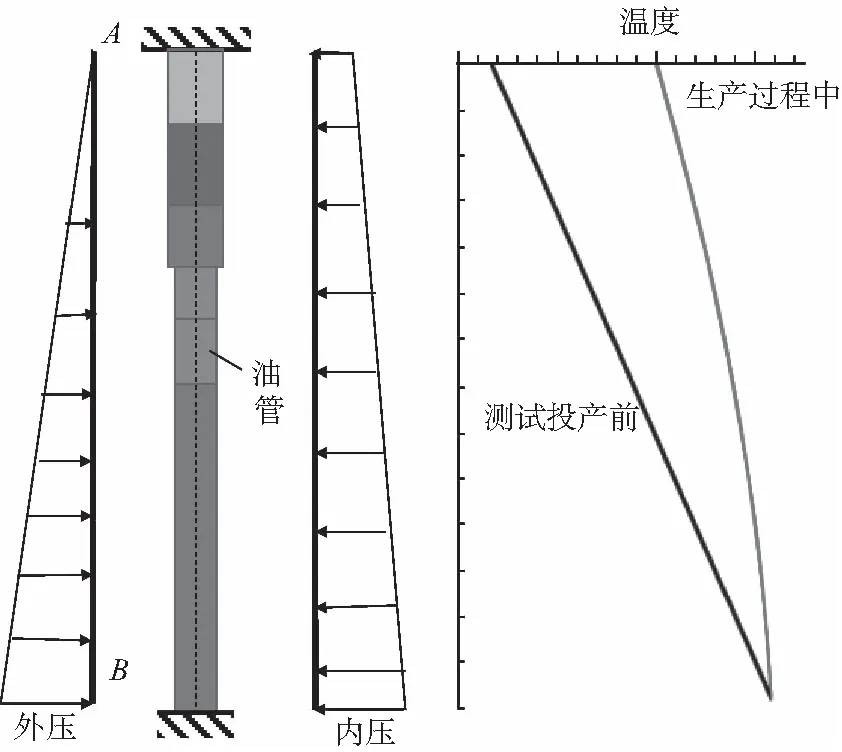
(a)压力　　　　　　　 (b)温度图2　油管柱压力温度条件示意Fig.2　Pressure and temperature environment of tubing

为分析扶正器对油管柱屈曲的影响，本文建立了原始油管和加扶正器油管的有限元力学模型，如图3所示。2个模型中的油管柱尺寸均参照表1的尺寸建立，同时均处于图2(b)所示的温度压力工况中。

建立的原始油管柱有限元力学模型见图3(a)。图3(a)中AB段为整个油管柱，不同的颜色为不同尺寸的油管，A点和B点全都固定约束，油管柱处于196.85 mm×12.7 mm生产套管的井筒中。油管柱边界条件有：内外流体压力、A点处的提拉力Fwh、管柱自重W、B点处的底部轴向压力Fb、温度变化引起的热应力。

加扶正器的油管柱有限元力学模型如图3(b)所示。图3(b)中，A′B′段为整个油管柱，不同的灰色度表示不同尺寸的油管，A′点和B′点全固定约束，油管柱处于196.85 mm×12.7 mm生产套管的井筒中，依据表1的油管柱结构计算出油管柱中和点高度为1 488.34 m，根据中和点的位置共安放8个扶正器，中和点以上扶正器2个，中和点以下扶正器6个，间距为100 m。加扶正器的油管柱边界条件有：内外流体压力、A′点处的提拉力Fwh′、管柱自重W′、B′点处的底部轴向压力Fb′、温度变化引起的热应力，扶正器的作用力。

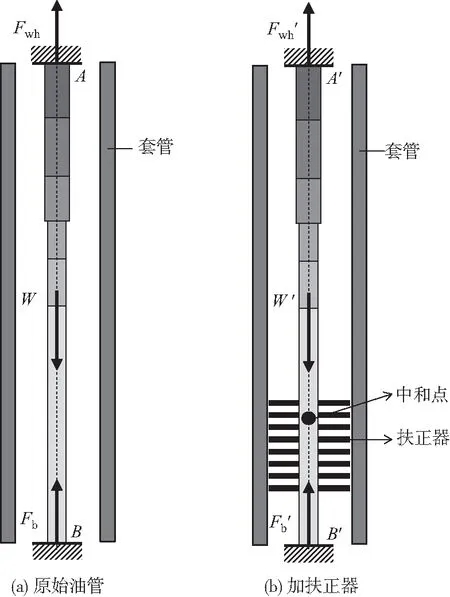
图3　油管柱有限元力学模型Fig.3　Finite element model of tubing

油管柱有限元模型选择ANSYS软件中PIPE288单元，该单元能够模拟油管柱内外流体密度产生的效应；同时，套管内壁与油管外壁之间的接触问题采用ANSYS软件中的线-线接触单元，以此研究油管柱与套管内壁的接触问题。扶正器有限元模型简化为套在油管柱外部的圆环状模型，也是PIPE288单元，长度为150 mm，外径为169.45 mm(套管内径为171.45 mm)，扶正器的有限元模型如图4所示。

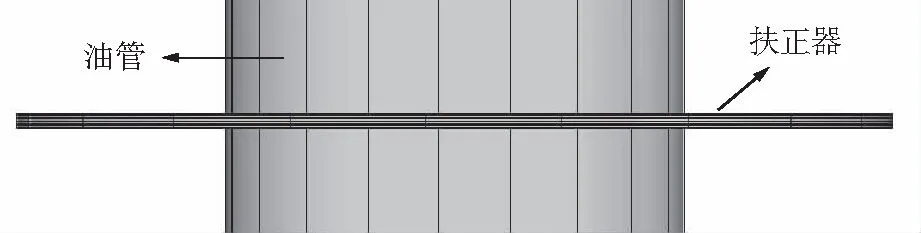
图4　扶正器有限元模型Fig.4　Finite element model of centralizer

2.2　油管柱屈曲形态与其横向位移分析

油管柱的屈曲问题属于非线性的力学分析过程，只有当底部轴向载荷越过一临界值时，油管柱才会发生屈曲变形。在油管柱生产过程中，为了保证油管柱的安全生产，需要尽量消除油管柱的屈曲形态，即寻求降低或消除油管柱底部的轴向压力，使其低于其临界屈曲失稳载荷。

由图3(a)所示的模型计算出原始油管柱在屈曲前后的轴向力沿井深分布如图5(a)和图5(b)所示，油管屈曲后井口油管提拉力下降了56 kN，中和点高度下降了90.67 m，底部轴向力由191.4 kN下降到127.29 kN。分析可知，油管可能已经与井筒接触产生了接触摩擦力，这些接触摩擦力抵消了一部分封隔器承受的底部载荷，从而引起了底部轴向力的下降。

由图3(b)所示的模型计算出加扶正器油管柱在屈曲后的轴向力沿井深分布，如图5(c)所示。比较图5(b)和图5(c)可知，加扶正器的油管柱井口油管提拉力下降了43 kN，油管屈曲后中和点高度下降了9.27 m，底部轴向力由127.29 kN增加到159.6 kN。分析可知，加扶正器的油管柱屈曲后与井筒的接触位置减少，可能只有扶正器与井筒接触，使得接触摩擦力变小，抵消封隔器的底部载荷少；因此，加扶正器油管柱的底部轴向力比原始油管屈曲后的底部轴向力大。

(a)屈曲前 　　　(b)屈曲后　　　(c)加扶正器　　图5　不同工况下油管柱轴向力分布Fig.5　Distribution of tubing axial force under different conditions

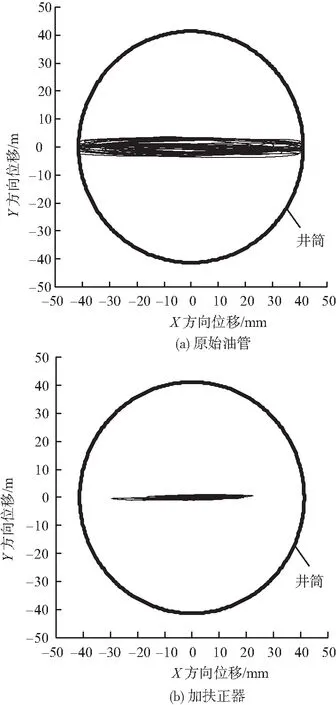
图6　不同工况油管柱横向位移俯视投影Fig.6　Horizontal displacement of tubingunder different working conditions

通过模拟得到2种工况下油管柱横向位移俯视图，见图6所示。由图6(a)可知，原始油管柱在图2(b)所示的温度压力条件下发生了非均匀的正弦屈曲，在X方向上油管柱已经与井筒接触。由图6(b)可知，在相同的温度压力条件下，加扶正器的油管柱同样发生了正弦屈曲，但是X，Y方向上横向位移均明显小于原始油管，并且X方向上油管柱未与井壁接触。比较图6(a)与图6(b)可知，2种工况下油管均发生正弦屈曲，但安放扶正器后油管柱的屈曲形态得以改善，X和Y方向的横向位移均明显减小，并且避免了油管与井筒接触。

图7为2种工况下油管横向位移随井深变化关系图，原始油管已经发生了非均匀的正弦屈曲，在X方向上已与井筒接触，Y方向上也有一定量的位移，原始油管从上而下开始发生屈曲的位置在井深5 868.57 m处，共有381.43 m的油管段发生了屈曲，见图7(a)所示。加扶正器油管柱也发生了正弦屈曲，但X，Y方向的横向位移均小于原始油管，油管在X方向也未与井筒接触，加扶正器油管从上而下开始发生屈曲的位置在井深5 576.23 m处，共有673.77 m的油管段发生了屈曲，比原始油管的屈曲段长292.34 m，如图7(b)所示。

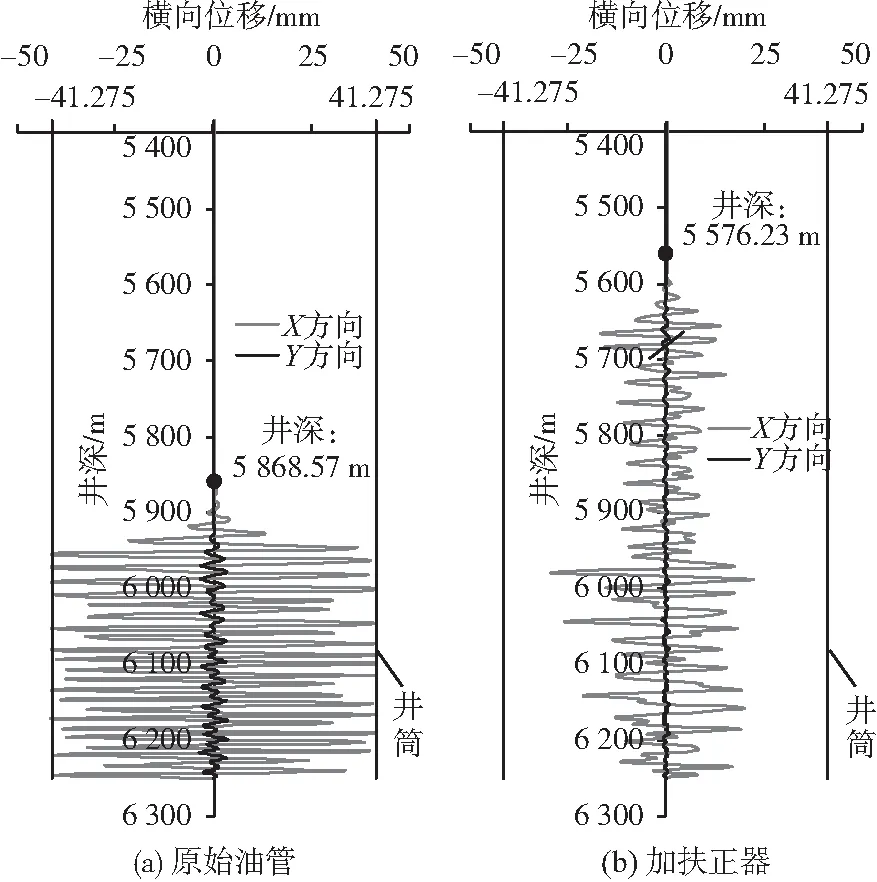
图7　不同工况油管柱横向位移随井深变化关系Fig.7　The horizontal displacement of tubing bythe well deep variation in different working conditions

分析可知，当底部轴向力超过一定临界值后，油管会发生屈曲变形，从能量角度而言，由于底部轴向力对油管的做功，油管以屈曲的形式存储弯曲应变能，弯曲应变能与屈曲段长度和横向位移成正比，由于扶正器的作用力使得油管横向位移减小，油管以增长屈曲段的形式来平衡弯曲应变能，因此加扶正器的油管横向位移小，而屈曲段变长。

图8为2种工况下油管屈曲形态的轴向投影图，由图8可知，原始油管X方向最大位移为41.275 mm，与井壁接触，Y方向最大位移为3.663 mm；安放扶正器后油管X方向最大位移为29.349 mm，Y方向最大位移为1.035 mm，分析可知，安放扶正器油管屈曲状态得到了改善，油管与井壁未接触。

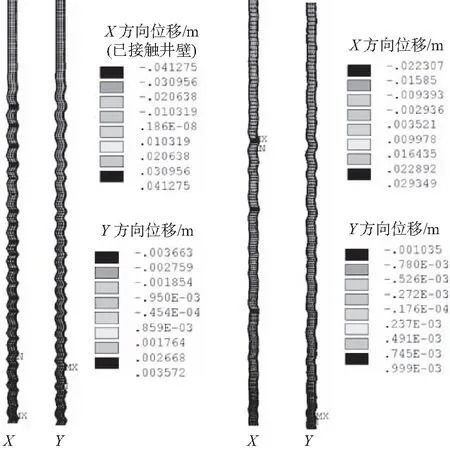
(a)原始油管　　　　　　(b)加扶正器图8　不同工况油管屈曲形态的轴向投影Fig.8　The axial projection of the buckling form of tubing in different working conditions

2.3　油管-套管接触压力分析

在实际工况中，油管柱与套管接触后会发生磨损，由图6可知，原始油管已经与井筒接触，加扶正器油管未与井筒接触，因此接触压力始终为0。图9为原始油管柱屈曲变形后与生产套管内壁的接触位置及其接触压力随井深分布关系图。

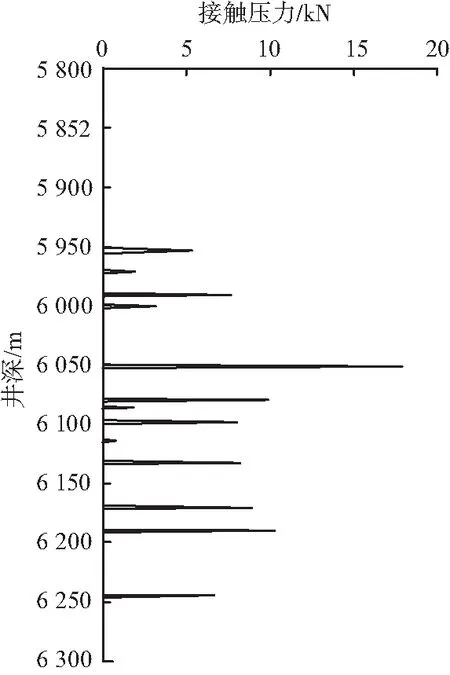
图9　原始油管柱接触压力分布Fig.9　Contact pressure distribution of tubing

从图9中可知这原始油管柱屈曲后与井壁接触位置发生在井深5 952.28～6 244.77 m，即292.49 m的范围内与井壁有接触。而从图7中可知原始油管的屈曲段的范围为381.43 m，即油管柱屈曲接触段顶部还有88.94 m的屈曲段未与井壁接触。图9中给出了其接触压力的定量数据，该数据乘以油管柱与套管内壁的摩擦系数即可得其油管柱与套管内壁的摩擦力，根据这些数据可以进一步地分析油套管柱之间的磨损量及其开展磨损失效分析，为油套管损伤失效分析提供理论数据和依据。

从图9中接触压力的分布大小可知，接触压力较大值主要分布在接触部位的中部，最大接触压力为18 kN，位置在井深6 051.69 m处，接触部位中，顶部与底部的接触压力较小，分布也较分散。

3　结论与认识

1)建立了超深气井原始油管柱和带扶正器油管柱屈曲、接触问题分析的有限元模型，该模型可以对全井段原始油管柱及带扶正器油管柱屈曲形态进行分析，可以得到管柱定量的屈曲形态和原始油管屈曲后与套管的接触压力及其摩擦力，可为扶正器位置设计和油套管摩擦损伤失效分析提供定量的数据参考。

2)超深气井中，原始油管与加扶正器油管均在中和点到封隔器段发生了非均匀的正弦屈曲，但原始油管横向位移大并且与井筒接触，而加扶正器油管横向位移小，屈曲段长。

3)加扶正器能有效减少油管柱横向位移，改善油管屈曲形态，有利于在预防油管磨损的同时提高管柱的使用寿命。

[1] 杨海滨, 狄勤丰, 王文昌. 抽油杆柱与油管偏磨机理及偏磨点位置预测[J]. 石油学报, 2005, 26(2):100-103.

YANG Haibin, DI Qinfeng, WANG Wenchang. Prediction of serious abrasion position and mechanism of uneven abrasion between sucker rod string and tubing[J]. ACTA PETROLEI SINICA，2005，26(2):100-103.

[2] 朱君. 有杆抽油系统井下工况诊断方法研究[D].绥化： 大庆石油学院，2004.

[3] LUBINSKI A. A Study of the Buckling of Rotary Drilling Strings[J]. Drilling & Production Practice, 1950.

[4] SCHWIND B E, WOOLEY G R. New Findings on Leak Resistance of API 8Round Connectors[J]. SPE Production Engineering，1989, 4(4)：466-472.

[5] MITCHELL R F. Comprehensive Analysis of Buckling With Friction[J]. Spe Drilling & Completion, 1996, 11(3):178-184.

[6] 刘凤梧, 高德利. 封隔器对油管螺旋屈曲的影响分析[J]. 清华大学学报(自然科学版), 1999, 39(8):104-107.

LIU Fengwu, GAO Deli. Packer effect analysis of helical buckling of well tubing[J]. Journal of Tsinghua University (Science and Technology)， 1999, 39(8):104-107.

[7] MISKA S, QIU W, VOLK L, et al. An Improved Analysis of Axial Force Along Coiled Tubing in Inclined/Horizontal Wellbores[J]. Directional Drilling，1996:207-214.

[8] HE X，KYLLINGSTAD A. Helical Buckling and Lock-Up Conditions for Coiled Tubing in Curved Wells[J]. Spe Drilling & Completion, 1995, 10(1):10-15.

[9] MITCHELL R F. Buckling of tubing inside casing[J].SPE Drilling & Completion, 2012, 27(4): 486-492.

[10] DAREING D W, AHLERS C A. Tubular bending and pull-out forces in high-curvature well bores[J]. Journal of Energy Resources Technology, 1991, 113:2(2):133-139.

[11] JUVKAM-Wold H C, WU J. Casing Deflection and Centralizer Spacing Calculations[J]. Spe Drilling Engineering, 1992, 7(4):268-274.

[12] 张玉晓.杆管偏磨治理理论与技术[D].东营:中国石油大学(华东)，2009: 59-68.

[13] 邓子麟，练章华，张强，等. 直井油管柱扶正器间距设计研究[J]. 中国安全生产科学技术, 2016, 12(9):60-64.

DENC Zilin, LIAN Zhanghua, ZHANG Qiang, et al. Study on spacing design of tubing string centralizer in vertical well[J].Journal of Safety Science and Technology, 2016, 12(9):60-64.

[14] 桑果. 川西地区油管管柱力学行为及优化设计研究[D].成都：西南石油大学，2016.

[15] 练章华，魏臣兴，宋周成，等. 高压高产气井屈曲管柱冲蚀损伤机理研究[J]. 石油钻采工艺, 2012, 34(1):6-9.

LIAN Zhanghua，WEI Chenxing，SONG Zhoucheng. Erosion damage mechanism of buckled tubing in high pressure and high production gas wells[J]. Oil Drilling & Production Technology, 2012, 34(1):6-9.