金属矿山采空区形状分形特征探索

胡建军

(1.北京科技大学土木与资源工程学院，北京 100083；2.北京矿冶科技集团有限公司，北京 100160)

金属矿床是经过一系列长期复杂的地质运动与作用而形成的，其空间分布特点表现为杂乱而无序，品位分布也呈现不确定性[1-2]。矿山开采根据矿体赋存情况而进行设计，开采后遗留采空区与矿体分布有相似的空间形态，加之开采过程中受到构造、地应力、爆破震动等多重作用，其形态表现更为不确定性及非线性。三维激光扫描技术在采空区探测中的应用[3-5]，使得采空区形态的可视化和精确测量得以实现，从而利用非线性手段研究采空区形态也变为可能，用非线性的理论方法深入研究釆空区空间特征及边界特性，也必然是未来发展的趋势[6-8]。

分形理论由B.B.Mandelbrot等第一次提出[9]，之后得到了快速发展，其数学基础是分形几何学，即由分形几何衍生出分形信息、分形设计、分形艺术等应用。在岩体地质、孔洞等方面，分形理论被广泛应用于对岩溶管道(洞穴)形态的数学描述、分形计算以及机理特征研究[10-12]，有学者将分形理论运用于对铁路的岩溶洞穴预报[13]，但对于矿山采空区形态分形特征研究方面较为少见，不同于岩溶等地下孔洞的三维形状分形特点，矿山采空区为人为扰动形成，受矿体特征、爆破震动、采掘计划等影响较大，其不规则程度主要表现在其边界曲面上。De wijs[14]首次利用分形理论研究了矿体品位分布，并证明了矿体品位的空间分布具有分形特征，矿山开采过程对于矿床来说属于局部作用过程，即矿山开采形成的采空区，其分布及形态与矿体品位的空间分布应具有一定相关性。

1　计盒维数

在众多计算分形维数方法中，计盒维数概念比较清晰，计算相对简单明了，从而得到了广泛的应用[15-16]。该方法用边长或半径为r的正方形网格、立方体、圆形或球体对研究对象逐次进行栅格化处理，得到一系列不同网格边长r对应的非空格子数量N(r)，绘制N(r)与r的双对数散点图并进行拟合，若其具有明显的线性特征，即无标度特性，说明具有分形特征。由分形定义可知[17]：N(r)=Ar-D，两边取对数变换，得：lnN(r)=lnA-Dlnr，线性拟合的直线斜率绝对值即为分维值。

2　单采空区分形特性

为了揭示研究方法的适用性以及采空区分形特征的普遍性，本研究选取不同矿山的四个采空区进行平行对比研究，以求发现采空区分形的共性特征和普遍性特点。为描述问题方便，四个采空区分别用简写代号SZY、LM、JM、WF代替，各采空区均借助BLSS-PE矿用三维激光扫描系统[18]进行精确探测，获得采空区实体图，并对实体模型进行切剖面处理，每个采空区选择4个具有代表性的剖面，如图1所示。

对于一维边界线及二维平面，首先采用边长为r的正方形网格进行覆盖，随后以1/2倍的比例逐次缩小网格尺寸，得到一系列对应的r和Nn(r)，绘制lnNn(r)～lnr散点图，并进行线性拟合得出线段的斜率，其绝对值即为盒维数D。而对于三维空区边界曲面及三维空间体，则可采用边长为r的三维立方体进行覆盖，使用上述方法计算其盒维数D。

2.1　一维边界线分形特性

以剖面SZY-4边界线为例，根据盒维数计算原理，首先选择r=10 m的正方形网格进行覆盖，可得此时N1(10)=12；然后r=5 m，得N2(5)=21；同理可得N3(2.5)=43，N4(1.25)=89，对应的网格覆盖图如图2所示，图2中阴影部分为有效盒子数。

以lnr为横坐标，lnNn(r)为纵坐标绘制散点图，对应的关系曲线如图3所示，拟合直线的斜率的同理求得四个采空区各剖面边界线的相关系数及计盒维数如表1所示。对比分维值计算情况，各剖面边界线lnNn(r)～lnr曲线线性拟合相关系数R2=0.992～1.000，均高度线性相关，即存在分形特征；另外，可以看出边界起伏程度较大的边界线，其盒维数值也较大，非线性程度也大。从而，计盒维数可作为采空区边界线复杂程度的定量指标。

图1　各采空区实体图及剖面位置

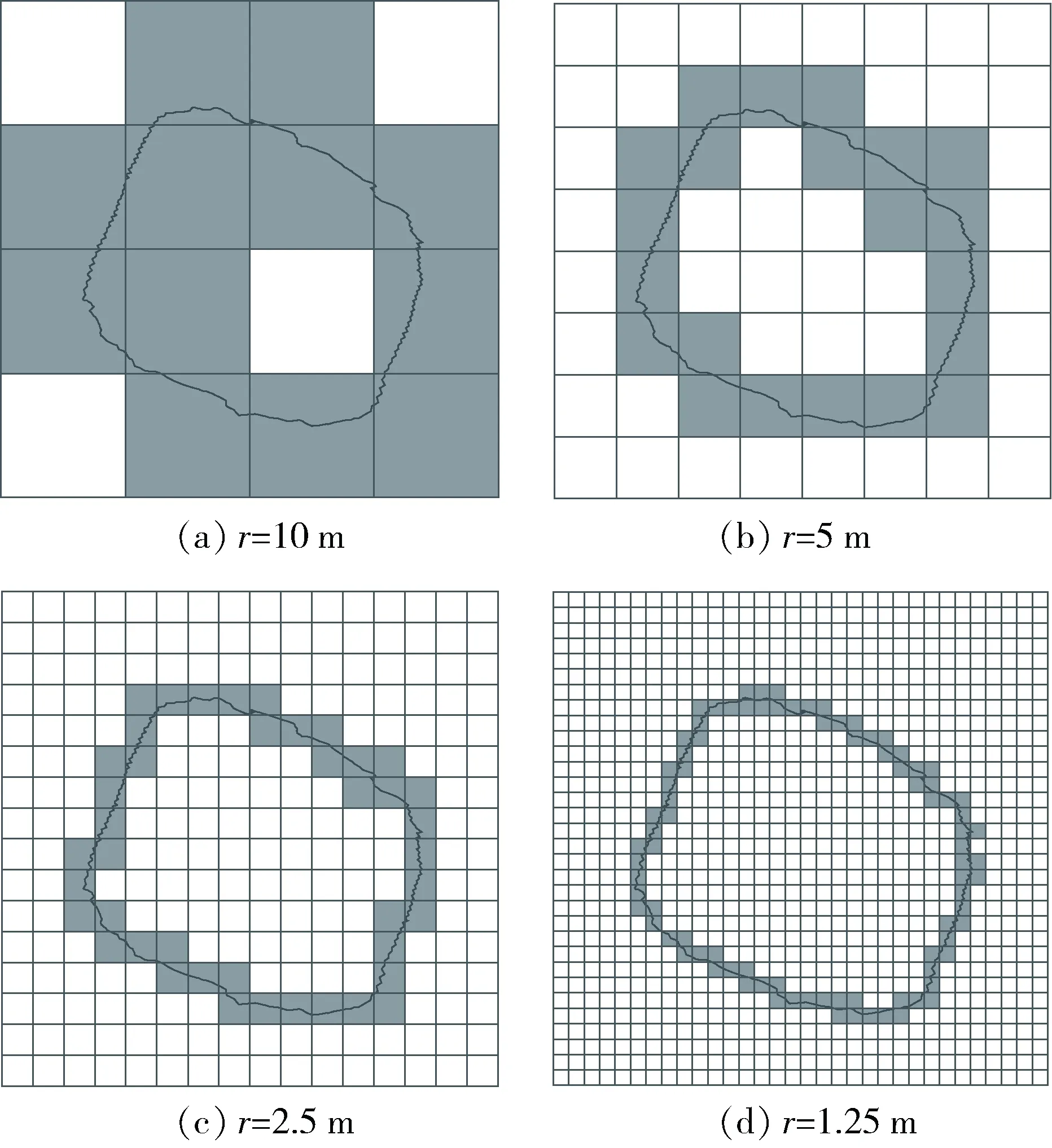
图2　剖面SZY-4边界线网格覆盖计算图

绝对值0.9404即为盒维数值D，同时可求得线性相关系数R2=0.9978。

图3　剖面SZY-4边界线lnNn(r)～lnr关系曲线

表1　各采空区剖面边界线分维值

剖面名称SYZ-1SYZ-2SYZ-3SYZ-4LM-1LM-2LM-3LM-4JM-1JM-2JM-3JM-4WF-1WF-2WF-3WF-4网格数/个r=10m19201044448755891194r=5m363521669918141212141926196r=2.5m101864512131717343326203436524112r=1.25m24516794222839387071575175781218222相关系数R20.9920.9931.0000.9980.9900.9820.9980.9980.9980.9990.9990.9890.9920.9990.9981.000计盒维数D1.2551.0481.0800.9400.8380.9541.0771.0661.0311.1261.1651.0791.0971.0271.1381.067

2.2　二维平面分形特性

一维边界线分维值可有效表达空区剖面边界的复杂程度，但其不能全面反映二维平面的复杂程度，本节拟在边界线分析的基础上，考虑剖面内部包含属性，利用计盒维数分析剖切平面区域的二维分形特性，仍然采用网格覆盖法进行分维值计算，在边界线网格覆盖的基础上，将边界内部包含网格也计算在内，得到新的网格数，重新计算计盒维数。

仍以SZY-4剖面为例，其网格覆盖图盒子数分别为N1(10)=13，N2(5)=32，N3(2.5)=104，N4(1.25)=353，对应的网格覆盖图见图4。

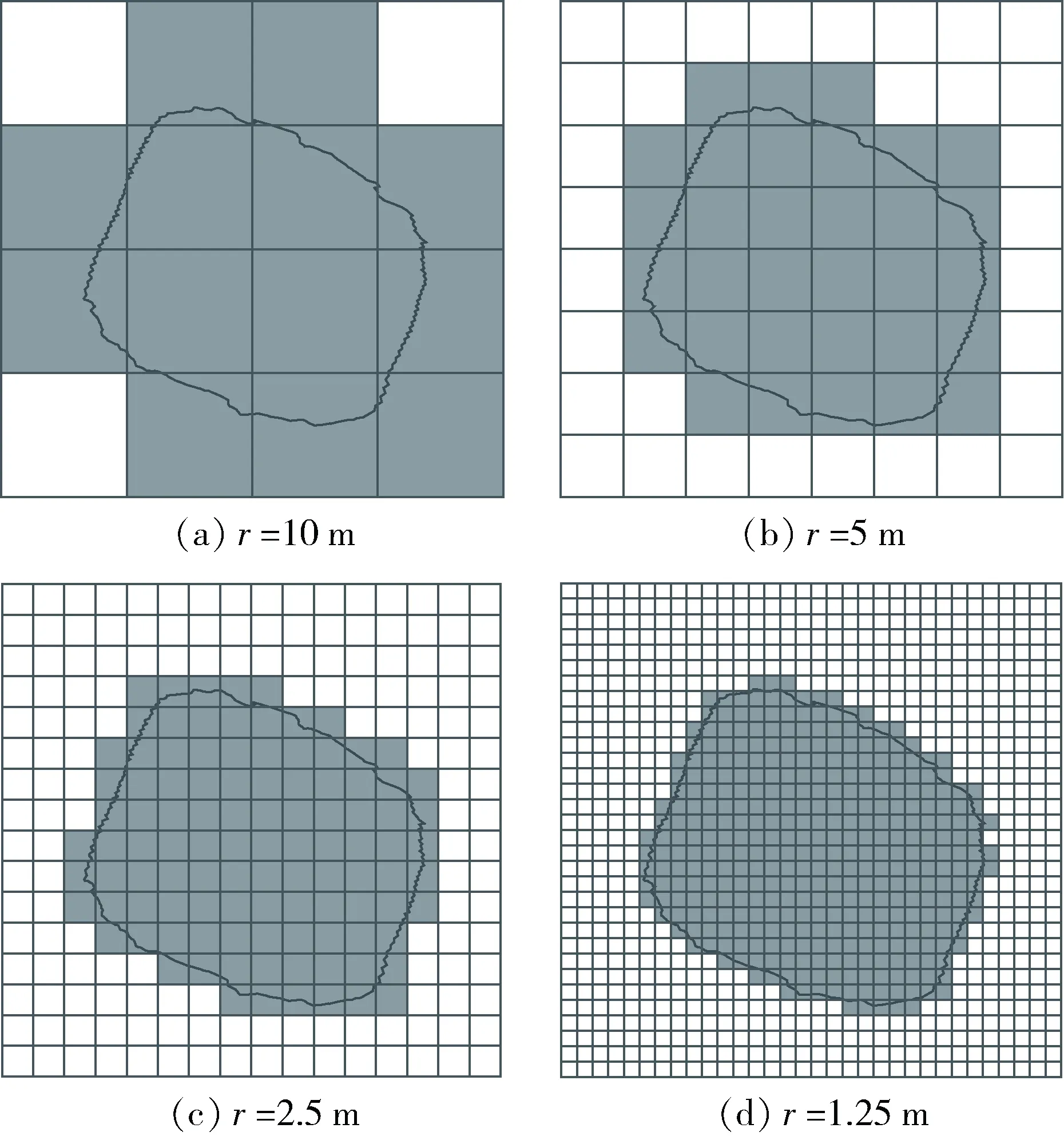
图4　剖面SZY-4区域网格覆盖计算图

2.3　采空区三维分形特性

常规矿山空场法开采，空区顶板及边界面是典型的非线性空间曲面，无法用常规的几何理论进行定量描述。前述研究表明，单个采空区任何一个剖面的边界线和平面区域都具有分形特性，本部分拟针对采空区三维边界曲面和三维空区体的分形特性开展研究，揭示其内在特点。

2.3.1三维边界面分形特性

四个采空区三维界面曲面的计盒维数计算结果见表3，可以看出线性拟合相关系数R2=0.999～1.000，其线性相关度均极强，即各空间边界曲面存在非常好的分形特征；另外，可以看出边界曲面的盒维数值均大于平面或边界线，其边界复杂程度更为综合、明显。

2.3.2空区体三维分形特性

三维边界曲面的分维值计算，很好的表达了采空区边界曲面的分形特性，但其未包含空区内部空间的属性。将三维边界曲面覆盖立方体与内部空间立方体数相加，重新计算得到空区体计盒维数。四个采空区整体的计盒维数计算情况如表4所示，线性拟合相关系数R2=0.994～0.998，表明其具有线性相关性，即各采空区空间体也存在很好的分形特征。

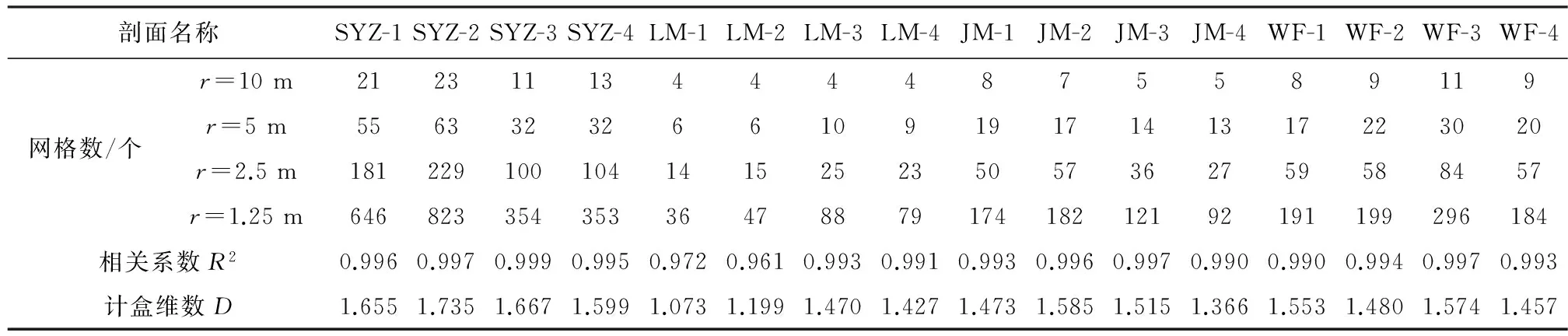
表2　各采空区剖面分维值

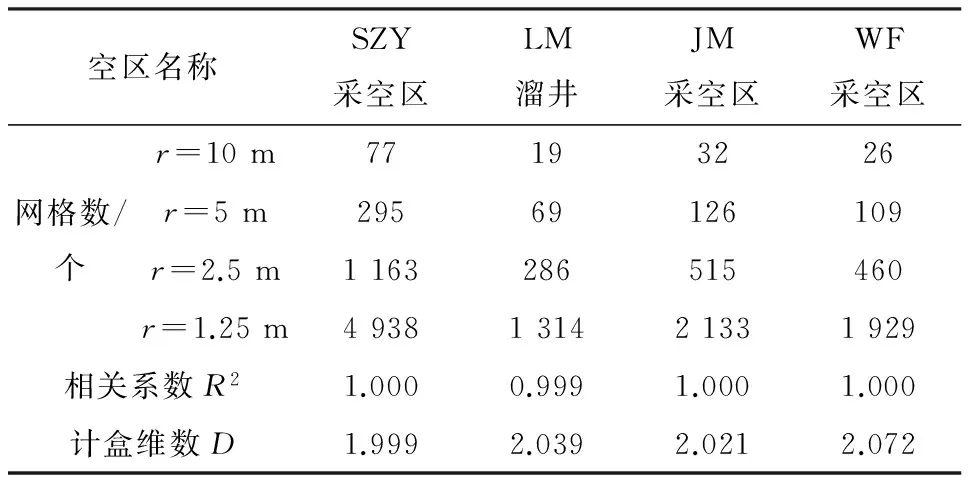
表3　各采空区三维边界面分维值

表4　各采空区三维体分维值

3　某钨矿采空区群顶板分形特征

前述各矿山单个采空区的一维边界线、二维平面区域、三维边界曲面、三维空区体都具有很好的分形特征，然而，采矿现实中，采空区大多以空区群形式存在，尤其全面法开采后留下的采空区，其矿柱视顶板情况、开采环境预留，大小不一，各空区相互贯通，形态十分复杂。采空区群的空间复杂赋存分布，各采空区共同作用下形成了复杂的顶板形态，研究顶板的形态可以表征采空区群的边界特征。本研究以某钨矿空区群为例，在三维激光精细扫描的基础上，将单采空区分维值计算方法拓展至采空区群顶板分维值计算，研究其顶板三维曲面的分形特征。

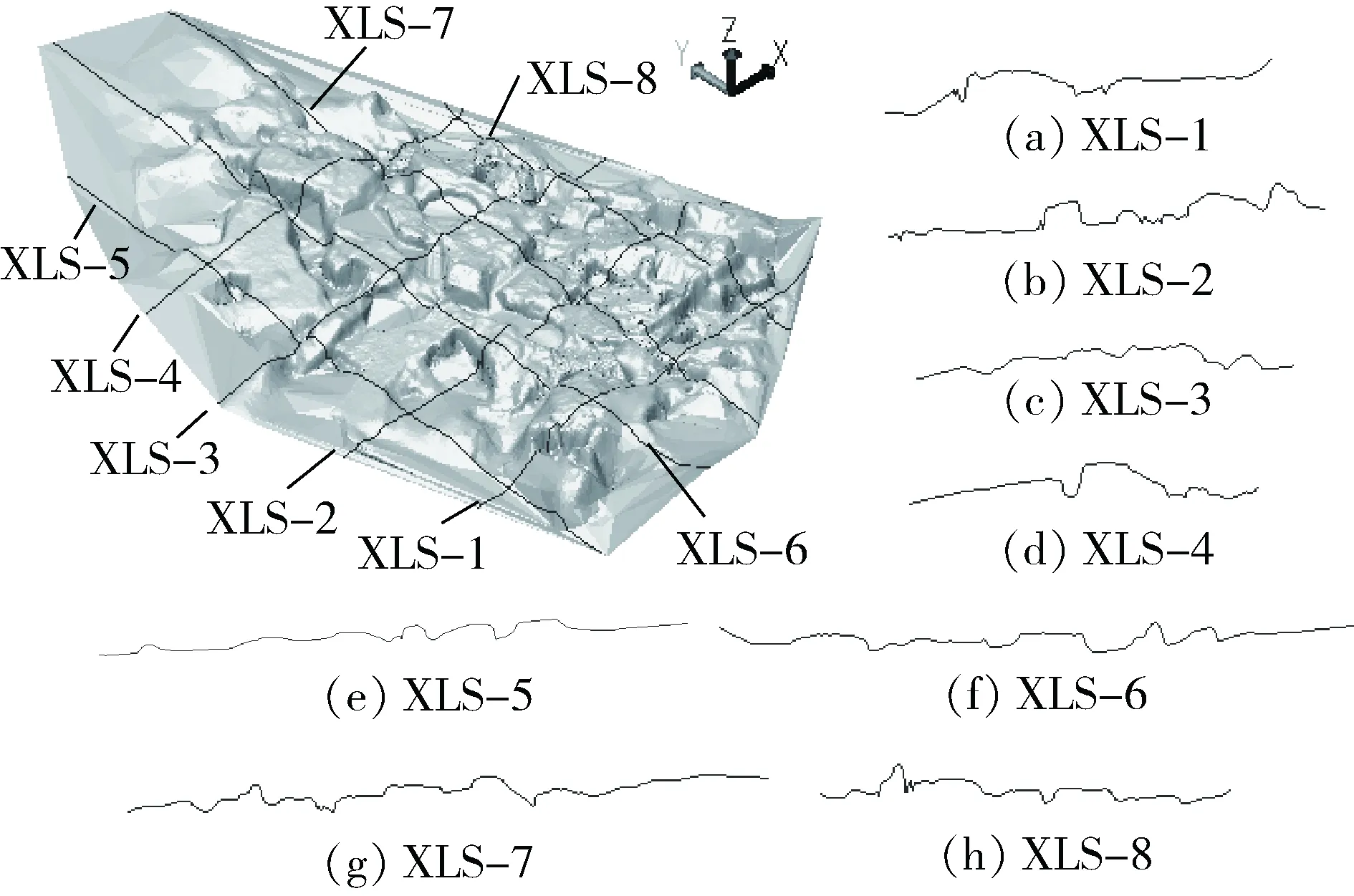
图5　某钨矿采空区群顶板所选剖面位置

表5　某钨矿采空区群顶板各剖面分维值

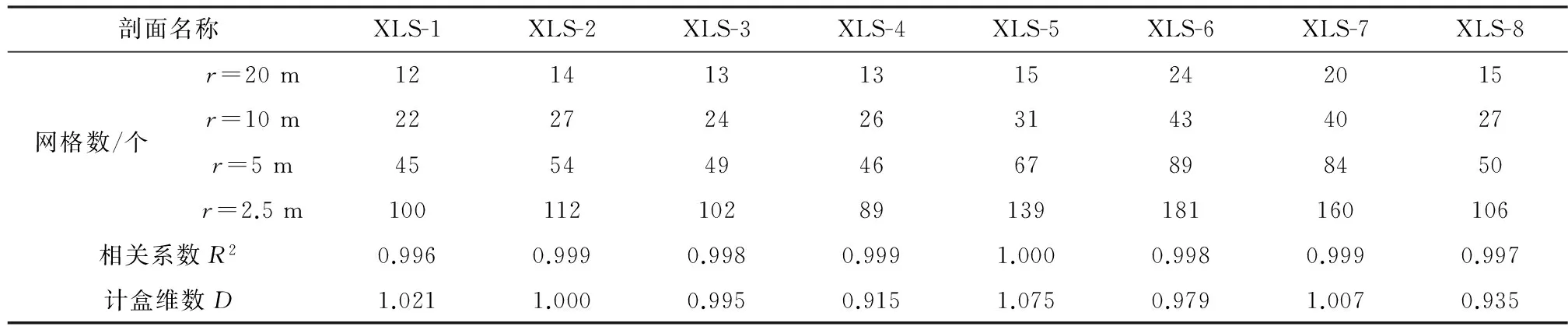
剖面名称XLS-1XLS-2XLS-3XLS-4XLS-5XLS-6XLS-7XLS-8网格数/个r=20m1214131315242015r=10m2227242631434027r=5m4554494667898450r=2.5m10011210289139181160106相关系数R20.9960.9990.9980.9991.0000.9980.9990.997计盒维数D1.0211.0000.9950.9151.0750.9791.0070.935

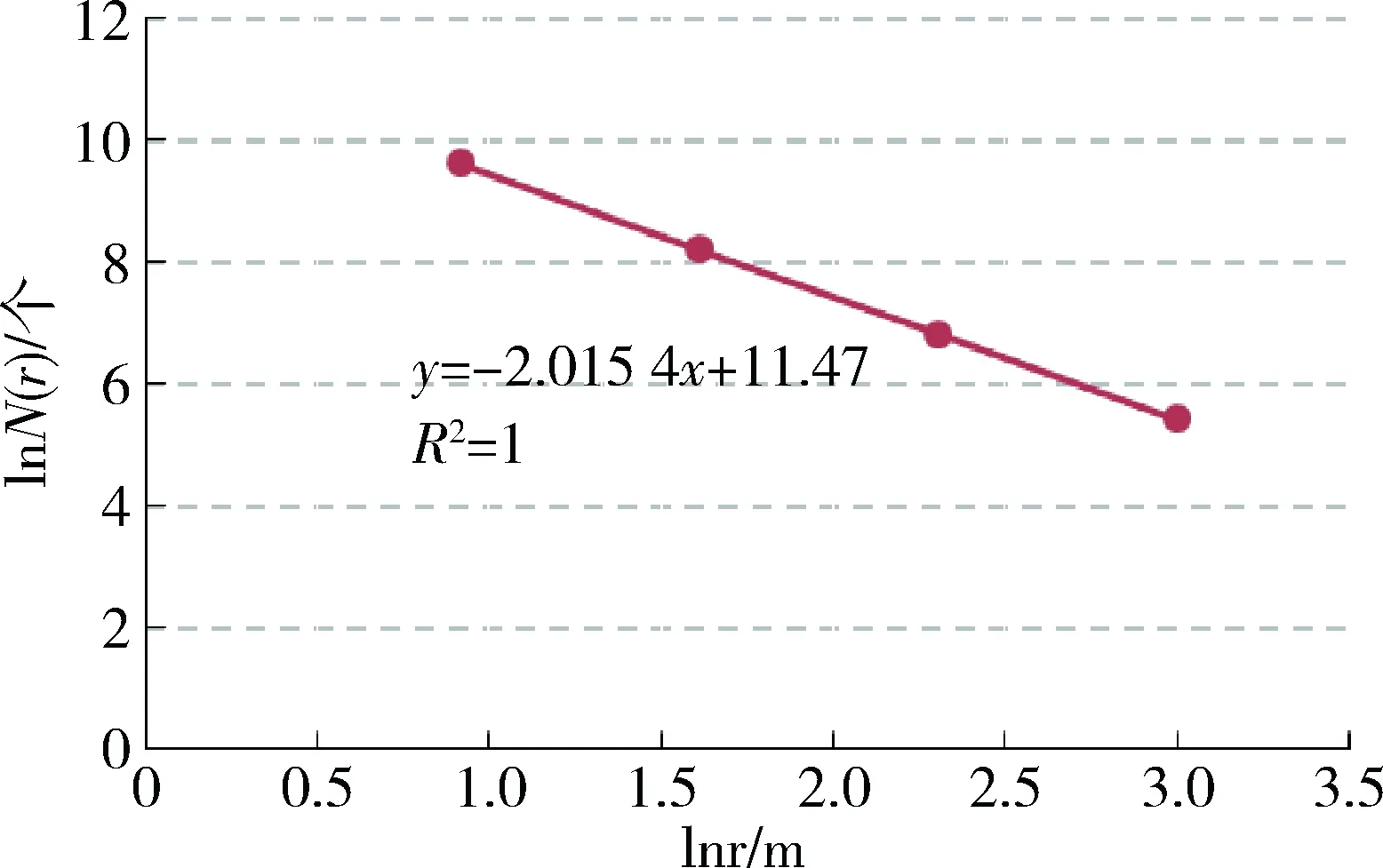
图6　采空区群顶板曲面lnNn(r)～lnr关系曲线

同样，为便于研究，将采空区顶板进行剖切面处理，图5为某钨矿采空区群顶板所选剖面位置，各剖面分维值计算情况见表5，可以看出各剖面具有明显的分形特征。

进一步计算整个采空区群顶板的三维曲面计盒维数，并绘制顶板曲面lnNn(r)～lnr曲线图如图6所示，可以看出线性拟合相关系数R2=1，表明其具有极强线性相关性，即采空区群顶板曲面存在很好的分形特征。

4　结　论

1) 通过四个不同矿山单采空区的一维、二维、三维空间分形特征研究可知，采空区形状在各维度上均具有良好的分形特性，自相似性程度很高，计盒维数的大小与其复杂程度有密切关系。将该方法拓展至采空区群分析，结果表明采空区群顶板三维曲面形状也具有明显的分形特征。

2) 分维值是反映采空区复杂程度的定量参数，其为复杂采空区研究提供了一种新的方法，在采空区形状预测、采空区围岩质量分级、稳定性评价等方面具有广阔的应用前景，但由于采空区本身的复杂性、随机性，所提出的采空区分形特征普遍性尚有待大量工程实践验证，并进一步拓展研究深度和广度。

[1]成秋明.成矿过程奇异性与矿床多重分形分布[J].矿物岩石

地球化学通报,2008,27(3):298-305.

[2]刘岳.区域地球化学数据分析及成矿信息融合模型研究--以南岭成矿带为例[D].北京：中国地质大学(北京),2015.

[3]战凯,陈凯,张达.三维激光扫描技术在采空区群探测中的应用[J].矿业研究与开发,2016,36(2):24-27.

[4]余乐文,张达,张元生,等.采空区三维激光扫描智能化监测技术研究与应用[J].有色金属:矿山部分,2015,67(3):1-3.

[5]任洪文,刘兆富,韩智尧,等.三维激光扫描技术在测绘采空区中的应用[J].黄金科学技术,2013,21(3):64-68.

[6]付建新.深部硬岩矿山采空区损伤演化机理及稳定性控制[D].北京：北京科技大学,2014.

[7]张绍国,王新民,姚建,等.采空区稳定性的非线性分析[J].地下空间与工程学报,2005(6):908-911.

[8]付建新,宋卫东.基于分形理论的复杂采空区空间特性定量研究[EB/OL].[2016-06-17].http:∥www.paper.edu.cn/releasepaper/content/201606-743.

[9]MANDELBROT B B,VAN Ness J W.Fractional Brownian motions:fractional noise and application [J].SIAM Review,1968,10(4):422-437.

[10]李文兴.岩溶洞穴的分形弯曲度[J].中国岩溶,1995,14(3):241-245.

[11]李文兴.岩溶管道介质空隙率(视表征体元)及分形研究[J].中国岩溶,1995,14(2):161-168.

[12]胡章喜,沈继方.岩溶形态系统的分形特征及其机理探讨[J].地球科学:中国地质大学学报,1994,19(1):103-108.

[13]蒋忠信,王衡.南昆铁路岩溶洞穴预报技术[J].水文地质工程地质,2002(2):69-73.

[14]DE Wijs H J.Statistics of ore distribution:(1) frequency distribution of assay values [J].Geol Mijnbouw,1951,13:365-375.

[15]崔建江,贾旭,刘晶,等.基于计盒维数和多小波的静脉图像特征提取[J].东北大学学报:自然科学版,2010,31(10):1397-1400.

[16]PEITGEN H O,JURGENS H,SAUPE D.Chaos and fractals[M].Berlin:Springer-Verlag,1992:202-213.

[18]杨斐文,张达,杨小聪,等.基于Cortex-M4和FreeRTOS的矿用三维激光扫描测量系统设计[J].中国矿业,2014,23(S2):316-318.