等边布置三方柱绕流漩涡相互作用机制的数值分析

刘 欢

（天津城建大学 能源与安全工程学院，天津 300384）

众所周知，在一定雷诺数条件下，黏性流体流经柱体时，在逆压梯度作用下，流体边界层发生分离，引发周期性的漩涡脱落.这种涡旋的产生和脱落现象给工程带来不利的影响，甚至发生工程事故.例如在1940年，美国华盛顿州建成刚4个月的塔科马海峡大桥，在未达其设计风速一半的气候条件下，因涡激振动而造成桥梁主体的共振，最终结构溃塌[1]；飞机与船只等，在流体中运动时，由于尾部所产生的涡旋消耗动能，形成航行时的阻力.这些都是不利于生产实践的.同时还应该注意到，有时流体的涡旋运动也具有积极的工程意义.例如，西班牙的初创公司研发了一套全新的风力涡轮发电机——Vortex Bladeless，这是一套没有叶片的涡轮机，它是靠周围空气的运动形成漩涡，然后带动设备前后晃动起来，再利用塔架底部的两个环形相斥磁铁作为非电动机马达，通过底部相斥的磁铁推动时椎体持续产生最大震荡，震荡时产生的机械能就会透过锥体底部的交流发电机，将力学能转换为电能.因此，研究柱体绕流涡旋生成、演化及脱落规律，不仅具有基础的理论意义，也具有重要的实际工程价值.

近年来，柱体的绕流已经从圆柱转向方柱，柱体个数及排列方式也多种多样.张伟等[2]采用有限体积法对雷诺数Re为100的等边布置三方柱的二维绕流问题进行了数值模拟.考虑左“品”字形和右“品”字形两种柱体几何布置，间距比在1.5～5.0变化、右“品”字形布置时，对流场特性与结构受间距比的影响较小，在所研究范围内，未出现偏流现象.在较小间距比时，右“品”布置的流动稳定性比左“品”字形布置更稳定.

Okajima[3]运用实验研究的方法，研究了Re在70～20 000时，不同截面纵横比的矩形截面柱体的斯特劳哈尔数St与雷诺数Re的关系，并详细分析了在不同的雷诺数下，矩形柱的长高比率不同时，方柱后尾迹的基本频率和能谱的变化.

赵心广[4]对高雷诺数下右“品”字等边布置的三方柱绕流进行了数值模拟，发现上游两个方柱的阻力系数比下游方柱小，上游两方柱升力系数比下游方柱大，并且下游方柱的升力系数在零附近振荡；郭明旻等[5]以三方柱模型实验结果为依据，讨论了建筑物表面风压脉动的极值分布情况，并发现在间距比2.5～3.0间流场可能存在突变；张爱社等[6]用有限元方法对雷诺数Re为200的等边布置的二维绕流问题进行数值模拟，研究表明三圆柱之间的干扰在小间距比情况下比较严重，流动偏向下游的某个圆柱.

笔者对Re为100和200的低雷诺数条件下，等边左“品”字形布置的三方柱二维绕流问题进行数值模拟研究.考虑到间距过小三方柱会出现重合，而间距过大三方柱间又不再有相互影响，所以取间距比为1.2～6.0.通过局部区间进行间距比的加密，对流场流线、涡量图以及阻力系数、升力系数、斯特劳哈尔数的分析，研究流场流动特性、柱体阻力系数、升力系数及斯特劳哈尔数的变化规律，特别关注了对流场流动和动力特性具有重要影响的临界间距比.

1 数值研究方法

1.1 控制方程和相关参数

采用有限体方法，求解二维黏性不可压非定常流场；压力采用二阶离散格式，动量采用二阶迎风格式，压力与速度耦合采用SIMPLE算法.

二维黏性不可压非定常流动的控制方程为连续性方程和不可压Navier-Stokes方程

方程中的下标采用了求和约定.vi、p、t分别为速度分量、压力和时间；ρ为流体密度；μ为流体动力黏性系数.

阻力系数、升力系数、间距比及St数等无量纲数的定义为

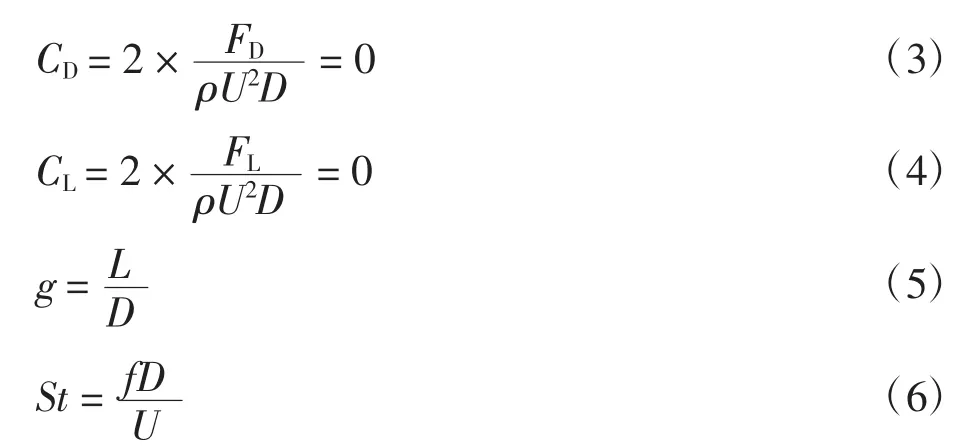
式中：CD为阻力系数，正方向与来流方向相反；CL为升力系数，正方向与来流方向垂直；FD为阻力；FL为升力；ρ为流体密度；U为来流速度；D为方柱边长；g为间距比；L为方柱中心之间的距离；St为斯特劳哈尔数；f为涡脱落频率.

1.2 计算域及边界条件

三方柱布置形式及计算区域如图1所示.计算域为长方形，三方柱呈等边左“品”字型布置，上游为单方柱A，下游为双方柱B、C并列.方柱边长为无量纲边长D=1，A方柱形心至入流边界距离为20D，B、C方柱形心至出流边界的距离为40D，上下边界距离最近方柱中心为10D.入口为速度边界条件，来流速度为无量纲数U=1，出口取自由出流边界条件，上下壁面和方柱表面为Wall边界条件，参见图1.

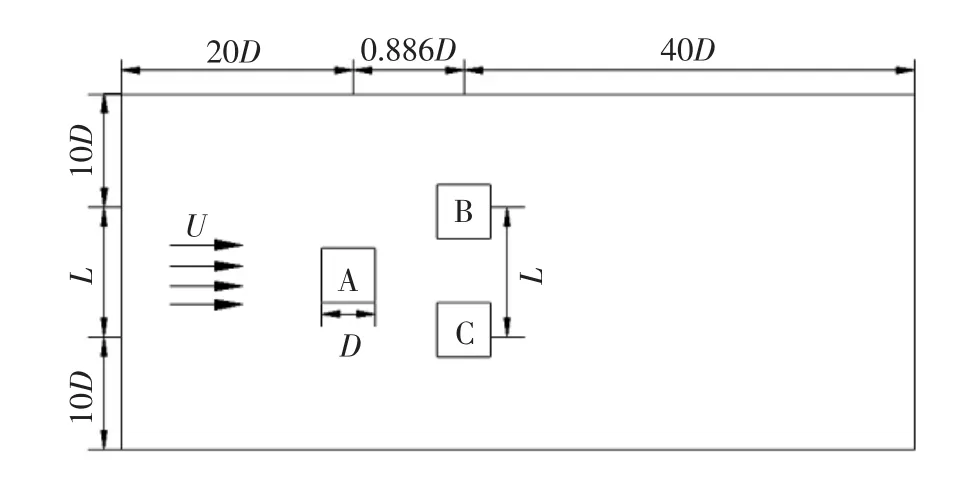
图1 等边三方柱布置形式及计算域示意

1.3 网格划分

在柱体绕流中，柱体周围靠近柱体的地方需要更高的求解精度.为了保证本研究的求解精度，验证算例的网格划分采用以下形式：在方柱外围划分一层越靠近方柱越密的矩形网格，目的是在数值模拟过程中，保证流体参数变化最为激烈的区域的求解精度；再在这层矩形网格的外围用非结构三角形网格对求解区域进行划分，并通过确定边界网格节点的方式，控制网格的疏密程度，越靠近柱体的地方网格越致密，如图2所示.为了加快收敛过程，时间导数项采用了二阶隐式离散格式.

图2 方柱网格划分示意

2 结果与讨论

2.1 验证算例

选取雷诺数为100、200时的单方柱绕流算例，与经典的计算和实验结果进行比较，验证本文所采用的数值方法和求解参数的有效性.表1为本文计算的时间平均阻力系数和斯特劳哈尔数与相关文献中的数值计算和实验结果的比较.从表1可以看到，本文的计算结果与经典结果比较吻合，证明本文的数值方法是合理有效的.

表1 单方柱绕流模拟结果比较

2.2 流动特性

对雷诺数为100、200的左品字三方柱绕流流场进行模拟，并进行间距比局部加密模拟.图3-4为t=300 s、Re为 100和 200时间距比 g分别为 1.2、1.5、2.0、2.5、3.0、3.5、4.0、4.5、5.0、5.5、6.0 下的涡量图.

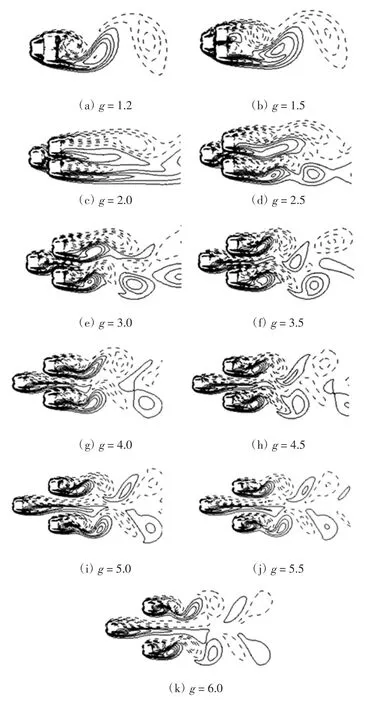
图3 Re为100时不同间距比的涡量图

由图3可知：当g≤1.5时，三方柱非常接近，此时流场形态类似于一个大的孤立方柱，在尾流区形成一组漩涡；当g＞1.5时，上流柱体脱落的剪切层附着于下流方柱，出现偏流现象，方柱B、C后产生了各自的漩涡，漩涡脱落发生在一个方柱后；两方柱之间的间隙流呈现出双稳态偏流现象；在g为2.0～3.0时，流场十分不稳定，在方柱A后出现了回流区，漩涡发生脱落；随着g进一步增大，偏流现象减弱；在g为3.5～4.5之间时，漩涡发生相位的相对偏移，上述现象与文献[1]的现象大致相同；当g≥5.0时，方柱B和C后的漩涡却呈现出反相位脱落；当g=6.0时，三方柱后产生各自漩涡，相互之间几乎不再有影响.

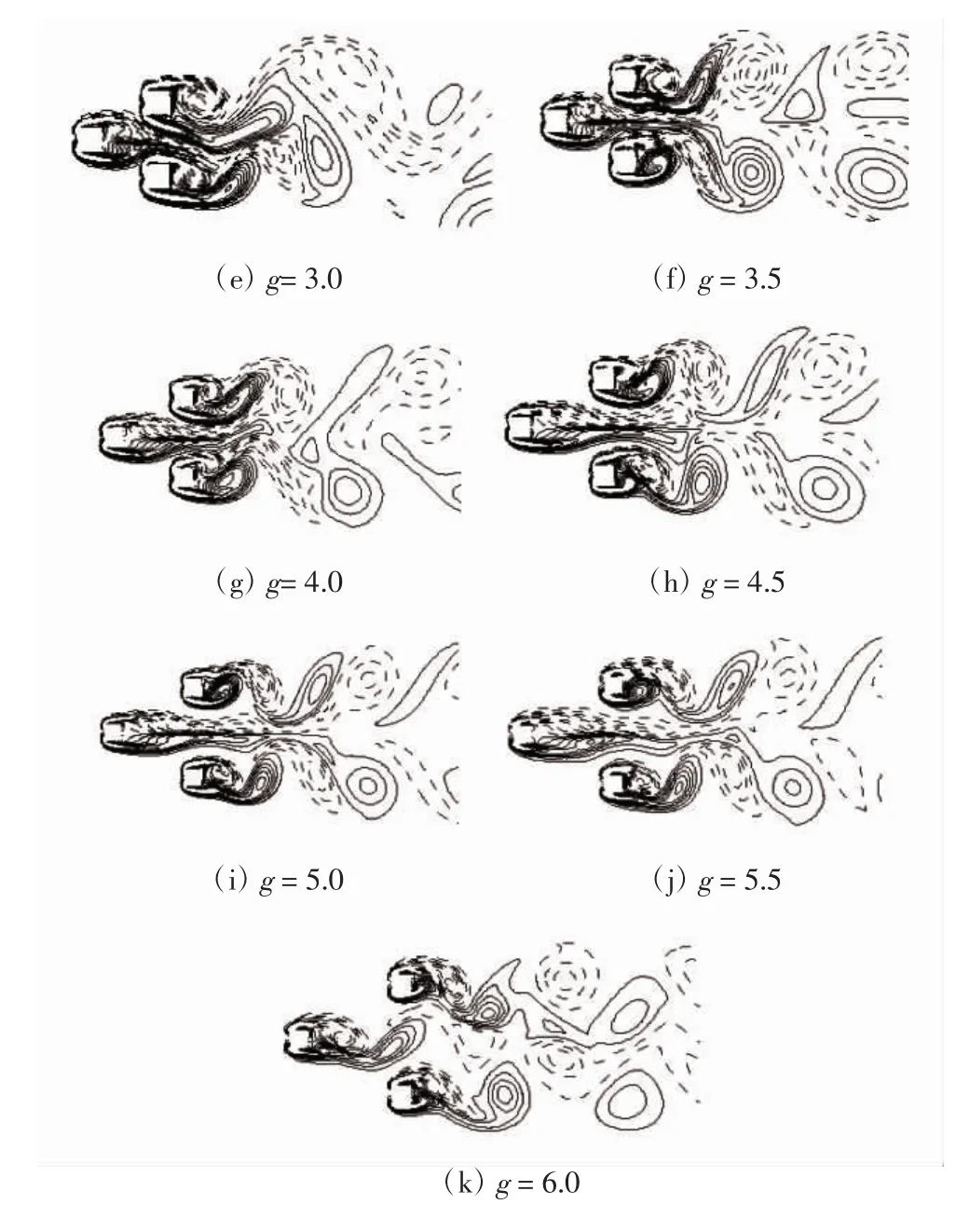
图4 Re为200时不同间距比的涡量图

由图4可知：当g=1.2时，已经出现偏流现象，间隙流对方柱的影响较大，方柱B、C后差生了各自的漩涡，漩涡脱落发生在一个方柱后，两方柱之间的间隙流呈现出双稳态偏流现象；在g为2.0～3.0时，流场十分不稳定，在方柱A后出现了回流区，漩涡发生脱落，偏流现象逐渐增强，这是因为随着g进一步增大，间隙流对后方对称的方柱B、C影响趋于相同，同时前方柱A与后方柱B、C之间流场的相互干扰逐渐减小，偏流现象慢慢减弱；当g=3.5时，下游方柱后的漩涡出现反相位脱落，流场为同步对称结构，偏流现象消失；在g为4.5～5.5之间时，漩涡始终处于反相位同步脱落；当g=6.0时，三方柱后产生各自漩涡，相互之间干扰现象并未消失.

2.3 Re为100时阻力系数和升力系数特性

图5给出Re=100时平均阻力系数CD随g的变化曲线.由图5可知：①在g为1.2～1.8区间内，上游方柱A所受的阻力略大于下游方柱B、C所受的阻力；当g=1.5时，方柱B、C的CD差值最大；②当g=2.0时，方柱A的CD值出现了最小值CD，A=1.10（这里下标表示具体的方柱，下同）；当g＞2.0时，三方柱的CD随 g 的增加而增大，之后随着 g 的增大，CD，B、CD，C始终大于 CD，A；g=2.5 时，CD，B=1.63，CD，C=1.60，接近于单方柱 CD，CD，A=1.22 依然小于单方柱 CD；③在 g＞3.0 时，B、C柱CD几乎相等，平缓变化，这与流线图中的变化相吻合；当g=4.0时，下游方柱B、C的CD约为单柱绕流时的1.15倍，与文献[1]的1.17倍大致相同；当g达到最大值5.5时，各柱的CD也分别达到最大值，CD，A=1.46，CD，B=1.89，CD，C=1.89，上游柱 A 的 CD，A依然小于单方柱绕流时的CD=1.61，下游B、C柱的CD比单方柱绕流的情形大.

图5 Re为100时CD-g的变化曲线

图5中的现象出现的原因主要是：①g过小时，A的自由剪切层会将下游的方柱B、C完全包围，来流阻力将主要作用在柱A上；②随着g的增加，下游方柱B、C已不再全部被上游柱A的自由剪切层吞没，来流会部分撞击到方柱B、C上；③g继续增大，B、C柱的来流阻力减小，而上游柱A的来流阻力增大，并未超过单柱绕流的数值；即使g较大，方柱A与方柱B、C之间区域的压力也远大于单柱绕流的情形，是由于下游并列方柱B、C的“夹心”效应.

图6给出Re=100时平均升力系数CL随g的变化曲线.

图6 Re=100时CL-g的变化曲线

由图6可以看出：上游方柱A的CL，A始终接近于常数0，与单方柱的CL一致（CL=-0.001），这表明下游方柱B、C周围的流动对上游柱A周围的流场已基本无干扰；下游方柱 B、C 的 CL，B和 CL，C大小几乎相等，方向相反，这表明柱体间具有更加强烈的横向干扰效应；其中g=1.5时，方柱A的CL，A突然增大，达到最大值；随着 g 的增加，CL，B和 CL，C对称地趋近于 0.综合分析绕流流场和CL变化规律可以推测，临界间距比应该在3.5附近.

2.4 Re为200时阻力系数和升力系数特性

图7给出Re=200时CD随g的变化曲线.

图7 Re=200时CD-g的变化曲线

由图7可以看出，Re为200时各方柱CD随g的变化比100时的剧烈：①在g为1.2～1.8区间内，上游方柱A所受的阻力略大于下游方柱B、C所受的阻力，两种雷诺数下的变化趋势一致；当g=1.5时，柱B、C的 CD差值最大；当 g=2.0 时，CD，A=1.08（这与 Re 为100时，当g=1.9时，柱A的CD值出现了一个下跌CD，A=1.10 相似），之后随着 g 的增大，CD，B、CD，C始终大于 CD，A；②随 g的增加，三方柱的 CD增大（g=1.9 除外）；当 g=2.2 左右时，CD，B、CD，C接近于单方柱阻力系数，CD，A依然小于单方柱阻力系数，这与Re为100时g=2.5处的现象相似；随后随着g的增加，三方柱的CD均增大，但A方柱的CD依然小于单方柱阻力系数；③在g=3.5时，CD突然增加，随后降低，平缓变化，这与Re为100时，在g=3.7处的变化相似，这与流线图中的突变相吻合；当g=3.5时，B、C柱的CD也分别达到最大值，CD，B=2.15，CD，C=2.19，显然，CD，A＞CD，B≈CD，C＞CD=1.63.

图8给出Re为200时CL随g的变化曲线.

图8 Re=200时CL-g的变化曲线

由图8可以看出：Re为200时CL随g的变化比Re为100时的变化剧烈；上游柱A的CL，A始终与单方柱的平均升力系数（CL=0.004）一致，接近于常数0，这表明下游方柱B、C周围的流动对上游柱A的流场几乎没有影响；下游并列的柱 B、C 的 CL，B和 CL，C大小几乎相等，方向相反，这表明柱体间具有更加强烈的横向干扰效应，这与Re为100时相似；其中g=3.5时，CL，B和CL，C呈现大小相等、方向相反的对称趋势.综合绕流流场和CL变化规律可以推测，临界间距比在4.0附近.

2.5 临界间距比的验证

为准确捕捉到临界间距比的数值，分别对g=3.5（Re=100）和 g=4（Re=200）附近进行加密.图 9 给出了间距比加密区间内CD和CL随g的变化曲线.

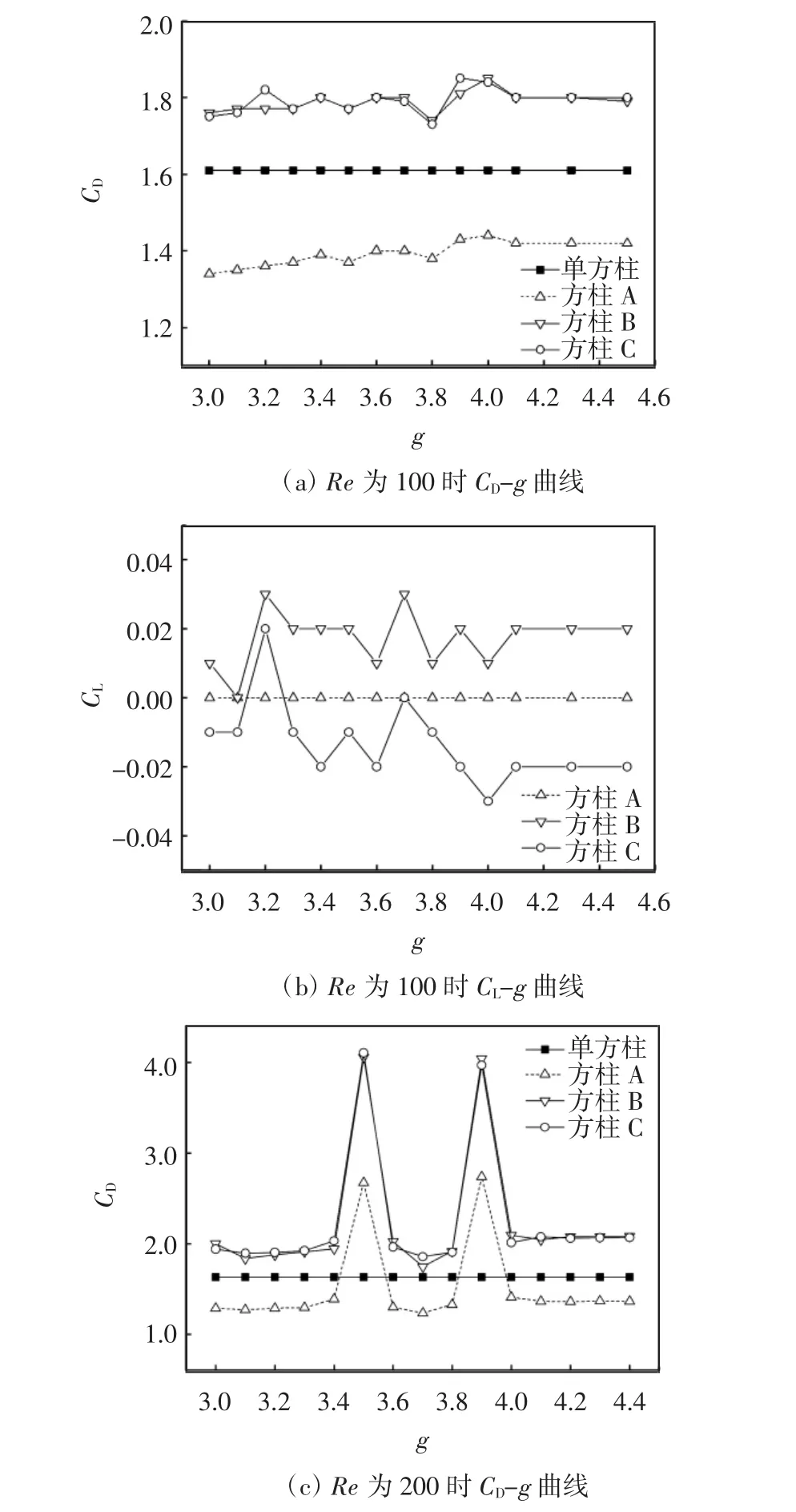
图9 不同Re时CD-g与CL-g的变化曲线

由图9a-9b可以看出：Re为100、g为3.0～4.5时，变化平缓，方柱A与方柱B、C的CD的变化趋势一致，CD，B=CD，C，CL，B=|CL，C|；由图 9c 可知，Re 为 200、g 为3.0～4.4，方柱A与方柱B、C的CD的变化趋势一致，在g为3.5与3.9时，三方柱CD突然增大.

图10 不同Re时St-g的变化曲线

图10给出斯特劳哈尔数St随g的变化曲线.由图 10a-10b中可以看出：Re为 100、g为2.0～3.0 之间时，St随g的增大变化幅度较大；随后，St趋于一致，随g的变化趋势与文献[2，13]基本相同，与单方柱绕流的 St=0.145接近；g≥3.5时，方柱 A、B、C 的 St与单方柱情形基本相等，在g=3.9处出现突然增大，方柱A、B、C的St几乎相等，这与CL变化趋势一致.说明此时三方柱之间的干扰最小，也就是柱B和柱C间偏流消失的原因；当g≥5.0时，三方柱之间的相互干扰现象消失.

由图10c-10d可以看出：Re为200、g=2.0～3.0之间，St随g的增大变化幅度较大；随后，St趋于一致，趋近单方柱绕流的St=0.163，与Re为100时的变化规律相似；g≥3.7时，方柱A、B、C的St几乎相等；g=4.1处出现突然增大；当g=6.0时，三方柱之间始终存在相互干扰现象.

图11 Re为100、g=3.7时流场涡量验证图

图11-12为临界间距比的流场涡量验证图，即Re为100、g=3.7、不同时间的涡量变化图11和Re为200、g=4.1、不同时间的涡量变化图12.

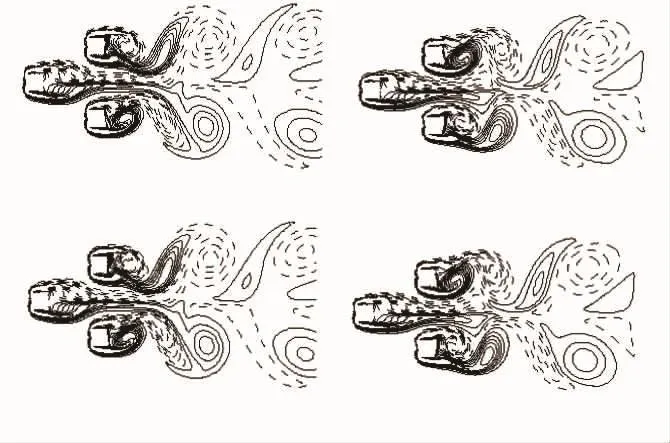
图12 Re为200、g=4.1时流场涡量验证图

综合分析图9-12可以确定，Re为100时，偏流现象消失的临界间距比g=3.7；Re为200时，偏流现象消失的临界间距比g=4.1.

3 结论

（1）当雷诺数Re为100、间距比g≥1.5时，出现双稳态间隙偏流；g≥2.5时，偏流现象减弱；当g=3.7时，方柱B、C后的漩涡出现同相位脱落现象，流场为同步对称结构，偏流现象消失；当g≥4.9时，方柱B、C后的漩涡出现反相位脱落现象；当g=5.0时，流场呈对称分布；当g≥5.0时，三方柱之间的相互干扰现象消失；偏流现象消失的临界间距比为3.7，且g=3.7时，方柱A、B、C的斯特劳哈尔数St出现突然增大，且几乎相等.

（2）当Re为200、g≥1.2时，出现双稳态间隙偏流；g≥2.5时，偏流现象减弱；当g=3.5时，方柱B、C后的漩涡出现反相位脱落现象，流场为同步对称结构，偏流现象消失；当g≥4.5时，方柱B、C后的漩涡却呈现出反相位脱落；在g为4.5～5.5之间，漩涡始终处于反相位同步脱落；当g=6.0时，三方柱之间始终存在相互干扰现象；偏流现象消失的临界间距比为4.1，且g≥4.1，方柱 A、B、C 的 St几乎相等.

（3）Re为200时的流场比100时的更不稳定，随着雷诺数的增加，偏流现象消失的临界间距比增大.

参考文献：

[1]余化军.圆柱和方柱绕流及矩形柱涡激振动的二维数值分析[D].天津大学，2011：41-45.

[2]张 伟，戴玉满.低雷诺数下等边布置三方柱绕流的数值研究[J].机械工程学报，2015（12）：185-191.

[3]OKAJIMA A.Strouhal numbers of rectangular cylinders[J].Journal of Fluid Mechanics，1982，123（123）：379-398.

[4]赵心广.三方柱绕流的大涡模拟及频谱分析[J].水科学与工程技术，2011（4）：28-30.

[5]郭明旻，黄东群，林 晨，等.三方柱表面风压脉动的时域特性[J].力学季刊，2001，22（4）：439-446.

[6]张爱社，张 陵.等边布置三圆柱绕流的数值分析[J].应用力学学报，2003，20（1）：31-36.

[7]王掩刚，陈俊旭，先松川.基于POD方法的二维方柱低雷诺数绕流流场分析研究[J].西北工业大学学报，2014（4）：612-617.

[8]DAVIS R W，MOORE E F，PURTELL L P.A numericalexperimental study of confined flow around rectangular cylinders[J].Physics of Fluids，1984，27（1）：46-59.

[9]SOHANKAR A，DAVIDSON L，NORBERG C.Numerical simulation of unsteady flow around a square two-dimensional cylinder[C]//The University of Sydney.Australasian Fluid Mechanics Conference.Sydney：The University of Sydney，1995：517-520.

[10]ISLAM S U，ZHOU C Y.Numerical simulation of flow around a row of circular cylinders using the lattice Boltzmann method[J].Information Technology Journal，2009，8（4）：513-520.

[11]SAHA A K，BISWAS G，MURALIDHAR K.Three-dimensional study of flow past a square cylinder at low Reynolds numbers[J].International Journal of Heat&Fluid Flow，2003，24（1）：54-66.

[12]WAN D C，PATNAIK B S V，WEI G W.Discrete singular convolution-finite subdomain method for the solution of incompressible viscous flows[J].Journal of Computational Physics，2002，180（1）：229-255.

[13]沈立龙，刘明维，吕启兵，等.双排并列三方柱绕流数值模拟[J].科学技术与工程，2014，14（23）：135-139.