带高斯噪声的受限玻尔兹曼机在变压器故障诊断中的应用❋

王鲁昆， 赵晓颖， 张 健， 田春鹏， 宿 浩， 唐功友

(1.中国海洋大学信息科学与工程学院，山东 青岛 2661001； 2. 山东科技大学信息工程系，山东 泰安 271021；3. 泰山医学院外国语学院，山东 泰安 271000)

变压器是电力网络运行过程中最重要的设备之一，变压器如果产生故障，会给电力网络带来巨大的经济损失。变压器的定期维修和故障及时发现具有重要的意义。目前用于检测变压器是否正常运行的方法很多，其中应用最为广泛的是油中溶解气体分析法(Dissolved Gas Analysis, DGA)。该方法是利用对变压器绝缘油中的五种溶解气体(H2、CH4、C2H6、C2H4和C2H2)浓度进行分析，从而确定变压器的故障类型[1]。

近些年研究者提出了基于机器学习变压器故障诊断方法，主要有基于模糊集理论[2]，基于支持向量机[3]，基于聚类分析法[4]，基于神经网络法[5-7]等。还有研究者提出基于进化理论的变压器故障诊断方法，主要有基于遗传方法[8]，基于粒子群方法[9]和基于免疫方法[10]等。这些算法在故障诊断中均取得较好的效果。

2006年由 Hinton 等人[11]，在Science杂志上提出深度信念网络(Deep Belief Network, DBN)模型，被称为神经网络的新生[12]。深度信念网络从结构上来说是由多个受限玻尔兹曼机(Restricted Boltzmann Machine, RBM)组成。Roux和Bengio[13]从理论上证明了，如果隐层的单元数量足够大，RBM能够拟合任意类型的离散分布。近些年基于RBM的深度算法在图像识别[14]，语音识别[15]，文本识别[16]等领域均取得了成功。然而应用RBM算法在变压器故障诊断领域的研究较为少见。本文基于深度结构的RBM算法与变压器油中DGA技术相结合进行变压器故障诊断。构造由两层RBM和一层BP所组成的深度信念网络DBN。利用RBM进行预训练并提取特征信息，利用BP计算误差并重构DBN。仿真结果表明该方法对变压器故障分类有较高的准确性。

1 变压器故障分类

电力变压器大多数都是用绝缘油实现绝缘和散热功能。电力变压器虽然经过密封和干燥处理，但是在运行过程中难免会混入少量空气。这些空气在热力和电力的作用下与绝缘油发生化学反应，产生少量CO、CO2以及一些低分子烃类。

变压器在正常运行的情况下，绝缘油内部的分子结构比较稳定，不会出现化学键的断裂从而产生烃类气体。如果内部发生故障，那么故障点会释放出大量的热量。这些热量就会迫使故障点周围的绝缘油裂变，从而产生CH4(甲烷)、C2H6(乙烷)、C2H4(乙烯)、C2H2(乙炔)、H2(氢气)，以及CO(一氧化碳)、CO2(二氧化碳)。某些情况下CO和CO2并不是由设备故障造成的。 因此CH4、C2H6、C2H4、C2H2、H2这五种气体就成为检测变压器故障的特征气体[17]。绝缘油的烃分子在300～400 ℃的时候开始发生裂变反应。随着温度的不断增加，H2和烃类气体的含量也会增加，裂变气体的热解顺序为：烷烃-烯炔-炔烃。变压器内部故障主要有机械、热、电三种模式。典型的变压器故障可以概括为局部放电、低能放电、高能放电、低温过热、高温过热这五类。当产生故障时，五种特征气体的含量呈现一些规律性，比如当局部放电时，如果放电密度较低时总烃类含量比较低，H2含量通常会占到总量的90%以上。

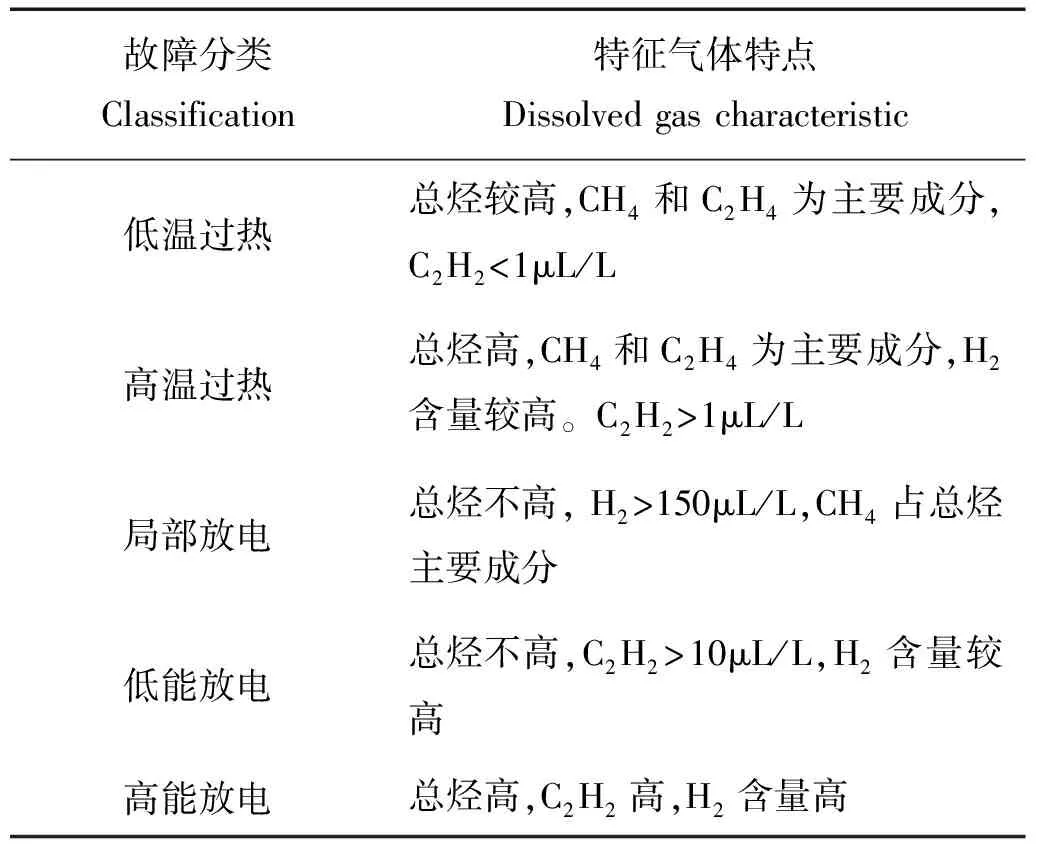
表1 判断故障性质方法Table 1 Method of diagnose fault characteristic

当溶解气体超过正常值范围时候，可用表1判断故障性质。在故障诊断的时候，特征气体的含量与故障类型有着十分密切的联系。因此用特征气体含量来判断变压器故障性质比较方便直观。

由于不同的故障所含有的特征气体的含量差别较大，一般来说通过对气体的相对含量的统计更加准确，更容易诊断故障类型。因此三比值法，即W(CH4)/W(H2)、W(C2H2)/W(C2H4)、W(C2H4)/W(C2H6)数据往往被用来进行故障分析。

2 模型设计

根据DBN的设计原理，网络结构设计采用两层RBM和一层BP的模式。可见层包含3个单元，用来存放输入的变压器故障三比值的数据。输出层T包含5个单元，用来存放三比值数据对应的变压器故障类型。在维数较低的情况下，神经网络每层的单元格数k可以利用kolmogorov定理计算

(1)

其中：n是可视层单元个数；m为输出层单元个数；a为1～10的随机整数；[·]表示取整。利用式(1)和实际仿真确定第一个隐层H0含有5个单元，第二个隐层H1含有7个单元。另外每层增加一个偏置项，用来存放阈值。可见层V和隐层H0从逻辑结构上组成第一层RBM，隐层H0和隐层H1共同组成第二层的RBM，隐层H0看做是第二层RBM的输入。隐层H1和输出层T在逻辑上组成第三层BP，隐层H1看做是第三层BP的输入。网络结构图如图2所示。

两层RBM网络状态{v,h0,h1}的能量模型可以定义为

(2)

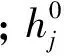
(3)

根据联合概率分布，计算求得条件概率分布为

(4)

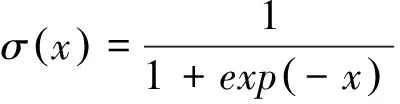
由于在可见层单元之间没有直接的链接，并且只与隐层h0关联。因此可见单元之间符合独立条件分布，且条件项为h0。条件概率分布为

(5)

同理隐层h1的条件概率分布为

(6)

通过最大化训练样本的极大似然对数函数来求解θ

(7)

对(θ)求偏导得到

(8)

由于进一步求导时P(h0,h1,v|θ)分布难以获得，所以通过CD算法近似计算其分布。

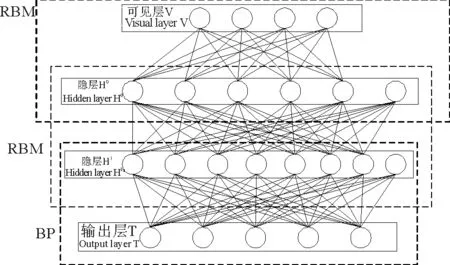
图1 网络结构图Fig.1 The structure of neuro network

CD算法就是利用Kullback-Leibler 距离来计算概率分布的区别性。

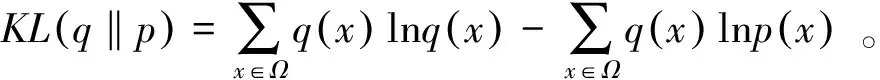
(9)

利用式(9)计算采样概率分布的区别性

KL(p0‖p∞)-KL(pn‖p∞)，

(10)

其中：p0是初始状态的联合概率分布；pn是经过n步MCMC采样以后的联合概率分布；p∞是马氏链最末端的联合概率分布。CD算法就是不断的将pn赋值给p0，通过对参数的修正，让KL距离趋近与0。CD算法的精准度近似于MCMC方法[18]，更新参数由下式计算

Δai=ε([vi]data-[vi]recon)，

(11)

其中：ε表示网络学习率；[·]recon表示重构以后的概率分布。基于CD算法的RBM训练的主要步骤如下：

Step 1 初始化令ΔWij、ΔWjk、Δai、Δbj、Δck的值为0，Wij、Wjk、ai、bj和ck随机较小的数。然后设置迭代次数E。

Step 2 将训练样本v赋值给的v0利用式(5)、式(6)计算h0、v1、h1。

Step 3 利用式(11)，计算ΔWij、ΔWjk、Δai、Δbj、Δck的值，并更新参数θ←θ+Δθ。

Step 4 如果迭代次数小于E，则重复Step 2, 否则结束。

3 训练与仿真

变压器油中特征气体的浓度数据，对分析变压器故障有着直接的指导意义。根据收集到的数据进行整理，训练数据分为两个部分，一部分为输入数据，即五种特征气体H2、CH4、C2H2、C2H6、C2H4的样本数据，利用三比值法[19]计算出三个比值的数据，作为测试样本的输入数据。也就是说训练输入样本为三维矩阵。为了减小数据的奇异性，提高训练速。使用数据归一化公式，把训练输入样本的数据归一到[-1,1]之间。

(12)

其中：y表示归一化处理后的样本数据，令ymax=1，ymin=-1；xmax为样本中最大值，xmin为样本中的最小值。

训练数据的另外一部分为输出数据，即特征气体的样本数据对应的故障情况，将变压器的故障分为5类，低温过热(00001)、高温过热(00010)、局部放电(00100)、低能放电(01000) 和高能放电(10000)。

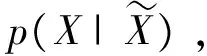
训练网络的过程中，一些参数的设置是十分重要的。近来的一些研究表明[20]，如果参数设置不当，会影响最终的实验结果。根据经验和在仿真过程中的一些调试，笔者对一些重要的参数做了如下设置。

学习率设置：学习速率的选取很重要，过大会导致系统不稳定，过小会导致训练周期过长、收敛慢，达不到要求的误差。一般倾向于选取较小的学习速率以保持系统稳定，通过观察误差下降曲线来判断。下降较快说明学习率比较合适，若有较大振荡则说明学习率偏大。由于网络规模大小的不同，学习率选择应当针对其进行调整。在本实验中，设置网络的学习率为0.05，此设置收敛速度快，误差曲线波动小。

动量项设置：为了避免受学习率设置影响，在参数更新的时候，增加动量项的设置，使得参数的变化并不完全由似然函数的梯度方向决定。避免了出现过度拟合的问题。在本试验中设置动量项为0.9。

本文以IEC TC 10 Database[21]所提供的134组历史故障案例样本资料作为变压器故障的输入样本。使用K层交叉验证(K-fold)的方式对实验数据进行分类。实验数据分为K组，交叉验证过程重复K次，每次选取其中一个不同的部分作为测试数据，其余K-1组作为训练数据。实验设置K=9，即将数据分为9组。每次选取其中一组作为测试数据，其余8组作为训练数据，重复9次，确保每组数据都被当做测试数据。最终把测试结果取平均值即可得到整体正确率。图3为经过BP训练的误差曲线图与经过RBM训练的误差曲线图，图中可以发现RBM的误差明显小于BP训练的误差，并且收敛速度更快。经过1 000轮回的训练后，误差能够达到10-2左右。图4为带高斯噪声和不带高斯噪声的RBM的误差曲线图。如图可以看出，增加部分高斯噪声以后，曲线的收敛速度更快。在同样学习率的情况下，训练效果更优。

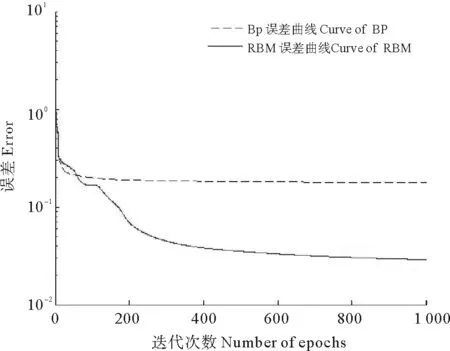
图2 BP与RBM误差曲线图Fig.2 The error curve of BP and RBM

为了验证算法有效性，本文设计BP、K邻近(K-NearestNeighbor, K-NN)、支持向量机(Support Value Machine, SVM)和RBM几种算法的对比试验。表2所示为K-NN算法的识别率，K=15时，正确率最高为90%。表3所示为SVM在选择不同核函数(Kernel Function, KF)的情况下的正确率，当选择径向基函数(Radial Basis Function, RBF)作为核函数时，正确率最高为79.9%。

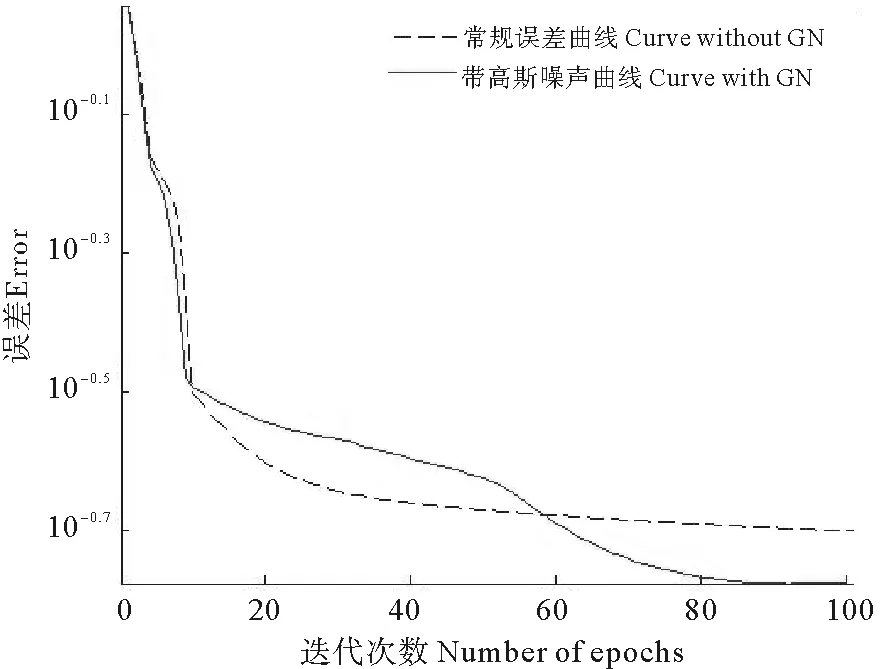
图3 带高斯噪声与不带高斯噪声误差曲线图Fig.3 The error curve of with Gaussian Noise and without Gaussian Noise

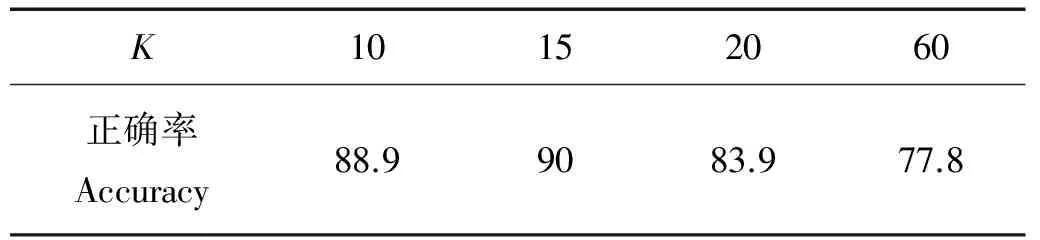
Table 2 Classification accuracy of K-NN /%

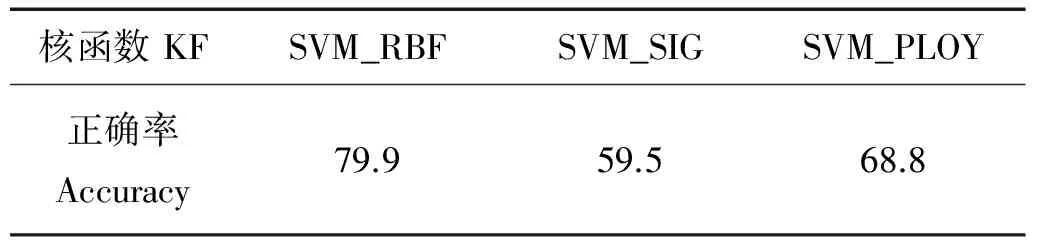
表3 SVM分类正确率Table 3 Classification accuracy of SVM /%

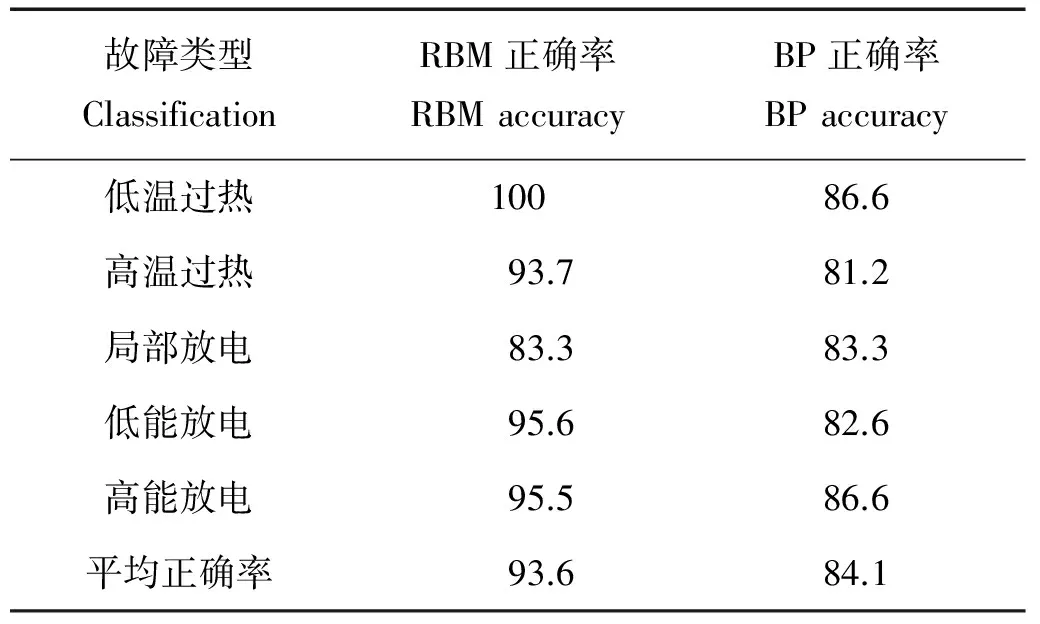
表4 BP和RBM算法结果比较Table 4 Classification accuracy of BP and RBM /%

通过对134组训练数据进行了1 000轮回的训练后，表4列举了BP和RBM的明细正确率。BP算法平均正确率为84.1%。RBM算法在低温过热分类中获得100%的正确率，在局部放电分类中获得最低83.3%的正确率，平均正确率为93.6%。

在已经训练好的网络基础上，本文对10组测试样本进行了检验。使用RBM网络训练结果与实际的故障结果进行比较如表5所示。可以看出，使用RBM网络诊断的结果与变压器的实际故障具有较高的吻合度。

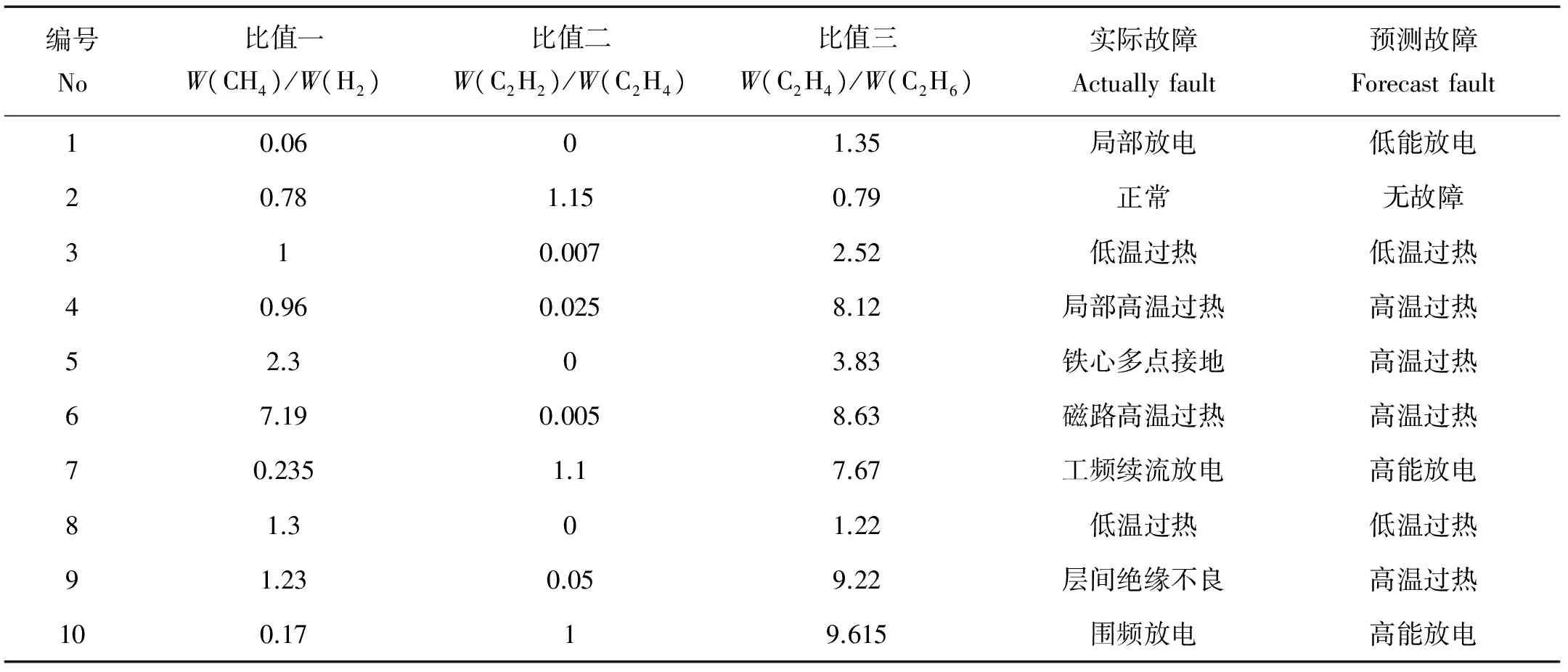
表5 训练结果Table 5 The training results

4 结语

本文研究了一种基于受限玻尔兹曼机模型的变压器故障诊断方法。方法首先根据变压器绝缘油中五种特征气体含量计算三比值数据。然后构造一个由两层RBM和一层BP所组成的DBN网络。利用RBM预训练样本数据，利用BP进行误差计算并判断故障类型。仿真结果验证该方法的有效性。

参考文献：

[1] 刘勇辉. 基于DGA的变压器故障诊断[J]. 高电压技术, 2005, 31(6): 87-88.

Liu Yonghui. Power Transformer fault diagnosis based-on dissolved gas analysis[J]. High Voltage Engineering, 2005, 31(6): 87-88.

[2] 杜文霞, 句希源, 吕锋. 基于模糊聚类算法的变压器故障诊断研究[J]. 变压器, 2009, 46(8): 65-69.

Du Wenxia, Ju Xiyuan, Lu Feng. Research on transformer fault diagnosis based on fuzzy clustering algorithm[J]. Transformer, 2009, 46(8): 65-69.

[3] 郭创新, 朱承治, 张琳, 等. 应用多分类多核学习支持向量机的变压器故障诊断方法[J]. 中国电机工程学报, 2010, 30(13): 130-136.

Guo Chuangxin, Zhu Chengzhi, Zhang Lin, et al. A fault diagnosis method for power transformer based on multiclass multiple-kernel learning support vector machine[J]. Proceedings of the CSEE, 2010, 30(13): 130-136.

[4] 符杨, 田振宁, 江玉蓉, 等. 加权模糊核聚类法在电力变压器故障诊断中的应用[J]. 高电压技术, 2010, 36(2): 371-374.

Fu Yang, Tian Zhenning, Jiang Yurong, et al. Power transformer fault diagnosis using weighted Fuzzy kernel clustering[J]. High Voltage Engineering, 2010, 36(2): 371-374.

[5] 付强, 陈特放, 朱佼佼. 采用自组织RBF网络算法的变压器故障诊断[J]. 高电压技术, 2012, 38(6): 1368-1375.

Fu Qiang, Chen Tefang, Zhu Jiaojiao. Transformer fault diagnosis using self-adaptive RBF neural network algorithm[J]. High Voltage Engineering, 2012, 38(6): 1368-1375.

[6] 李霜, 王朗珠, 张为, 等. 基于DGA的改进BP神经网络的变压器故障诊断方法[J]. 变压器, 2010, 47(12): 61-65.

Li Shuang, Wang Langzhu, Zhang Wei, et al. Fault diagnosis method of transformer based on improved BP neural network of DGA[J]. Transformer, 2010, 47(12): 61-65.

[7] 王晓霞, 王涛. 基于BP神经网络的变压器故障诊断[J]. 华东电力, 2008, 36(2): 112-116.

Wang Xiaoxia, Wang Tao. Transformer fault diagnosis based on BP networks[J]. East China Electric Power, 2008, 36(2): 112-116.

[8] 潘翀, 陈伟根, 云玉新, 等. 基于遗传算法进化小波神经网络的电力变压器故障诊断[J]. 电力系统自动化, 2007, 31(13): 88-92.

Pan Zhong, Chen Weigen, Yun yuxin, et al. Fault diagnosis of power transformers based on genetic algorithm evolving wavelet neural network[J]. Automation of Electric Power Systems, 2007, 31(13): 88-92.

[9] Tang W H, Goulermas J Y, Wu Q H. A probabilistic classifier for tr-ansformer dissolved gas analysis with a particle swarm optimizer[J]. IEEE Transactions on Power Delivery, 2008, 23(2): 751-759.

[10] 宋绍民, 王耀南, 孙炜, 等. 基于免疫聚类算法的变压器DGA数据故障诊断方法[J]. 变压器, 2008, 45(8): 70-72.

Song Shaomin, Wang Yaonan, Sun Wei, et al. Fault diagnosis method with transformer DGA data based on immune recognition algorithm[J]. Transformer, 2008, 45(8): 70-72.

[11] Hinton G E, Salakhutdinov R R, Reducing the dimensionality of data with neural networks[J]. Science, 2006, 313(5786), 504-507.

[12] Garrison W. Cottrell. New life for neural networks[J]. Science, 2006. 313: 454-455.

[13] Roux N L, Bengio Y. Representational power of restricted boltzmann machines and deep belief networks[J]. Neural Computation, 2008, 20(6): 1631-1649.

[14] Salakhutdinov R, Larochelle H. Efficient learning of deep Boltzmann machines[J]. Journal of Machine Learning Research: Proceedings Track, 2010, 9(1): 693-700.

[15] Jaitly N, Hinton G E. Learning a better representation of speech sound waves using restricted Boltzmann machines[C]. Proc of the 2011 IEEE Int Conf on Acoustics. Speech and Signal Processing, 2011: 5884-5887.

[16] Dahl G, Yu Dong, Deng Li, et al. Context-dependent pretrained deep neural networks for large vocabulary speech recongnition[J]. IEEE Trans on Audio, Speech and Language Processing. 2012, 20(1): 30-42.

[17] 耿基明, 郭晓峰. 应用变压器油色谱分析判断变压器故障[J]. 变压器, 2006, 43(11): 44-47.

Geng Jiming, Guo Xiaofeng. Diagnosis of Transformer Faults by Chromatogr aphic Analysis of Transformer oil[J]. Transformer, 2006, 43(11): 44-47.

[18] Hinton G E. Training products of experts by minimizing contrastive divergence [J]. Neural Computation, 2002, 14(8): 1771?1800.

[19] 尚勇, 闫春江, 严璋. 基于信息融合的大型油浸电力变压器故障诊断 [J]. 中国电机工程学报, 2002, 22(7): 50 -55.

Shang Yong, Yan Chunjiang, Yan Zhang. Synthetic Insulation Fault Diagnostic Model of Oil-immersed Power Transformers Utilizing Information Fusion[J]. Proceedings of the CSEE, 2002, 22(7): 50 -55.

[20] Schulz H, Müller A, Behnke S. Investigating Convergence of Restricted Boltzmann Machine Learning[C]. //NIPS 2010 Workshop on Deep Learning and Unsupervised Feature Learning, 2010: 1-9.

[21] Duval M, dePabla A. Interpretation of gas-in-oil analysis using new IEC publication 60599 and IEC TC 10 databases[J]. IEEE on Electrical Insulation Magazine, 2001, 17: 31 -41.