基于ECC的具有前向安全性的VSS方案
2018-04-13韦性佳张京花芦殿军
韦性佳,张京花,芦殿军
(青海师范大学 数学与统计学院,青海 西宁 810008)
0 引 言
秘密共享作为一种基础的密码学手段,在信息安全方面扮演着非常重要的角色。自从1979年Shamir[1]提出基于拉格朗日插值多项式门限秘密共享方案之后,有关秘密共享方面的研究受到了广大研究者的高度关注。
1985年Chor等[2]提出了可验证的秘密共享方案(VSS)的理念。1992年Pedersen[3]在前人的基础上提出了一种更为简洁、实用的VSS方案。起初的VSS方案存在计算量大、效率相对较低等缺陷,直到Neal Koblitz等[4]发现有限域上椭圆曲线离散对数问题是难解的以后,椭圆曲线(elliptic curve,ECC)以它计算量小、效率高等优势迅速成为密码学研究的一个重要工具。
1989年,Brickell[5]提出了一种基于向量空间存取结构的秘密共享方案。在这方面,张福泰等[6-8]基于双线性变换提出的秘密共享方案对文中的研究具有重要的启发作用。
1997年,Anderson[9]提出了前向安全性(forward security)理论,该理论可以有效地减少因为秘密泄露对系统安全所带来的隐患。在此基础上,1999年Bellare[10]提出了一种前向安全的数字签名方案。近年来,王彩芬等[11]提出了具有前向安全性的秘密共享方案,基于有限域上离散对数难解问题和强RSA假设[12-13],有效地实现了秘密的前向安全性,并且该方案具有很强的实践价值。
在已有秘密共享方案[14-16]研究成果的基础上,文中提出了一种基于ECC的具有前向安全性质的VSS方案。该方案利用椭圆曲线计算量小、效率高的优点,同时充分发挥前向安全理论在秘密保护方面的优势,为秘密共享方案提供了双重的安全保障。同时该方案是基于向量空间的存取结构,在秘密的重构中更加安全、有效。
1 基础知识
1.1 椭圆曲线离散对数问题(ECDLP)
给定有限域GF(q)上的椭圆曲线E,生成元P∈E(GF(q)),阶q,∀Q∈〈P〉,寻找a∈[0,q-1],使得Q=aP,称为椭圆曲线离散对数问题。
1.2 前向安全性理论
前向安全性理论(forward security theory)具体分析如下:
(1)Hi(i=1,2,…,n)将S的有效期分为T(1,2,…,T)个时间段;
(2)在整个有效期内,公钥PKU不变,但第j个时间段私钥SKU随着时间段j的改变而改变;
(3)在第j个时段,Hi计算Sj=f(Sj-1),其中f是一个单向函数;
(4)算出Sj后,立即删除Sj-1,这样即使攻击者A获得了第j个时间段的Sj后也不能获得关于S0,S1,…,Sj-1的任何信息。
1.3 系统中的记号与参数
H:参与者集合;
Hi:第i个参与者(Hi∈H,i=1,2,…,n);
D:可信中心,且D∉H;
S0:初始秘密;
Sj:第j个时间段的秘密;
T:时间周期;



1.4 向量空间存取结构

2 提出的方案
2.1 系统初始化

然后,D广播ψ(D),且将ψ(Hi)发送给Hi(i=1,2,…,n)。

初始子秘密Si0=(A+B)·ψ(Hi)=Ki0+Ri0(i=1,2,…,n),其中Ki0=ψ(Hi)·A=ai1(P+x1Q)+…+ait(P+xtQ)=a1A1+…+atAtRi0=ψ(Hi)·B=ai1(P+x1R)+…+ait(P+xtR)=ai1B1+…+aitBt。
E0=gK0+hR0,Ej=gAj+hBj后,D广播g,h,E0,Ej(j=1,2,…,t),且通过秘密信道将(Ri0,Ki0),Si0发送Hi(i=1,2,…,n)。
(3)第j个时间段的共享秘密Sj=2j(A+B)·ψ(D)(j=0,1,…,T)
2.2 子秘密更新
令Sij=2Si(j-1)(i表示第i个参与者,j表示第j个时间段)。
注:(1)每个成员Hi通过非交互式的方式来更新自己在第j个时间段的子秘密;
(2)当更新Sij后,立即删除Si(j-1)。
2.3 秘密的验证
2.3.1 初始阶段秘密的验证
(1)验证可信中心D的正确性(初始阶段)。
对于任意一个参与者Hi,通过式(1)来验证可信中心D的正确性:
(1)
(2)参与者Hi通过式(2)验证可信中心D发送给自己的信息的正确性:
(2)
2.3.2 验证更新秘密
D计算S=h1(2T+1S0),SPi=h1(2T+1Si0)(i=1,2,…,n),并广播S,SPi。
(1)用户Hi验证自己在第j个时间段的子秘密进化是否有效。
每个成员Hi检验:
h1(2T+1-jSij)=SPi
(3)
若式(3)成立,则Hi证明自己在第j个时间段的子秘密进化是有效的。
(2)合格子集验证第j个时间段所恢复的秘密Sj是否正确。
h1(2T+1-jSj)=S
(4)
若式(4)成立,则合格子集可以确定在第j个时间段恢复的共享秘密Sj是正确的。
2.4 秘密的恢复
任意一个授权子集(成员个数必须≥t)联合起来,利用每个成员的秘密份额可以恢复秘密,其过程为:
(1)为不失一般性,取重构成员H={H1,H2,…,Ht},这t个成员利用ψ(Hi),根据向量空间存取结构,有如下等式:
ψ(D)=ψ(H)·CT
(5)
其中,C=(c1,c2,…,ct);ψ(H)={ψ(H1),ψ(H2),…,ψ(Ht)}。
然后利用式(5)解出向量C。

3 安全性及正确性分析
3.1 方案的正确性
定理1:在初始阶段,式(1)可验证可信中心D的正确性,式(2)可验证D发给参与者Hi的信息的正确性。
证明:根据已知条件Ej=gAj+hBj,代入等式右侧,则有:
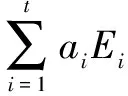
g(a1A1+…+atAt)+
h(a1B1+…+atBt)=
gK0+hR0=E0
由此可得E0,Ej(j=1,2,…,t)是正确的。
同理可证式(2)成立,如下:

(gA1+hB1)ai1+(gA2+hB2)ai2+…+
(gAt+hBt)ait=g(ai1A1+…+aitAt)+
h(ai1B1+…+aitBt)=
gKi0+hRi0
因此D发给参与者Hi的信息是正确的。
定理2:方案中子秘密更新阶段的验证过程是正确的,即:式(3)、式(4)是正确的。
证明:Sij=2jSi0
h1(2T+1-jSij)=h1(2T+1-j·2jSi0)=h(2TSi0)=SPi
即式(3)成立,则说明子秘密的更新是正确的。
同理
Sj=2j(A+B)·ψ(D)=2jS0
h1(2T+1-jSj)=h1(2T+1-j·2jS0)=S
即等式(4)成立,说明合格子集恢复的共享秘密是正确的。
3.2 方案的安全性
定理3:系统中的公开信息不会揭示关于共享秘密Sj与子秘密Sij的任何信息。

定理4:只有有效的合格子集(成员个数必须≥t)方能构造出秘密Sj。
证明:根据向量空间存取结构的定义,不失一般性地取重构成员为H1,H2,…,Ht,于是有:ψ(D)=c1ψ(H1)+…+ctψ(Ht)。
如果秘密重构成员的个数小于t,根据线性方程组的性质,方程组(6)的解不唯一,即存在无穷多个解,则要解出系数c1,c2,…,ct是不可行的,所以至少需要t个合格成员联合起来,方能解下列方程组:
(6)
计算出系数c1,c2,…,ct后,利用式(7)计算并恢复出在第j个时间段的秘密。
Sj=2j(A+B)ψ(D)=
2j(A+B)(c1ψ(H1)+…+ctψ(Ht))=
c12jS10+c22jS20+…+ct2jSt0=
c1S1j+c2S2j+…+ctStj
(7)
定理5:方案具有前向安全性。
证明:该方案所具有的前向安全性具体体现在参与者所持子秘密的前向安全性及秘密信息的前向安全性。
在子秘密的更新阶段,假设敌手通过某种方式获得参与者Hi在第j个时间段的子秘密Sij,若要计算Sik(k=1,2,…j-1),由于子秘密是参与成员通过非交互的方式更新产生的,并且参与者在更新子秘密后,立即删除了前一时间段的秘密。所以即使敌手掌握了第j个时间段的子秘密Sij,要想破解前j个时间段内的子秘密就必须面对椭圆曲线离散对数的难解问题,这样就保障了子秘密的前向安全性。
同理即便攻击者得到了第j个时间段的秘密Sj=2j(A+B)·ψ(D),若要通过Sj计算Sk(k=1,2,…,j-1),他将面临同样的问题。
4 方案的计算成本
设ρ代表G1中的标量乘法运算,结果如表1所示。该方案的运行时间复杂度为O(n),即在多项式时间范围内。说明方案的计算成本较低。

表1 方案的计算量分析
5 结束语
在文献[6,11]的基础上,基于向量空间存取结构提出了一种具有前向安全性的秘密共享方案,无论是在系统的安全性方面,还是在计算效率方面都有一定的提升。如果秘密在被动泄露的情况下,该方案可以避免秘密持有者的抵赖行为,检查出欺诈行为,同时该方案利用前向安全性理论保障了系统的前向安全性。
参考文献:
[1] SHAMIR A.How to share a secret[J].Communication of the ACM,1979,22(11):612-613.
[2] CHOR B,DOLDWASSER S,MICALI S,et al.Verifiable secret sharing and achieving simultaneity in the presence of faults[C]//Proceedings of the 26th IEEE symposium on foundations of computer sciences.Washington,DC,USA:IEEE Computer Society,1985:383-395.
[3] PEDERSON T P.Non-interactive and information-theoretic secure verifiable secret sharing[C]//Proceedings of the 11th annual international cryptology conference on advances in cryptology.London,UK:Springer-Verlag,1992:129-140.
[4] NEAL K.Elliptic curve cryptosystems[J].Mathematics of Computation,1987,48(177):203-209.
[5] BRICKELL E F. Some ideal secret sharing schemes[J].Journal of Combinatorial Mathematics & Combinatorial Computing,1989,434:468-475.
[6] ZHANG F,ZHANG J.Efficient and information-theoretical secure verifiable secret sharing over bilinear groups[J].Chinese Journal of Electronics,2014,23(1):13-17.
[7] 张福泰.基于向量空间接入结构的分布式密钥生成[J].电子学报,2005,33(5):816-819.
[8] 张福泰,王育民.适用于任意接入结构的可验证多秘密分享方案[J].通信学报,2007,28(11):59-64.
[9] ANDERSON R. Two remarks on public-key cryptology[C]//Fourth ACM conference on computer and communications security.[s.l.]:[s.n.],1997.
[10] BELLARE M,MINER S.A forward-secure digital signature scheme[C]//Proceedings of CRYPTO’99.Berlin:Springer-Verlag,1999:431-448.
[11] 王彩芬,刘军龙,贾爱库,等.具有前向安全性质的秘密共享方案[J].电子与信息学报,2006,28(9):1714-1716.
[12] 汪保友,胡运发.基于强RSA假设的签名方案[J].软件学报,2002,13(8):1729-1734.
[13] 徐文华,贺前华,李 韬.基于强RSA假设的数字签名方案[J].华中科技大学学报:自然科学版,2008,36(12):24-26.
[14] 芦殿军,张秉儒,赵海兴.基于多项式秘密共享的前向安全门限签名方案[J].通信学报,2009,30(1):45-49.
[15] 田有亮,马建峰,彭长根,等.椭圆曲线上的信息论安全的可验证秘密共享方案[J].通信学报,2011,32(12):96-102.
[16] 李慧贤,蔡皖东,裴庆祺.可验证秘密共享方案的设计与分析[J].西安电子科技大学学报:自然科学版,2008,35(1):148-151.
