基于改进的Gabor指纹纹理提取算法的研究
2018-04-13裴炜冬朱铮涛萧达安
裴炜冬,朱铮涛,杨 敏,萧达安
(1.广东工业大学 机电工程学院,广东 广州 510006;2.广东警官学院 刑事技术系,广东 广州 510440)
0 引 言
指纹识别作为近年来发展迅猛的识别技术,广泛应用于网络安全认证、社会保险、金融证券、身份验证、网络电子商务等领域,对于公安部门指纹识别尤为重要[1]。但现实生活中的指纹图像往往掺杂着各种各样的干扰,易受环境背景、光线等的影响。指纹作为个体特有的特征,虽然占全身皮肤比重极小,但指纹所包含的可识别的数据信息量极大。在犯罪现场,指纹是出现频率最高最隐蔽的特征。近年来,指纹提取的探索发展迅猛,很多科研组织对指纹提取方向的各种先进技术进行了研究,也提出了一些效果较好的处理算法,然而在复杂背景下的指纹图像的纹理提取还是有一定的难度[2-3]。
指纹纹路由相互平行的脊线和谷线组成,这些纹路会随着人们在抓取东西时而留在去体表面,指纹虽然很小却蕴含了大量的特征信息,例如三角点、分叉点、中心点纹路走向等。不同的指纹,这些特征是不相同的,公安部门可以根据这个唯一性的特征锁定犯罪嫌疑人[4]。一般的指纹图像是在背景较为多样化的环境下获取的,因此现场指纹图像里包含很多复杂的噪声和难以区分的背景。这些噪声和背景极大地影响了指纹的提取和匹配,无论是普通的滤波如Gaussian滤波、中值滤波、均值滤波,或者是Canny、Sobel、Robert、Laplace等,均不能很好地消除噪声和干扰背景。
近年来,FT、STFT、wavelet变换在信息处理与分析和图像处理方面扮演着越来越重要的角色,在信号和图像处理中获得了良好的效果,已经成为一种普遍化的信号处理分析工具。其中Gabor核函数模型的探索已经应用到信号分析、图像处理、人工智能等领域。加入了时域门限阈值函数以便去除信号无用的冗余信息而得到局部有用的可用信息,又由于窗口Fourier变换只依赖于部分时域信号,所以称这种变换为短时Fourier变换,即STFT。
1 小波变换模型
小波变换(wavelet)在图像识别、信息分析、模式识别、人工智能等领域应用广泛。由于20世纪90年代,多分辨率被引入到wavelet变换,使得wavelet的理论研究走向一个高潮,wavelet相关的理论也越来越成熟。和傅里叶变换相比,小波变换不仅能够将信号放到频域里分析,也可以同时在时域里分析,从而能从信号中提取有用信息,弥补傅里叶变换在时域的缺点。
一维小波变换为:

(1)
(2)
其中,a表示尺度参数;b表示平移参数。
二维wavelet变换指对二维图像数据在水平方向和垂直方向各自独立地进行一次一维小波变换。
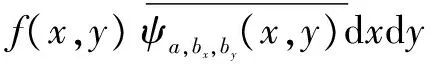
(3)
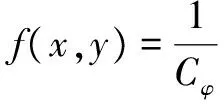
(4)
(5)

2 Gabor算法模型与文中改进的算法模型
2.1 Gabor滤波器模型
在图像处理中,Gabor核函数模型经常用于纹理的边缘描述、提取、检测。Gabor模型在频率、方向上的特点很接近于人眼视觉系统。
模型复数表达式为:
g(x,y,λ,θ,ψ,σ,γ)=
(6)
实部表达为:
g(x,y,λ,θ,ψ,σ,γ)=
(7)
虚部表达为:
g(x,y,λ,θ,ψ,σ,γ)=
(8)
(9)
以下是Gabor模型中各个参数的简要说明,包括含义和选定。
波长(λ):不同于物理学中的波长,在图像中波长通常以像素为单位,通常取值范围是3~20。
方向(θ):在Matlab中调节Gabor模型中的θ可知,θ是影响图像纹理走向的方向因子,取值范围规定在(0,2π)。
相位偏移(ψ):相对于中心的偏移量,特别地相位偏移为0和π的两个模型成中心对称。该参数的取值范围是(-π,π)。
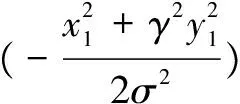
带宽(b):经理论研究证明,Gabor模型中带宽b与波长λ和a呈现一定的函数关系,其中a是Gabor模型中正态分布模型的标准差。其函数关系如下所示:
(10)
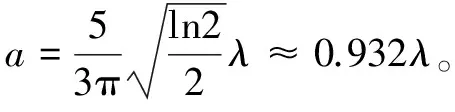
2.2 改进后的两种Gabor滤波器参数选取及添加曲率特性
Gabor核函数模型是在STFT的基础上将正交的二维正态分布函数作为门限阈值窗口函数,因此,该模型在频域和时域都能得到良好的响应。同时由于Gabor核函数模型与人眼视觉成像模型很相似,使得Gabor核函数模型具有良好的方向特性和尺度特性,在纹理提取方面具有独特的优势。尽管可以利用Gabor核函数模型的多方向特性对指纹纹理进行提取,但是一般的Gabor核函数模型不能提取指纹图像中弯曲度较大的指纹线条[5]。针对这一问题,文中提出了改进后的Gabor滤波器模型,该模型不仅在方向和尺度上具有良好的特性,而且具有很好的曲线识别能力[6-8]。改进后的两种Gabor模型式如下所述。
2.2.1 基于泰勒级数的Gabor函数模型改进
(11)
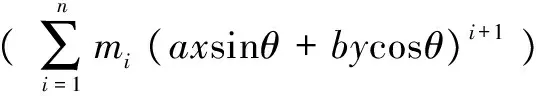

(12)
即:
(13)
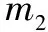
2.2.2 基于傅里叶级数的Gabor函数模型改进
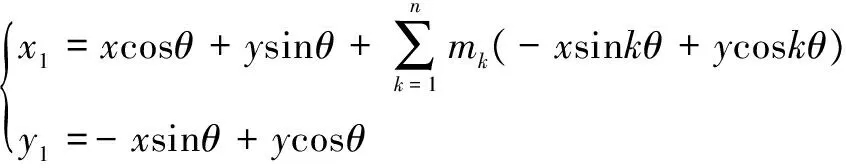
(14)
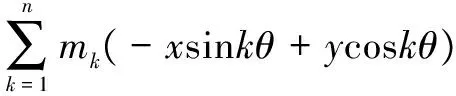
(15)
其中:
(16)
可知,对于任何符合狄利赫里约束的平滑曲线函数解析式均能用Fourier级数展开。通常取mk=1,通过调节k的值可以使改进后的Gabor滤波器能够很好地检测出指纹弯曲部分的纹线。
2.3 二维Gabor滤波的分解
图像处理用到的Gabor模型是二维离散Gabor函数,二维Gabor函数是唯一能够达到测不准原理,也就是二维Gabor模型不但可以获得很高的频域分辨率,而且还可以获得很高的时域分辨率,但在进行图像处理时运算量很大、耗时很长,这将会影响处理图像的效率。因此,提出将二维的Gabor函数分解为两个一维Gabor模型的组合[11-12]。由式(6)可以分解成:
g(x,y)=q(x)p(y)
(17)
其中:
(18)
其中,q(x)是只与x有关的x方向上的带通高斯函数;p(y)是只与y有关的y方向上的低通高斯函数[13-17]。
因此,用一个二维的Gabor核函数模型滤波可以分解为如下两个步骤,开始使用一个一维的带通高斯模型q(x)沿着图像对行方向实施卷积,然后用一个一维的低通高斯模型p(y)沿着图像对列方向实施卷积运算。
3 实验结果及分析
为检验提出算法的可靠性,对改进的Gabor核函数模型进行仿真。
不同参数的传统Gabor滤波器模型的效果图如图1所示,从第1到第5列θ取0,π/6,π/4,π/3,π/2,其他参数保持不变:ψ=0,σ=2π,γ=0.6。

图1 传统Gabor核函数
不同参数下改进后的Gabor滤波器模型的效果图如图2所示,θ取0,π/6、π/4、π/3、π/2,其他参数保持不变:ψ=0,σ=2π,γ=0.6。 改进方案1中a取-1,m和b取1,i取2;改进方案2中n取3,mk取1。

图2 改进的Gabor核函数
改进后的Gabor函数不仅具有良好的曲率特性,而且还具备良好的方向和尺度响应,通过对指纹图像的处理,发现在指纹纹脊弯曲处的局部区域的响应较强烈。
指纹纹理提取在刑侦破案中有很大的应用价值,然而由于图像的环境背景噪声及相机拍摄等问题严重影响了指纹纹理的提取与比对,也降低了条纹之间的对比度,对后续条纹的比对与识别造成了不良影响。因此提取指纹纹理是成功匹配的关键。以上结果表明,该指纹提取方法在警用指纹识别中有很好的应用价值。
4 结束语
针对基于指纹纹理识别方法,提出了两种改进的Gabor滤波器用于提取指纹的纹理,有助于后续指纹匹配度的提高。不同于传统的纹理提取算子,该Gabor滤波器模型由于具有良好的方向特性和尺度特性,因而能够对指纹纹脊弯曲部分响应明显,与其他纹理提取算子相比有更好的识别性,更加适应于图像纹理信息的提取。由于改进后的Gabor滤波器参数多、复杂,算法实时性不佳,算法的鲁棒性仍需要进一步改进。
参考文献:
[1] 张新淼.基于改进的Gabor滤波器组指纹图像识别的研究与实现[D].天津:天津师范大学,2009.
[2] 毛贤光,赖晓铮,赖声礼.改进的Gabor滤波器在指横纹提取中的应用[J].计算机工程与应用,2010,46(26):188-190.
[3] 高梓瑞.Gabor滤波器在纹理分析中的应用研究[D].武汉:武汉理工大学,2012.
[4] 毛 元,冯 桂,汤继生.采用八方向Gabor滤波的指纹识别算法[J].华侨大学学报:自然科学版,2013,34(2):151-155.
[5] 陈支泽,荆晓远,陈 芸,等.基于改进Gabor滤波器的多模态特征融合技术[J].计算机技术与发展,2015,25(10):107-110.
[6] 林克正,杨 雪.改进的基于加博滤波的指纹增强算法[J].哈尔滨理工大学学报,2009,14(4):46-49.
[7] 张玉军,徐 杨.快速Gabor滤波器在指纹纹理分析中的应用[J].鞍山科技大学学报,2006,29(3):255-258.
[8] 王 森,张伟伟,王阳生.指纹图像分割中新特征的提出及其应用[J].自动化学报,2003,29(4):622-627.
[9] JAIN A K,PRABHAKER S,HONG L,et al.Filterbank-based fingerprint matching[J].IEEE Transactions on Image Processing,2000,9(5):846-859.
[10] 贺 颖,蒲晓蓉.应用Gabor滤波的指纹识别算法的研究和实现[J].计算机工程与应用,2010,46(12):172-175.
[11] 田 捷,杨 欣.生物特征识别理论与应用[M].北京:电子工业出版社,2005:213-218.
[12] 马金辰,谢世朋,李海波.基于多个低秩纹理提取的图像校正方法[J].计算机技术与发展,2017,27(3):97-102.
[13] 韩 智,刘昌平.基于多种特征融合的指纹识别方法[J].计算机科学,2010,37(7):255-259.
[14] 戴晓薇,赵启军.基于回归的指纹方向场估计[J].计算机技术与发展,2017,27(1):1-5.
[15] 韩 智.指纹识别的应用性研究[D].北京:中科院自动化研究所,2006.
[16] AREEKUL V,WATCHAREERUETAI U,TANTARATANA S.Fast separable Gabor filter for fingerprint enhancement[J].Lecture Notes in Computer Science,2004,3072:403-409.
[17] ZHANG W P,TANG Y Y,YOU X.Fingerprint enhancement using wavelet transform combined with Gabor filter[J].International Journal of Pattern Recognition and Artificial Intelligence,2004,18(8):1391-1406.
