基于相对辨识关系的属性约简算法

2018-04-13毛建景

计算机技术与发展 2018年4期

孙滨，毛建景

(郑州工业应用技术学院信息工程学院，河南郑州 451100)

0 引言

粗糙集理论可以有效地进行不精确、不完备数据分析与处理，国外在这方面的研究已经取得了不错的成绩[1-4]，其中决策信息系统中的属性约简是其核心研究内容。许多学者利用多种方法来度量决策信息系统中属性的重要度。文献[5]在分析信息熵度量不确定性数据的基础上，定义信息熵属性重要度概念，引入蚁群优化算法，提出基于信息熵与蚁群优化的最小属性约简算法。文献[6]通过减少约简过程中基数排序次数来提升效率，设计了相对分辨能力的约简算法。文献[7]设计了一种启发式函数—决策重要度，这种启发式函数根据每个属性正决策对象集合的大小来定义其重要性，正决策对象集合越大表示重要性越高，由此构造了基于决策重要度的启发式属性约简算法。文献[8]的约简算法既考虑信息决策表的相对正域，也考虑以核属性为启发信息逐个增加条件属性时对边界域样本的影响。文献[9]定义了一种粒度差别矩阵和基于该差别矩阵的属性约简，并证明了该差别矩阵的属性约简定义与基于知识粒度的属性约简定义等价。文献[10]给出了对象矩阵的属性约简定义，证明了属性约简与基于正区域的属性约简的等价性。

因此，对于如何从海量数据集中寻找一种高效的属性约简算法，不仅能保持分类能力不变，还能简化决策规则生成过程，便具有重要的研究意义。文中依据相对辨识关系给出了基于相对辨识关系的属性约简算法，从而为属性约简提供了新的研究思路。

1 可辨识关系与属性重要度

在决策信息系统中，对于论域U，若存在属性集P、Q⊆C∪D且P、Q≠∅，使得U关于P、Q的划分相等，即U/P=U/Q，则称P、Q具有相同的可辨识能力，否则若属性集P辨识论域U中的对象对越多，则称P的可辨识能力越强，反之则辨识能力越弱。下面给出属性集的可辨识关系。

1.1 可辨识关系

为了更好地引入可辨识关系，先给出一个属性集所对应的划分的性质，方便对可辨识关系的理解。

性质1[11]：设S=(U,C∪D,V,f)为一个决策信息系统，若P⊆Q⊆C，则有U/Q⊆U/P，此时称U关于Q的划分比P更精细，U关于P的划分比Q更粗糙。

性质1仅描述了属性集对应的划分之间辨识能力的高低，并未对属性集的可辨识能力进行精确描述，因此下面给出可辨识关系的形式化定义来加以阐述。

定义1：设S=(U,C∪D,V,f)为一个决策信息系统，n为所有对象个数，对P⊆C∪D，若令

DIS(P)={|存在属性a∈P，f(xi,a)≠f(xj,a)，1≤i≤j≤n,xi,xj∈U}

则称DIS(P)为属性集P在U上的可辨识关系。

由定义1可知，DIS(P)是属性集P能辨识的所有对象对，考察的是P的辨识能力，并且可知0≤|DIS(P)|≤[|U|·(|U|-1)]/2。当U/P={{x1,x2,…,xn}}时，DIS(P)取得最小值0；当U/P={{x1},{x2},…,{xn}}时，DIS(P)取得最大值[|U|·(|U|-1)]/2。

显然U/P越精细，DIS(P)包含的对象对越多，说明利用P能辨识的对象对个数越多，越容易将论域中对象两两辨识，说明P的辨识能力越强，否则反之。

由定义1可得性质2。

性质2：设S=(U,C∪D,V,f)为一个决策信息系统，P⊆C∪D，对任意的xi、xj∈U(1≤i≤j≤n，n为论域U中对象个数)，令[xi]P、[xj]P为xi、xj所对应的P等价类，则

(1)若[xi]P∩[xj]P≠∅，则有∈DIS(P)；

(2)若[xi]P∩[xj]P=∅，则有∉DIS(P)。

由性质2可知，DIS(U,P)能辨识不同P等价类中的对象，而无法辨识同一P等价类中的对象。

由定义1可得定理1。

定理1：设S=(U,C∪D,V,f)为一个决策信息系统，P⊆Q⊆C，DIS(P)、DIS(Q)分别为P、Q的可辨识关系，则有DIS(P)⊆DIS(Q)。

证明：令任意的xi、xj∈U，其中1≤i≤j≤n。由定义1可知，若∈DIS(P)，则存在属性a∈P，f(xi,a)≠f(xj,a)，由于P⊆Q，则有a∈P⊆Q，按照定义1可知，存在属性a∈Q，f(xi,a)≠f(xj,a)，即得∈DIS(Q)。由于具有任意性，所以可得DIS(P)⊆DIS(Q)。证毕。

由定理1知，对任意集P⊆Q⊆C，则有DIS(P)⊆DIS(Q)，说明Q比P所辨识的对象对相等或更多，可辨识能力更强。特别地，当P=Q时，则有DIS(P)=DIS(Q)，此时称P、Q可辨识能力相同。

1.2 相对可辨识关系

定义2：设S=(U,C∪D,V,f)为一个决策信息系统，n为所有对象个数，对P⊆C，若令

DIS(P,D)={|存在属性a∈P，f(xi,a)≠f(xj,a)并且f(xi,D)≠f(xj,D)，1≤i≤j≤n,xi,xj∈U}

则称DIS(P)为属性集P在U上关于D的相对可辨识关系。

由定义2可知，DIS(P,D)是属性集P相对于决策属性集D能辨识的所有相对对象对，考察的是P关于D的相对辨识能力。按照定义2，可得性质3。

性质3:设S=(U,C∪D,V,f)为一个决策信息系统，DIS(P)、DIS(D)分别为P、D的可辨识关系，DIS(P,D)为P关于D的相对可辨识关系，则有DIS(P,D)=DIS(P)∩DIS(D)。

结合定义2和性质3，可得定理2。

定理2:设S=(U,C∪D,V,f)为一个决策信息系统，P⊆Q⊆C，DIS(P)、DIS(Q)、DIS(D)分别为P、Q、D的可辨识关系，DIS(P,D)、DIS(Q,D)分别为P、Q关于D的相对可辨识关系，则有DIS(P,D)⊆DIS(Q,D)。

证明：由性质3可知，DIS(P,D)=DIS(P)∩DIS(D)，又知P⊆Q，由定理1可知，DIS(P)⊆DIS(Q)。故DIS(P,D)=DIS(P)∩DIS(D)⊆DIS(Q)∩DIS(D)=DIS(Q,D)，即得DIS(P,D)⊆DIS(Q,D)。证毕。

由定理2可知，对任意集合P⊆Q⊆C，则有DIS(P,D)⊆DIS(Q,D)，说明Q比P关于D所辨识的对象对相等或更多，相对可辨识能力更强。特别地，当P=Q时，则有DIS(P,D)=DIS(Q,D)，此时称P、Q相对可辨识能力相同。

1.3 属性重要度

定义3:设S=(U,C∪D,V,f)为一个决策信息系统，P⊆C。对任意的属性a∈C-P，令

SigP(a)=(|DIS(P∪{a},D)|-

|DIS(P,D)|)/|U|2

则称SigP(a)为属性a相对于P的属性重要度。其中，|DIS(P∪{a},D)|、|DIS(P,D)|分别表示相对可辨识关系DIS(P∪{a},D)、DIS(P,D)所辨识的对象对个数，|U|为论域U的对象个数。

由于P⊆P∪{a}，由定理2可知，DIS(P,D)⊆DIS(P∪{a},D)，则存在|DIS(P∪{a},D)|≥|DIS(P,D)|，即SigP(a)≥0。显然，SigP(a)描述的是添加属性a后引起P关于D所辨识对象对的变化，SigP(a)越大，P关于D所辨识对象对越多，说明添加属性a后P的相对辨识能力提高，从而属性a对P的重要性越大。

SigP(a)度量的是在原有属性集P中添加不属于P的属性a的属性重要度，下面给出一种度量原有属性集P中每个属性a(即a∈P)的属性重要度。

定义4:设S=(U,C∪D,V,f)为一个决策信息系统，P⊆C。对任意属性a∈P，令

SigP-{a}(a)=(|DIS(P,D)|-

|DIS(P-{a},D)|)/|U|2

称SigP-{a}(a)为属性a相对于P的重要度。其中，|DIS(P,D)|、|DIS(P-{a},D)|分别为相对可辨识关系DIS(P,D)、DIS(P-{a},D)所辨识的对象对个数，|U|为论域U的对象个数，显然SigP-{a}(a)≥0。

SigP-{a}(a)描述的是在P中删除属性a后引起P关于D所辨识对象对的变化，SigP-{a}(a)越大，P关于D所辨识对象对越多，说明删除属性a后P的相对辨识能力下降，从而属性a对P的重要性越大。特别地，当SigP-{a}(a)=0时，由定义4可知，DIS(P,D)=DIS(P-{a},D)，即P、P-{a}的相对辨识能力相同，说明删除属性a后，P的相对辨识能力并未发生变化，此时称属性a为P的不必要属性或冗余属性。

结合定义4，下面给出属性a相对于P是必要属性还是不必要属性。

定义5:设S=(U,C∪D,V,f)为一个决策信息系统，P⊆C。若对任意的a∈P，都有SigP-{a}(a)>0，则每个a相对于P均是必要的，则称P为独立的，否则称P为依赖的。

1.4 约简

定义4给出了属性集P中任意属性的属性重要度SigP-{a}(a)，定义5用来判断a在P中是不必要的还是必要的，结合定义4和定义5便可给出基于相对辨识关系的属性约简方法。为了证明基于相对辨识关系的约简与文献[5]中的约简是等价的，下面先给出文献[5]中约简的定义。

定义6:设S=(U,C∪D,V,f)为一个决策信息系统，P⊆C。如果P满足：U/C=U/P；则对任意a∈P，U/C≠U/(P-{a})，则称P是C的一个约简。

由定义4、5、6，给出基于相对辨识关系的约简的判定方法，可得定理3。

定理3:设S=(U,C∪D,V,f)为一个决策信息系统，P⊆C。若P是独立的且DIS(P,D)=DIS(C,D)，则称P为C的一个约简。

证明：若P是独立的且DIS(P,D)=DIS(C,D)，因P⊆C，由定理1得DIS(P)⊆DIS(C)，若U/P≠U/C，则DIS(P)⊂DIS(C)，DIS(P)∩DIS(D)⊂DIS(C)∩DIS(D)，由定理2可知，DIS(P,D)⊂DIS(C,D)与条件DIS(P,D)=DIS(C,D)矛盾，所以U/P=U/C，P满足定义6第一个条件。

又因为P是独立的，则对任意的a∈P，都有SigP-{a}(a)=(|DIS(P,D)|-|DIS(P-{a},D)|) / |U|>0，则知|DIS(P,D)|>|DIS(P-{a},D)|，即DIS(P-{a},D)⊂DIS(P,D)，故U/P-{a}≠U/P，所以U/P-{a}≠U/C，P满足定义6第二个条件，可知P是C的一个约简。

由定理3可知，文中约简与文献[5]中约简等价。

2 基于相对辨识关系的属性约简算法

2.1 算法思想

基于相对辨识关系的属性约简算法思想是首先令约简集Red(S)=∅，对任意属性a∈C，按照定义3依次计算各条件属性关于D的相对可辨识关系DIS({a},D)，选择对象对个数最大的属性加入约简集Red(S)中。然后，判断当前约简集Red(S)关于D的可辨识关系是否等于DIS(C,D)，若是则输出Red(S),即为该决策信息系统的约简;否则，对任意属性a∈C-Red(S)，按照定义3依次计算属性重要度SigRed(S)(a)，选择对象对个数最大的属性加入约简集Red(S)中，再次判断是否满足定理3关于约简的要求，不断重复这个过程，最终输出满足要求的Red(S)，即为该决策信息系统的约简。

由此可知，该算法是从条件属性集中先判断各个属性的相对可辨识关系，其对象对个数最大者组成约简集，然后再在此约简集中逐渐添加属性，直至满足约简条件，是一种无核的属性约简算法，无论算法时间复杂度还是约简工作量在一定程度上都有所降低。

2.2 算法实现

定理3利用相对辨识关系约定了约简满足的要求，下面给出一种基于相对辨识度的属性约简算法—RDR算法(an attribute reduction algorithm based on relative discernible relation)。

输入：一个决策信息系统S=(U,C∪D,V,f)，其中U={x1,x2,…,xn}，C={a1,a2,…,am}；

输出：决策信息系统的约简Red(S)。

步骤1：令Red(S)=∅，按定义2计算相对可辨识关系DIS(C,D)；

步骤2：令Red(S)={a}，其中|DIS({a},D)|=max{|DIS({ai},D)|ai∈C,i=1,2,…,m}(如果多个属性均满足，则任选一个加入Red(S))且|DIS({ai},D)|≠0；

步骤3：若DIS(Red(S),D)=DIS(C,D)，则算法终止，输出Red(S)(此时的Red(S)为S的一个约简)，否则执行步骤4；

步骤4：令Red(S)=Red(S)∪{b}，并且SigRed(S)(b)=max{SigRed(S)(b')|bi∈C-Red(S),i=1,2,…,m}(如果多个属性满足，任选一个加入Red(S))，转步骤3。

2.3 实例验证

下面是采用文献[12]中的决策信息系统(见表1)，其中文献[12]得到的约简是{a1,a3}。

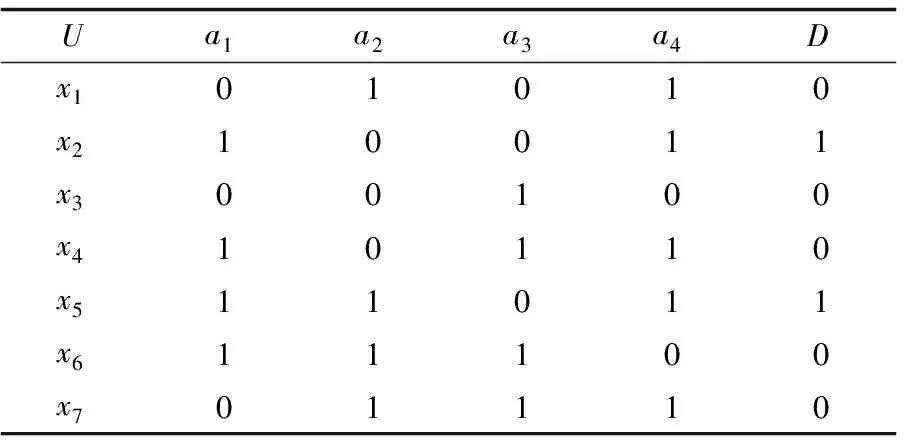
表1 决策信息系统S

首先，令Red(S)=∅，DIS(C,D)={,,,,,,,,,}。

对于任意的a∈C，逐一计算其可辨识关系DIS({a},D)：

DIS({a1},D)={,,,,,}DIS({a2},D)={,,,,}

DIS({a3},D)={,,,,,}

DIS({a4},D)={,,,}

则可知，|DIS({a1},D)|=|DIS({a3},D)|>|DIS({a2},D)||DIS({a4},D)|，按照步骤2，在属性a1、a3中任意一个属性加入Red(S)(此处选择a1)，即此时Red(S)={a1}。

按照步骤3，判断式子DIS(Red(S),D)=DIS(C,D)是否成立。显然，由上述所求相对辨识关系，可得DIS(Red(S),D)=DIS({a1},D)≠DIS(C,D)，执行步骤4。

先计算所有属性集Red(S)∪{b}(b∈C-Red(S))关于D的相对辨识关系。

DIS({a1,a2},D)={,,,,,,,}DIS({a1,a3},D)={,,,,,,,,,}DIS ({a1,a4},D)={,,,,,,}

按照定义3，对于所有属性b∈C-Red(S)，计算其重要度SigRed(S)(b)。

Sig{a1}(a2)=(|DIS({a1,a2},D)|-|DIS({a1},D)|)/|U|=(8-6)/14=1/7，Sig{a1}(a3)=(|DIS({a1,a3},D)|-|DIS({a1},D)|)/|U|=(10-6)/14=2/7，Sig{a1}(a4)=(|DIS({a1,a4},D)|-|DIS({a1},D)|)/|U|=(7-6)/14=1/14。显然，Sig{a1}(a3)值最大。按照算法步骤4，将属性a3加入当前Red(S)中，此时Red(S)={a1,a3}。

按照步骤3，判断式子DIS(Red(S),D)=DIS(C,D)是否成立。显然，由上述所求相对辨识关系，可得DIS(Red(S),D)=DIS({a1,a3},D)=DIS(C,D)，算法终止，输出当前Red(S)={a1,a3}，即{a1,a3}为该决策信息系统的约简，这与文献[12]所得到的结果一致，说明该算法是有效的。

2.4 算法比较

本节给出该算法复杂度分析，并与其他算法进行对比。

(1)对于步骤1，计算DIS(C,D)的时间复杂度为O(|C||D|)；

(2)对于步骤2，要计算所有a∈C中的所有可辨识关系集合对象个数，所以该步的时间复杂度为|C|×O(|C||U|)；

(3)对于步骤3，需要判断DIS(Red(S),D)=DIS(C,D)的时间复杂度为O(|Red(S)||U|) (Red(S)⊆C)；

(4)对于步骤4，计算SigRed(S)(b)的时间复杂度为O(|C|2|U|)。

综上可以得出，文中的RDR算法时间复杂度为O(|C||U|)+|C|×O(|C||U|)+O(|Red(S)| |U|)+O(|C|2|U|)=O(|C|2|U|)。

文献[13]算法的时间复杂度为O(|C|2|U|2)，文献[12]算法的时间复杂度为O(|U||A|2|A|log|U|)，相比之下RDR算法至少也为O(|C|2|U|)，因此要优于文献[12-13]算法。又因为该算法是往约简集中逐渐添加属性，不需要重复计算条件属性集的核集，大大减少了计算量，一定程度上降低了复杂度，提高了算法效率。