高斯脉冲光场下的三阶非线性极化率的研究

任静波，朱长军

（西安工程大学 理学院，陕西 西安 710048）

0 引言

非线性光学的发展经历了几个阶段：20世纪60年代主要进行了二次谐波产生、和频、差频、双光子吸收、受激喇曼散射、受激布里渊散射、光参量振荡、自聚焦、光子回波、自感应透明等非线性光学现象的观察和研究；20世纪70年代人们更深入地研究了上述现象，并进行了自旋反转受激喇曼散射、光学悬浮、消多普勒加宽、双光子吸收光谱技术、相干反斯托克斯喇曼光谱学、非线性光学相位共轭技术、光学双稳效应等非线性光学现象的研究；20世纪80年代，倍受人们注意的非线性光学新研究课题是光学分叉和混沌、光的压缩态、多光子原子电离现象等。目前，非线性光学已逐渐由基础研究阶段进入应用基础研究和应用研究阶段[1-3]。

牛海军等人[4]设计合成并表征了新颖的具有三阶非线性光学性能的含有富电子结构单元的共轭聚希夫碱，用Z-扫描技术研究了目标产物的三阶非线性特性，测定了目标产物吡咯烷酮溶液的三阶非线性折射率及非线性吸收率。严祥安等人[5]在∧型三能级原子系统中，利用Stark啁啾快速绝热通道技术控制基态和激发态之间的粒子布居转移，采用耦合波方程和哈密顿方法得到了三阶极化率与非线性转换系数的关系。吴文智等人[6]利用超短脉冲Z扫描技术和光学Kerr效应研究了以巯基丙酸为稳定剂的CdTe量子点水溶液的三阶光学非线性极化特性。在532 nm，3 0 ps和800 nm，130 fs脉冲激光激发下，发现分别具有正负相反取值的三阶光学非线性折射率，自由载流子吸收和双光子吸收分别是这两种脉冲激光激发下三阶光学非线性吸收的起因。郑勇林等人[7]应用有效非线性电导理论，讨论了随机分布的复合磁性颗粒材料的非线性行为，得到金属颗粒复合体系的有效非线性电导率与平方电导的关系式，在此基础上，导出了小颗粒在无涡流情况下系统的有效光学非线性极化率的表示式。金朝辉等人[8]采用飞秒共振简并四波混频技术，检测了花菁染料的聚乙烯醇延伸膜平行和垂直于延伸方向的三阶非线性光学极化率。Wang Guanghui等人[9]研究了一个特殊非对称量子阱中的二阶非线性光学极化率，并且利用量子力学中的密度矩阵算符理论和迭代方法导出了二次谐波极化率的解析表达式。并以典型的GaAs/AlGaAs非对称量子阱为例作了数值计算。郑涛等人[10]提出了将简并四波混频激光光谱分析技术用于物质超精细结构检测，使用量子光学理论计算的新方法测量同位素含量。即由实验现象确定出自激振荡频率后，在三阶极化率的基础上。通过量子光学梯形三能级系统的计算，得到了简并四波混频双光子共振吸收下，三阶极化率与原子数密度的关系。张彦鹏等人[11]从理论上系统地研究了由于五阶极化强度间的干涉所导致的级联三能级系统相位共轭超快调制光谱学。武海斌等人[12]在理论上研究了A型三能级原子系统Raman跃迁中的线性和非线性极化率。

1 原子三能级系统三阶非线性极化率的迭代法

对于三能级原子系统，如图1所示，下能级|a＞是基态能级，上能级|b＞和|c＞是激发态能级。

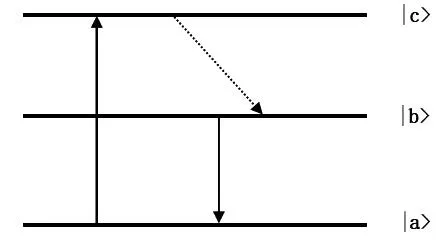
图1 三能级系统示意图

a，b，c，其密度矩阵为

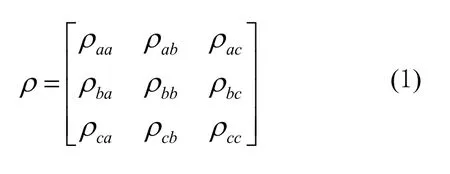
对角矩阵元表示原子处于某个态的概率，非对角矩阵元表示原子在不同态之间跃迁的概率。在初始条件已知的情况下，求出原子在不同态之间跃迁的概率，即非对角密度矩阵元，就能够得到原子处于某个态的概率，即对角密度矩阵元。因此，我们只讨论非对角密度矩阵元。

密度矩阵元的运动方程为[13]

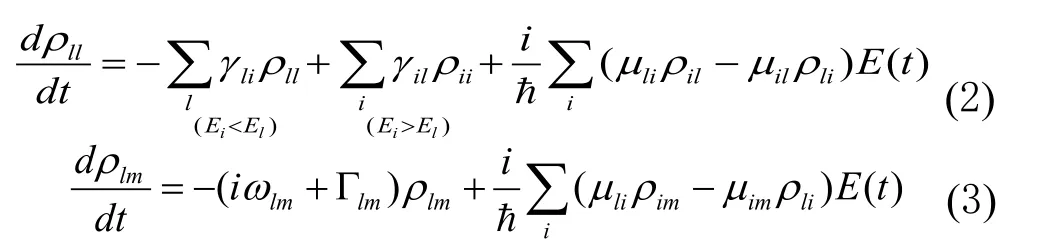
将密度矩阵元作微扰展开

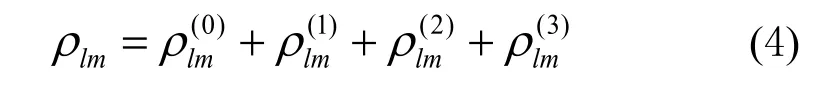
我们在此讨论级联过程。级联过程是指原子系统跃迁过程为a→b→c，即与级联单光子跃迁相联系。因此，级联过程中，高阶矩阵元仅仅由与其相邻的低阶矩阵元生成。我们采用迭代法求解各阶非对角密度矩阵元。在迭代法中，高阶矩阵元是由低阶矩阵元与光场的作用而生成。

1.1 一阶非对角密度矩阵元

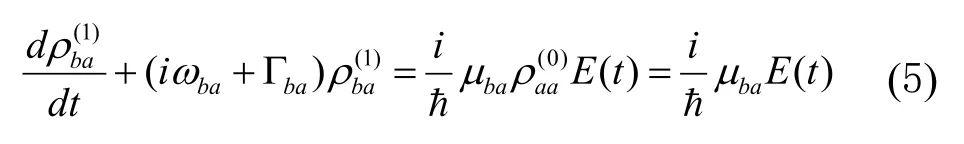
通解为

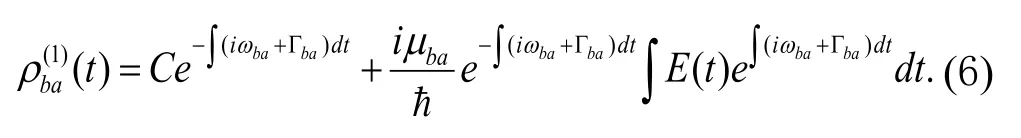
对于单光子激发过程，有

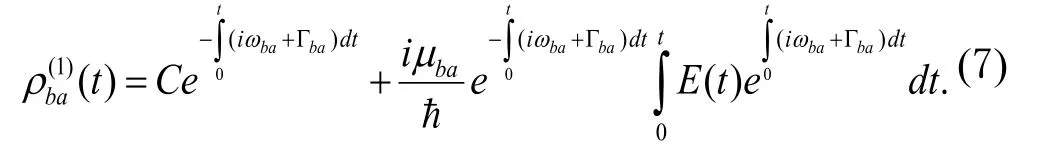
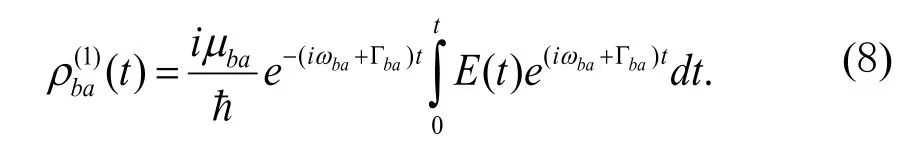
其它一阶非对角密度矩阵元均为零。

1.2 求解二阶非对角密度矩阵元

把公式(8)代入(3)，得到

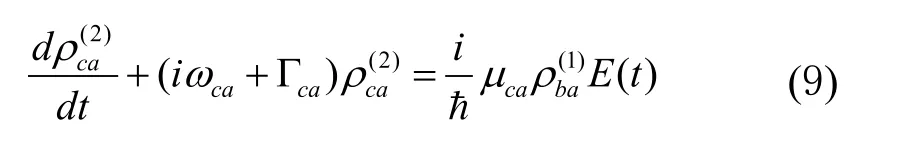
那么二阶非对角密度矩阵元为

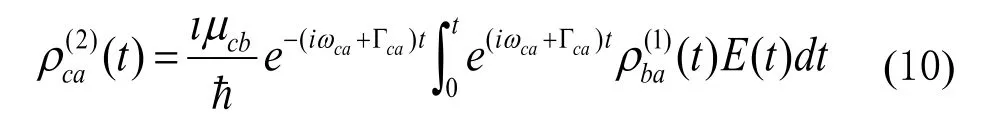
其它二阶非对角密度矩阵元均为零。

1.3 三阶情况，求解三阶非对角密度矩阵元

把公式（10)代入(3)，采用相同的步骤得到三阶非对角密度矩阵元

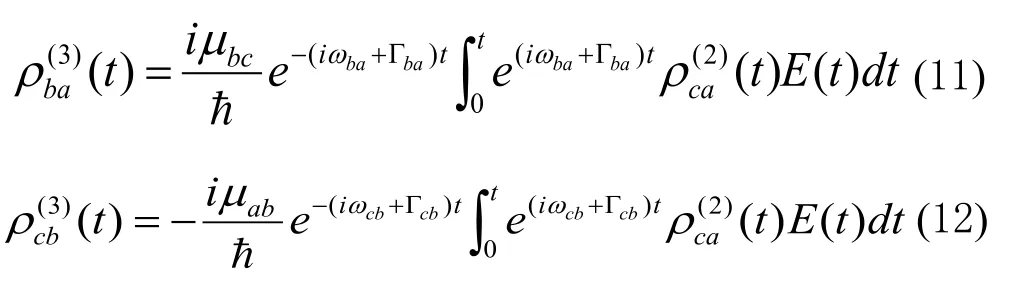
其它三阶非对角密度矩阵元均为零。

由公式(11)和(12)可知，当仅仅考虑级联过程时，c和a之间无法产生直接一步跃迁，所以。表明级联过程仅仅适用于光场的频谱宽度较窄的情形。

因此，原子三能级系统级联过程的三阶非线性极化率可由三阶微扰密度矩阵元表示

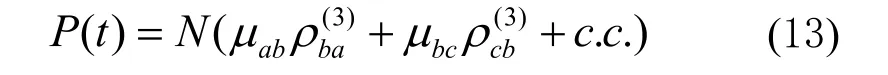
其中N是原子数密度。

2 光场为单色波的三阶非线性极化率

在光场为单色波的情况下，只能实现级联过程。设单色波光场的表达式为

2.1 单色波光场作用下一阶非对角密度矩阵元

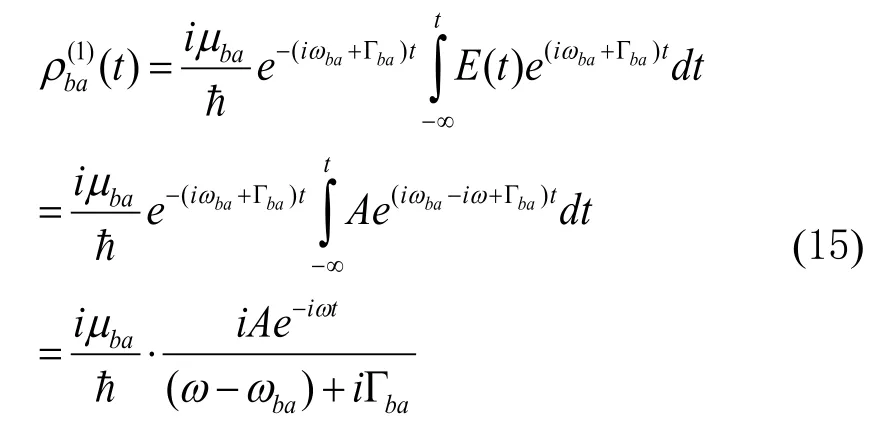
其它一阶非对角密度矩阵元均为零。

2.2 单色波光场作用下二阶非对角密度矩阵元

把（15）代入(10)，得到二阶非对角密度矩阵元

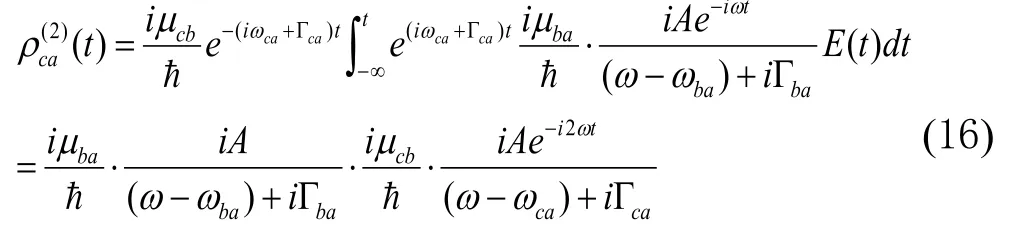
其它二阶非对角密度矩阵元均为零。

2.3 单色波光场作用下三阶非对角密度矩阵元

把（16）代入(11)，得到三阶非对角密度矩阵元

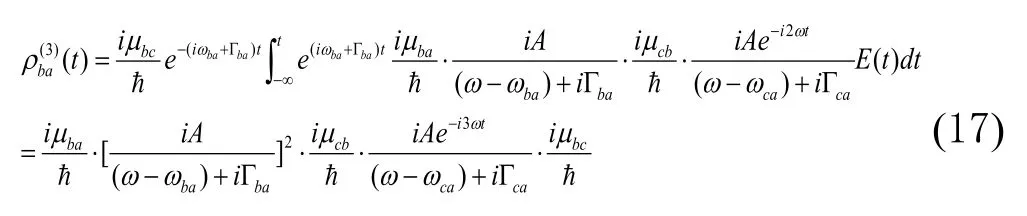
把（16）代入(12)，得到三阶非对角密度矩阵元

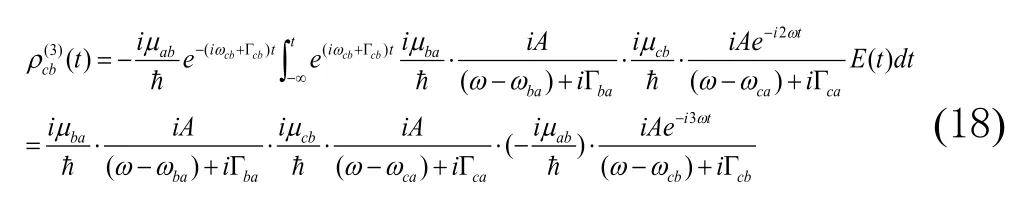
从（17）、（18）式可知，其中出现了二倍于光场频率的新频率。从三阶非对角密度矩阵元的表达式可知，其中出现了三倍于光场频率的新频率。三阶极化率与光场振幅的三次方成正比。当光场频率与能级之间能量差相等时，出现共振，此时，三阶非线性极化率急剧增大。

3 光场为高斯脉冲的三阶非线性极化率

在光场为高斯脉冲的情况下，当高斯脉冲的频谱宽度远远小于能级之间能量差时，会出现级联过程。设高斯脉冲光场的表达式为

3.1 求解高斯光场作用下一阶非对角密度矩阵元

首先考虑级联过程的一阶情况，求解高斯光场作用下一阶非对角密度矩阵元。把公式(19)代入公式(8)中，得到一阶非对角密度矩阵元为

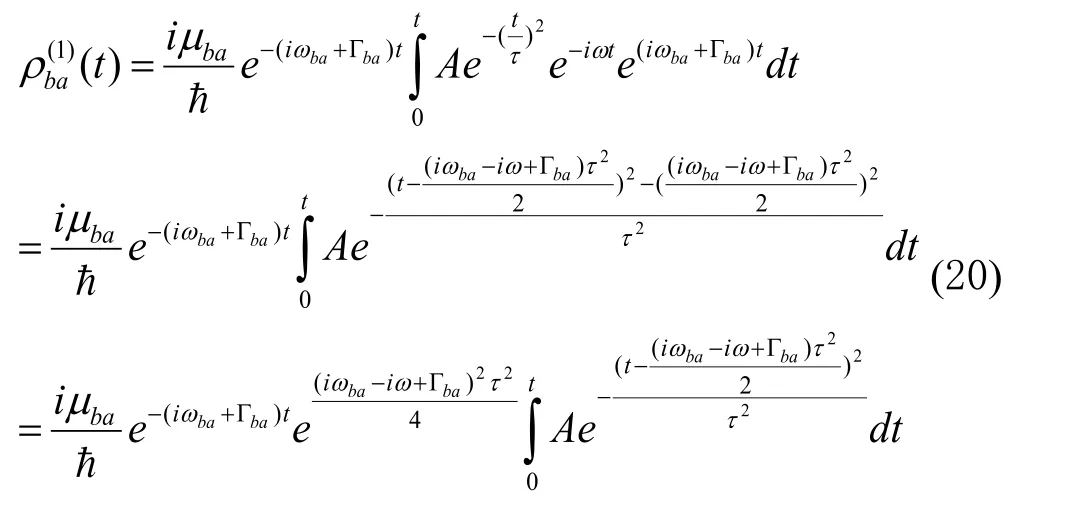
忽略t到∞时间段的贡献。于是，(20)式中积分的上、下限分别近似为∞和0，因此(20)式可变为

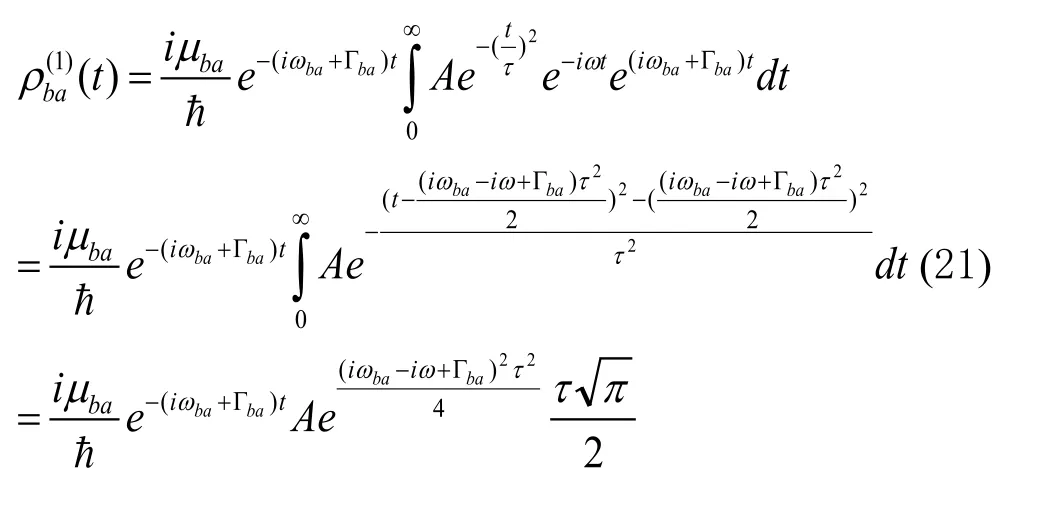
3.2 求解高斯光场作用下二阶非对角密度矩阵元

其次考虑二阶情况，求解高斯光场作用下二阶非对角密度矩阵元。同理，把公式(21)代入公式(10)中，得到二阶非对角密度矩阵元为

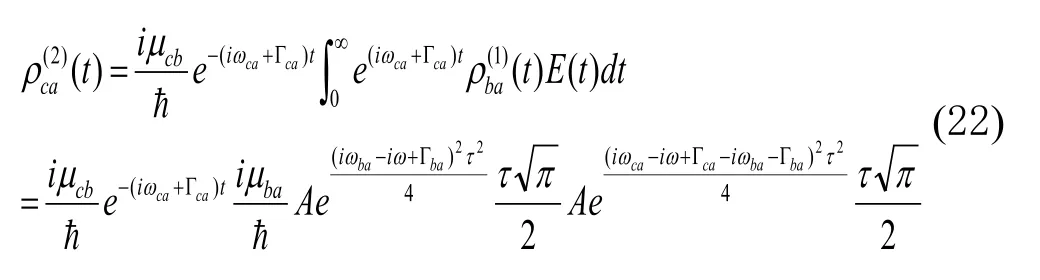
3.3 求解高斯光场作用下三阶非对角密度矩阵元

最后考虑三阶情况，求解高斯光场作用下三阶非对角密度矩阵元。把公式(22)分别代入公式(11)、(12)中，得到三阶非对角密度矩阵元：

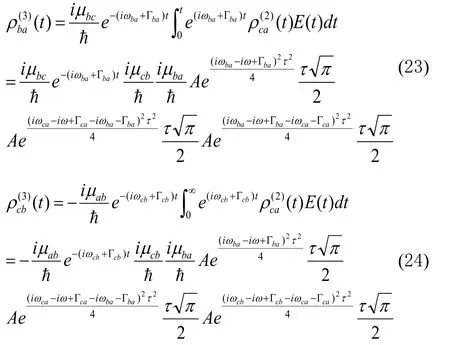
从（23）、（24）可知，在非级联过程中，其三阶极化率与光场振幅的三次方成正比，且随脉冲宽度平方的增加而指数增加。而且三个能级同时激发，三阶极化率包含了三个频率，且分别以衰减常数按指数衰减。

4 结论

在光场为单色波的情况下，从二阶非对角密度矩阵元的表达式可知，其中出现了二倍于光场频率的新频率。在三阶非对角密度矩阵元的表达式中出现了三倍于光场频率的新频率，而且三阶极化率与光场振幅的三次方成正比。高斯光场情况下，分别讨论级联过程和非级联过程，两种过程有显著的区别，在非级联过程中，其三阶极化率与光场振幅的三次方成正比，且随脉冲宽度平方的增加而指数增加。而且三个能级同时激发，三阶极化率包含了三个频率，且分别以衰减常数按指数衰减。当光场频率满足下列共振条件时三阶极化率按指数急剧增加。