单稳和双稳机制中的光力纠缠

2018-04-12严冬张孟龙王彬彬

长春大学学报 2018年10期

严冬，张孟龙，王彬彬

(长春大学理学院，长春130022)

纳米时代的到来促使量子光力学研究进一步繁荣发展。纳米技术的快速进步使得微小质量和高品质机械振子的制造成为可能，而这类机械振子通常可以作为感应微弱光辐射压力(通常忽略不计)的光力学装置[1-2]。一方面，能够利用各种光力学系统有效地探索新奇量子行为[3];另一方面，由于其固有的经典和量子二重特性，量子光力学为实现超精密测量铺平了道路[4-6]。伴随着研究的不断深入，人们发现，量子光力学系统具有极强的扩展性，甚至能够耦合其他物理系统不易兼容的自由度，构造出新型的混合量子相干器件，实现更为丰富的物理功能[2]，例如与原子系综混合实现电磁感应透明型机械透明的相干控制[7-8]。

此外，量子纠缠作为量子信息处理和量子物理的核心资源，在理论和应用上有着极其重要的地位。研究表明，在光力学系统也存在着类似的量子关联-光力纠缠[9-10]，即腔内的量子光场与宏观的机械装置产生纠缠，这样不但可以利用光力学手段作为有力的工具探究量子物理的实质，还能够为量子信息技术提供全新的量子界面。

本文研究具有单、双稳特征的光力纠缠。系统地考察和判断模型的稳定条件，进一步利用刻画连续变量纠缠的手段准确而有效的评估单稳与双稳机制下光力学纠缠特性并给出物理解释。

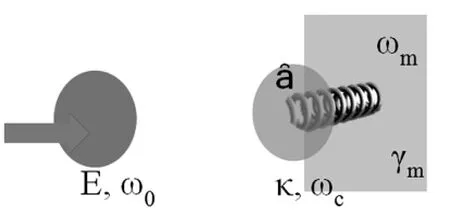
图1 典型的光力学系统

1 光力学系统的动力学方程以及纠缠量度

如图1所示的典型光力学系统:法布里-珀罗微腔一端为固定的半反半透腔镜，另一端为全反射的可移动腔镜。频率为ω0的经典光场E通过固定腔镜端入射并激发腔内的单模光场a，频率为ωc。该单模腔场推动频率为ωm的可移动腔镜产生微小位移。该系统的哈密顿为:

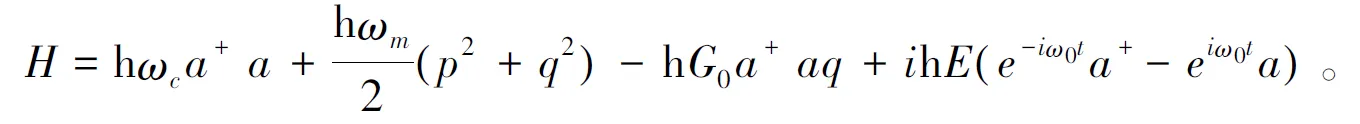
(1)

其中，第一项为单模腔场的自由哈密顿，a+、a分别为产生和湮灭算符，满足对易关系[a，a+]=1;第二项为可以移动腔镜的自由哈密顿，p、q分别为可移动腔镜的无量纲动量和位移，满足对易关系[q，p]=i。第三项是光力相互作用哈密顿，为耦合强度，L为处于腔镜平衡位置时的长度。最后一项为腔内腔外相互作用哈密顿，，P为功率，κ为腔镜弛豫速率。

计及腔内光子损耗和量子噪声，系统的动力学可以用郎之万方程来描述:

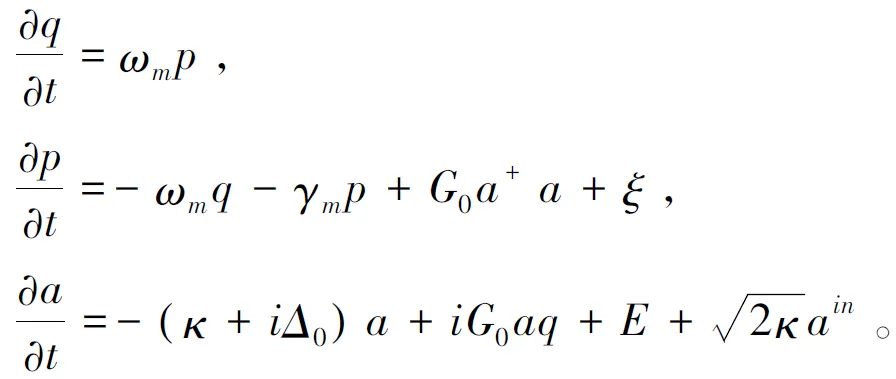
(2)

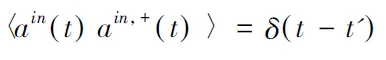
考虑到研究系统的关联，需要对算符进行线性化，即a=αs+δa，q=qs+δq以及p=ps+δp。将线性化的方程代入郎之万方程，会得到稳态解，这里有效失谐Δ=Δ0-G20αs/ωm。同时得到涨落满足的方程:

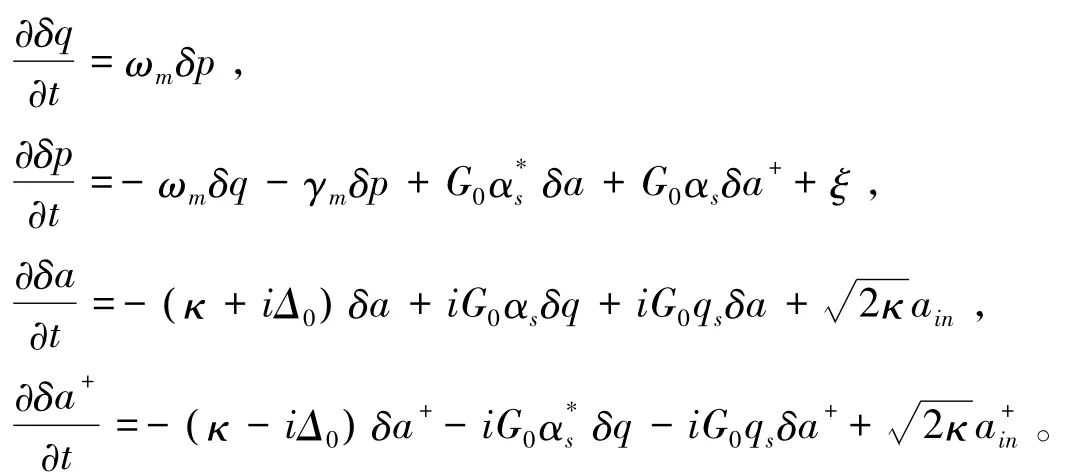
(3)

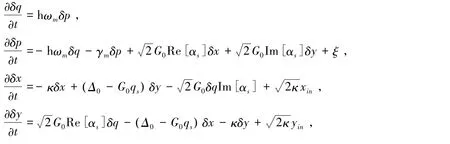
(4)

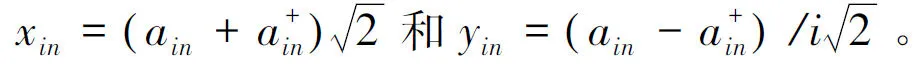
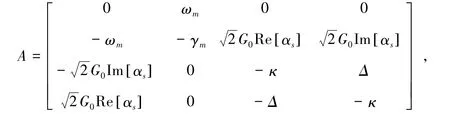
(5)

如果仅仅考虑αs是实数，即，则可以退化为:

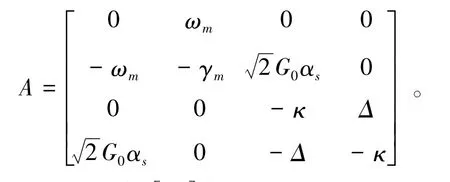
(6)

这时与文献[10]完全一致。

根据Routh-Hurwitz判据，系数矩阵A的本征值具有负实部，方程(4)才稳定，基于此可以得到以下两个非平凡的判据，即:

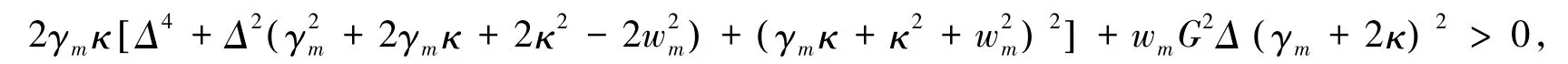
(7)

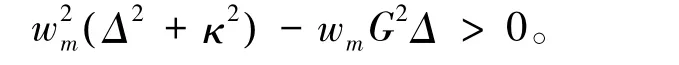
(8)

当系统的稳定条件得到满足，可以计算稳态关联矩阵V满足的方程:

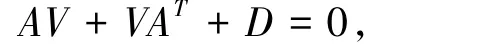
(9)

这里有:

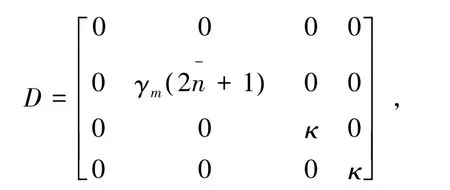
(10)

在此基础上可以用En量度光力学纠缠。在连续变量系统中，有:

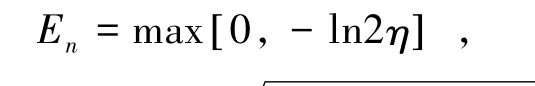
(11)

(12)

是4×4的方阵，而A，B，C为2×2的块方阵。

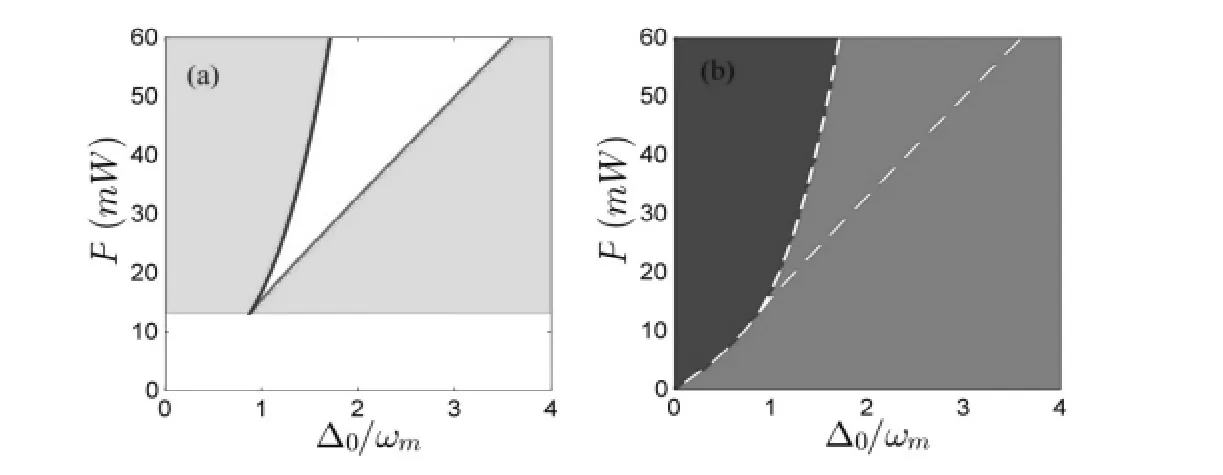
图2 (a)腔内光子强度Is解分布示意图，(b)系统光力学单、双稳相图

2 数值结果讨论与分析

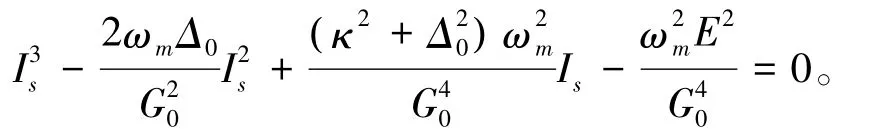
(13)

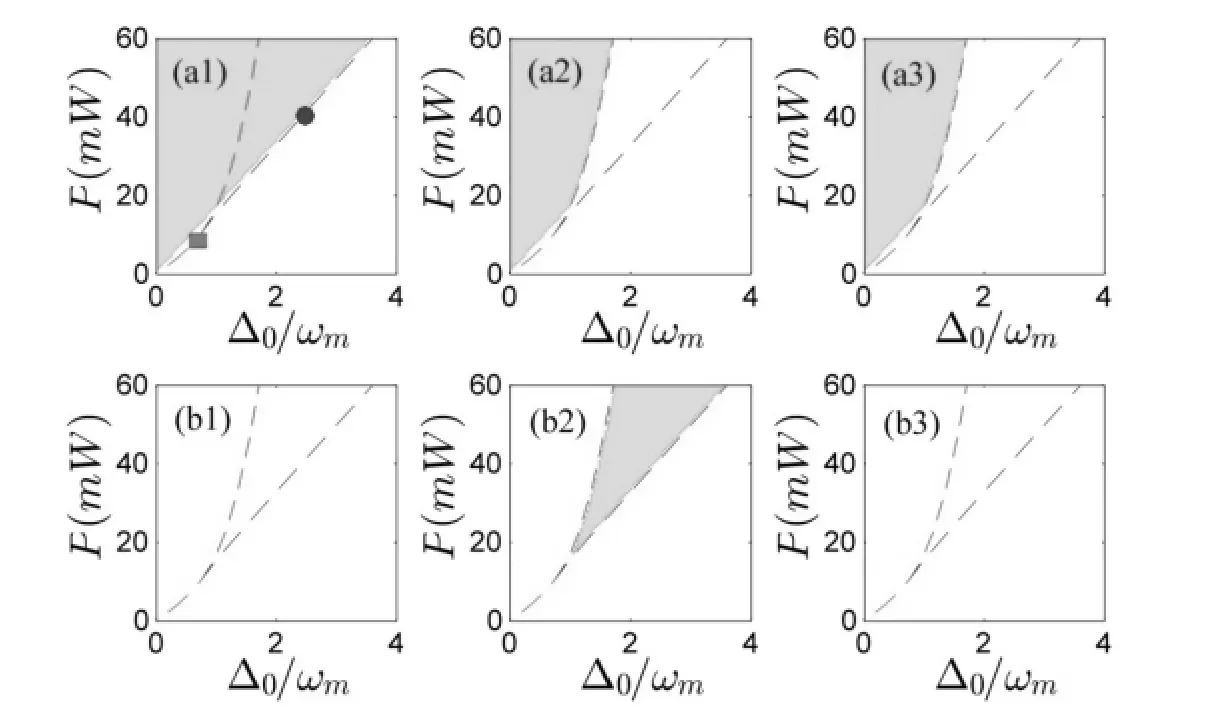
图3 涨落稳定性相图。第一、二行分别利用判据一、二来计算。第一、三列来自双稳的两个解，中间一列为不稳定的第三个解。绿色为不满足判据的参数空间。

在此基础上，进一步利用Routh-Hurwitz判据来判断系统涨落满足的稳定条件。当且仅当方程(13)的解同时满足两个判据时，系统涨落的演化才会趋于稳定。图3表明:双稳机制下，双稳解中一个无条件满足，另一个处处不满足，而第三个不稳定的解完全不满足;而单稳机制下，只有当P＜ωcωm[Δ0(Δ20+9κ2)-(Δ20-3κ2)3/2]/27κG20时才不违背Routh-Hurwitz判据。只有满足Routh-Hurwitz判据才可以进一步计算纠缠。

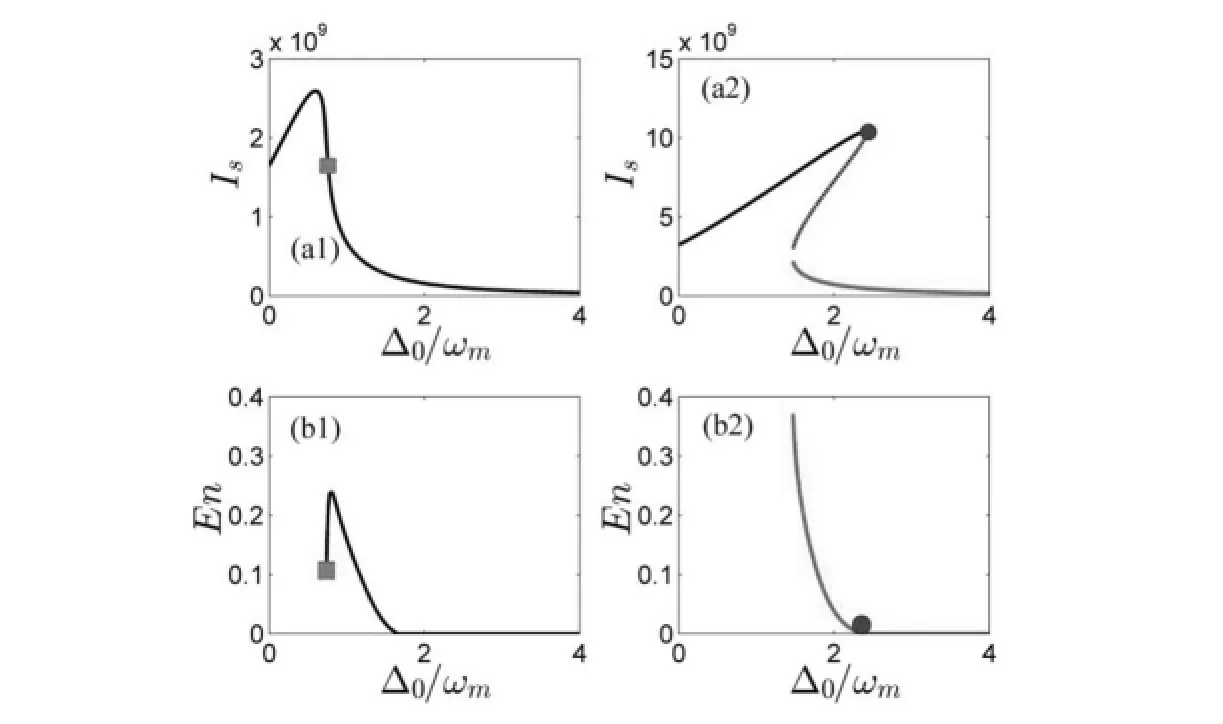
图4 单稳和双稳机制下腔内光子强度和光力纠缠。左右两列分别对应功率10mW和40mW，红、蓝标记与图3一致。

现在考察单、双稳机制下的光力纠缠。从图4可知，无论是单稳还是双稳机制，纠缠最大值与腔内最大光子强度并不对应。也即腔内光子数最多时，尽管可以推动腔镜达到最大位移，但是并不意味着量子纠缠最大。反而是当腔内光子数目急速下降或者上升时候，量子纠缠最大。对于单稳情况，这两种情况都存在，是可逆的。而双稳情况，由于系统的连续性被破坏，所以不存在可逆。只有光子数目即将急剧增多时候，也就是在下支到上支转换的边界处量子纠缠最大。