求解作业车间调度问题的变邻域动态烟花算法
2018-04-11钱晓雯
钱 晓 雯
(苏州卫生职业技术学院 基础部,江苏 苏州 215006; 苏州大学 计算机科学与技术学院,江苏 苏州 215006)
0 引 言
作业车间调度问题(Job-Shop Scheduling Problem, JSP)具有不确定性、复杂性、多约束条件以及多资源相互协调等特点[1],一直是机械加工制造、网络通信、集成电路设计等诸多研究领域的数学难题[2]。如何在满足多种约束条件的前提下,达到所需性能指标最优,具有重要的理论意义和实际价值。
国内外学者针对JSP问题的求解提出了许多行之有效的方法[3]。这些方法大致可分为精确计算、构造式启发算法和智能优化算法。其中,智能优化算法作为一种具有全局优化性能、通用性强、且适合解决大规模问题的并行算法[4],近年来已成为解决JSP问题最为常见的方法。Heinonen等[5]提出采用蚁群算法和后处理阶段的混合算法求解最小化完成时间的JSP问题,但是该算法容易陷入局部最优,且计算复杂性较大。Chen等[6]提出利用基于改进的遗传算法求解JSP问题,该算法在遗传算法的基础之上改进变异操作,引入交叉点数量的判断条件,能在一定程度上提高算法性能,但是改进后的算法复杂难以理解,且计算时间开销较大。杨小东等[7]提出一种结合帝国主义竞争算法和禁忌搜索算法的混合算法用于求解最小化最大完成时间的JSP问题,该算法能较好地兼顾全局最优与局部最优,但是算法收敛速度慢。姚远远等[8]提出布谷鸟算法求解JSP问题,但是该算法有效性不高,且鲁棒性较差。烟花算法(Fireworks Algorithm, FWA)[9]作为智能优化算法家族新成员,一经提出便因其结构简单、性能优越而受到广泛关注[10-12]。但是,FWA并未考虑不同个体之间的相互联系,使得算法容易陷入局部最优。
本文提出一种基于变邻域搜索的动态烟花算法(Dynamic Fireworks Algorithm base on Variable Neighborhood Search, DFWA-VNS),并用于求解JSP问题。DFWA-VNS在FWA的基础之上,引入变邻域搜索方法,在多种邻域结构下按贡献选择不同的搜索方式,同时,对每次进化中,根据算法进化速度动态确定每次更新维数,以此提高JSP问题求解精度,并避免算法陷入早熟问题。
1 JSP的数学模型
JSD可描述为:给定m台机器,n个作业,每个作业按指定的顺序在m台机器上依次进行,但必须满足约束条件:① 预先设置每个工序的加工时间和加工机器;② 每个工序有且只能在1台机器上加工1次;③ 不同作业之间无前后约束关系;④ 每道工序不能中断;⑤ 每台机器不能同时加工多个作业;⑥ 完工时间只考虑加工所需时间,不考虑开始前的布置时间和工序间的交接时间。
综上,可将JSP问题转换成数学模型。设工件j在机器k上的执行时间为pj,k,工件j的第i个操作在机器k上的执行完成时间为t(ji,k),所有工件的排序为r(j1,j2,…,jn),R为所有排序的集合。由于同一机器不能同时加工多个工件,所以机器k必须在执行完操作ji-1之后才能进行操作ji,与此同时,操作ji必须完成上一机器k-1的操作,数学表达式为:
(1)
i=2,3,…,n;k=2,3,…,m
则所有工件的最大完工时间为:
tmax(r)=t(jn,m)
(2)
因此,最小化最大完工时间即为:
minf=min[tmax(r)]∀r∈R
(3)
2 烟花算法
在FWA中,每个烟花均视为一个可行解,烟花爆炸产生火花的过程被视为其邻域搜索过程,但是,每个烟花的爆炸半径和爆炸产生的火花数均不同。适应度值差的烟花爆炸半径较大,具有全局搜索能力;反之,适应值好的烟花爆炸半径较小,具有局部搜索能力。在整个搜索过程中,烟花之间通过资源分配和信息交互推动算法寻优过程,最终得到最优解。
3 DFWA-VNS算法
3.1 变邻域搜索
变邻域搜索[13](Variable Neighborhood Search, VNS)是一种重要的元启发式搜索算法,已广泛应用于多个领域。VNS通过搜索状态在给定的邻域结构集合中系统地变化邻域结构来拓展搜索范围,从而提高算法的全局寻优能力。本文引入3种领域结构:① 交换。随机交换工序执行顺序中的两个不同工件的位置。② 插入。将随机选择的某一工件插入到工序中的一个随机位置。③ 逆序。随机选择一段序列间的工件,并将工件逆序。通过该3种方式改变邻域结构,可有效避免JSP问题求解过程中陷入局部最优困境。
3.2 DFWA-VNS算法
3.2.1动态烟花算法
每个烟花爆炸以后产生的火花总数为:
(4)
式中:i(i=1,2,…,n)表示烟花序号;ymax表示所有烟花对应的目标函数的最大值,ymax=max(f(xi))(i=1,2,…,n);ξ表示一个极小量,防止式中出现除零错误;l表示所有烟花爆炸产生的火花总数。
烟花i(i=1,2,…,n)的爆炸半径为:
(5)
式中:ymin表示所有烟花对应的目标函数的最小值,且ymin=min(f(xi))(i=1,2,…,n);Amax表示最大爆炸半径。
在进化过程中,多样性是保证算法搜索范围达到全局最优的重要性能。为避免算法性能优秀的个体对子代影响过大,导致种群多样性减弱甚至丧失,需对烟花总数si进行约束:
(6)
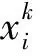

(7)

(8)
通过式(7)或式(8)产生新的位置如果超出了搜索范围,则需要采用映射规则使其返回搜索空间内。映射规则如下式:
(9)

但是,在进行位置更新时,需要更新的维度z难以确定。如果z过大,将使得群体多样性减弱,容易陷入局部最优;反之,如果z过小,将减慢优化速度,较低算法收敛能力。因此,本文引入动态更新策略。
定义烟花种群的进化速度为v,在第t次迭代计算时,将前t-1次迭代计算中的最优值进行线性拟合,得到拟合函数:

(10)

通过进化速度v进而确定需更新维度z的大小
(11)
式中:μ,λ∈(0,1)为调整因子;v0为速度阈值,需初始时刻设定。通过z的动态调整,加快算法收敛速度,同时增强全局寻优能力。
3.2.2DFWA-VNS算法步骤
(1) 初始化相关参数,生产n个初始烟花。
(2)n个烟花发生爆炸,计算每个烟花的爆炸半径和火花个数。
(3) 根据爆炸半径和火花个数生产爆炸火花和高斯变异火花。
(4) 计算进化速度并根据进化速度动态调整更新维度z。
(5) 根据邻域变化规则调整搜索邻域。
(6) 选择下一次迭代计算的父代烟花。
(7) 判断是否满足终止条件。若满足则输出最优值,并停止计算;否则返回第(2)步,进入下一次迭代计算。
4 实验验证
为验证DFWA-VNS算法的有效性,选取两类经典的JSP算例[14]:FT类,包括FT06、FT10和FT20;LA类,包括LA05、LA25和LA40。共6种典型问题作为测试算例。并与粒子群算法[15]、遗传算法、FWA算法[9]进行对比试验。4种算法种群规模均为30,迭代计算100次,对每一个算例独立计算20次,取平均值作比较。计算结果见表1,其中:C*表示理论最优解;Aavg表示计算所得平均值;tavg表示平均收敛时间。
由表1可知,本文所提算法DFWA-VNS能计算得到理想结果,同时在每一个算例计算时,均能快速收敛。在求解轻量级问题时,FWA性能同样较优,但是,针对大规模问题的求解时,计算结果并不太理想,容易早熟,领域并未充分搜索。DFWA-VNS算法具有很好的搜索质量,在多次计算过程中均能接近理论最优值,表明该算法鲁棒性较好。DFWA-VNS引入动态调整策略,使得算法可以根据进化状态调整需更新维度,加快收敛速度,同时动态调整策略的引入也是算法具有较优全局寻优能力的重要原因之一。

表1 计算结果
5 结 语
本文提出了一种求解JSP问题的变邻域动态烟花算法,该算法通过变邻域搜索改进烟花算法的搜索方式,加强每一次迭代计算过程中个体之间的相互联系与相互学习,增强了算法的全局寻优能力。同时,引入进化速度概念,并利用进化速度动态调整每一次迭代计算需要更新的维度,避免算法陷入局部最优,同时加快算法收敛速度。通过对6个经典算例的求解,验证了DFWA-VNS算法的有效性。
参考文献(References):
[1]Jain A S, Meeran S. Deterministic job-shop scheduling: Past, present and future[J]. European Journal of Operational Research, 1999, 113(2):390-434.
[2]Tan C J, Neoh S C, Lim C P,etal. Application of an evolutionary algorithm-based ensemble model to job-shop scheduling[J]. Journal of Intelligent Manufacturing, 2017,27:1-12.
[3]赵诗奎, 王林瑞, 石飞. 作业车间调度问题综述[J]. 济南大学学报(自然科学版), 2016(1):74-80.
[4]Kim H C, Boo C J. Intelligent optimization algorithm approach to image reconstruction in electrical impedance tomography[C]//Advances in Natural Computation. Springer Berlin Heidelberg, 2006:856-859.
[5]Heinonen J, Pettersson F. Hybrid ant colony optimization and visibility studies applied to a job-shop scheduling problem[J]. Applied Mathematics & Computation, 2007, 187(2): 989-998.
[6]Chen M, Li J L. Genetic algorithm combined with gradient information for flexible job-shop scheduling problem with different varieties and small batches[C]//MATEC Web of Conferences. EDP Sciences, 2017, 95: 10001.
[7]杨小东, 康雁, 柳青,等. 求解作业车间调度问题的混合帝国主义竞争算法[J]. 计算机应用, 2017, 7(2):517-522.
[8]姚远远, 叶春明. 作业车间调度问题的布谷鸟搜索算法求解[J]. 计算机工程与应用, 2015, 51(5):255-260.
[9]Tan Y, Zhu Y. Fireworks algorithm for optimization[C]// International Conference on Advances in Swarm Intelligence. Springer-Verlag, 2010:355-364.
[10]Gao H, Diao M. Cultural firework algorithm and its application for digital filters design[J]. International Journal of Modelling, Identification and Control, 2011, 14(4): 324-331.
[11]Rahmani A, Amine A, Hamou R M,etal. Privacy preserving through fireworks algorithm based model for image perturbation in big data[J]. International Journal of Swarm Intelligence Research (IJSIR), 2015, 6(3): 41-58.
[12]朱晓东, 刘冲, 郭雅默. 基于烟花算法与差分进化算法的模糊分类系统设计[J]. 郑州大学学报(工学版), 2015, 36(6):47-51.
[14]王成龙, 李诚, 冯毅萍,等. 作业车间调度规则的挖掘方法研究[J]. 浙江大学学报(工学版), 2015, 49(3):421-429.
[15]Kennedy J, Eberhart R. Particle swarm optimization[C]// IEEE International Conference on Neural Networks, 1995. Proceedings. IEEE Xplore, 1995:1942-1948.
