芯层几何构形对复合材料波纹夹层结构冲击特性的影响

骆 伟，谢 伟，刘敬喜

(1.中国舰船研究设计中心,武汉 430064) (2.华中科技大学 船舶与海洋工程学院,武汉 430074)

波纹夹层结构是由两个强度较高的薄面板以及中间轻质波纹芯层组成的一种混杂复合材料夹层结构．与蜂窝夹层结构、泡沫夹层结构、点阵夹层结构相比,波纹夹层结构具有较高的纵向弯曲性能,以及在抗剪切、抗扭等方面具有较为平衡的力学性能和较高的承载效率(极限承载能力与结构重量之比),因此，在航空航天、汽车、船舶等领域的应用越来越多．

近年来,国内外广大研究人员针对金属波纹夹层结构力学性能开展了大量的研究工作,对金属波纹芯层结构的构型如三角形、梯形、矩形等进行了较为深入的分析[1]．文献[2]中将芯层简化为连续介质,对芯层为三角形形式的波纹夹层结构的面内拉伸、面内剪切和弯曲性能进行了研究；文献[3-4]中 采用试验和数值模拟2种方法对梯形芯层波纹夹层结构的冲击及面压缩性能进行了研究，获得了梯形波纹夹层结构的抗冲击特性和面内压缩特性．文献[5-6]中针对梯形芯层波纹夹层结构在冲击载荷作用下的吸能特性开展了较为系统的试验和数值模拟分析,探讨了冲头形状以及冲击能量对波纹夹层结构低速冲击特性的影响;文献[7]中研究了复合材料梯形芯层波纹夹层板在面压力作用下的极限强度,并针对几何尺寸、铺层等参数进行了多目标优化分析;文献[8]中运用有限元和试验方法研究了矩形芯层波纹夹层板在冲击与面载荷作用下的力学性能;文献[9]中运用简化解析方法和有限元方法研究了圆弧组合型芯层波纹夹层板的弯曲极限强度；文献[10]中采用实验和数值模拟方法对复合材料点阵结构的低速冲击特性开展了研究；文献[11]中对X、Y、V形3种夹芯舱壁结构的抗侵彻性能进行了研究,得到了最优夹芯结构型式．文中首先对复合材料面板铝合金波纹夹层结构在低速冲击下的响应特性进行实验研究和数值模拟,然后在芯层重量一致的前提下,设计了几种几何构型不同芯层的波纹夹层结构,并对其冲击特性进行了数值模拟．结果表明:在低能冲击情况下,芯层的刚度越大,结构的吸能越多,结构的局部损伤也较严重．而较弱的芯层刚度因弹性较大,减小了结构对动能的吸收,降低了冲击位置附近的损伤．在高能冲击情况下,芯层被穿透,波纹夹层结构的损伤区域主要位于冲击位置附近,因而芯层几何构型对波纹夹层结构的高能冲击特性影响较小．

1 试验研究及仿真模拟

1.1 模型试件

波纹夹层结构试件由碳纤维面板和铝合金波纹芯层组成．试件尺寸为96 mm×96 mm×14.85 mm(长×宽×高)．碳纤维面板为T700/3234预浸料制成(单层厚度为0.125 mm),铺层顺序为[0/90°/0/90°],面板厚度为1 mm．波纹芯层由2A12-T4铝合金板材制成,每种试样的芯层均包含3个单胞,芯层的高度为12.85 mm;芯层重量为17.6 g．所制备的试件如图1．

图1 梯形波纹的形状和制备的波纹夹层结构试件

1.2 实验装置

冲击试验在落锤试验机上进行,试验机可通过调节落锤高度调节冲击能量,落锤冲击机见图2．冲头安装在落锤下方,冲头由淬火钢材制成,可近似为刚体．试验机上设置上下夹具以约束波纹夹层结构,夹具尺寸、约束力与有限元模型中的设置保持一致．测试数据主要包括冲击力—时间曲线、吸收能量—时间曲线、位移—时间曲线等,由专用的数据采集系统完成采集．

图2 落锤冲击试验机

1.3 数值计算方法

采用ABAQUS有限元程序进行数值计算．建立有限元计算模型(图3),几何模型包括冲头、上夹具、下夹具、波纹夹层结构试样．冲头前端为一个直径为12 mm的半球,后端为一个直径为12 mm、轴向长度为18 mm的圆柱．为提高计算效率,芯层和面板的粘接通过“Tie”约束绑定,绑定区域不发生相对运动和变形[10]．

在计算中,将铝合金芯层材料定义为弹塑性材料,其损伤演化由ABAQUS软件自带的Ductile Damage定义,不考虑其应变率效应的影响．铝合金的密度为2 700 kg/m3,杨氏模量为70 GPa,泊松比为0.3,屈服极限为460 MPa,塑性应力τ-应变ε见图4;碳纤维单层预浸料的基本力学性能见表1．

图3 梯形芯层夹层结构的有限元计算模型

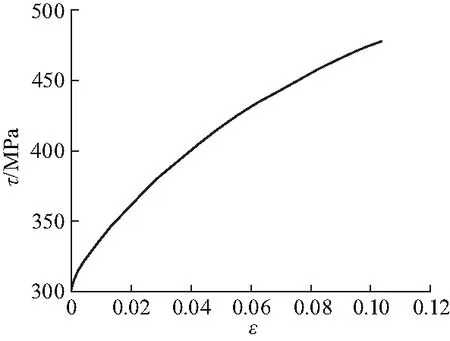
图4 铝合金板材2A12-T4的应力-应变曲线

基于Hashin准则,依据纤维增强的树脂基材料常用的失效模式引入相应的损伤变量,建立损伤刚度矩阵,采用刚度退化的方法表征层合板的损伤演化历程[5,10]．基于Fortran语言,编制用于定义复合材料破坏准则的VUMAT用户子程序,在计算时由ABAQUS程序自动调用．

表1 T700/3234碳纤维预浸料的基本力学性能

注：E11、E22、E23分别为纵向、横向、面外弹性模量；v12、v13、v23为泊松系数；G12、G13、G23分别为1-2、1-3、2-3方向的剪切模量；Xt、Xc、Yt、Yc、Zt分别为纵向拉伸、纵向压缩、横向拉伸、横向压缩、面外拉伸强度；s12、s23、s13为剪切强度；ρ为密度.

为与试验的边界条件保持一致,在波纹夹层结构的上下两端分别设置一个中间开有直径75 mm圆孔的上下夹具,并在上夹具表面施加0.02 MPa的预紧力．冲头的质量为13.26 kg,与冲击试验机冲头保持一致．计算中通过定义冲头的初速度定义冲击能量,在验证算例中冲击能量为20 J,冲击初速度为1.74 m/s．

1.4 结果及对比分析

图5为冲击力F、冲头速度v及能量E的数值模拟结果与试验结果的曲线比较．图6为仿真分析及试验结果照片．图5的曲线结果表明，计算结果与试验结果吻合较好,冲击载荷峰值较为接近,能量变化趋势基本保持一致．结合图6的仿真过程图可以看出整个冲击过程可分为5个阶段:

(1) 冲击开始,芯层铝材与面板共同承受载荷,直至芯层腹板屈曲、冲击力F达到第一个峰值,见图6(a);

(2) 芯层发生屈曲,承载能力迅速下降,此时主要由碳纤维面板及芯层的面板承力,冲击力在略微下降之后继续上升直至最大值(第二个峰值);

(3) 芯层铝板与碳纤维面板相继断裂,见图6(b),裂纹持续扩展,冲击力达到峰值后急剧降低;

(4) 碳纤维面板及铝合金芯层完全撕裂,冲头继续向下运动,面板变形吸能,冲击力呈现一个较长的“平台期”,直至冲头速度v为零(冲头停止,动能完全转化为内能E,内能达到峰值),结构达到最大变形,见图6(c);

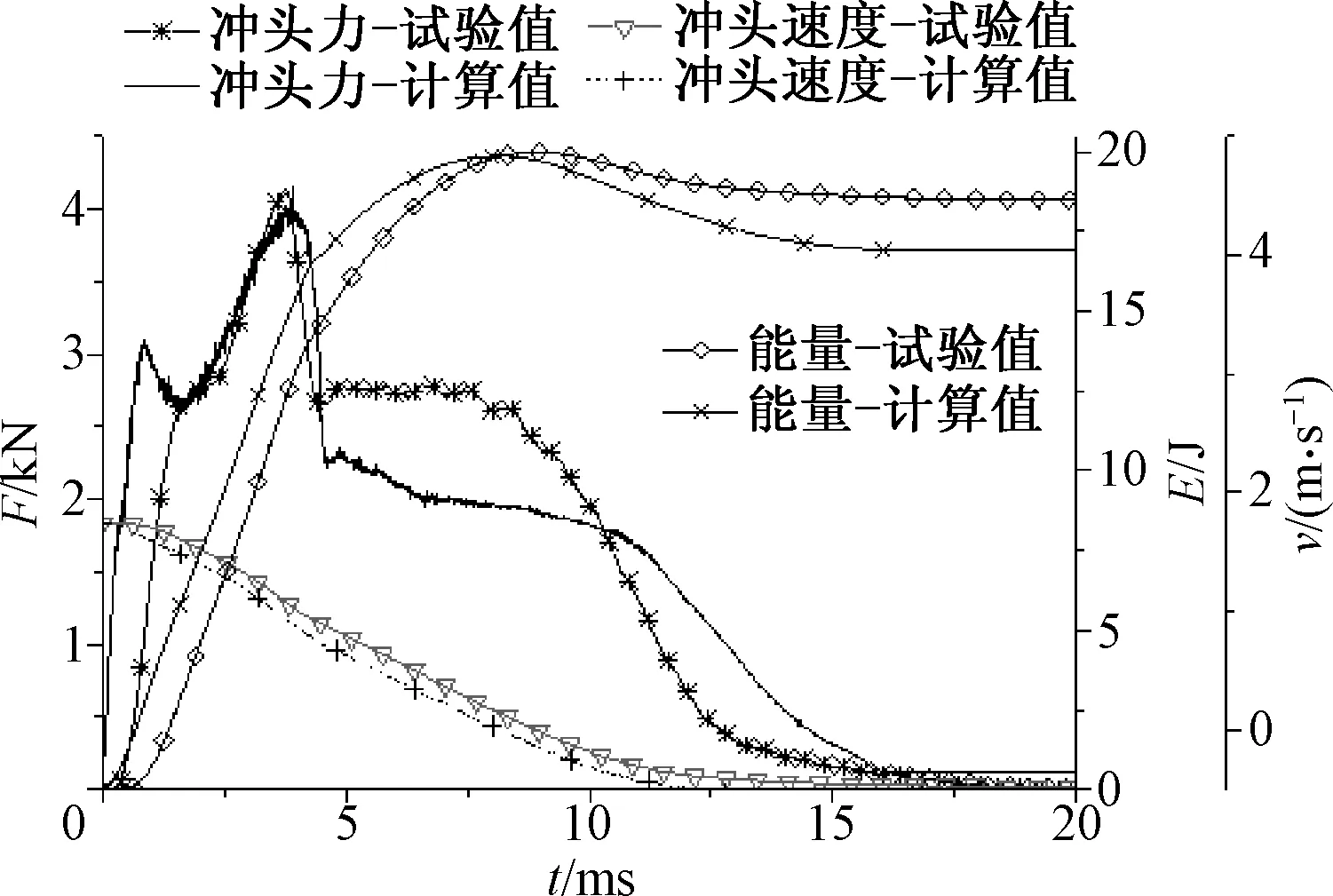
图5 20J冲击能量的结果对比

图6 同时刻有限元仿真模拟结果

(5) 冲头开始反弹,同时冲击力减小,系统内能呈现下降趋势,直至冲头与夹层结构完全脱开,冲击力下降为0,内能趋于稳定,冲击过程结束,见图6(d)．

2 冲击特性分析

2.1 不同几何构型芯层的波纹夹层结构设计

通过改变芯层板厚以维持芯层的重量不变,设计如图7所示的三角形、余弦形、圆弧组合形、梯形和矩形芯层波纹夹层结构,芯层厚度分别为0.55、0.54、0.51、0.5、0.39 mm．

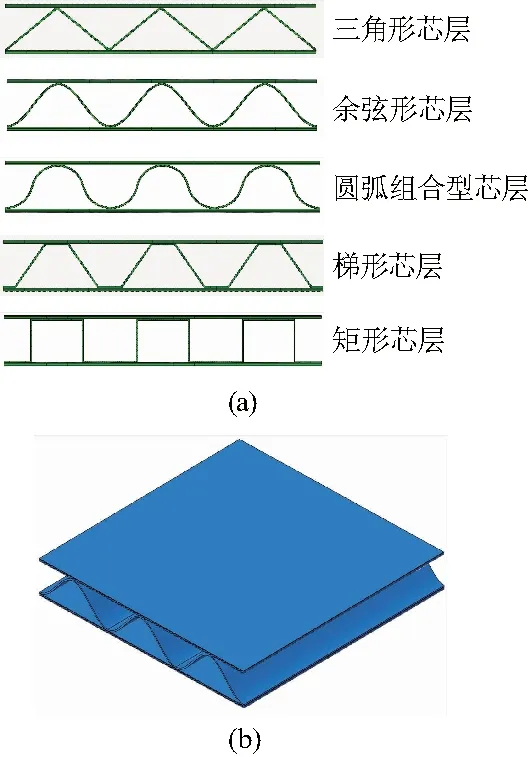
图7 芯层不同几何构型的波纹夹层结构示意

2.2 仿真模拟结果及分析

对5种不同芯层形状的波纹夹层结构进行冲击模拟,冲击能量为20 J,冲击速度为1.74 m/s．图8、9分别为冲击力F—时间t曲线及内能E—时间t曲线,5种不同形状芯层的破坏模式见图10～14．从图8、9给出的冲击力—时间曲线，结合芯层的破坏模式图片可以看出:

(1) 在冲击起始阶段,芯层铝材与面板共同承受载荷．余弦形芯层与圆弧组合形芯层因刚度较小,整体变形较为明显,因而并未出现腹板屈曲和冲击力降低现象;而其余3种形状芯层的夹层结构的腹板均存在明显的屈曲现象,其中三角形芯层因其跨距大最先屈曲,矩形芯层则最后发生屈曲,且其第一个峰值载荷也是5种芯层中最大的．

(2) 随着冲击的继续,面板裂纹形成并扩展,5种芯层的波纹夹层结构的冲击力均下降,其中矩形芯层与梯形芯层的下降幅度较大,其余3种下降幅度较小．结合图10～14中可看出：由于矩形芯层和梯形芯层拥有较大的垂向刚度,冲击区域两侧的芯层单胞成为面板的强边界,使得面板的变形与吸能主要分布在两个单胞之间,面板裂纹扩展后冲击力维持在较低的“平台期”;余弦形芯层与圆弧组合形芯层垂向刚度较小,受垂向力作用时发生弯曲变形,因此面板的弹性变形吸能区域较大,面板裂纹扩展后冲击力的“平台期”高于矩形芯层和梯形芯层;而三角形芯层虽具有较大的垂向刚度,但相邻两侧的单胞间距较大,其面板的变形区域也比矩形和梯形芯层大,冲击力的平台期也相应地大于二者．芯层单胞的刚度差异及单胞跨距差异的共同作用,造成了面板撕裂后“平台区”冲击力的差异．

图8 不同几何构型的波纹夹层 结构冲击力-时间历程曲线

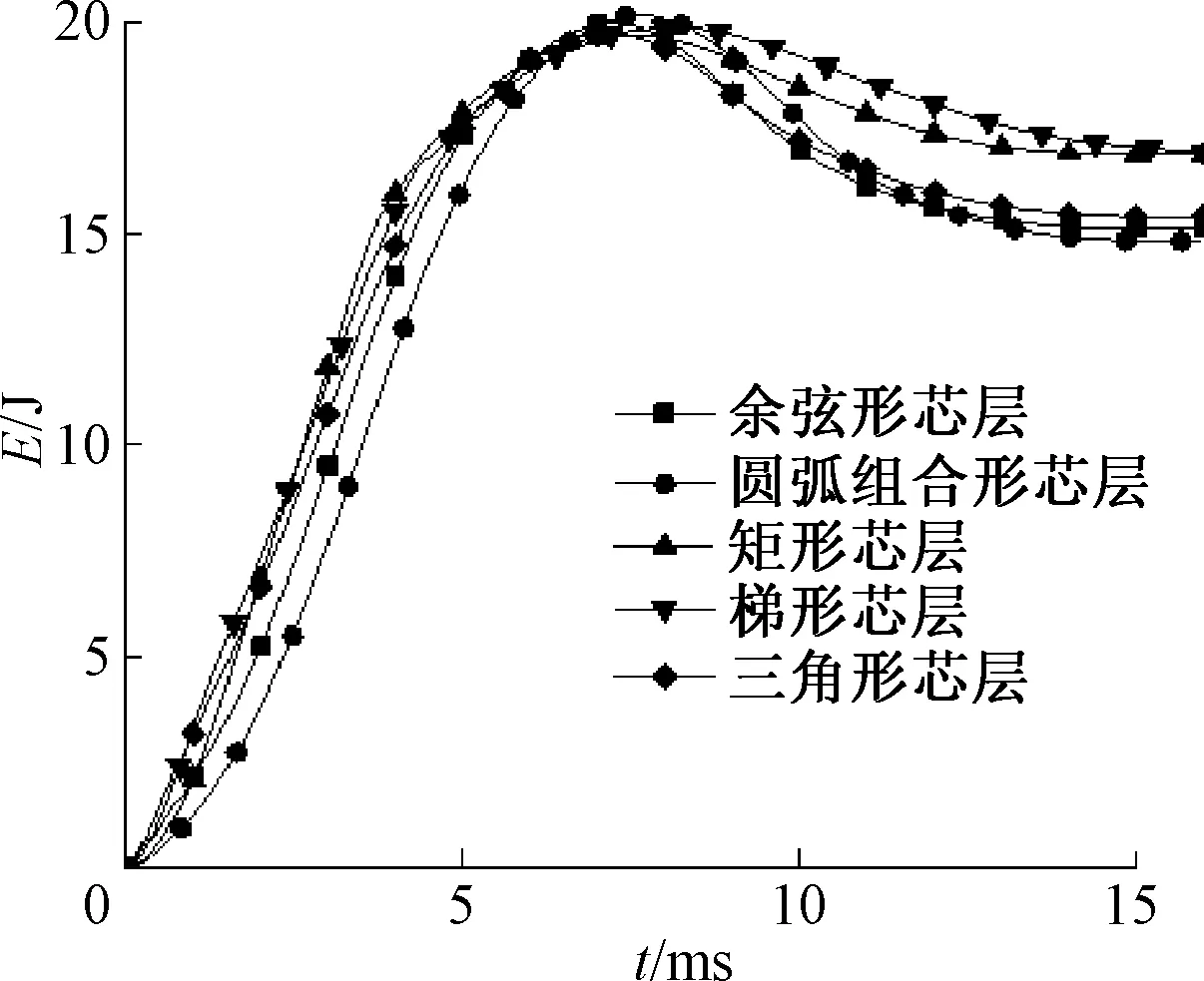
图9 不同几何构型的波纹夹层结构能量-时间历程曲线

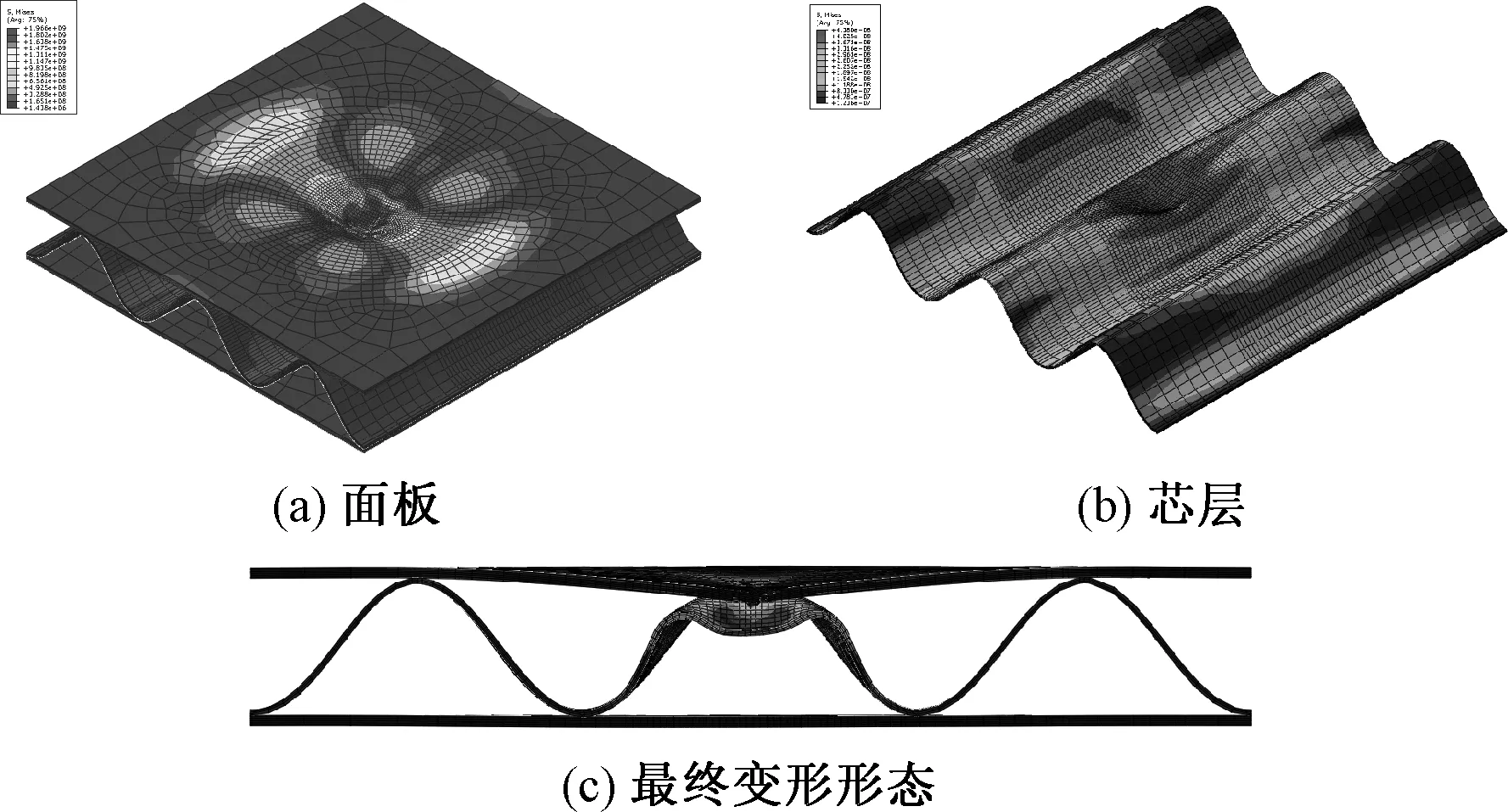
图10 余弦形芯层破坏模式

(3) 冲击过程结束后,余弦形、圆弧组合形芯层的弹性变形区域较大,因而位于中间的芯层单胞未发生明显的断裂;其余3种芯层则产生较严重的断裂．但是,因余弦形、圆弧组合形和三角形芯层与面板间的粘接区域较小,从而使得其面板回弹后会造成芯层的撕裂．

综上所述,在同样的冲击能量下,余弦形与圆弧组合形芯层结构的面板因弹性变形区域较大,从而使得冲击部位损伤较小,结构的最终吸能较小．而矩形、梯形和三角形芯层的刚度较大,因而冲击力较大,但由于限制了面板参与弹性变形的区域,从而使得在冲击部位损伤区域较大,结构最终的吸能较大．

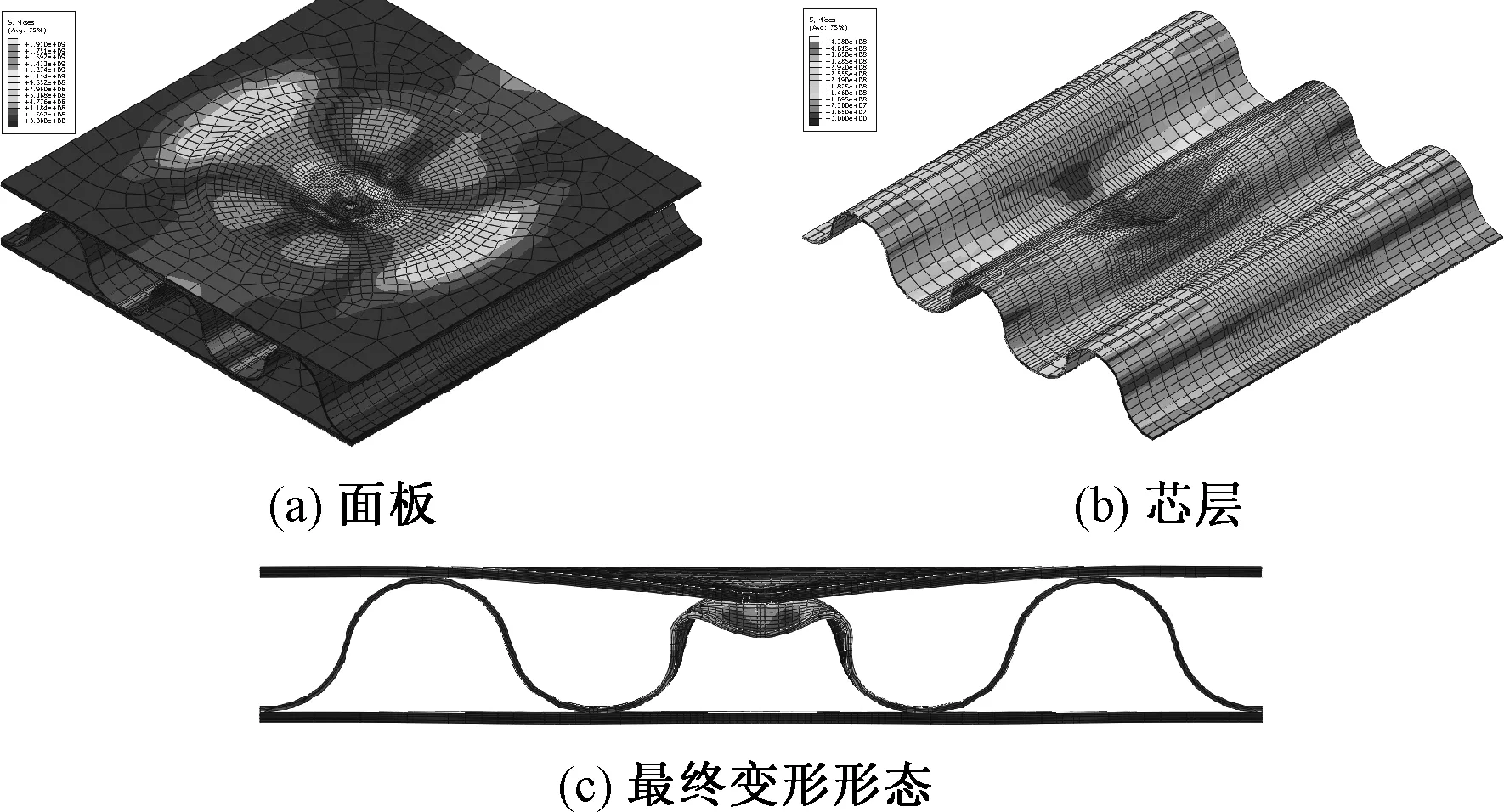
图11 圆弧组合形芯层破坏模式

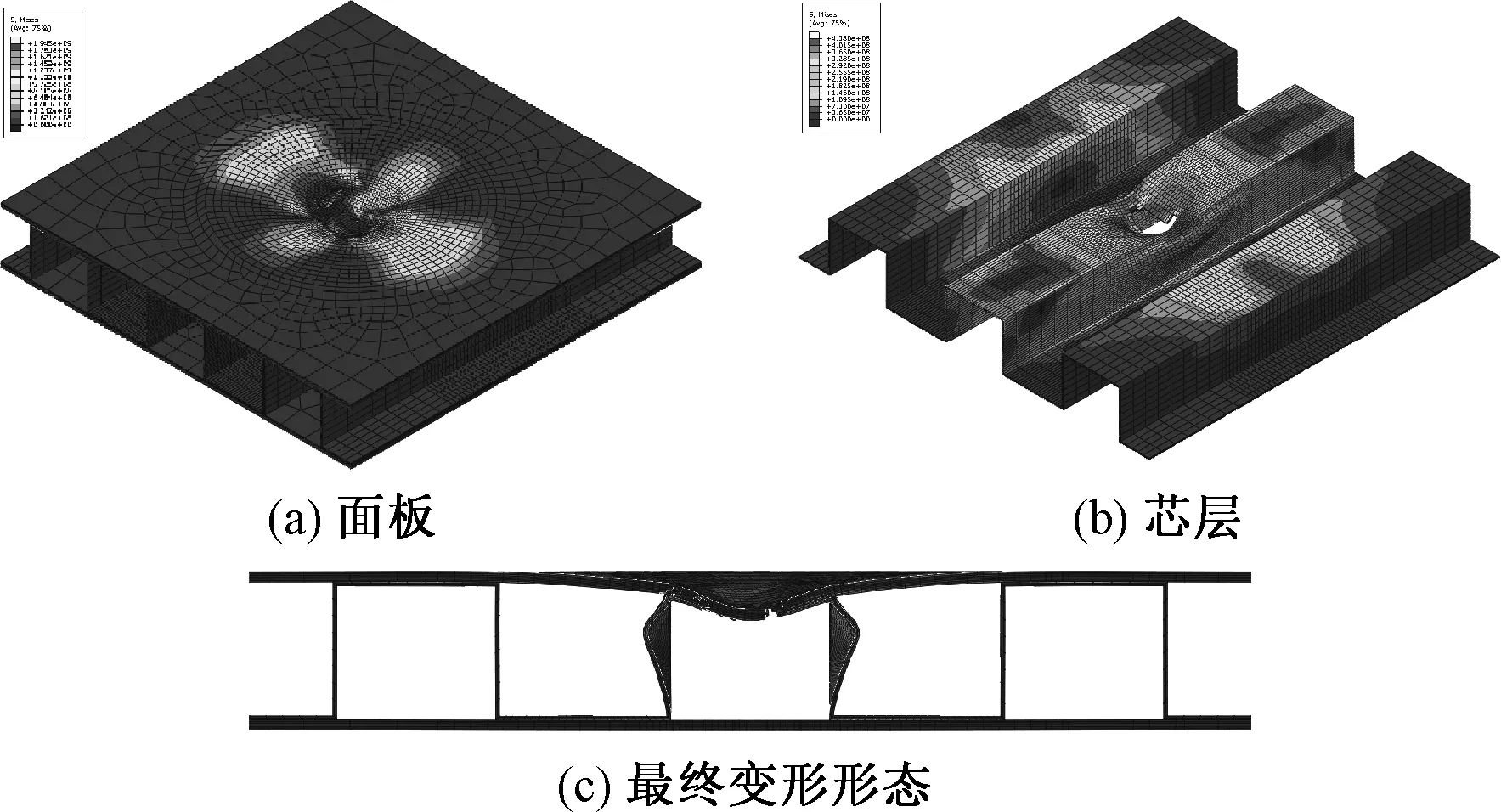
图12 矩形芯层破坏模式

图13 梯形芯层冲击破坏模式

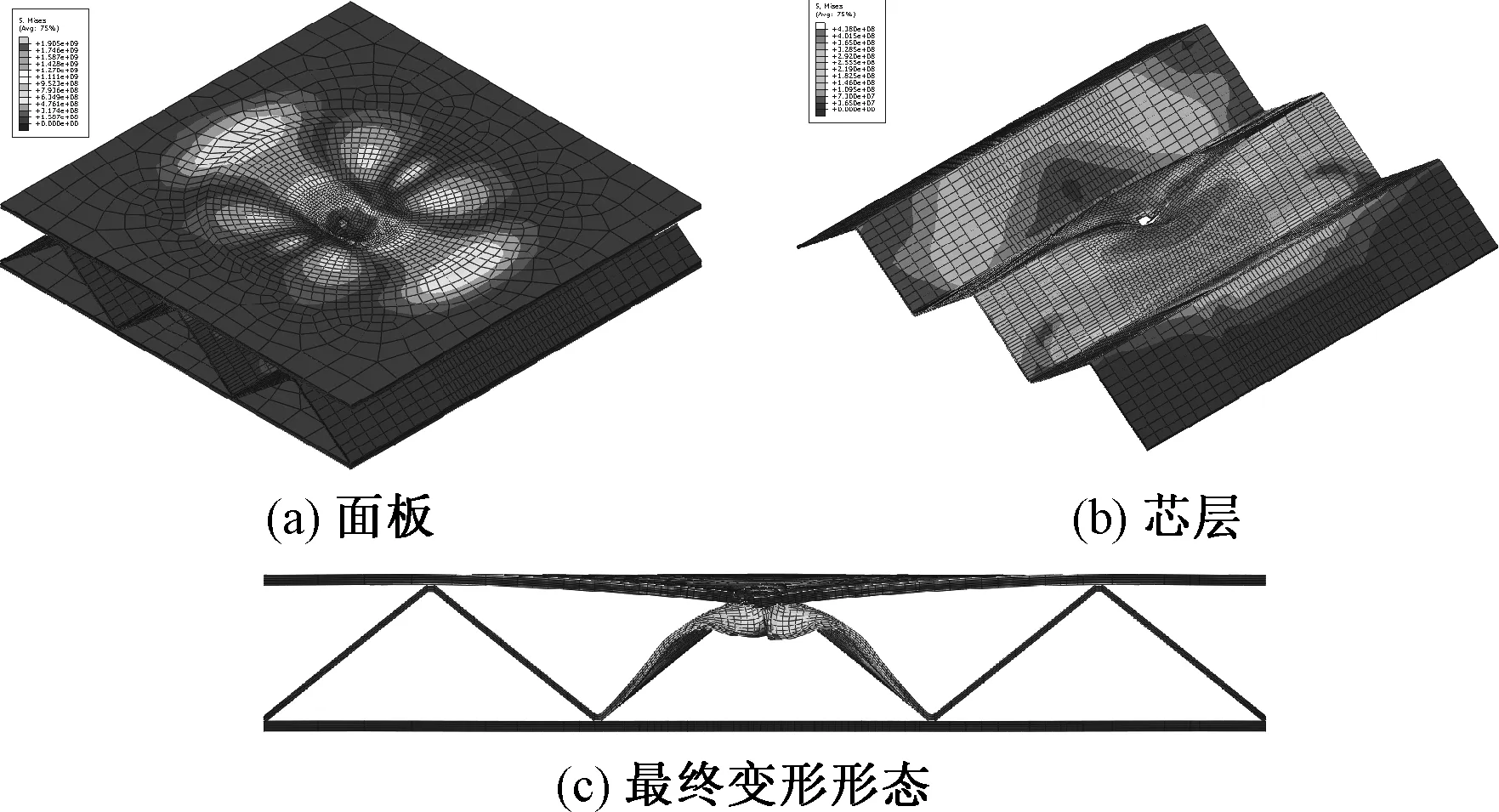
图14 三角形芯层冲击破坏模式

2.3 仿真模拟结果及分析

当冲击能量为50 J时,冲击速度为2.75 m/s,图15为冲击力-时间曲线及内能-时间曲线．图16为5种形状芯层的夹层结构的最终破坏仿真结果．

从图15可以看出：当5种形状芯层的夹层结构遭受50 J能量冲击时,上下面板均被穿透,冲击力—时间曲线和能量—时间曲线基本一致,2个较大的峰值分别对应上下面板被击穿的过程．与20 J低能冲击不同,在50 J能量的冲击下,5种波纹夹层结构均被穿透．破坏模式主要是面板断裂、芯层屈曲、芯层断裂等,损伤区域位于冲击位置附近,芯层的几何形状对能量吸收特性并无显著影响．

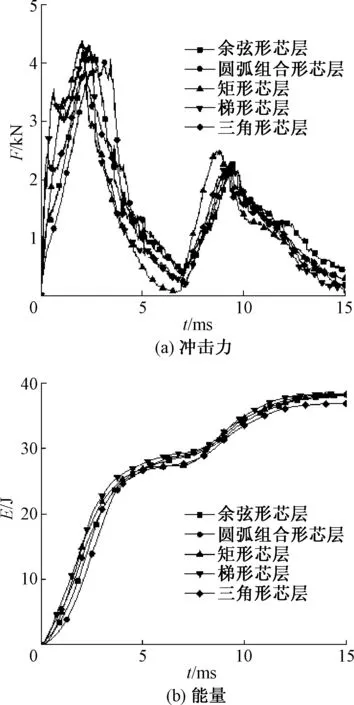
图15 冲击能量为50 J时不同几何构型的波纹夹层结构

图16 5种芯层的结构在50 J冲击能量下的最终变形

3 结论

(1) 基于VUMAT用户子程序的数值计算结果与试验结果吻合较好,该计算方法能有效地预测波纹夹层结构的低速冲击响应特性．

(2) 不同芯层几何构型的复合材料波纹夹层结构的刚度差异较为明显,在不同冲击能量下,其动力响应特性和吸能特性有较大的差别：① 低能冲击下,对于余弦形和圆弧组合形芯层的波纹夹层结构,因刚度较弱,其整体弹性变形较为明显,从而使得结构损伤范围小,最终的吸能也较小;而对于三角形、梯形和矩形芯层的波纹夹层结构,其刚度较大,弹性变形不明显,从而使得其局部损伤较大,最终吸能较大；② 高能冲击下,由于冲击速度较快,刚度对结构动力响应特性和吸能特性的影响很小,从而使得5种不同几何构型芯层的波纹夹层结构动力响应特性和吸能特性基本相同．

References)

[1] 张培文. 冲击载荷作用下固支夹芯圆板的力学行为研究[D]. 太原:太原理工大学, 2013:56-68.

[2] BUANNIC N, CARTRAUD P, QUESNEL T. Homogenization of corrugated core sandwich panels[J]. Composite Structures, 2003, 59(3): 299-312. DOI:10.1016/s0263-8223(02)00246-5.

[3] KILIÇASLAN C, GÜDEN M, ODACI Ï K, et al. The impact responses and the finite element modeling of layered trapezoidal corrugated aluminum core and aluminum sheet interlayer sandwich structures[J]. Materials & Design, 2013(46): 121-133. DOI:10.1016/j.matdes.2012.09.059.

[4] KILIÇASLAN C, GÜDEN M, ODACI Ï K, et al. Experimental and numerical studies on the quasi-static and dynamic crushing responses of multi-layer trapezoidal aluminum corrugated sandwiches[J]. Thin-Walled Structures, 2014(78):70-78. DOI:10.1016/j.tws.2014.01.017.

[5] HE W, LIU J, TAO B, et al. Experimental and numerical research on the low velocity impact behavior of hybrid corrugated core sandwich structures[J]. Composite Structures, 2016(158): 30-43. DOI:10.1016/j.compstruct.2016.09.009.

[6] LIU J, HE W, XIE D, et al. The effect of impactor shape on the low-velocity impact behavior of hybrid corrugated core sandwich structures[J]. Composites Part B: Engineering, 2017(111): 315-331. DOI:10.1016/j.compositesb.2016.11.060.

[7] 郑亚雄. 复合材料梯形波纹夹层板的优化设计[J]. 直升机技术, 2011(2): 15-19. DOI:10.3969/j.issn.1673-1220.2011.02.002.

ZHENG Yaxiong. Optimal design of composite sandwich structure with a trapezoid corrugated core[J]. Helicopter Technique, 2011(2): 15-19. DOI:10.3969/j.issn.1673-1220.2011.02.002.(in Chinese)

[8] HOU S, ZHAO S, REN L, et al. Crashworthiness optimization of corrugated sandwich panels[J]. Materials & Design, 2013(51): 1071-1084. DOI:10.1016/j.matdes.2013.04.086.

[9] BARTOLOZZI G, PIERINI M, ORRENIUS U, et al. An equivalent material formulation for sinusoidal corrugated cores of structural sandwich panels[J]. Composite Structures, 2013(100): 173-185. DOI:10.1016/j.compstruct.2012.12.042.

[10] 张国旗. 复合材料点阵结构吸能特性和抗低速冲击性能研究[D]. 哈尔滨：哈尔滨工业大学, 2014.

[11] 尹群, 王海, 王珂, 等. 侵彻载荷作用下船体新型夹芯双层舱壁结构型式研究[J]. 江苏科技大学学报(自然科学版), 2016, 30(2): 103-108,114. DOI:10.3969/j.issn.1673-4807.2016.02.001.

YIN Qun, WANG Hai, WANG Ke, et al. Study on the structure of new sandwich double bulkhead of ship under penetration load[J].Journal of Jiangsu University of Science and Technology(Natural of Science Edition), 2016, 30(2): 103-108,114. DOI:10.3969/j.issn.1673-4807.2016.02.001.(in Chinese)