基于颗粒阻尼技术的海洋平台桁架结构振动特性研究
2018-04-11夏兆旺茅凯杰邵广申方媛媛
夏兆旺,茅凯杰,薛 程,邵广申,方媛媛
(江苏科技大学 能源与动力工程学院,镇江 212003)
近年来随着我国经济的持续高速增长,对油气资源的需求越来越紧张,使得近海石油天然气资源的开发越来越重要.海洋平台作为海洋油气资源开发的基础性设施,是海上生产作业和生活的基地,其安全性至关重要[1-2].海洋平台不可避免受到风、海浪、洋流、甚至是地震荷载的联合作用,长期处在这样恶劣的外在环境中,会导致海洋平台在使用过程中发生明显持续的振动,从而加剧平台的疲劳破坏,降低系统的可靠度,影响结构的安全性和耐久性.桁架结构是海洋平台中最常见的一种结构形式,其振动控制技术已经受到了越来越多的关注,目前常采用的粘弹性阻尼减振技术具有较好的减振效果[3-4],但由于减振装置长期暴露在盐雾和高强度的紫外线辐射下,粘弹性阻尼材料容易老化、失效,其使用年限有限.因此,急需一种能适应腐蚀性环境的阻尼减振技术.
颗粒阻尼技术是在振动结构的合适部位加工一系列孔洞,在孔洞中填充适当数量的颗粒,随着结构体的振动,通过颗粒之间以及颗粒与结构体之间的碰撞和摩擦消耗结构体的能量,实现减振的目的[5].颗粒阻尼技术的优点是:结构简单,不需要改变原有结构的外形尺寸[6-7];减振频带宽,耐高温、抗老化;噪声小,减振效果好[8-10].由于颗粒阻尼器的优良性能,目前颗粒阻尼减振技术已经应用于汽车、建筑、航空航天等领域.颗粒阻尼的优点能很好的与桁架结构进行有机结合,如利用桁架结构的孔腔设计颗粒阻尼器.
由于颗粒阻尼的强非线性[11-12],给其理论分析带来了很大的难度,目前还没有形成统一颗粒阻尼器设计指导方法.文中将基于离散元和有限元的耦合仿真算法,分析带颗粒阻尼器的海洋平台桁架结构的动力学特性,研究颗粒密度、填充率、孔径粒径比(孔腔直径与颗粒直径的比值)、激振力频率和幅值等参数对减振效果的影响,并进行试验验证.研究颗粒阻尼技术在桁架结构减振领域的应用,为解决长期处于强紫外线环境中的海洋平台结构的减振降噪提供一种新的方法.
1 颗粒阻尼仿真方法
离散元方法把系统内颗粒看为离散的颗粒单元组合,每个颗粒视为一个基本单元,通过各个单元之间的接触力和牛顿第二运动定律描述颗粒的运动行为.其运算法则以颗粒运动方程的有限差分为基础,以颗粒间的接触模型为理论核心.文中应用DMAP语言对大型工程有限元软件NASTRAN进行二次开发,通过MATLAB将离散元法与有限元法结合,发挥有限元分析连续结构和离散元分析散体结构的特长.
1.1 颗粒接触力学模型
颗粒在颗粒阻尼器内运动会发生相互之间的碰撞和摩擦,产生接触力,进而影响颗粒的运动.主要仿真圆球形状颗粒,判断颗粒间发生接触的条件是两颗粒球球心之间的距离小于两颗粒球的半径之和.圆球形颗粒接触时的相对运动分为法向运动、切向运动和转动3种.由于两颗粒相互接触的面积很小,因此两颗粒球相对转动引起的力矩可忽略,所以主要考虑颗粒间的法向和切向接触力.两颗粒相互之间的接触力模型可简化为弹簧-阻尼器-滑块模型,如图1.其中,弹簧代表颗粒之间的弹性,阻尼器代表颗粒之间的粘性,滑块代表颗粒之间的摩擦.
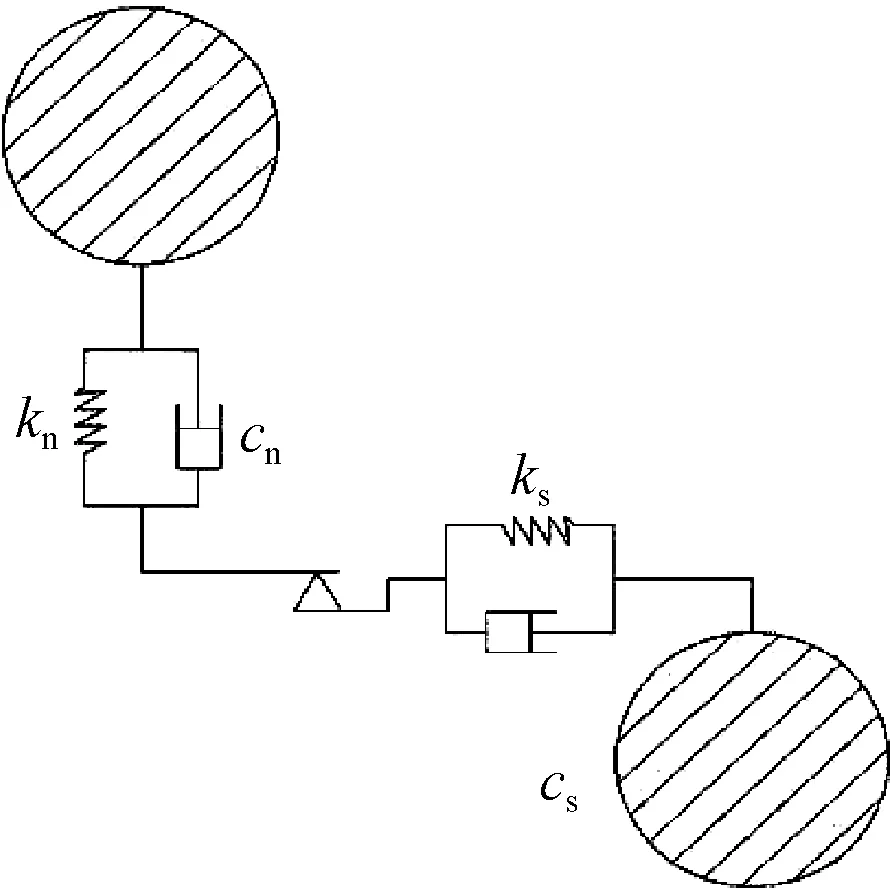
图1 颗粒接触模型
颗粒间法向接触力用赫兹粘弹性模型表示:
(1)
式中:kn为颗粒间法向刚度系数,cn为颗粒间法向阻尼系数,δn为颗粒间的叠合量.
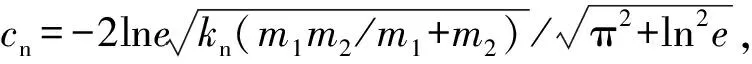
颗粒间切向接触力通过切向位移增量与力增量表示:
Fs(t)=Fns(t-Δt)+ksvsΔt+csvs
(2)
颗粒相互运动过程中,切向力要同时满足库仑定律:
(3)
式中:ks为颗粒间的切向刚度系数;cs为颗粒间的切向阻尼系数;Fs(t)为t时刻两颗粒间的切向接触力;Fns(t-Δt)为t-Δt时刻两颗粒间的切向接触力,Δt为计算时间步长;ks为两颗粒间的切向刚度系数
1.2 颗粒接触时间步长
仿真计算中,要取很小的时步以保证一个时步内颗粒的动量只能传播给临近的颗粒,以及颗粒加速度近似恒定.通过瑞利波沿颗粒表面的传播速度得到时步为:
(4)
式中:G为颗粒的剪切模量,ρ为颗粒密度,γ为泊松比,Rmin为最小颗粒半径.
当颗粒与周围接触的颗粒数大于等于4个时,时步取公式中的20%;当颗粒与周围接触的颗粒数小于4个时,时步取公式中的40%.
1.3 颗粒运动方程
根据颗粒间的接触力采用牛顿第二运动定律建立颗粒运动方程,运用动态松弛法对颗粒运动方程进行循环迭代计算,在每一个时步更新各个颗粒的位置.通过对颗粒阻尼器中每个颗粒的微观运动过程进行跟踪研究,计算所有颗粒对振动结构的宏观作用力.球形颗粒的平动和转动方程为:
(5)
式中:xi(t)为颗粒平动位移、∑F(t)为颗粒受到的合力,mi为颗粒质量,∑M(t)为对颗粒的合力矩,θi(t)为颗粒转动的角位移,Ii为颗粒的转动惯量.
由中心差分法可得t+Δt/2时刻颗粒的速度和加速度
(6)
(7)
Δt时刻后i颗粒移动到一个新位置,并产生新的接触力和接触力矩,重新计算其所受的合力∑F(t+Δt/2) 和合力矩∑M(t+Δt/2)后返回式(7)计算,重复这一过程,即可得到每个颗粒的运动特性.
2 颗粒阻尼桁架结构试验
桁架结构由无缝不锈钢管构成,其中桁架的主柱为直径32 mm的不锈钢管,壁厚3 mm;桁架的加强管和结构管为直径22 mm的不锈钢管,壁厚2 mm,钢管中可以填充金属颗粒;桁架的平台结构为空心结构可填充金属颗粒,由两块3 mm厚的碳钢板材构成,两板材间的距离为20 mm,试验测试如图2.

图2 桁架结构试验装置
在桁架结构上打孔并填充颗粒进行试验测试.颗粒填充率分别为:0、20%、40%、60%、80%和100%;采用90SZ55型电机激励,为增加激励强度,在电机上安装偏心质量块,电机的安装位置分别为桁架结构下层平台正中间位置.电机的转速分别为1 000、2 000和3 000 r/min;填充的颗粒分别为直径0.5、0.8、1、1.5、2和3 mm钢球,钢球密度为7 800 kg/m3;颗粒间及颗粒与孔壁间的弹性恢复系数都为0.78.
2.1 颗粒密度对系统振动规律的影响
电机转速为1 000 r/min,分别填充直径为0.5 mm的钢球和碳化钨颗粒,钢球的密度为7 800 kg/m3,碳化钨的密度为13 600 kg/m3,填充率都为40%,桁架结构的传递率曲线如图3.从图3中可以看出:填充颗粒密度对系统的减振效果有限明显,填充密度较大的碳化钨颗粒时,桁架颗粒阻尼系统的减振效果更好;在0~500 Hz系统响应平均降低了4.7 dB,在500~1 500 Hz系统响应平均降低了7.3 dB,表明在高频段颗粒的密度对系统减振效果影响更加明显.
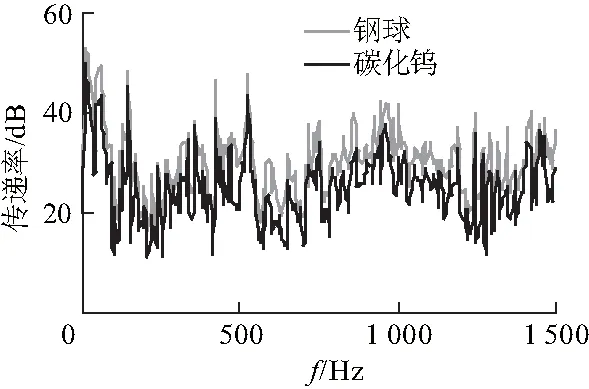
图3 颗粒密度对系统减振效果的影响
2.2 颗粒直径对振动系统的影响
电机转速为1 000 r/min,分别填充填充直径为0.5、1、2、3 mm的钢球,填充率都为40%,桁架结构的传递率曲线如图4.从图4中可以看出:桁架结构的减振效果随着颗粒直径的增加而降低,但是颗粒直径对桁架结构的振动特性影响不明显;填充直径1、2、3 mm颗粒的桁架结构的平均传递率分别比填充填充直径0.5 mm颗粒的桁架结构增加了1.2、2.7、3.1 dB.

图4 颗粒直径对系统减振效果的影响
3 颗粒阻尼桁架结构的振动特性
通过离散元和有限元相结合的方法研究带颗粒阻尼器的海洋平台桁架结构的动力学特性,首先用有限元软件NASTRAN建立桁架结构有限元模型,计算桁架结构在激励下一个时步内的响应,并提取孔腔(颗粒阻尼器)的位移;然后根据孔腔位移用离散元法在MATLAB环境下仿真计算各个颗粒间及颗粒与孔壁间的接触力、一个时步内各个颗粒的位移、速度和加速度;再将颗粒对孔壁的接触力作为边界条件载入到桁架结构下一个时步计算时的有限元模型,计算桁架结构的振动特性,提取孔腔新的位移,如此循环即可计算出桁架结构的响应.
桁架结构仿真与实验振动传递率曲线试验如图5,其中电机转速为1 000 r/min,填充直径为0.5 mm的钢球颗粒,填充率为40%.从图5可以看出:仿真数据与试验数据基本一致,说明文中采用的数值仿真方法是可行的.

图5 桁架结构数值仿真与试验比较
通过仿真与试验对比分析填充率对系统传递率的影响.电机转速为1 000 r/min,填充直径为0.5 mm的钢球,填充率分别为0(不含颗粒阻尼)、20%、40%、60%、80%、100%,桁架结构的传递率曲线如图6.从图6可以看出:填充各种填充率都能在一定程度上降低桁架结构的振动,其中填充率为80%左右时,桁架的传递率最小;填充率为100%时桁架结构的振动仍然小于无填充颗粒时的传递率,此时颗粒的运动碰撞耗能受限,但颗粒间的相互摩擦仍然起到一定的耗能作用.

图6 颗粒填充率对系统减振效果的影响
4 结论
文中研究了海洋平台桁架结构的颗粒阻尼减振特性,采用基于离散元和有限元法的耦合仿真算法进行数值仿真,并试验验证,得到结论如下:
(1) 数值仿真结果与试验结果基本一致,表明采用的耦合仿真算法能满足工程计算需求;
(2) 填充颗粒密度对系统减振效果影响明显,填充碳化钨颗粒比填充钢球颗粒时海洋平台结构传递率在0~500 Hz平均降低了4.7 dB,在500~1 500 Hz平均降低了7.3 dB;
(3) 填充颗粒的直径对海洋桁架结构的振动影响较低,填充直径1、2、3 mm颗粒的桁架结构的平均传递率分别比填充直径0.5 mm颗粒的桁架结构增加了1.2、2.7、3.1 dB;
(4) 填充率为80%左右时,系统的减振效果最好,填充率为100%时颗粒阻尼仍然有一定的减振效果.
References)
[1] XIA Z, WANG X, HOU J, et al. Non-linear dynamic analysis of double-layer semi-active vibration isolation systems using revised Bingham model[J]. Journal of Low Frequency Noise, Vibration and Active Control, 2016, 35(1): 17-24. DOI:10.1177/0263092316628715.
[2] 夏齐强, 楼伟锋, 陈志坚. 双层圆柱壳结构减振设计及模型试验研究[J]. 船舶力学, 2016, 20(1): 148-158. DOI:10.3969/j.issn.1007-7294.2016.h1.018.
XIA Qiqiang, LOU Weifeng, CHEN Zhijian. Study on vibration reduction design for double cylindrical shell and model testing[J]. Journal of Ship Mechanics, 2016, 20(1): 148-158. DOI:10.3969/j.issn.1007-7294.2016.h1.018.(in Chinese)
[3] 夏兆旺, 徐峰, 温华兵, 等. 基于统计能量分析法的高铁轮轨减振降噪研究[J]. 江苏科技大学学报(自然科学版), 2011, 25(4): 354-358. DOI:10.3969/j.issn.1673-4807.2011.04.011.
XIA Zhaowang, XU Feng, WEN Huabing, et al. Study on noise and vibration reduction based on statistical energy analysis method for wheel-rail of high speed railway[J]. Journal of Jiangsu University of Science and Technology(Natural Science Edition), 2011, 25(4): 354-358. DOI:10.3969/j.issn.1673-4807.2011.04.011.(in Chinese)
[4] 夏兆旺, 袁秋玲, 方媛媛, 等. 基于动态子结构-阻抗法的车辆制动鼓动态特性研究[J]. 江苏科技大学学报(自然科学版), 2012, 26(6): 568-571.DOI:10.3969/j.issn.1673-4807.2012.06.010.
XIA Zhaowang, YUAN Qiuling, FANG Yuanyuan, et al. Dynamic response analysis of drum brake based on the substructure modal synthesis method-mechanical impedance method[J]. Journal of Jiangsu University of Science and Technology(Natural Science Edition), 2012, 26(6): 568-571.DOI:10.3969/j.issn.1673-4807.2012.06.010.(in Chinese)
[5] DNJ Els. Damping of rotating beams with particle dampers: experimental analysis[J]. AIAA Journal, 2011, 49(10): 2228-2238. DOI:10.2514/1.j050984.
[6] 夏兆旺, 温华兵, 刘献栋. 基于颗粒阻尼的旋转平板叶片结构动力学特性研究[J]. 振动与冲击, 2014, 33(9): 61-65,88. DOI:10.13465/j.cnki.jvs.2014.09.011.
XIA Zhaowang, WEN Huabing, LIU Xiandong. Dynamic characteristics of a rotating plate structure with particle damping[J]. Journal of Vibration and Shock, 2014, 33(9): 61-65,88. DOI:10.13465/j.cnki.jvs.2014.09.011.(in Chinese)
[7] YAO B, CHEN Q, XIANG H Y, et al. Experimental and theoretical investigation on dynamic properties of tuned particle damper[J]. International Journal of Mechanical Sciences, 2014, 80: 122-130. DOI:10.1016/j.ijmecsci.2014.01.009.
[8] PANOSSIAN H V. Structural damping enhancement via non-obstructive particle damping technique[J]. Journal of Vibration and Acoustics, 1992, 114(1): 101. DOI:10.1115/1.2930221.
[9] HE J, HE C, WU X, et al. Analysis of influences of gearbox flexibility on dynamic characteristics[J]. Zhongguo Jixie Gongcheng/China Mechanical Engineering, 2015, 26(15):2010-2015.
[10] OLSON S E. An analytical particle damping model[J]. Journal of Sound and Vibration, 2003, 264(5): 1155-1166. DOI:10.1016/s0022-460x(02)01388-3.
[11] LU Z, LU X, MASRI S F. Studies of the performance of particle dampers under dynamic loads[J]. Journal of Sound and Vibration, 2010, 329(26): 5415-5433. DOI:10.1016/j.jsv.2010.06.027.
