面向多声源的压缩感知麦克风阵列的波达方向估计

章宇栋,黄惠祥,童　峰

(厦门大学 海洋与地球学院,水声通信与海洋信息技术教育部重点实验室,福建 厦门 361102)

麦克风阵列技术如今已广泛应用于智能机器人、视频会议、可穿戴设备、语音增强等领域．麦克风阵列的语音增强功能主要通过先对声源定位,再对其方位进行波束增强,抑制旁瓣来实现．实际应用中如会议等具有多说话人的场景,语音增强设备需不断重新定位语音增强方向,在此类场景下,如何分辨多人同时说话以及进行定位语音增强成为了新的挑战．

麦克风阵列声源定位技术主要分为3大类:1) 基于最大输出功率的可控波束形成的声源定位技术[1]在实际使用过程中需要进行全局搜索,运算量较大,还会影响到定位的实时性,同时还需要提前得到信号源频谱特性与环境噪声先验知识的关系,因此不易实现；2) 基于高分辨率谱估计的声源定位技术[2]主要运用于窄带信号,对于语音信号这样的宽带信号,会导致算法运算量增加,同样不利于实现；3) 基于互相关时延估计的声源定位技术[3]计算量较小、易实现,但在室内混响严重及低信噪比环境下性能下降严重．

相位变换加权的可控响应功率(SRP-PHAT)定位算法[4]结合了可控响应功率和相位变换加权的优点,比基于时延估计的定位算法具有更好的性能,但在混响和噪声较强的环境下,该声源定位算法性能骤降．此外传统的麦克风阵列针对多声源定位的方法，如时延估计的L型麦克风阵列进行多声源波达方向(DOA)估计[5]以及利用L型的麦克风阵列获得多声源的频率及到达角的联合估计方法[6]，均是采用L型麦克风阵列来获得到达角的空间位置及时延关系，从而对多声源进行定位，而本研究则基于压缩感知(CS)理论对多声源进行定位与分辨．

CS理论最重要的意义在于可以极大地减轻信号采集端的复杂度,在采集端低采样率的情况下,信号的接收端能以比较大的概率重构出原始信号．在水声信道估计中,CS信道估计可利用信道稀疏特性提高估计性能[7]．CS理论突破了原有的奈奎斯特采样定理的束缚,当信号满足稀疏信号的条件时,可线性投影到低维空间上,若CS矩阵满足约束等距性(RIP)条件,则可根据低维的压缩采样信号实现高概率的准确重构[8]．

赵小燕等[9]基于CS的声源定位算法,通过将麦克风接收的信号转换至频域,将声源可能存在的空间位置所对应的房间频域响应定为特征字典,再利用正交匹配追踪(OMP)算法重构出信号,加强声源的位置信息,从而获得更为鲁棒的声源位置估计．在高混响低信噪比的仿真实验条件下,CS-OMP算法的定位性能要明显优于SRP-PHAT算法．但该算法需要事先测量各声源可能存在的空间位置的房间冲激响应,在实际应用背景下仍有较大的不便性[10]．

在CS-OMP算法的基础上,本研究在高混响低信噪比环境下直接利用麦克风阵列阵元间的时延关系构造房间冲激响应,并进行了在此环境下的多说话人声源方位估计的实验．对SRP-PHAT、DS、CS-OMP以及本研究基于构造房间冲激响应CS(CRR-CS)的DOA估计算法在不同信噪比等多种条件下对多声源的分辨能力进行对比和评估．

1　基于CRR-CS的DOA估计算法

1.1　信号模型

对于一个处在室内环境中的M元线性麦克风阵列,第m个麦克风接收到的信号为

xm(n)=hm(rs,n)*s(n)+wm(n)，

m=1,2,…,M,

(1)

其中,*表示卷积运算,n为离散时间序列，s(n)为声源信号,wm(n)为第m个麦克风接收到的噪声,hm(rs,n)为声源位置rs到第m个麦克风的房间冲激响应．

1.2　CS理论

假定N×1维复矢量Y=[Y1,Y2,…,YN]T可用基矩阵Ψ=[Ψ1,Ψ2,…,ΨN]T线性表示为

(2)

其中,S=[S1,S2,…,SN]T表示N×1维的系数矢量．

若矢量S中非零的个数‖S‖0满足

‖S‖0=P≪N,

(3)

则称信号Y为基矩阵Ψ上的稀疏信号．式中,‖·‖为l0范数,P为Y的稀疏度,Ψ为稀疏基．

在CS理论中,若Y在某已知基矩阵Ψ上的系数是稀疏的,则稀疏的信号Y可以线性投影到低维空间上,利用低维的压缩采样信号可高概率地无损重构出高维的原始信号．通常用一个M×N维观测矩阵Φ对信号Y进行线性变换,得到M×1维的观测矢量

X=ΦY=ΦΨS=ΘS.

(4)

其中,X=[X1,X2,…,XM]T(M≪N)为观测矢量,Θ=ΦΨ为CS矩阵．

当随机观测矩阵Φ满足M≥CPlog(N/P)时(C是一个与恢复精度有关的常数),CS矩阵Θ能够以较大概率满足RIP条件．若CS矩阵Θ满足RIP条件,则可实现高概率准确的信号重构[11]．在实际情况中,噪声往往无法避免,需对欠定方程(4)引入加性噪声项,即

X=ΘS+W,

(5)

其中,W为有界噪声．

在Y为稀疏信号的前提条件下,式(5)可以通过l0范数最小化方式求解,即

s.t. ‖X-ΘS‖2≤ε，

(6)

其中,ε是与噪声相关的常量．

CS理论的核心问题是信号的重构,目前已有的重构算法有OMP算法、基追踪(BP)算法等，本研究采用OMP算法．

1.3　DOA估计算法的描述及信号重构

麦克风阵元接收到的信号xm(n)加窗后,经离散傅里叶变换得到频域信号Xm(k)．假如房间冲激响应的长度远小于窗函数的长度,再将其用矢量描述为

X(k)=H(rs,k)S(k)+W(k).

(7)

其中:S(k)为声源信号的频域矢量;X(k)为麦克风接收信号的频域矢量，X(k)=[X1(k),X2(k),…,XM(k)]T;H(rs,k)为声源rs处的房间频域响应矢量，H(rs,k)=[H1(rs,k),H2(rs,k),…,HM(rs,k)]T;W(k)为噪声的频域矢量，W(k)=[W1(k),W2(k),…,WM(k)]T．

声源可能存在的空间位置集为{r1,r2,…，rI},则ri对应的房间频域响应矢量为H(ri,k),假定空域离散位置的个数即稀疏度I，当其远大于目标声源的个数时,则冗余的房间频域响应矩阵为

D(k)=[H(r1,k),H(r2,k),…,H(rI,k)].

(8)

将式(8)中冗余房间频域响应矩阵D(k)称为字典,在此条件下,可将式(7)改写为

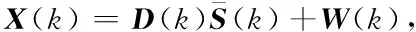
(9)

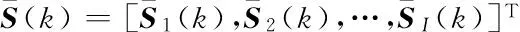
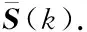
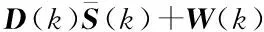
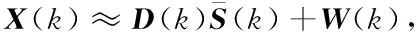
(10)

(11)

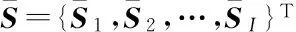
(12)

1.4　时延关系下的CRR

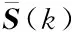
hm(rs,n)=δ(n,tm),

(13)

其中,

(14)

其中,θ为信号入射方向与阵列夹角,c为声速,fs为采样率[13]．

2　实验与分析

2.1　实验设置

实验在空间尺寸约为30 m×20 m×6 m的厦门大学艺术学院音乐厅进行．麦克风阵列为阵元间距13.5 cm的7元均匀线阵,语音信号为TIMIT标准语音信号[14],通过Marshall蓝牙音箱播放,采样率为16 kHz．将2个声源分别放置在阵列前方30°，0°两个方位上进行播放,对比不同算法性能的多声源DOA估计性能．此外利用Marshall蓝牙音箱播放噪声进行实录以用于叠加构成不同信噪比场景．

麦克风阵列的波束方向性函数为[15]:

(15)

其中,N为麦克风数,f为语音段频率,ψ为定位角．波束宽度为主极大值到理论上出现零时的角度,假定入射角θ=90°,f=2 kHz,d=13.5 cm,可以求得理论波束宽度约为21.9°,故实验中将扫描精度设置为15°,略小于理论波束宽度．由于是对多声源进行定位与分辨，双声源若设置间隔太远，则易于分辨；若设置角度间隔小于理论波束宽度，则会导致双声源的信号强度都最大而无法判定是否准确分辨.故双声源角度间隔设置为略大于理论波束宽度的30°．

原始语音信号信噪比为15.66 dB,通过叠加实录的噪声来构造不同信噪比的测试信号,用来对SRP-PHAT、DS，以及CRR-CS算法在不同信噪比条件下对多声源定位估计的分辨性能．其中,通过实测获得的各空间位置到麦克风阵列的冲激响应用于CS-OMP算法构造稀疏恢复方程．算法实验参数设置见表1.

表1　实验参数设置

2.2　实验结果及分析

2.2.1不同信噪比下各算法对多声源的分辨性能

当I=2,η=0.15时,不同信噪比条件下各算法对多声源的分辨能力如图1所示.

从图1可以看出，在不同信噪比条件下CRR-CS算法曲线在不同声源方向都有尖锐的指向性,可见CRR-CS算法对两个声源的方位估计具有很强的分辨能力,且定位效果很好；DS算法能够大致估计出声源的位置,但无法分辨两个不同的声源；SRP-PHAT算法也能够分辨出两个不同的声源位置,但指向性尖锐程度及分辨性能都要低于CRR-CS算法；CS-OMP算法分辨两个声源的能力较差．同时在图中可以发现随着信噪比的下降,各算法对于多声源的分辨能力也在下降,但CRR-CS算法仍明显优于其他算法．

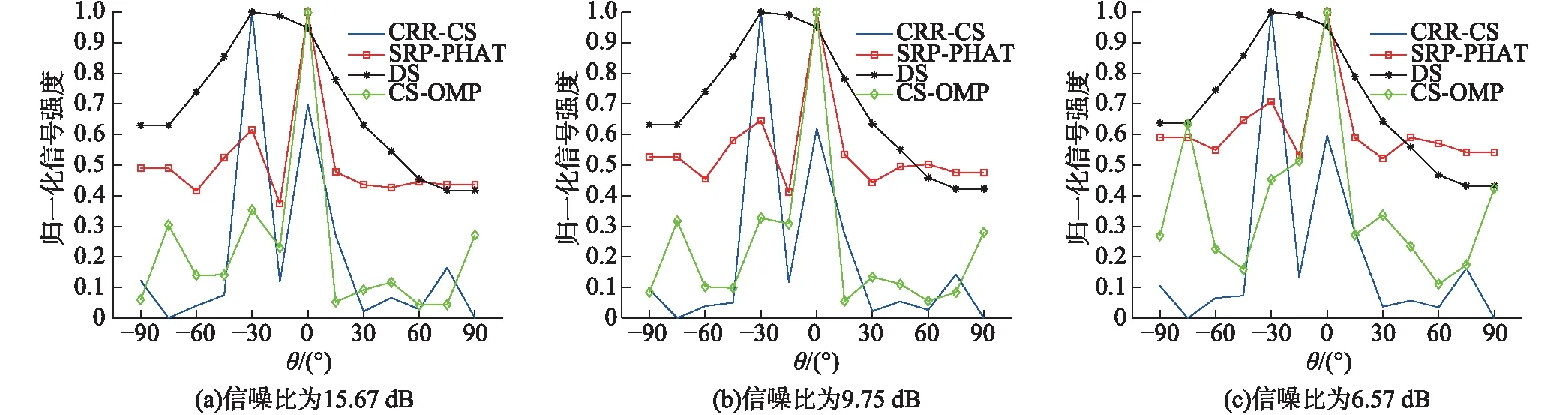
图1　不同信噪比下各算法对多声源的分辨性能Fig.1 Resolving performance of multiple sources for each algorithm at different signal noise ratios

考虑到实验设置的分辨率为15°,故采用样条插值法进行均方根误差(RMSE,εRMSE)性能评估[16]．各算法信号强度最高的两处分别通过样条插值法获得预测角度,真值方向为声源所在的角度，通过式(16)计算各算法的RMSE,考虑到DS算法无法分辨出2个不同的声源,故不参与比较．

图2　不同频点阈值下各算法对多声源的分辨性能Fig.2 Resolving performance of multiple sources for each algorithm at different frequency threshold

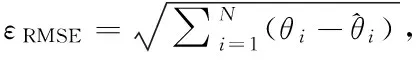
(16)

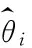
从表2可以看出各算法随着信噪比的下降,RMSE总体上有增加的趋势,但CRR-CS的结果不但误差较小,且增长小于其余两种算法,而CS-OMP算法在6.57 dB信噪比环境下的预测角度出现了明显的错误．

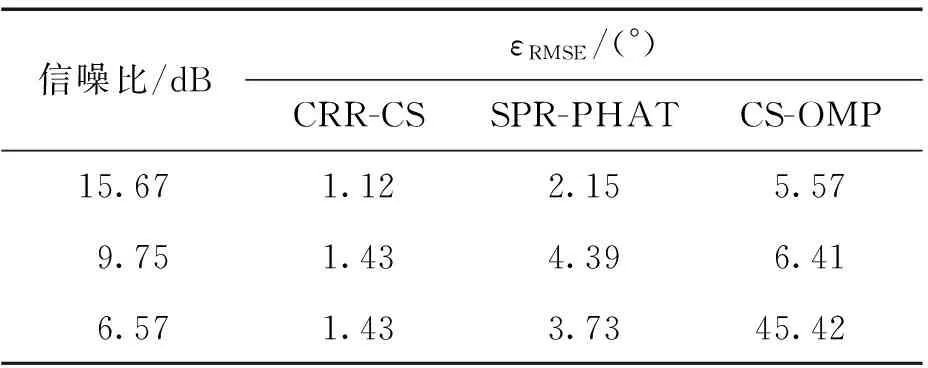
表2　不同信噪比下各算法DOA估计的RMSE

2.2.2不同频点阈值下各算法对多声源的分辨性能

当I=2,信噪比为15.67 dB时,不同算法频点阈值条件下各算法对多声源的分辨能力如图2所示.

由于DS算法与SRP-PHAT算法中无需设置频点阈值，故此部分没有参数发生变化,故DS算法与SRP-PHAT算法的结果在此处仅作参考．从图2中可以看出随着频点阈值η的增大,CS-OMP算法与CRR-CS算法的分辨能力都有所提升,但CRR-CS算法性能要明显优于CS-OMP算法．

2.2.3不同稀疏度下各算法对多声源的分辨性能

当信噪比为15.67 dB,η=0.15时,不同声源数I条件下各算法对多声源的分辨能力如图3所示.

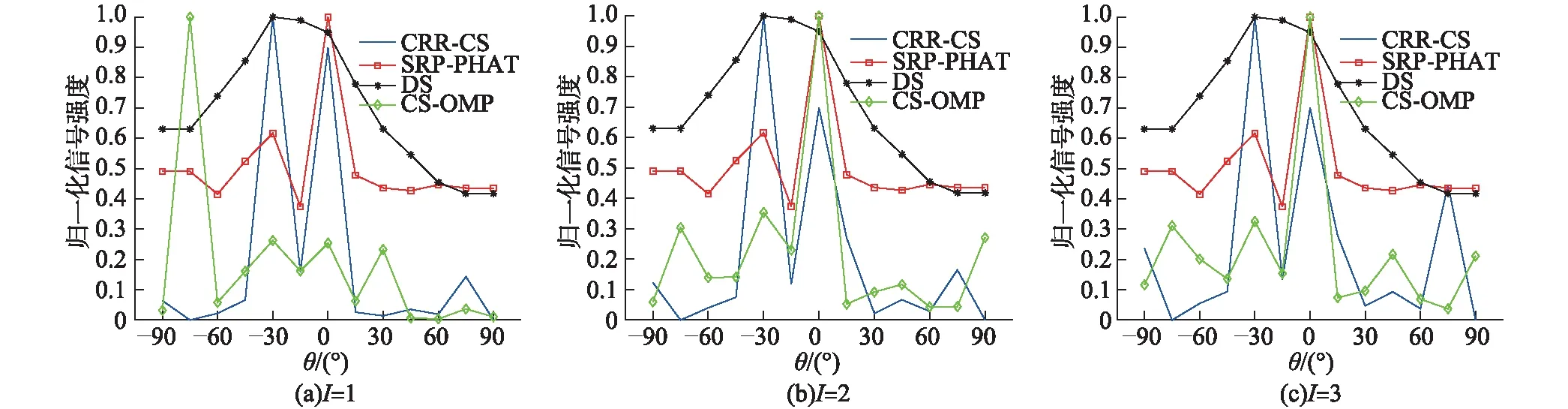
图3　不同稀疏度下各算法对多声源的分辨性能Fig.3 Resolving performance of multiple sources for each algorithm at different sparseness

考虑到实际应用场景中往往无法准确获知声源准确数量,文中对设置不同声源数时传统OMP算法与CRR-CS算法的性能变化信息评估．在实验中分别设I为1,2,3,对比CS-OMP和CRR-CS算法在不同稀疏度下的分辨性能．I=1时,CS-OMP算法无法成功定位出声源位置且不能分辨多声源，I为2和3时能够定位准确但分辨效果差；尽管CRR-CS算法随着稀疏度的增加分辨性能有所下降,但仍旧远优于CS-OMP算法．可见CRR-CS算法对于设置不同声源数的情况下,其估计结果仍具有一定的稳健性．

3　结　论

本研究将基于CS的麦克风阵列定位算法应用于多声源环境当中,在CS-OMP算法的基础上,考虑到多声源场景,通过利用阵元间时延关系直接产生的房间冲激响应进行混合矩阵构造．结果表明,本文中提出的CRR-CS算法对多声源的方位估计能力相比SRP-PHAT和DS算法更优秀,且在不同信噪比环境中均对多声源有更好的分辨能力．同时,在声源数未知及不同频点阈值的情况下,CRR-CS算法的分辨及定位性能要比CS-OMP算法强．可见:文中利用麦克风阵列阵元之间的时延关系构造房间冲激响应既减少了需要进行实测的房间冲激响应的步骤,又提高了多声源分辨能力．

参考文献：

[1]WAX M,KAILATH T.Optimum localization of multiple sources by passive arrays[J].IEEE Transaction on Acoustics，Speech,and Signal Processing,1983,31(5):1210-1217.

[2]GUSTAFSSON T,RAO B D,TRIVEDI M.Source localization in reverberant environments:modeling and statistical analysis[J].IEEE Transactions on Speech and Audio Processing,2003,11(6):791-803.

[3]HUANG L,WU S J,ZHANG L R.A novel MUSIC algorithm for direction-of-arrival estimation without the estimate of covariance matrix and its eigendecomposition[C]∥Proceedings of IEEE International Conference on Vehicular Technology.Stockholm:IEEE,2005:16-19.

[4]ZHAO X Y,TANG J,ZHOU L,et al.Accelerated steered response power method for sound source localization via clustering search[J].Science China Physics,Mechanics and Astronomy,2013,56(7):1329-1338.

[5]张艳娜.基于麦克风阵列的多声源定位算法研究[D].沈阳:沈阳航空航天大学,2014:11-15

[6]付金山,李秀坤.声矢量阵 DOA 估计的稀疏分解理论研究[J].哈尔滨工程大学学报,2013,34(3):281-286.

[7]伍飞云,童峰.块稀疏水声信道的改进压缩感知估计[J].声学学报,2017,42(1):27-36.

[8]金光明.基于麦克风阵列多声源定位的新方法[J].东北大学学报(自然科学版),2012,33(6):769-773.

[9]赵小燕,周琳,吴镇扬.基于压缩感知的麦克风阵列声源定位算法[J].东南大学学报(自然科学版),2015,45(2):203-207.

[10]李剑汶,章宇栋,童峰.一种采用旁瓣增强的麦克风阵列抗混响算法[J].厦门大学学报(自然科学版),2017,56(5):711-717.

[11]CANTLES E,ROMBERG J.Uncertainty principles:exact signal reconstruction from highly incomplete frequency information [J].IEEE Transactions on Information Theory,2006,52(2):489-509.

[12]TROPP J A,GILBERT A C.Signal recovery from random measurements via orthogonal matching pursuit[J].IEEE Transactions on Information Theory,2007,53(12):4655-4666.

[13]李芳兰,周跃海,童峰.采用可调波束形成器的GSC麦克风阵列语音增强方法[J].厦门大学学报(自然科学版),2013,52(2):186-189.

[14]GAROFOLO J S,LAMEL L F,FISHER W M,et al.TIMIT acoustic-phonetic continuous speech corpus LDC93S1.[DB/OL].[2017-06-22].https:∥catalog.ldc.upenn.edu/LDC93S1.

[15]BENESTY J,CHEN J,HUANG Y.Microphone array signal processing[M].Berlin Heidelberg:Springer Science & Business Media,2008:43-46.

[16]GANGNLY A,REDDY C,HAO Y,et al.Improving sound localization for hearing aid devices using smartphone assisted technology[C]∥2016 IEEE International Workshop on Signal Processing Systems (SiPS).Dallas:IEEE,2016:165-170.