辐照条件下Zr-Nb二元合金的相图计算

王翠萍,李林阳,卢　勇,郭毅慧,刘兴军

(厦门大学材料学院,福建 厦门 361005)

在核反应堆中,核燃料芯块外面的包壳作为核燃料的保护层[1],受到强烈的辐照、高温、高压以及腐蚀等作用[2-3],对核反应堆的正常运行具有非常重要的影响．Zr合金因具有高温下强度高,中子吸收截面小和加工性能较好等优点[4],已被广泛地用作反应堆的包壳材料[1-5]．Nb是Zr基包壳材料的重要添加元素,其热中子吸收截面小,能削弱碳、氮、铝等杂质对合金抗腐蚀性能和力学性能的有害作用,强化Zr合金的同时降低Zr合金的吸氢量[6-7],因此Zr-Nb合金是一种重要的包壳材料．

包壳材料在核反应堆中使用时必然会受到离子、中子或电子等辐照的影响,而由能量粒子引起的辐照效应不仅能在一定程度上加速相变的进行,还可能改变相的稳定性[8]．Turkin等[9]应用一个描述辐照下相位稳定性改变的模型,利用相干和非相干析出物的稳定性标准差,研究了在不同辐照条件下Zr-Nb相图中富Zr侧的变化，结果表明,在辐照条件下,共析反应(βZr) ↔ (Nb)+(αZr)的反应温度会降低．这个结果无法用传统的热力学平衡相图[10]来加以解释．因此,研究辐照条件下Zr-Nb二元合金的相图是十分必要的．

本研究基于文献报道的Zr-Nb二元合金的扩散参数和已优化的热力学参数,应用热力学模型和辐照条件下的有效自由能模型,讨论不同辐照条件对体系中缺陷浓度、自扩散系数和有效自由能的影响,计算在不同辐照条件下Zr-Nb二元合金的稳态相图,并与热力学平衡相图进行详细的比较．

1　有效自由能模型

1.1　模型介绍

Martin[11]基于Cahn-Hilliard[12]扩散方程,从扩散平衡的角度提出了一个在辐照条件下更合理的有效自由能模型．在该有效自由能模型中,将相互扩散通量看成是弹道通量和由化学势梯度驱动的扩散通量的总和．在A-B二元系统中,原子的扩散通量可以有以下两个表达式[11]:

J=-Mc=

(1)

(2)

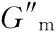
(3)

摩尔吉布斯自由能Gm可以通过亚正规溶体近似求得,表达式如下:

(4)

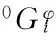
LA,B=a1+a2T+a3TlnT,

(5)

(6)

原子迁移率M可以通过下式[11]求得:

(7)

ωb=ηreplK0.

(8)

其中:ηrepl为每次原子离位引起的原子置换数,取值范围为1～1 000 dpa-1(dpa表示每个晶格原子的平均离位次数)[14];K0为原子的离位率,即一个原子每秒钟发生的离位数,取值范围通常为10-7～10-2dpa/s[15]．在本研究中,辐照的强度是通过ηrepl和K0来体现的,当辐照强度增大时,ηrepl和K0也随之增大．

为了求出弹道自由能K,Ravishankar等[16]根据化学式的定义引入了弹道势,再通过Gibbs-Duhem关系,将式 (6) 中的二次导数转化成两个一次导数的加和,即将二次积分的求解转变成通过一次积分来进行求解:

(9)

本研究中假设Db、DA及DB不受浓度的影响,再取边界条件K(0)=0,K(1)=0,然后通过积分得到弹道自由能K的表达式为

(10)

最终得到有效自由能Φ的表达式[11]为

Φ=Gm+K.

(11)

1.2　辐照条件下扩散系数的计算方法

溶质原子的扩散机制一般有交换机制、空位机制、间隙机制、表面扩散机制和晶界扩散机制[14],在本研究中考虑空位机制与间隙机制．因此,A原子的自扩散系数可以由下式表示:

(12)

(13)

(14)

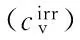
(15)

(16)

其中：K0为原子离位率,Kis为间隙原子-势阱之间的反应系数,Kiv为间隙原子-空位之间的反应系数,Kvs为空位-势阱之间的反应系数；cs为势阱浓度,可通过ρd=4πrvscs求得,ρd是体系中的位错密度,在本研究中取值为1010～1016m-2[18]．Kis、Kiv和Kvs可由下式[14]求得：

表1　本研究中所使用的扩散参数

Tab.1　Diffusion data used in this study

相原子Evf/eVEif/eVEvm/eVEim/eVriv[17]/nmrvs[17]/nmris[17]/nm(βZr)Nb2.75[19]—1.21[19]0.15[19]0.690.300.30Zr0.36[23]4.032[25]0.73[23]0.55[20]0.740.300.30(αZr)Nb2.00[24]—0.26[24]0.15[19]0.690.300.30Zr1.80[21]2.89[23]1.62[22]0.55[20]0.740.300.30(Nb)Nb2.75[19]—1.21[19]0.15[19]0.690.300.30Zr0.36[23]4.032[25]0.73[23]0.55[20]0.740.300.30

图1　(αZr)相和(βZr,Nb)相中空位的平衡浓度在不同原子离位率与位错密度下随温度的变化Fig.1 Vacancy equilibrium concentrations of (αZr) phase and (βZr,Nb) phase as a function of temperature for various combinations of displacement rates and dislocation densities

(17)

其中,ris为间隙原子-势阱之间的相互作用半径,riv为间隙原子-空位之间的相互作用半径,rvs为空位-势阱之间的相互作用半径．

因此,在辐照条件下体系中的空位和间隙原子的平衡浓度分别等于热平衡浓度与过剩浓度之和,即:

(18)

(19)

因为在辐照诱导下会产生点缺陷,所以辐照条件下A原子的自扩散系数的表达式[14]为

(20)

同样地,辐照条件下B原子的自扩散系数DB也可以用相似的表达式来表示．然后将DA和DB代入式(10)和(11) 中便可获得体系中各相的有效自由能．

2　结果与讨论

2.1　辐照条件下有效自由能的计算

计算Zr-Nb二元合金在辐照条件下的稳态相图,首先要对不同辐照条件下的有效自由能进行研究．根据式 (10) 和 (20) 可知,有效自由能主要受到体系中扩散系数D、位错密度ρd、原子离位率K0、原子置换数ηrepl、原子浓度c和温度T的影响．

本研究所采用的热力学参数基于Fernandez优化的结果[10],相关的扩散参数[17,19-25]如表1所示．在此基础上,分别计算了辐照条件下(αZr) 相和(βZr,Nb)相中的空位平衡浓度随原子离位率与位错密度的变化情况,如图1所示：辐照条件下的空位平衡浓度均比其热平衡浓度大,二者在低温下差异明显,而高温下则趋于一致;且随着原子离位率的增大和位错密度的减小,空位平衡浓度增大．

图2是计算的在辐照条件下(αZr)相和(βZr,Nb)相中Nb原子的自扩散系数随原子离位率与位错密度的变化情况,其中实线表示Nb原子在无辐照下的自扩散系数 (Dth),虚线则表示在不同辐照条件下的自扩散系数．可以看出,在辐照条件下,Nb原子的自扩散系数具有与空位平衡浓度相似的变化规律,即:辐照条件下Nb原子的自扩散系数均比无辐照下的大,二者在低温下差异明显,而高温下则趋于一致;且随着原子离位率的增大和位错密度的减小,Nb原子的自扩散系数也增大．

图2　(αZr)相和(βZr,Nb)相中Nb原子的自扩散系数在不同原子离位率与位错密度下随温度的变化Fig.2 Self-diffusion coefficients of atoms Nb in the (αZr) phase and (βZr,Nb) phase as a function of temperature at a series of displacement rates and dislocation densities

这是由于在高温条件下,缺陷的热平衡浓度较高,辐照诱导形成的缺陷浓度相比之下非常小,所以辐照对空位平衡浓度和Nb原子的自扩散系数在高温下的贡献较小;而低温条件下的热扩散相当缓慢,缺陷的热平衡浓度很低,辐照使得体系中的缺陷浓度明显增大,并逐渐超过空位的热平衡浓度而占据主导地位,导致体系中的扩散加速．当原子离位率增大和位错密度减小时,级联碰撞过程更剧烈,辐照诱导的过剩空位浓度随之增加,从而提高了体系的空位平衡浓度,促进了体系的扩散．

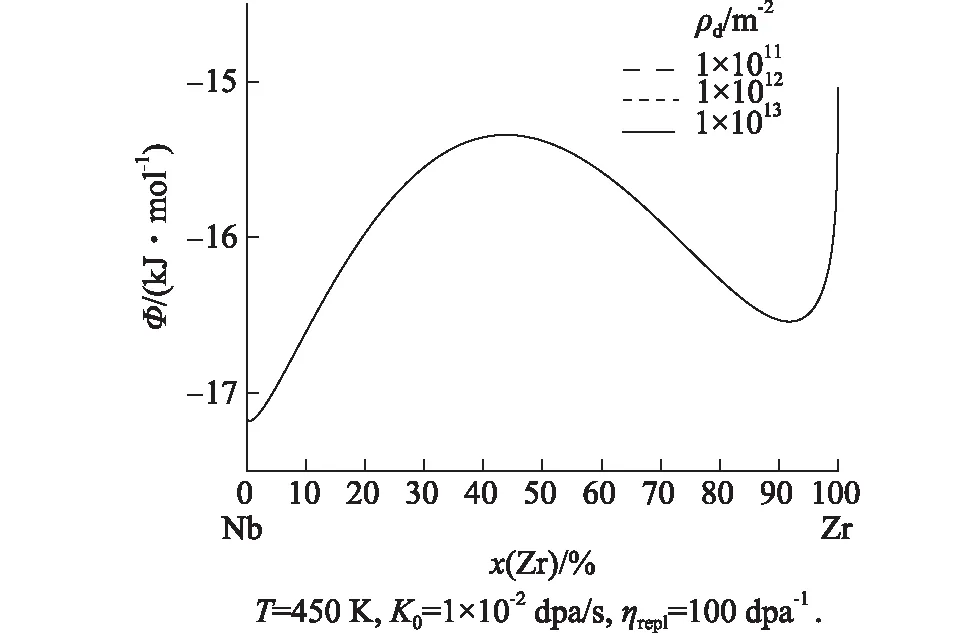
图3　不同位错密度下(βZr,Nb)相的有效自由能Fig.3 Effective free energy of the (βZr,Nb) phase with different dislocation densities

图3是在450 K,K0=1×10-2dpa/s,ηrepl=100 dpa-1的条件下,计算的不同位错密度对(βZr,Nb)相的有效自由能的影响．可以看出,在辐照条件下位错密度对(βZr,Nb) 相的有效自由能影响很小，基本不变,这是由于体系中的位错处于强重组机制,并且缺陷重组足以超过缺陷湮没的作用,即相比于在势阱处湮没,缺陷更倾向于相互复合．这可以通过在Sizmann′s方程[17]中比较缺陷重组与缺陷湮灭的分数来得到证明．因此本研究为了简便计算,将位错密度ρd设为定值3×1013m-2．

图4(a)～(c)是计算的(βZr,Nb) 相的有效自由能随温度、原子离位率和原子置换数的变化情况．由图可知：与无辐照条件相比，(βZr,Nb)相的有效自由能在辐照条件下会出现降低的现象,随着原子离位率和原子置换数的增大,有效自由能降低,这是由于在辐照条件下存在弹道自由能K,K会随着原子离位率和原子置换数的增大而增大,导致有效自由能的降低;低温下(βZr,Nb) 相的有效自由能的降低幅度比高温下的大,说明在低温条件下辐照对有效自由能的影响比在高温条件下更为显著．

(a)中实线为无辐照条件下，虚线为辐照条件下，K0=1×10-2 dpa/s.图4　计算的(βZr,Nb)相的有效自由能随温度(a)、原子离位率(b)和原子置换数(c)的变化Fig.4 Calculated effective free energy of the (βZr,Nb) phase with different temperatures(a),displacement rates(b) and atomic displacement numbers (c)

2.2　辐照条件下的相图计算

根据最小自由能原理和公切线法则,计算了(βZr,Nb) 相在不同原子离位率下的溶解度间隙(图5)，并比较了Zr-Nb二元合金在不同辐照条件下的稳态相图(图6)．

从图5中可以看出：在辐照条件下,高温部分(βZr,Nb) 相的溶解度间隙并未出现明显变化,即(βZr,Nb)↔(βZr)+(Nb);而在低温部分,溶解度间隙从开口状逐渐转变成一个完全闭合的区域，且随着原子离位率的增大,闭合区域的低温临界温度越高,这个两相分离的闭合区域越小．从图6可以看出：在高温部分辐照条件下的稳态相图与热力学平衡相图基本一致；但在低温部分两者却出现明显的区别，在辐照条件下,稳态相图的低温区域出现了连续固溶的(βZr,Nb) 相,从而出现了一个低温包析反应(αZr)+(Nb)↔(βZr,Nb)．

图5　不同原子离位率下(βZr,Nb)相的溶解度间隙Fig.5 Miscibility gap of the (βZr,Nb) phase under different displacement rates

计算得到的Zr-Nb二元合金中的不变系反应结果如表2所示:在辐照条件下,共析反应(βZr) ↔ (Nb)+(αZr)的温度出现小幅度的降低,这与Turkin等[9]的计算结果一致;此外,在辐照条件下,Zr-Nb二元合金的稳态相图中出现了一个低温包析反应和两相分离反应,当原子离位率和原子置换数增大时,即当辐照强度增大时,低温包析反应的温度会随之升高,(βZr,Nb)相的相区也随之增大,这与前文中在低温条件下辐照对有效自由能的影响比在高温条件下更为显著的结论相印证．

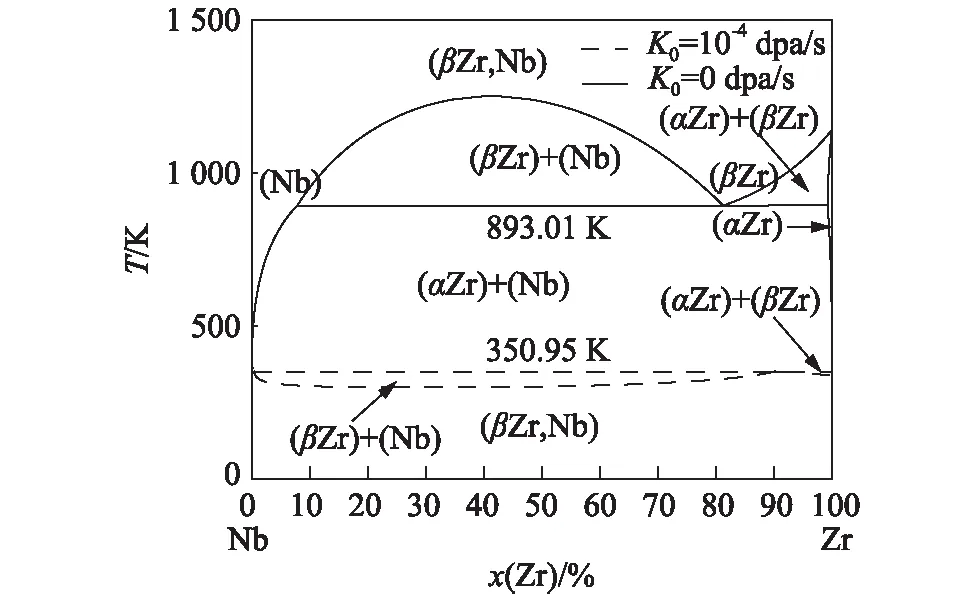
图6　Zr-Nb二元合金的热力学平衡相图与辐照条件(K0=10-4dpa/s,ηrepl=100 dpa-1)下稳态相图的比较Fig.6 Comparison between the thermodynamic equilibrium phase diagram and the steady-state phase diagram of the Zr-Nb binary alloy under K0=10-4dpa/s and ηrepl=100 dpa-1

表2　Zr-Nb二元合金中的不变系反应

Tab.2　The invariant reactions in the Zr-Nb binary alloy

反应类型x(Zr)/%(βZr)(Nb)(αZr)(βZr,Nb)T/KK0/(dpa·s-1)ηrepl/dpa-1共析反应81.297.89[10]99.28[10]893.01[10]0 (βZr)↔(Nb)+(αZr)81.287.8999.26892.851×10-410081.257.8999.23892.591×10-310081.197.8999.14892.111×10-210081.277.8999.27892.811×10-210包析反应4.0799.9990.13350.951×10-4100(Nb)+(αZr)↔(βZr,Nb)6.1399.9989.44387.861×10-31008.9899.9988.71429.321×10-21004.2399.9990.10352.581×10-210高温临界点41.32[10]1250[10]0 (βZr,Nb)↔(βZr)+(Nb)41.311250.021×10-410041.301250.051×10-310041.281250.101×10-210041.311250.031×10-210低温临界点25.34299.851×10-4100(βZr,Nb)↔(βZr)+(Nb)25.04327.851×10-310029.72364.771×10-210029.33298.311×10-210

3　结　论

本研究应用热力学模型和辐照条件下的有效自由能模型,对包壳材料Zr-Nb二元合金在辐照条件下的稳态相图进行了计算,研究了不同辐照强度对其稳态相图的影响．结果表明:在辐照条件下,Zr-Nb合金稳态相图的高温部分与热力学平衡相图基本一致,在低温区域则出现了连续固溶的(βZr,Nb) 相,从而出现了一个低温包析反应(Nb)+(αZr)↔(βZr,Nb),且随着辐照强度的增大,低温包析反应的温度升高,(βZr,Nb)相的相区也随之增大，即由于辐照的作用,原本在高温时稳定存在的(βZr,Nb)相也能在低温时稳定存在．该研究结果可为包壳材料的合金设计提供理论基础．

参考文献：

[1]赵文金.核工业用高性能锆合金的研究[J].稀有金属快报,2004(5):15-20.

[2]崔超,黄晨,苏喜平,等.快堆先进包壳材料 ODS 合金发展研究[J].核科学与工程,2011,31(4):305-309.

[3]VRTILKOVA V,VALACH M,MOLIN L.Oxiding and hydriding properties of Zr-lNb cladding material in comparison with zircaloys[C].Vienna:[s.n],1997:227-251.

[4]罗上庚.研究堆铝包壳元件水池贮存的腐蚀问题[J].核科学与工程,1999,19(1):80-84.

[5]周邦新.改善锆合金耐腐蚀性能的概述[J].金属热处理学报,1997,18(3):8-15.

[6]YAN Y,BURTSEVA T A,BILLONE M C.High-temperature steam-oxidation behavior of Zr-1Nb cladding alloy E110[J].Journal of Nuclear Materials,2009,393(3):433-448.

[7]NEOGY S,SRIVASTAVA D,TEWARI R,et al.Microstructural study of hydride formation in Zr-1Nb alloy[J].Journal of Nuclear Materials,2003,322(2):195-203.

[8]RIVIERE J P,DINHUT J F.Disordering kinetics in neutron and electron irradiated Fe-Co alloy[J].Scripta Metallurgica,1983,17(7):885-888.

[9]TURKIN A A,BUTS A V,BAKAI A S.Construction of radiation-modified phase diagrams under cascade-producing irradiation:application to Zr-Nb alloy[J].Journal of Nuclear Materials,2002,305(2):134-152.

[10]GUILLERMET A F.Thermodynamic analysis of stable phases in the Zr-Nb system and calculation of the phase diagram[J].Zeitschrift für Metallkunde,1991,82(6):478-487.

[11]MARTIN G.Phase stability under irradiation:ballistic effects[J].Physical Review B,1984,30(3):1424-1436.

[12]CAHN J W,HILLIARD J E.Free energy of a nonuniform system.Ⅰ.Interfacial free energy[J].The Journal of Chemical Physics,1958,28(2):258-267.

[13]DINSDALE A T.SGTE data for pure elements[J].CALPHAD,1991,15(4):317-425.

[14]WAS G S.Fundamentals of radiation materials science:metals and alloys[M].Michigan:Springer Science & Business Media,2007:191-193.

[15]RUSSELL K C.Phase stability under irradiation[J].Progress in Materials Science,1984,28(3/4):229-434.

[16]RAVISHANKAR N,ABINANDANAN T A,CHATTOPADHYAY K.Application of effective potential formalism to mechanical alloying in Ag-Cu and Cu-Fe systems[J].Materials Science and Engineering:A,2001,304:413-417.

[17]SIZMANN R.The effect of radiation upon diffusion in metals[J].Journal of Nuclear Materials,1978,69:386-412.

[18]胡赓祥,蔡珣,戎咏华.材料科学基础[M].上海:上海交通大学出版社,2000:108.

[19]LIU X J,ZHAO Y L,LU Y,et al.Steady-state dynamical phase diagram calculation of U-Nb binary system under irradiation:ballistic effect[J].Journal of Nuclear Materials,2014,451(1):366-371.

[20]HUANG G Y,WIRTH B D.First-principles study of diffusion of interstitial and vacancy inαU-Zr[J].Journal of Physics:Condensed Matter,2011,23(20):205402.

[21]MONTI A M.Diffusion constants for the vacancy mechanism in Mg andα-Zr calculation[J].Physica Status Solidi (b),1991,167(1):37-49.

[22]HOOD G M.Diffusion and vacancy properties ofα-Zr[J].Journal of Nuclear Materials,1986,139(3):179-184.

[23]XIN X K,LAI W S,LIU B X.Point defect properties in hcp and bcc Zr with trace solute Nb revealed byabinitiocalculations[J].Journal of Nuclear Materials,2009,393(1):197-202.

[24]KORZHAVYI P A,ABRIKOSOV I A,JOHANSSON B,et al.First-principles calculations of the vacancy formation energy in transition and noble metals[J].Physical Review B,1999,59(18):11693-11703.

[25]BEELER B,GOOD B,RASHKEEV S,et al.First principles calculations for defects in U[J].Journal of Physics:Condensed Matter,2010,22(50):505703.