基于绕射理论的大尺度桥墩波浪力计算方法

邓莎莎,沈火明,刘　浪,唐怀平

(1.西南交通大学力学与工程学院,四川 成都 610031; 2.四川省交通厅公路规划勘察设计研究院,四川 成都 610041)

跨海桥梁下部结构多属大尺度结构，必须考虑波浪的绕射效应,对于圆形桥墩绕射效应的计算可参考《海港水文规范JTS 145-2—2013》中的方法进行估算[1].对于小尺度墩柱,该规范采用Morison方程计算波浪力;对于大尺度圆形墩柱,该规范给出了建立在绕射理论上的圆形墩柱一次近似解的结果,而对方形墩柱,只给出了经验计算方法或等效为圆形墩柱的计算方法.在桥梁基础结构设计阶段,通常采用物理模型试验来确定桥梁基础所受的波浪力,如已建或在建的杭州湾跨海大桥、舟山连岛金塘大桥、东海大桥、港珠澳大桥等[2].但此方法存在一定的缺陷：一方面物理试验通常采用缩尺比模型[3],不能模拟真实情况下波浪对大尺度结构的作用；另一方面由于造波、造流技术有限,不能还原真实海洋环境中的波浪情况[4].对于大尺度结构波浪力的理论计算,国内外主要有以下两种方法:(1) 目前来说应用最为广泛的绕射理论,由MacCamy和Fuchs于1954年提出[5-6],即通过对结构物边界上的入射波和绕射波速度势叠加来得到总的速度势,但此法仅对圆柱有效,而不适于其他截面形式的结构[7-8]；(2) Froude-Krylov假定波浪原有的压强分布不因结构物的存在而改变[9],先算出未扰动的入射波在结构物边界上的作用力,再乘以反映附加质量效应和绕射效应的系数进行修正,但此绕射系数需要通过模型试验加以确定.数值计算方法的研究主要包括:滕斌采用高阶边界元法对海洋结构所受的波浪力进行了数值模拟[10-11];祝兵和康啊真等对波浪与大尺度桥梁围堰结构相互作用问题进行了三维数值模拟[12];田宏升对作用于大尺度结构物上的波浪力计算方法做出了总结[13].综上可见,基于绕流波浪理论,针对大尺度桥墩波浪力的研究还不多.国内的研究大多是应用已有的绕射波浪理论计算承台和桥墩受到的波浪力,鲜有文献开展针对计算方法本身进行修正、拓展或创新的研究.因此,本文基于绕射理论对大尺度桥墩波浪力的计算方法进行研究具有一定的实际意义.

1　绕射理论

绕射是指入射波的波浪场与置于其中的相对静止的结构之间的相互作用.在存在大尺度结构时,必须考虑入射波的绕射效应以及自由表面效应,此时波浪对结构的作用主要包括附加质量效应和绕射效应,黏滞效应相比之下影响较小,可忽略不计.

假定入射波为线性的,且波浪与结构的相互作用也是线性的,则波浪力对大尺度结构作用如图1所示，图中，a为图形截面半径.采用MacCamy和Fuchs所提的绕射理论推导如下[7].

假定入射波ΦI为线性波,且沿x正向传播,波速为c,将入射波速度势表示为贝塞尔函数的级数，即

(1)

式中:g为重力加速度;

H为两倍的波高;

r为半径;

d为水深;

ω=2π/T为圆频率;

k=2π/L为波数;

t为时间；

i为虚数,满足 i2=-1.

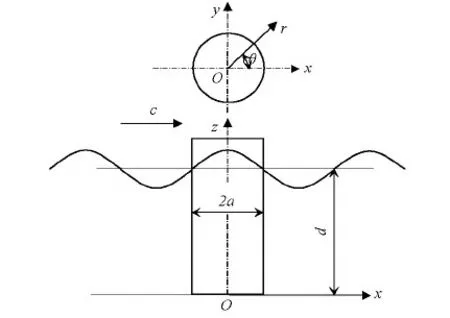
图1　大直径圆柱波浪力计算坐标系统Fig.1　Coordinate system of calculating wave forces acting on large diameter cylinder (c is wave speed)

直立圆柱体绕射势φD如(2)所示.

(2)

代入自由表面动力边界条件、水底边界条件、柱面边界条件(入射波反射波速度势相等方向相反)、无限远处辐射边界条件,则绕射波ΦD解的形式可类似式(1)变为式(3).

(3)

式中:Hm(kr)为第一类Hankle函数;

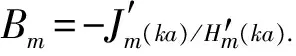
将绕射势和入射势代入柱面边界条件可得总速度势为

φ=φI+φD=

(4)

按绕射理论推导的大尺度圆形桥墩惯性力系数CM直接反映了波浪力大小,如式(5)所示.

(5)

由以上推导可知MacCamy绕射理论仅适用圆形截面桥墩,同时理论有待完善,计算后的缺陷体现在以下几个方面:(1) 若严格参照理论推导,绕射势ФD并非式(3)所表达的形式,此处类比了式(1)的解；(2) 假定线性波波长为4m,当圆柱直径为4m时,根据此理论推导出的CM=0.25,而当直径缩小到1m时,CM=1.85.根据这两个CM值计算得到的波浪力相差2倍多,而通过数值计算得到的波浪力相差8倍左右,一定程度上可反应绕射理论计算CM曲线在精度上存在误差；(3) 现存规范，如：日本规范《港湾设计技术标准及编制说明》、美国规范《海上移动钻井平台建造和入级规范》、挪威规范《环境条件和环境荷载规范》、英国标准BS6349《海工建筑物》、德国《劳式规范和准则》等都提到了采用绕射理论计算大尺度墩柱结构波浪力,但均为原则性上的建议,这也说明绕射理论不够完善[14-15].

2　流固耦合计算模型

绕射效应显著程度由截面形状和截面尺度控制,其系数应由物理模型试验确定.但由于造波精度要求及模型尺寸过大,进行足尺试验十分困难.因此,本文拟通过数值模拟的方法来确定波浪的绕射系数,以节约成本及提高计算速度.

通常,流固耦合分为单向流固耦合和双向流固耦合.在实际海洋环境中,流体与桥梁下部结构是相互作用相互影响的.在地震或者较强波流的作用下,桥梁的下部结构会产生较大的变形,同时下部结构的变形反过来会对流场域产生干扰,从而改变流场域的流体参数.因此对跨海桥梁下部结构应采用双向流固耦合的方法进行模拟[16-17].

基于此,本文采用ANSYS-CFX软件进行分析,该软件在计算时会考虑两者之间的相互影响,最终达到一个平衡状态[18].

设波浪波长为L,圆形桥墩直径为D,由Morison方程适用条件可知:当D/L<0.2时属于小尺度结构;当D/L>0.2时属于大尺度结构.

本文选取线性波为入射波,L=6 m,H=0.2 m,波高与波长相比数值较小,可认为该波是微幅波.设置计算域水深为5 m.则由适用条件可知当D=1.2 m时为大尺度结构和小尺度结构的分界点.当D=0.5 m,2 m时,分别对应小尺度和大尺度,其在波浪作用下的流线图如图2所示,两尺度流线图差异不大.当波浪到达圆形桥墩时,由于桥墩阻拦,波浪运动方向改变,将绕桥墩通过,因此桥墩两侧会出现较大的流速.当方形桥墩边长为0.5 m 和2 m时,分别对应小尺度和大尺度,其在波浪作用下的流线图如图3所示,两尺度流线图差异较大.由图3可知:小尺度方形桥墩在波浪作用下的流线图与圆形桥墩相似,波浪绕桥墩通过;大尺度方形桥墩会在迎水面出现水流速度峰值,此时波浪无法顺利绕桥墩通过,而是产生了绕射,新形成的绕射波又与入射波叠加,从而形成了新的波浪场,此时结构受到的波浪力与小尺度结构相对会发生较大的变化,因此在计算大尺度结构时必须考虑绕射效应.

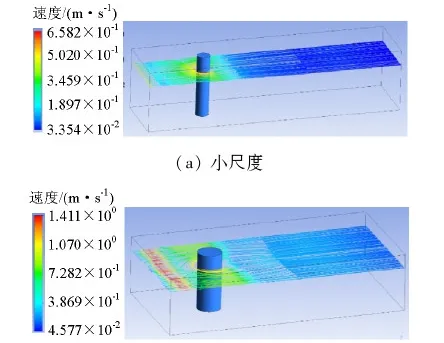
(b) 大尺度图2　不同尺度圆形桥墩流线图Fig.2　Streamline charts of circular piers at different scales

(b) 大尺度图3　不同尺度方形桥墩流线图Fig.3　Streamline charts of square piers at different scales

3　结果与分析

分别建立直径(边长)D=0.5,1.0,1.5,2.0,2.5,3.0,3.5,4.0 m的圆形(方形)桥墩模型,同时适当加宽数值波浪水槽宽度.设定H=0.5 m,计算各工况在波浪作用下的波浪力,可得工况液面图,部分如图4、5所示.图中，左侧数值表示体积分数,等于1说明是液体,等于0说明是气体,因此图中液面为显示红色.

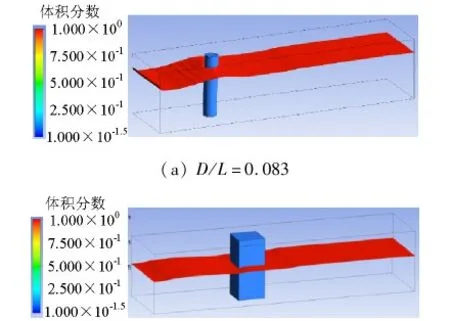
(b) D/L=0.333图4　不同尺度下圆形桥墩波浪作用液面图Fig.4　Liquid surface figure of circular piers at different scales

将求得的波浪力代入Morison方程可得到CM为

(6)

式中:fI为惯性力;ρ为液体密度;V0为排水体积;ux为墩柱沿x方向的位移;dux/dt为x方向的波速.

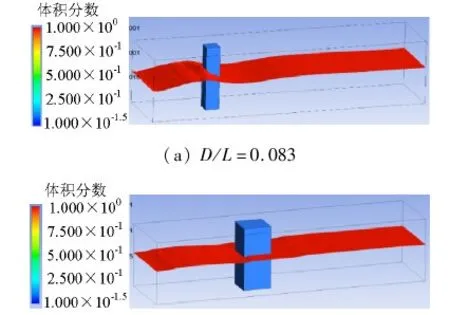
(b) D/L=0.333图5　不同尺度下方形桥墩波浪作用液面图Fig.5　Liquid surface figure of square piers at different scales

根据式(6)即可得不同直径圆形桥墩和不同边长方形桥墩的波浪力所对应的惯性力系数CM,值如表1所示.

表1　不同直径(边长)圆形(方形)桥墩CM值Tab.1　The values of circular pier and square pier at different scales

由表1可得惯性力系数CM与尺度关系曲线如图6所示.

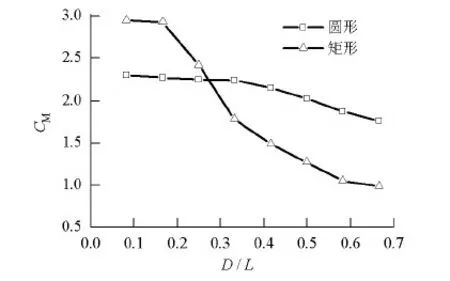
图6　惯性力系数与尺度关系曲线Fig.6　Relation curves of inertia coefficients and scales

由图6可知:当结构为小尺度且迎水宽度相同时,方形桥墩的CM值大于圆形桥墩,因此圆形桥墩更有利于波浪和水流的通过;当直径或边长与波长比值大于0.17时,方形桥墩和圆形桥墩都呈现出大尺度效应,即随着直径或边长的增大,CM值下降,且方形桥墩的CM值下降更明显,方形桥墩大尺效应更为显著.产生原因主要有两个:一是由于Morsion方程是由圆形桥墩推导,若方形桥墩直接套用公式会存在较大的误差;二是由于波浪的绕射效应,会在柱体表面形成散射波.虽然圆形桥墩表面入射波与散射波速度大小相等,但方向存在差异,而方形桥墩表面却会形成大小相等方向相反的绕射波,因此方形桥墩绕射效应更为明显.

由上可知,由于绕射效应的存在,Morison方程不能直接用于大尺度圆形桥墩上,可通过引入绕射系数对Morison方程进行修正后使用.修正后的Morison方程如式(7)所示.绕射系数与截面尺度关系如表2所示.

(7)

式中:FC为圆形桥墩所受波浪力;R为圆形桥墩绕射系数.

表2　圆形桥墩绕射系数与尺度关系Tab.2　Relationship between the diffraction coefficients and scales of circular pier

圆形桥墩的绕射系数为数值计算结果与原始Morison方程计算结果的比值,修正后的CM值呈直线分布，如图7所示.即小尺度和大尺度圆形桥墩都可通过Morison方程计算波浪力,只是大尺度需采用修正后的Morison方程.

图7　修正前后圆形桥墩对比Fig.7　Comparison of CM values of circular pier before and after correction

由上可知,Morison方程计算大尺度方形桥墩会存在较大的误差.这是由于方形桥墩所受波浪力的大小主要受横向尺度影响,与纵向尺度关系不大,但Morison方程计算时会将横向尺度与纵向尺度都纳入其中.因此若需使用Morison方程来计算大尺度方形桥墩,则必须对纵向尺度进行修正.本文将纵向尺度分别选为0.15L、0.20L、0.25L,对Morison方程进行修正,将此时所得波浪力与数值计算结果进行对比,可得关系曲线如图8所示.图中纵坐标表示方形桥墩所受沿x方向波浪力与重力G的比值,此处进行了无量纲化处理.由图8可知,当纵向尺度为0.2L与数值计算值更为吻合.

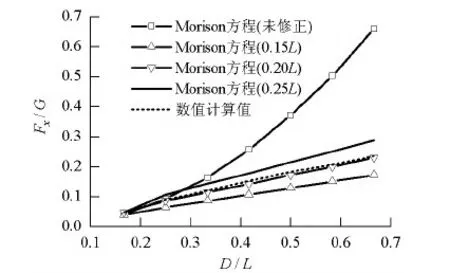
图8　波浪力与方形桥墩尺度关系曲线Fig.8　Relationship between wave forces and square piers

当纵向尺度取0.2L时,Morison方程(修正后)计算值与数值计算值的对比如表3所示.

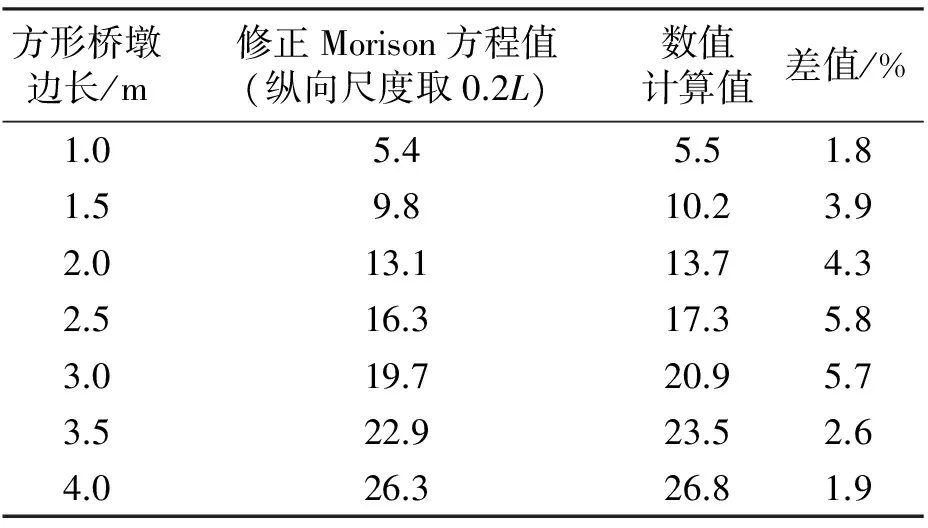
表3　Morison方程(修正后)与数值计算对比Tab.3　Comparison between Morison equation(corrected) calculation and numerical calculation

由表3可知,修正后的Morison方程能较好低与数值计算结果吻合,误差在10%以内.对于大尺度结构,纵向尺度取0.2L能简化计算过程,并有较好的精度.

4　结　论

通过数值模拟可确定波浪的绕射系数.当结构为小尺度且迎水宽度相同时,方形桥墩的CM值大于圆形桥墩;当为小尺度结构时,方形桥墩的CM值大于圆形桥墩;当为大尺度结构时,CM值随着直径或边长的增大而下降,且方形桥墩的CM值下降更明显,即方形桥墩大尺效应更为显著.

Morison方程引入绕射系数修正后能较好地计算大尺度圆形桥墩波浪力,纵向尺寸取0.2L能较好的计算方型桥墩波浪力.

参考文献:

[1]中华人民共和国交通运输部.JTS 145-2—2013 海港水文规范[S].北京:人民交通出版社,2013.

[2]兰雅梅,刘桦,皇甫熹,等.东海大桥桥梁桩柱承台水动力模型试验研究——第二部分:作用于群桩及承台上的波流力[J].水动力学研究与进展:A 辑,2005,20(3):332-339.

[3]郭超.桥墩冲刷与波流力的试验研究[D].北京:清华大学,2012.

[4]吴启和,牛照,田唯,等.港珠澳大桥埋置承台与桩波流作用动力响应分析与试验研究[J].中外公路,2014,34(1):121-124.

[5]邱大洪.波浪理论及其在工程中的应用[M].北京:高等教育出版社,1985:5-8.

[6]邱大洪,王永学.大直径圆柱体的非线性波浪力[J].海洋学报,1986,8(4):496-509.

[7]王树青,梁丙臣.海洋工程波浪力学[M].中国海洋大学出版社,2013:175-182.

[8]李世森,张伟,秦崇仁.大直径圆筒结构上波浪力的数值模拟与实验研究[J].中国港湾建设,2003,2(2):11-16.

LI Shisen,ZHANG Wei,QIN Chongren.Numerical simulation and experimental study of wave force on large diameter cylindrical structure[J].China Harbour Engineering,2003,2(2):11-16.

[9]FALTINSEN O M.Sea Loads on Ships and Offshore Structures[M].Cambridge University Press,1990:118-122

[10]李玉成,滕斌.波浪对海上建筑物的作用[M].海洋出版社,2002:278-284.

[11]滕斌.波浪力计算中的一个新边界元方法[J].水动力学研究与进展:A辑,1994(2):215-223.

[12]康啊真,祝兵,邢帆,等.超大型结构物受波浪力作用的数值模拟[J].工程力学,2014,31(8):108-115.

[13]田宏升.固定式海洋结构物荷载分析与研究[D].辽宁大连:大连理工大学,2005.

[14]Department of the Army Corps of Engineers.Coastal engineering manual[M].[S.l.]:US Army Corps of Engineers,2002:84-88.

[15]British Standard Institution.6349—12000 Maritime structures part 1:code of practice for general criteria[S].[S.l.]:Civil Engineering and Building Stuctures Sector Committee,2000.

[16]刘浪,杨万理,李乔.深水桥梁墩水耦合抗震分析方法[J].西南交通大学学报,2015,50(3):449-453.

LIU Lang,YANG Wanli,LI Qiao.Seismic analysis method of deep-water bridge pier and water coupling[J].Journal of Southwest Jiaotong University,2015,50(3):449-453.

[17]鲁丽,杨翊仁.流体和结构参数对板-流体耦合振动的影响[J].西南交通大学学报,2009,44(3):370-374.

LU Li,YANG Yiren.Influences of fluid and structural parameters on flow-induced vibrations of plate-fluid structure[J].Journal of Southwest Jiaotong University,2009,44(3):370-374.

[18]ANSYS I N C.CFX-Solver theory guide[M].Canonsburg:[s.n.],2009:112-127.