一种桩承式路堤沉降的简化计算方法

刘飞成,张建经,闫世杰

(西南交通大学土木工程学院,四川 成都 610031)

随着中国东部沿海地区的快速发展,高速铁路修建的需求也越来越大,而这一地区广泛分布着承载能力差、压缩性高的深厚软土,易引起高速铁路路堤的沉降超限,这也是各国的岩土工程师面临的一大难题.桩基础作为改良软土地基的一种有效手段[1-2]已经被广泛运用在软土地基的路堤修建中,并取得了良好的效果[3-4].

目前关于桩承式路堤的研究主要集中在承载能力分析[5-6]以及力的传递机制[7-8]上,对桩承式路堤的沉降研究相对较少.对一些软土地基路堤的设计而言,路堤沉降控制相比于地基承载能力更为重要[9-10].Abusharar等[5]认为目前尚没有被广泛认可的针对桩承式路堤的沉降计算方法,需要进行深入研究.路堤沉降与下部复合地基的沉降有着密切关系,准确计算下部复合地基沉降对路堤沉降的计算具有重要的意义.

目前复合地基的沉降计算方法思想主要是把沉降分为加固区沉降和非加固区沉降两部分来考虑.主要方法有规范方法、桩身压缩量法、双层应力法和附加应力法.其中：规范方法[11]将加固区看成一个整体并用复合模量表示其整体的压缩能力,通过Boussinesq解计算应力,采用分层总和法计算加固区和非加固区沉降；桩身压缩量法[12]将复合地基的沉降看成是由桩身压缩量和桩端刺入变形组成,该方法在确定桩的荷载分担值时主要依赖于经验；双层应力法[13]认为加固区土体和下卧层土体中的应力可分别用Boussinesq解获得,进而分别求解加固区和下卧层的沉降,其桩间土顶面和下卧层顶面应力水平的不确定性较大；附加应力法[14-15]是基于Mindlin解推导土体中的附加应力进而求解土体的压缩变形量,但仍是基于均质土体进行考虑的,这与实际情况明显不同,误差偏大.

基于此,本文提出了一种桩承式路堤沉降的计算方法,可分别计算桩顶沉降和桩间土沉降.将桩顶沉降分为桩端沉降、桩侧摩阻力引起的沉降及桩身压缩,采用球孔扩张法计算桩端荷载,桩侧摩阻力引起的沉降可通过Vesic解求得.将桩间土沉降分为桩间土表面荷载、桩侧摩阻力和桩端力引起的沉降.桩端沉降和桩间土沉降均认为是由地基土的附加应力引起,路堤荷载作用下地基土任意点的附加应力通过考虑多土层的非均质地基土情况利用修正Mindlin解求得.将本文提出的计算方法所得结果与现场实例和数值分析结果进行比较,以验证该方法的合理性.

1　简化计算方法的建立

为方便接下来的公式推导,作出如下假设:

(1) 路堤填土是均质、各向同性的材料;(2) 每一层地基软土是均质、各向同性且仅发生竖向变形;(3) 桩身刚度足够大不会产生破坏;(4) 不考虑土工格栅的影响,路堤填土的高度足够形成完整土拱.

1.1　土拱效应

1.1.1正方形布桩

Hewelett等[16]根据模型试验观测的结果认为,在正方形布桩情况下,桩间将形成一个半球形土拱和4个平面土拱,如图1所示.其中半球形土拱以相邻对角桩的桩间距为直径,相邻土拱存在部分重叠.土拱的极限状态仅可能出现在两个位置:土拱拱顶和拱脚.取桩的荷载分摊比较小的情况作为实际工作状态.

(1) 拱顶达到极限状态

根据拱顶单元的竖向力平衡,土拱单元的法向应力为[16]

(1)

(2)

式中:r为路堤填土的重度；H为路堤填土高度;Kp为朗肯被动土压力系数;s为桩间距；γ为路堤填土的重度;φs为路堤填土的内摩擦角,对于黏性土而言,其等效内摩擦角φeq,s=arctan(tanφs+c/γH)，其中，c为桩端土的黏聚力.

因此,桩间土中间处所受到的荷载为

(3)

式中:a为桩帽宽度.

式(3)求得的实际上是桩间土压力的最大值,而桩间土应力并非均匀分布,尤其对软土地基而言.考虑地基表面荷载分布不均匀性[17],引入均匀系数μ，则桩间土表面等效均布荷载为

σbs=μσs.

(4)

桩的荷载承担比为

(5)

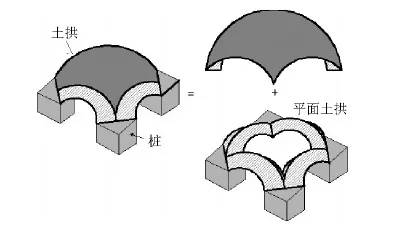
图1　土拱模型Fig.1　Arching model

(2) 拱脚达到极限状态

当拱脚单元处于极限状态时,土拱内边界的法向应力认为等于Kpσbs.根据拱脚土体单元的法向力平衡可得到土拱的法向应力为[16]

(6)

单个桩帽受到的合力由附近4个平面应变土拱产生,每个平面土拱均占据1/4桩帽面积.桩帽受到的合力可通过对桩帽上的不同半径处应力进行积分得到,即

(7)

根据竖向荷载平衡,可得到

Pt+σbs(s2-a2)=γHs2.

(8)

由(8)可得到σbs,进而可求得桩的荷载分摊比.

1.1.2三角形布桩

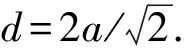
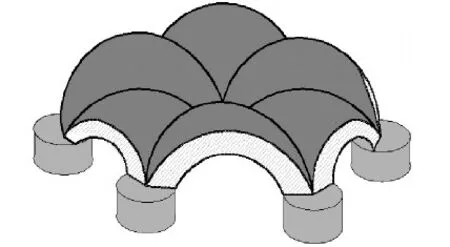
图2　三角形布桩的土拱模型Fig.2　Arch supported by piles arranged in triangle pattern

(1) 拱顶达到极限状态

(9)

因此桩间土中间处所受到的荷载为

(10)

由式(4)、(5)和(10)可求得桩的荷载分摊比.

(2) 拱脚达到极限状态

单个桩帽受到的合力由附近6个平面应变土拱产生,每个平面土拱均占据1/6桩帽面积.因此桩帽受到的合力也可通过对桩帽上的不同半径处应力进行积分得到,即

(11)

同样根据式(8)可求得桩间土表面等效均布荷载σbs,进而可求得桩的荷载分摊比.

1.2　桩顶沉降计算

单桩桩顶沉降Spt可认为由3部分组成:桩端力引起的桩端沉降Spb,桩身压缩量Spc和桩侧阻力引起的沉降Sps,即

Spt=Spd+Spc+Sps.

(12)

1.2.1桩端Vesic球孔扩张理论

Yasufuku和Hydea[18]通过试验观察到桩端的向下刺入类似于球孔扩张过程.因此,引入Vesic球孔扩张理论[19]进行桩端阻力计算,则桩端应力可表示为

(13)

式中:σ0为桩端平均应力;φ为桩端土的内摩擦角.

群桩基础的桩间距一般都小于6倍桩径,考虑到相邻桩之间的横向相互挤压,对桩端下刺具有抑制作用,桩端阻力可近似计算为[20]

(14)

1.2.2桩端沉降计算

对于均质弹性半空间体内深度h处作用集中力P时,深度z处任意点的竖向应力可表示为[21]

(15)

式中:R1、R2为计算半径,R1=(D2+(z-h)2)1/2,R2=(D2+(z+h)2)1/2;ν为土体的泊松比;D为所求点与集中力作用点的水平距离.

将桩端荷载看成圆形均布荷载,采用圆柱坐标系,力的作用点坐标为(r0,θ0,L),任意一点的坐标为(r1,θ1,z),两点的水平距离为

(16)

在圆形均布荷载选取一个面积元荷载dP=σptrdφdr,其在地基内任意点引起的附加应力为

(17)

桩端荷载在地基内任意点的附加应力可通过在圆形面积内积分求得,即

(18)

对于群桩基础而言,显然与半无限弹性空间体这一前提条件不符.因此本文认为在单根桩的处理范围内满足Mindlin解的前提条件.对于正方形布置的群桩,仅考虑单桩处理范围内的桩和桩间土荷载的影响.

根据桩间土表面荷载是均匀分布的假定,桩间土表面荷载在地基内任意点产生的附加应力为

(19)

桩端下部土层内任意点的附加竖向应力为

σz=σz1+σz2.

(20)

对于成层地基而言,可将每个土层看成半无限空间体,对每个土层分别采用Mindlin公式求解,令第i-1层土层下边界的附加应力为σ(i-1)b,第i层土层上边界的附加应力为σit,根据边界附加应力连续条件,可得到

σ(i-1)b=σiz.

(21)

根据式(19)、(20)和(21)即可求得成层土地基任意点的附加应力，随后利用分层总和法可得到桩端荷载和桩间土表面荷载在桩端持力层产生的附加应力引起的持力层压缩,即为桩端的沉降量Spb.

1.2.3桩身压缩量

一般来说,桩身压缩量的计算是先将桩分成若干段,假定整根桩的桩身横截面积不变,桩身弹性模量不变,分别计算每一段桩身的压缩量,然后将各段的桩身压缩量相加即可得到整根桩的桩身压缩量,但这需要对桩身的轴力分布有明确认识,通常情况下较难实现.张乾青[22]通过现场试桩静载试验发现,分段计算得到的全桩长桩身压缩量略大于直接利用桩顶荷载和桩端力计算得到全桩长桩身压缩量,极限荷载下分段计算的桩身压缩量接近于桩身实际压缩量,两者的比值为0.86～0.93.本文为简化计算,直接利用桩顶荷载和桩端力计算全桩长桩身压缩量，即

(22)

式中:Ap为桩身横截面积;Ep为桩身弹性模量;d为桩的直径;χ为修正系数,本文建议χ=1.10.

1.2.4桩侧阻力引起的沉降

将桩周土体假设为弹性各向同性的弹簧单元,其性质与土体的变形模量和泊松比有关,则桩侧阻力引起的沉降Sps为[23]:

(23)

(24)

式中:L为桩长;Es为地基土的压缩模量.

若地基土含有多层土层,则地基土的复合压缩模量可通过式(25)求解[24].

(25)

式中:h1(Es1)、h2(Es2)、…、hn(Esn)为成层地基的第1层、第2层、…、第n层的土层厚度(弹性模量).

1.3　桩间土沉降计算

桩间土沉降可认为由桩间土表面荷载、桩侧摩阻力和桩端力产生的附加应力引起,求解三者在地基中引起的附加应力是计算桩间土沉降的前提.桩端力和桩间土表面荷载产生的附加应力可分别采用式(14)、(15)进行求解.

桩侧摩阻力的分布对计算桩侧摩阻力在地基内任意点引起的附加应力至关重要.当路堤填土荷载较小时,桩土相对位移较小,桩侧摩阻力处于弹性阶段,此时桩侧摩阻力和桩土相对位移呈线性关系;当路堤填土荷载较大时,桩侧摩阻力与桩土相对位移呈非线性关系.在本文分析中,为简化计算,假定桩侧摩阻力沿深度呈三角形分布.

桩侧某处的摩阻力在地基内任意点引起的附加应力为

(26)

桩侧总的摩阻力在地基内任意点引起的附加应力为

(27)

对于成层土而言,可采用式(20)、(21)和(27)求解.同理,根据桩间土表面荷载、桩侧摩阻力和桩端力产生的附加应力,可通过分层总和求得桩间土沉降.

2　计算方法的验证

为验证本文计算方法的合理性,选取两个桩承式路堤算例进行分析,将本文方法的计算结果与现场实测和数值分析结果进行对比.

2.1　算例1

现场实测数据采用Briancon等[25]对桩承式路堤沉降的监测数据.测试地点位于巴黎东北部20 km 处的一处铁路路基,软土层主要由低塑性的粘土和砂质粘土,具有中度压缩性,软土层下部为致密砾石层.仅采用桩基础加固路段的路堤填高均为5 m,桩的直径均为0.30 m,间距为2 m的正方形布桩,各桩桩端均嵌入致密砾石层0.3 m.土体物理力学参数参考文献[25-26],列于表1、2.路堤高度足够形成完整土拱,计算桩长取8.8 m.

由于参数未给出压缩模量,因此根据上述参数,进行压缩模量的求解.一般来说,对于土的压缩曲线,采用半对数坐标表示成e-lgp曲线,其分为两段:曲线段和斜直线段.斜线方程可表示为

(28)

(29)

式中:Cc为e-lgp曲线的直线段压缩指数;pc为压缩曲线的转折点对应的压力;e为压缩曲线的转折点对应的孔隙比;p为作用在土体上的压力;e0为压力为p时对应的孔隙比；av为土的压缩系数.

令mv为土体的体积压缩系数,体积压缩系数与压缩模量存在倒数关系.根据体应变与垂直压力成正比,土体体积压缩系数与压缩指数关系如式(30).

(30)

将式(28)和(29)代入到式(30)中,可得

(31)

因此可求得下部致密砾石的压缩模量为6.38 MPa,软土的等效压缩模量为1.66 MPa.根据土拱效应计算得到两种状态下桩的荷载分摊比分别为0.736(拱顶极限状态)和0.373(拱脚极限状态).取拱脚极限状态进行分析,Pt=137.9 kN,σbs=60.2 kPa.根据式(14)计算得到σpb=753.7 kPa,桩端沉降为7.21 mm,桩侧摩阻力引起的沉降为0.37 mm,桩身压缩量为0.04 mm.将计算结果与现场实测数据以及文献[26]中的数值分析数据列于表3.由表3可知,本文提出的计算方法计算得到的桩顶沉降与现场实测相当接近.

表1　土体物理力学参数Tab.1　Physical and mechnical parameters of soil

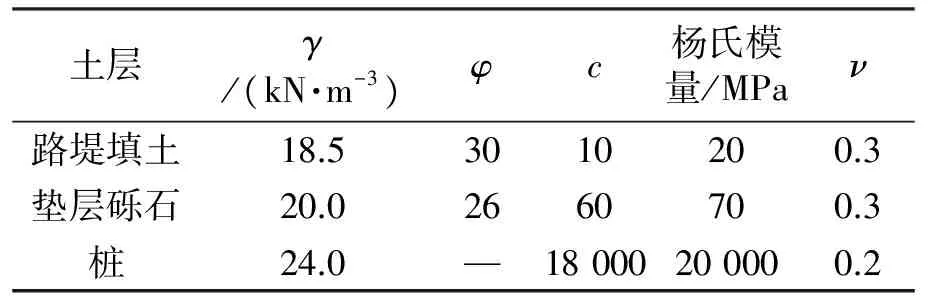
表2　路堤填土、致密砾石和桩的参数Tab.2　Parametes of soil and pile

表3不同计算方法得到的桩和土沉降
Tab.3Calculated and observed settlement of pile and soilmm

不同方法本文理论计算现场实测结果数值分析结果桩顶7．689．9桩间土92．410567．0

2.2　算例2

Chen等[8]利用数值分析方法计算了两种工况下桩承式路堤.工况1:桩长20 m,地基土为25 m厚的软土层,软土层下部为硬土层;工况2:桩长为27 m,软土层为25 m,软土层下部为硬土层.将计算结果与其提出的计算模型进行对比,计算模型的几何参数以及材料物理力学参数如表4所示.理论计算结果和数值分析结果如表5所示.

表4　模型的几何参数和材料物理力学参数Tab.4　Material properties used in the numerical modeling and the proposed analytical solution

表5不同计算方法得到的沉降
Tab.5The settlement by theoretical methods and numerical anaysismm

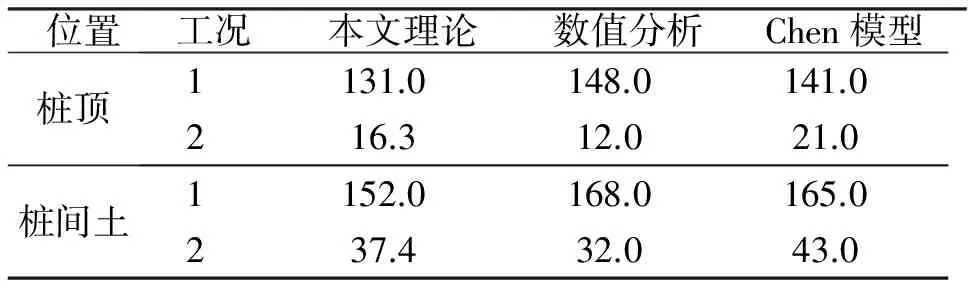
位置工况本文理论数值分析Chen模型桩顶1131．0148．0141．0216．312．021．0桩间土1152．0168．0165．0237．432．043．0

由表5可知：对工况1,本文方法与Chen的数值分析和计算模型结果吻合良好,说明本文方法和Chen计算模型在土层为均质条件下可较准确的预测桩顶沉降；对工况2,本文计算方法结果与数值分析结果仍吻合较好,说明本文方法能较准确地预估路堤荷载下悬浮桩和嵌固桩复合地基的沉降.

3　结束语

本文提出了一种软土地基桩承式路堤沉降的简化计算方法.考虑土拱效应对路堤荷载分配的影响,求得桩顶荷载和桩间土表面荷载,在此基础上将桩间土沉降分为桩间土表面荷载、桩侧摩阻力和桩端力引起的沉降,桩顶沉降分为桩端沉降、桩侧摩阻力引起的沉降及桩身压缩.桩间土沉降和桩端沉降均认为是由地基土中附加应力引起的,且成层地基土任意点的附加应力可通过改进的Mindlin解求得.通过将计算与现场实测结果进行对比发现,计算与实测结果吻合良好,说明本文方法的可靠性.

参考文献:

[1]MAGAN J P.Methods to reduce the settlement of embankments on soft clay:a review[J].Vertical & Horizontal Deformations of Foundatio Embankments,2015， 1(40):77-91.

[2]LIU H L,NG C W W,FEI K.Performance of a geogrid-reinforced and pile-supported highway embankment over soft clay case study[J].Journal of Geotechnical and Geoenvironmental Engineering,2007,133(12):1483-1493.

[3]陈云敏,贾宁,陈仁朋.桩承式路堤土拱效应分析[J].中国公路学报,2004,17(4):1-6.

CHEN Yunmin,JIA Ning,CHEN Renpeng.Soil arch analysis of pile-supported embankments[J].Chinese Journal of Highway and Transport,2004,17(4):1-6.

[4]LU W H,MIAO L C.A simplified 2-D evaluation method of the arcing effect for geosynthetic-reinforced and pile-supported embankments[J].Computers and Geotechnics,2015,65(65):97-103.

[5]ABUSHARAR S W,ZHENG J J,CHEN B G,et al.A simplified method for analysis of a piled embankment reinforced with geosynthetics[J].Geotextiles and Geomembranes,2009,27(1):39-52.

[6]EEKELEN S J M V,BEZUIJEN A,TOL A F V.Validation of analytical models for the design of basal reinforced piled embankments[J].Geotextiles and Geomembranes,2015,43(1):56-81.

[7]ZHANG C L,JIANG G L,LIU X F,et al.Arching in geogrid-reinforced pile-supported embankments over silty clay of medium compressibility:field data and analytical solution[J].Computers and Geotechnics,2016,77:11-25.

[8]CHEN R P,CHEN Y M,HAN J,et al.A theoretical solution for pile-supported embankments on soft soils under one-dimensional compression[J].Canadian Geotechnical Engineering,2008,45(6):611-623.

[9]HAN J,OZTOPRAK S,PARSON R L,et al.Numerical analysis of foundation columns to support widening of embankments[J].Computers and Geotechnics,2007,34(6):435-448.

[10]SHAHIRA H,PAK A.Estimating liquefaction-induced settlement of shallow foundation by numerical approach[J].Computers and Geotechnics,2010,37(3):267-279.

[11]中国建筑科学研究院.JGJ79—2012 中华人民共和国行业标准建筑地基处理技术规范[S].北京:中国建筑工业出版社，2012.

[12]龚晓南.复合地基理论及工程应用[M].北京:中国建筑工业出版社,2002:150-151.

[13]池跃君,宋二祥,陈肇元.刚性桩复合地基沉降计算方法的探讨及应用[J].土木工程学报,2003,36(11):19-23.

CHI Yuejun,SONG Erxiang,CHEN Zhaoyuan.An simplified method for settlement of rigid-pile composite foundation[J].China Civil Engineering Journal,2003,36(11):19-23.

[14]闫宝杰,宋修广,岳越群.粉喷桩复合地基附加应力的Boussinesq-Mindlin联合解法[J].岩土力学,2007,28(6):1255-1258.

YAN Baojie,SONG Xiuguang,YUE Yuequn.Boussinesq-Mindlin united solution method for DJMP composite foundation additional stress[J].Rock and Soil Mechanics,2007,28(6):1255-1258.

[15]陈永辉,王新泉,刘汉龙,等.Y型桩桩侧摩阻力产生附加应力的分析计算[J].岩土力学,2008，29(11):2905-2911.

CHEN Yonghui,WANG Xinquan,LIU Hanlong,et al.Analysis and calculation of additional stress due to skin friction of Y-shaped vibro-pile[J].Rock and Soil Mechanics,2008， 29(11):2905-2911.

[16]HELWETT W J,RANDOLPH M F.Analysis of piled embankment[J].Ground Engineering,1988,21(3):12-18.

[17]LOW B K,TANG S K,CHOA V.Arching in piled embankments[J].Journal of Geotechnical Engineering,1994,120(11):1917-1938.

[18]YASUFUKU N， HYDE A F.Pile end-bearing capacity in crushable sands[J].Geotechnique,1995,45(4):663-676.

[19]VESIC A S.Bearing capacity of deep foundations in sand[J].Highway Research Record,1963,10(39):112-153.

[20]刘俊飞.铁路CFG复合地基沉降控制机理与计算方法研究[D].成都:西南交通大学,2011.

[21]MINDLIN R D.Force at a point in the interior of a semiinfinite solid[J].Physics,1936,7(5):195-202.

[22]张乾青.软土地基桩基受力性状和沉降特性试验与理论研究[D].杭州:浙江大学,2012.

[23]VESIC A S.Design of pile foundation[M].Washington:National Cooperative Highway Research Program Synthesis of Practice,1977:31-32.

[24]ZHUANG Y,WANG K Y,LIU H L.A simplified model to analyze the reinforced pile embankments[J].Geotextiles and Geomembranes,2014,42(2):154-165.

[25]BRIANCON L,SIMON B.Performance of pile-supported embankment over soft soil full-scale experiment[J].Journal of Geotechnical and Geoenvironmental Engineering,2011,138(4):551-561.

[26]ROWE R K,LIU K W.Three-dimensional finite element modelling of a full-sacle geosynthetic-reinforced,piled-supported embankment[J].Canadian Geotechnical Engineering,2015,52(12):2041-2054.