不同粒径胶结类岩石材料损伤模型研究

郑小龙，赵 奎，曾 鹏，龚 囱，廖 鑫

（1.江西理工大学 资源与环境工程学院，江西 赣州 341000；2.江西省矿业工程重点实验室，江西 赣州 341000）

0 引言

岩石材料是地质工程中重要的组成部分，在工程应用中比较常见，是由不同种矿物颗粒、裂隙和胶结物组合而成的复合体。岩石在受载过程中，其内部微裂纹逐步扩展成肉眼能够看见的宏观裂纹，最终导致失稳破坏，其损伤过程备受矿业、铁路等工程地质领域关注。为此，国内外研究学者不断地研究岩石损伤本构方程来研究岩石损伤。利用损伤理论来研究岩石等含有初始缺陷的材料，已被认为是最有效的研究方法[1]，并成立多门学科[2-3]。研究不同粒径类岩石材料的损伤特性对矿山、交通及地质等领域岩石的破坏机理研究具有重要的参考意义。

损伤理论研究岩石损伤是利用平均化的方式，从岩石内部矿物颗粒、晶体、微裂隙、微孔洞等细观尺度上研究各种损伤的形态、分布及演化规律，最终将所得研究结果描述到宏观力学行为中[4]。任建喜等[5]对岩石在荷载过程中的破坏进行CT扫描，分析应力-应变的全过程，推导出岩石破坏过程中损伤演化方程和本构方程；杨圣奇等[6]对大理岩进行单轴压缩试验，构造出岩石损伤本构模型的参数能够反映残余强度；张明等[7]基于三轴压缩试验，结合统计强度理论及连续损伤理论，构造了一种岩石统计损伤本构模型，描述材料非线性力学行为；高文华[8]以软岩为研究对象，着重在应力水平和时间上做研究推导，构造出本构方程；刘红岩[9]构造非贯通节理岩体动态损伤本构模型，对加载应变率和节理特性等影响岩体动态力学特性作了对比分析；李淑春和白卫峰等[10-11]分别就混凝土变形破坏和复杂荷载作用下，构造了不等强度混凝土损伤变量方程、损伤演化方程和三维正交各向异性统计损伤本构方程；贾善坡等[12]利用损伤势函数，构造泥岩弹塑性损伤本构模型并通过模型反映出泥岩软硬化行为特征。这些学者对损伤模型的发展研究作出重大贡献，但大部分是从改变加载方式等外在条件出发构造本构方程，岩石损伤特性与本身内在条件关系的研究鲜有报道。

研究以岩石内部矿物颗粒大小为出发点，开展了三种不同粒径（0.1～0.2 mm，0.2～0.5 mm，0.63～1 mm）高纯度石英砂胶结的类岩石材料损伤模型的研究，建立损伤本构方程，探讨不同粒径类岩石材料破坏全过程的损伤特性。

1 试验研究方案

1.1 试验装置及测试方法

试验采用加载控制系统，加载设备是由中国科学院武汉岩土力学研究所研制的RMT-150C岩石力学试验系统，该系统可实时准确地记录当前荷载、应力、位移、应变和时间等数据，并同步绘制载荷-位移，计算弹性模量、泊松比等。试验采用位移控制加载方式，速率为0.002mm/s。

1.2 试验研究内容

筛分 0.1～0.2 mm，0.2～0.5 mm，0.63～1 mm 三种不同粒径的高纯度石英砂粒，采用标准325号硅酸盐水泥作为胶结材料，质量浓度为70%，灰沙比（质量比）为1∶4，制作成标准直径50 mm×100 mm的圆柱体类岩石材料试样，在20℃标准恒温养护室养护28 d后，进行单轴压缩破坏试验，探究不同粒径类岩石材料单轴压缩直至破坏全过程的应力、应变变化特征，建立三种不同粒径类岩石材料损伤本构方程，通过分析损伤与应变的关系，研究不同粒径类岩石材料破坏全过程损伤演变过程等。

2 不同粒径类岩石材料损伤力学分析

单轴压缩类岩石材料至破坏，对试验数据进行统计并处理，其力学参数如表1所示。选取Ⅰ-2、Ⅱ-1、Ⅲ-1分别代表每一种粒径的类岩石材料试件作为研究对象，得出实际应力-应变曲线如图1实线所示。

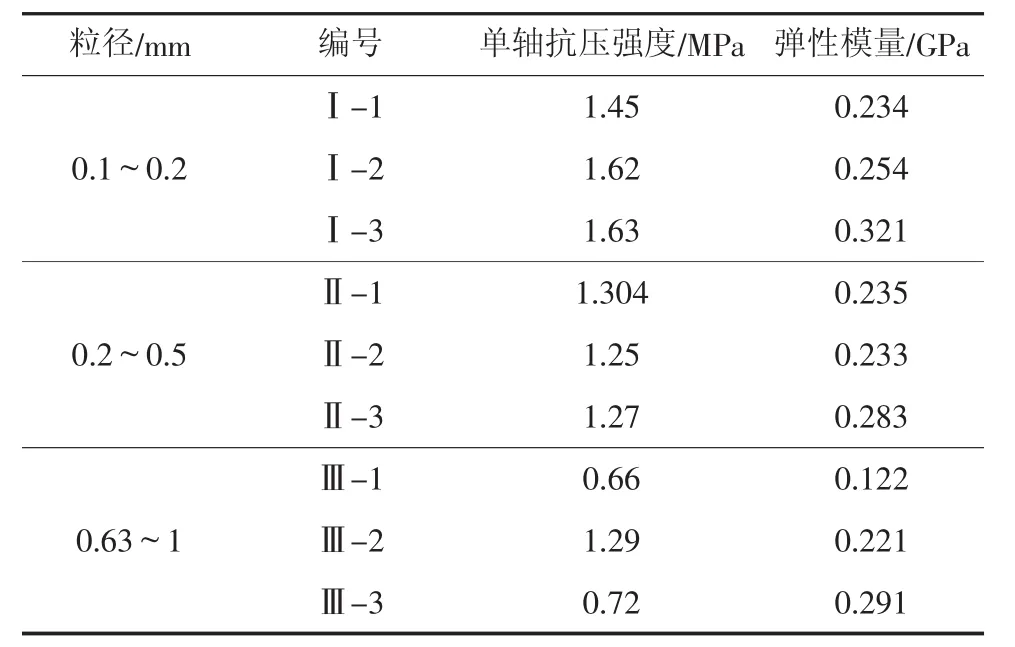
表1 不同粒径类岩石材料力学参数Tab.1 Mechanical parameter of backfill

从表1和图1可以看出三种不同粒径类岩石材料试件所表现出的力学性质差异主要与粒径有关，在一定的粒径范围内，粒径不同，其单轴抗压强度表现出较大差异，而对应的应变值相近。将应力-应变曲线分为四个阶段：

第一阶段为初始压密阶段（OA段），在应力-应变曲线中表现为下凹，斜率缓慢增大，这是类岩石材料预加载后其原始微裂隙、缺陷等被压密的结果。A点作为压密阶段终止点，预加载后粒径为0.2～0.5mm的试件该点对应的应力最大，占峰值强度的23.8%，而粒径0.1～0.2 mm及0.63～1 mm试件该点对应的应力分别占其峰值强度的12.5%和14.9%。

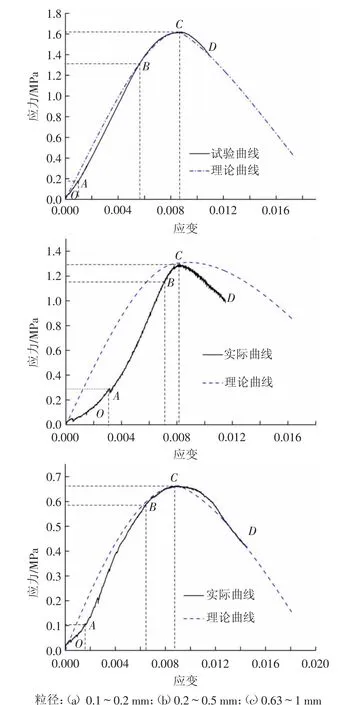
图1 不同粒径类岩石材料单轴应力-应变曲线Fig.1 Compressing stress-strain curves of backfill

第二阶段为弹性变形阶段（AB段），不同粒径类岩石材料的应力-应变曲线都表现为斜率几乎不变，近似直线；粒径为0.2～0.5 mm时斜率最大，而从表中可知弹性模量与粒径的关系表现不太明显。

第三阶段为屈服阶段（BC段），应力-应变曲线表现为斜率逐渐减小直至为0，粒径为0.1～0.2 mm的试件抗压强度最大，平均在1.6 MPa左右，屈服变形过程也最明显，粒径为0.63～1 mm类岩石材料试件抗压强度最小，平均抗压强度小于1 MPa，屈服变形过程不明显。

第四阶段为宏观破坏和破坏后阶段（CD段），此时应力-应变曲线斜率小于0，类岩石材料试件的应力随应变的增大而减小。峰值强度之后微裂纹迅速扩展，裂纹之间的岩桥破坏，宏观裂纹相互连接，形成更大的裂纹。与强脆性岩石不同的是，类岩石材料实际曲线的峰值后部分没有明显应力陡降，水泥胶结的类岩石材料表现出较强的延性。

综上所述，石英砂胶结类岩石材料单轴加载破坏全过程表现得比较圆滑，表现出较强的延性；三种不同粒径类岩石材料试件应力-应变曲线四个阶段所表现出的差异主要与粒径有关，在0.1～1 mm粒径范围内，随着粒径的逐渐变大，单轴抗压强度有减小趋势。

3 不同粒径类岩石材料损伤本构方程

3.1 损伤本构方程

视类岩石材料为各向同性的连续介质，刘志祥[14]根据应变等价原理构造出充填体损伤本构方程如式（1）～式（4），本文根据式（2）和式（4）得出类岩石材料损伤本构方程如表2。

峰值应力前本构方程和损伤演化方程：

峰值应力后本构方程和损伤演化方程：

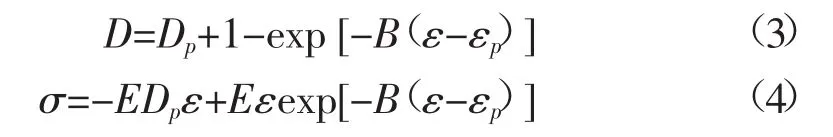
式中：D为损伤值，E为弹性阶段的变形模量（应力-应变曲线直线段斜率）；A、B和β为常数，可由边界条件求得。

表2 不同粒径类岩石材料损伤本构方程Tab.2 Constitutive equation for damage of rock material with different particle sizes

根据损伤本构方程，得到不同粒径类岩石材料理论应力-应变曲线如图1虚线所示。粒径为0.1～0.2 mm试件的理论应力-应变曲线和实际曲线基本吻合；对于粒径0.2～0.5 mm、0.63～1 mm试件来看，在达到C点之前，理论曲线表现为略微上凸形，试验实际曲线达到峰值C之前阶段为下凹形，这与该本构方程不能反映单轴压缩条件下试样变形的初始压密阶段有关[7]，其次还与试验时的试验操作误差等因素有关，但总体吻合。

3.2 不同粒径类岩石材料损伤特征分析

由试验结果，根据不同粒径试件的弹性模量及峰值强度对应的应变，计算三种不同粒径类岩石材料峰值应力所对应的损伤值见表3，粒径越大峰值应力所对应的损伤值越大。

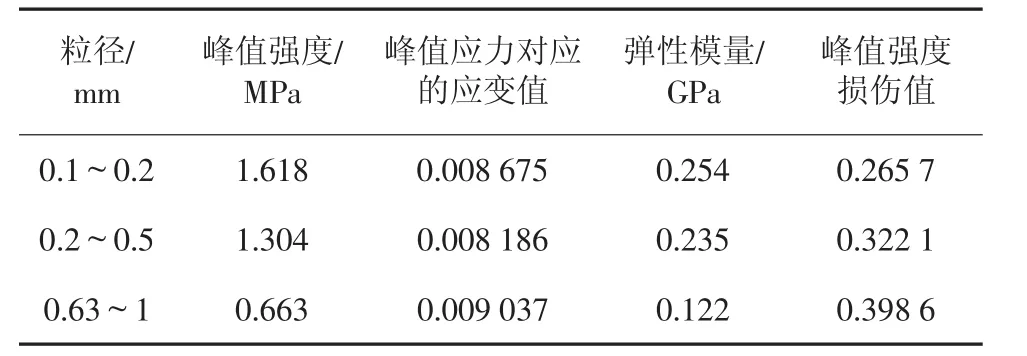
表3 不同粒径峰值强度对应损伤值Tab.3 Damage value of backfill with different particle size

由式（1）和式（3）计算得到不同粒径类岩石材料的损伤演化方程，并绘制出损伤演化曲线如图2所示。

图2中a、b点分别表示弹性阶段转塑性阶段分界点对应的损伤值及峰值应变对应的损伤值，粒径为0.1～0.2 mm、0.2～0.5 mm时，a点之前损伤值缓慢增加，在图中表现为损伤值-应变曲线斜率缓慢增大，而粒径0.63～1 mm试件表现为增长稳定；ab之间三种粒径的曲线斜率增加都比较明显，说明塑性阶段损伤增速；b点之后斜率骤增。

图2 不同粒径岩石材料的损伤演化曲线Fig.2 Damage value-strain curves of backfill

峰值应力前，粒径为0.63～1 mm试件损伤相对最大，而粒径为0.1～0.2 mm试件损伤最小；峰值应力后，粒径为0.1～0.2 mm的类岩石材料试件表现得最为明显，增长速率最快，而粒径为0.63～1 mm试件增长速率最小。说明在0.1～1 mm的粒径范围内，粒径越小，峰值应力前损伤值越小，峰值应力后损伤值增长越快，破坏越突然。

4 峰值比能分析

本文定义单位体积的变形能为比能，峰值强度时的总比能就称为峰值比能。文献[13]给出了峰值比能的计算过程，根据有效应力能量等价原理[14]，在损伤的前提下，可结合有效应力计算类岩石材料的弹性变形比能。假设单元体的应力从0慢慢增大到σx，对应发生的变形为εx，则单元体的弹性变形可用式（5）计算：

试件达到峰值应力σx时所对应的应变为εx，结合式（2）和式（5）推演化简得到类岩石材料试件峰值应力时的变形比能Up：

通过前面所得峰值应力前的损伤本构方程，由式（6）计算得到峰值应力时的变形比能如表4所示。

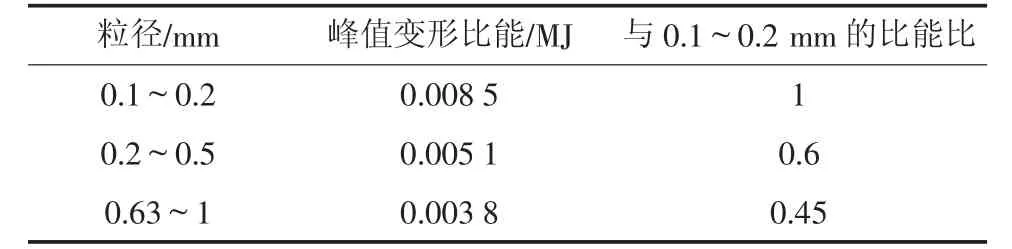
表4 不同粒径试件峰值强度变形比能Tab.4 Peak energy of backfill with different particle size

由表4可知，粒径为0.1～0.2 mm的类岩石材料试件峰值强度时的变形比能为0.008 5 MJ，而粒径为0.63～1 mm的试件峰值强度时变形比能为0.0038MJ，说明粒径越小，峰值比能越大。

5 结果分析与讨论

5.1 结果分析

（1）不同粒径组成的类岩石材料力学特性和损伤特性表现出不一样的规律，粒径为0.1～0.2 mm的类岩石材料抗压强度在1.6 MPa左右，而粒径为0.63～1 mm时最小，平均抗压强度小于1，弹性模量与粒径关系则不明显。

（2）在粒径为0.1～1 mm范围内，粒径越大，峰值应力前损伤也明显更大，而峰值应力后恰恰相反，粒径越小，损伤值增长的越快，破坏越突然，表明岩石内部颗粒越小，其破坏后期表现越明显。

（3）峰值变形比能方面，粒径为0.1～0.2 mm的类岩石材料试件峰值强度时变形比能最大，而粒径为0.63～1 mm的试件峰值强度时变形比能最小。在一定程度揭示了，岩石内部颗粒越大，峰值应力时变形比能越小。

5.2 讨论

在已有的研究中，单纯针对矿物颗粒的试验研究相对较少，得到粒径与强度的关系也不尽相同。理论研究上，有学者利用pfc软件模拟矿物粒径在1.5～3 mm范围时岩体的力学性能，粒径为1.5 mm的试件单轴抗压强度最小，3 mm时最大，反映出矿物颗粒越大，强度越高[15]，与试验结果有所出入。根据以上论述，笔者认为针对试验结果有必要对试验研究中可能会影响类岩石材料强度的因素进行分析，大概有以下几点：

（1）试件粒度配比：试验研究使用的骨料粒径范围分别为0.1～0.2 mm，0.2～0.5 mm，0.63～1 mm 的高纯度石英砂，最大粒径与最小粒径差分别为0.1mm、0.3 mm、0.37 mm，这导致了各粒径试件粒度配比有所差别，出现如文献[16]的现象。

（2）类岩石材料模型浇筑：浇筑类岩石材料时所使用的灰砂比、水灰比及水泥强度等是影响试件强度的重要因素。其次还有脱模时脱模机对试件的破坏程度。

有时这些因素导致了研究岩石力学性质、损伤特性与材料内部颗粒关系的复杂性，在试验研究方面进展缓慢。这也说明针对岩石内部粒径的研究还有工作要做，可以从改变骨料类型，粒径范围等方面着手。

参考文献：

[1] 王创业，刘 伟，杜晓娅.基于声发射的岩石损伤演化特征分析[J].中国钨业，2017，32（5）：17-20，57.WANG Chuangye，LIU Wei，DU Xiaoya.Analysis of rock damage evolution based on acoustic emission[J].China Tungsten Industry，2017，32（5）：17-20，57.

[2] LEMAITREJ.How to use damage mechanics[J].Nuclear Engineering and Design，1984，80（2）：233-245.

[3] 余寿文.损伤力学[M].北京：清华大学出版社，1997：1-315.

[4] 张全胜，杨更社，任建喜.岩石损伤变量及本构方程的新探讨[J].岩石力学与工程学报，2003，22（1）：30-34.ZHANG Quansheng，YANG Gengshe，REN Jianxi.New study of damage variable and constitutive equation of rock[J].Chinese Journal of Rock Mechanics and Engineering，2003，22（1）：30-34.

[5] 任建喜，葛修润.单轴压缩岩石损伤演化细观机理及其本构模型研究[J].岩石力学与工程学报，2001，20（4）：425-431.REN Jianxi，GE Xiurun.Study of rock meso-damge evolution law and its constitutive model under uniaxial compression loading[J].Chinese Journal of Rock Mechanics and Engineering，2001，20（4）：425-431.

[6] 杨圣奇，徐卫亚，韦立德，等.单轴压缩下岩石损伤统计本构模型与试验研究[J].河海大学学报自然科学版，2004，32（2）：200-203.YANG Shengqi，XU Weiya，WEI Lide，et al.Statistical constitutive model for rock damage under uniaxial compression and tis experimental study.[J]Journal of Hohai University（Natural Sciences），2004，32（2）：200-203.

[7] 张 明，王 菲，杨 强.基于三轴压缩试验的岩石统计损伤本构模型[J].岩土工程学报，2013，35（11）：1965-1971.ZHANG Ming，WANG Fei，YANG Qiang.Statistical damage constitutive model for rocks based on triaxial compression tests[J].Chinese Journal of Geotechnical Engineering，2013，35（11）：1965-1971.

[8] 高文华，陈秋南，黄自永，等.考虑流变参数弱化综合影响的软岩蠕变损伤本构模型及其参数智能辨识 [J].土木工程学报，2012（2）：104-110.GAO Wenhua，CHEN Qiunan，HUANG Ziyong，et al.Study on the creep damage constitutive model of soft rocks considering rheological softening and intelligent identification of the parameters[J].China Civil Engineering Journal，2012（2）：104-110.

[9] 刘红岩，吕淑然，张力民.基于组合模型法的贯通节理岩体动态损伤本构模型[J].岩土工程学报，2014（10）：1814-1821.LIU Hongyan，LYU Shuran，LI Limin.Dynamic damage constitutive model for persistent jointed rock mass based on combination model method[J].Chinese Journal of Geotechnical Engineering，2014（10）：1814-1821.

[10] 李淑春，刁 波，叶英华.反复荷载作用下的混凝土损伤本构模型[J].铁道科学与工程学报，2006，3（4）：12-17.LI Shuchun，DIAO Bo，YE Yinghua.Damage constitutive model concrete under cyclic loading [J].Journal of Railway Science and Engineering，2006，3（4）：12-17.

[11] 白卫峰，张树珺，管俊峰，等.混凝土正交各向异性统计损伤本构模型研究[J].水利学报，2014，45（5）：607-618.BAI Weifeng，ZHANG Shujun，GUAN Junfeng，et al.Orthotropic statistical damage constitutive model for concrete [J].Journal of Hydraulic Engineering，2014，45（5）：607-618.

[12] 贾善坡，陈卫忠，于洪丹，等.泥岩弹塑性损伤本构模型及其参数辨识[J].岩土力学，2009，30（12）：3607-3614.JIA Shanpo，CHEN Weizhong，YU Hongdan，et al.Parameter identification of new elastoplastic damage constitutive model for claystone[J].Rock and Soil Mechanics，2009，30（12）：3607-3614.

[13] 刘志祥，李夕兵，戴塔根，等.尾砂胶结充填体损伤模型及与岩体的匹配分析[J].岩土力学，2006，27（9）：1442-1446.LIU Zhixiang，LI Xibing，DAI Tagen，et al.On damage model of cemented tailings backfill and its match with rock mass[J].Rock and Soil Mechanics，2006，27（9）：1442-1446.

[14] 于骁中.岩石和混凝土断裂力学[M].长沙：中南工业大学出版社，1991：85-99.

[15] 许尚杰，尹小涛，党发宁.晶体及矿物颗粒大小对岩土材料力学性质的影响[J].岩土力学，2009，30（9）：2581-2587.XU Shangjie，YIN Xiaotao，DANG Faning.Mechanical characteristics of rock and soil affected by particle size of crystal and mineral[J].Rock and Soil Mechanics，2009，30（9）：2581-2587.

[16] 孙凯年，刘可任.尾砂粒度对充填体物理力学性质的影响[J].有色金属工程，1983（3）：16-24.SUN Kainian，LIU Keren.Influence of tailings particles on physical and mechanical properties of fill[J].Nonferrous Metals，1983（3）：16-24.