结合高考的高一数学教学例谈

梁笛

（陕西师范大学数学与信息科学学院，陕西西安　710062）

本文结合高考要求回归高一的基础教学，以北师大版高中数学必修一内容为例从教师用好教材变式教学，学生用好教材举一反三的角度谈谈教师如何在起始年级的数学教学中帮助学生构建良好的数学知识体系，培养学生优秀的数学思维品质，建立学生科学的数学学习方法。

1　教师如何用课本教

1.1　依据教材而不拘泥于教材

公平、公正地对待各个版本，不刻意向某一版本倾斜，在平时的教学中宜参考不同版本，整合各版本引入、例题、习题方面的优点，选择适合本班学生认知水平、接受能力的内容在课堂教学中使用。

例如：《北师版高中数学必修一第三章第六节》在进行处理的时候以繁琐、复杂的运算和生硬枯燥的表格呈现出三种函数的增长，缺乏直观性、趣味性，经常让教师不知如何指导学生使用这节内容，而往往学生也会在这节课学完以后只是机械的记住：当a＞1，指数函数y=ax与对数函数y=logax都是增函数，a越大，函数值的增长就越快；当 x＞0，n＞1时，幂函数 y=xn也是增函数，并且当x＞1时，n越大其函数值的增长就越快。当三类函数一起比较时，当x足够大时，必有指数函数的增长最快，人们称这种现象为“指数爆炸”。

学生对于三种函数增长变化的印象仅仅停留于此，可能没有更多的兴趣进一步去研究它们了。

但是湘教版在处理这节课的时候就精彩有趣很多，我们一起欣赏一下它的引入。

引例：以幂函数模型图象变化快慢切入。

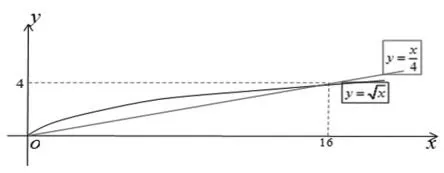
图1

这样的引用通俗易懂，妙趣横生，将学生代入利用图象研究函数的氛围之中，后续课程的铺开便显得很自然。

1.2　以课本例题和习题为基本题根，进行变式教学，高站位，低起点

很显然，这道题是让学生从初中反比例函数的图象出发，直观感受单调性的。但是教师必须在学生的直观上建立严谨的证明，让学生从高中单调性定义出发给出此题单调性的严格证明，并进行以下的变式练习。

1.3　讲清课本基本定义并进行适合不同学生层次的引申

如函数的单调性定义：在函数y=f（x）的定义域的一个区间A上，如果对于任意两数x1，x2∈A，当x1＜x2时，都有 f（x1）＜f（x2），那么，就称函数 y=f（x）在区间 A上是增加的。

对于这样的定义，教师应该引导学生用等价的数学式子表达为：对于定义在A上的函数f（x），设x1，x2∈A，则有：

这就达到了在基础要求之上的第一层次的提升，而对于层次更好的学生或者随着学习的深入学生的思维得到提升以后，可以引导学生给出第二层次的探究。

2　学生如何用课本学

2.1　学会评价并欣赏课本解题思路，善于联系贯穿各个知识点

x∈[-1，2]的最大值与最小值。

2.2　总结、联系、整理由课本引出的变式练习

学生通过一段时间的积累便能发现这些题目之间的联系，同时在这种发现中展开了联想与想象的能力，也能更深刻的体会我们通常所说的“分离系数法”是怎样的一种方法，为何需要想到并且应用这种方法解题？这就比老师直接告诉学生方法要印象深刻得多，也让学生体会了更多的成就感，体会了发现数学方法的乐趣。

2.3　重视教材后面的阅读资料

在阅读资料中感受数学的文化魅力和应用价值，比如在进行了对数运算的学习之后我们可以通过对数换底进行大数的估算和比较，这不就是对数引入的初衷吗？阅读完相关材料后教师可以提供学生这样的问题：

已知 lg2=0.3010，1g3=0.4771（1）估计 2100的大小；（2）比较 2100与 365的大小。

解析：（方法一）设x=2100，等号两边同取以10为底的对数，得：

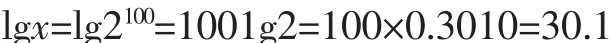
所以 x=1030.1=1030×100.1

（方法二）利用对数的常用恒等式alogaN=N

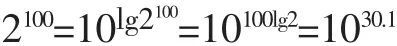
同理可以估算365的大小，进而很容易比较这两个数。一般计算器不好解决的计算问题，我们可以通过数学算法给出解答，这种数学应用意识和应用能力的培养建立了学生学习数学的兴趣和信心。

如果学生还想进一步探究，可以尝试把自己平时学习中的发现撰写成数学小论文，对学生的数学表达能力是很好的锻炼。也让学生在具体的“做”中学数学、感受数学、应用数学。

用好了教材，教师才能在课堂上教出新意，教出方法；用好了教材，学生才能在学习中学到方法，学出能力.教与学才充满了创造和乐趣.

[1]黄坪，尹德好.高中数学题根[M].上海：华东师范大学出版社，2013.

[2]严士健，李延林.普通高中课程标准实验教材数学1（必修）[M].北京：北京师范大学出版社，2004.

[3]张景中，黄楚芳.普通高中课程标准实验教材数学1（必修）[M].湖南：湖南教育出版社，2011.

[4]张扬文.高考数学你真的掌握了吗？函数[M].北京：清华大学出版社，2014.