基于通信时分框架的单站无源动目标定位技术

2018-04-10高元峰贾铁燕

无线电工程 2018年5期

高元峰，江　漫，葛　蕾，贾铁燕

(中国电子科技集团公司第五十四研究所，河北石家庄 050081)

0　引言

现代战争中各种高新技术兵器对于作战武器平台生存的威胁日趋严重，除了实现更多平台间的信息情报共享、资源协同支持，还要提升平台自身的综合作战能力，形成更大的感知域、拒止域和掌控域。

长久以来，武器平台的单站动目标定位技术都是其能力建设的重中之重，而主动探测手段由于原理简单、性能优越等特点长期占据主导地位，但随着各种电子对抗技术的发展，主动探测的电磁辐射风险日甚而其回报骤减，同时以被动相参定位(Passive Coherent Location，PCL)技术[1-3]为代表的单站无源定位技术开始不断发展。无源定位技术[4-6]具有良好的电磁隐蔽特征，同时其在反隐探测、设备成本方面具有较大优势，已经成为世界各国新技术手段发展的热点。

本文主要针对单站无源[7-8]动目标定位技术体制和基于通信时分结构下时差变化率[9-10]进行理论分析与仿真研究，较好地解决了单站径向探测的瓶颈限制和测量精度问题，提升了整体的定位能力。

1　　　　单站无源动目标定位体制分析及常规算法的技术限制

图1　单站无源定位基本模型

在具体应用算法研究中，会根据不同设定，补充三角形已知要素使其合理并可解。比如，当把点T设定为第三方电波辐射源(如广播电台等)，并利用直达波和折射波间的波程差估计(其本质是已知三角形一条边(c)、一个内角(∠TOA)和另一条边的条件(两边差))可以得到目标A的位置，即PCL的基本概念模型。

考虑到所提基础三角形模型的结构需要，有单运动平台对固定目标的无源定位技术研究，其设定目标A固定不动而侦测站O发生运动的条件。此时由于O的合作性运动导致随时间变化的一系列连续三角形，通过多次测角可统计交汇位置，从而得到对目标A的定位估计。

在固定单站无源定位技术的研究中，目标和侦测站间的径向位移测量模糊是十分棘手的难题。在图1的模型中，如果目标A运动则会得到一系列角αi，i=1，2...，i为观测时刻。显然有

(1)

近些年，有学者提出基于角度变化率、多普勒频率变化率、方向信息、角速度及多普勒频率变化率信息等技术方法实现单站无源动目标定位能力。其算法核心都是基于对多普勒频率估计推测目标的径向运动，同时算法对于对象的运动规律还有较多要求，不具备广泛的适应性和动态稳健性。

基于多普勒频率与变化率的方法，前提条件不是需要约束目标的运动规律(如匀速直线运动)，就是要求明确目标的运动速度或载波频率信息，其假设显然不具有良好的工程实用基础和应用前景。其中，多普勒频率直接反映了目标的相对运动速度和频率之间的物理关系，如果知道目标的多普勒频率就等于知道目标的径向运动速度。但对于非合作方获得目标的多普勒频率几乎是不可能达到的条件，因此该方法研究甚少。而多普勒频率变化率估计规避了目标频率已知的要求，通过连续测频得到频差的方式提取可用信息。而多普勒频率变化率反映目标径向速度的变化值，是目标运动加速度的直接物理体现，对其的研究依旧存在对运动规律的约定。如标准二维定位算法(要求目标做匀加速运动)、EKF[11-12]的定位与跟踪滤波算法(要求目标做平滑运动)等。

2　基于时差变化率增强的新定位技术

通信系统作为众多分散收发信息交互活动的支撑，需要具有严格的规则和固有的循环。现代通信系统中，时分复用[13]体制是解决多用户接入、低概率截获和提高资源利用率的重要方式。系统通过建立统一、标准化的时间基准框架，对通信带宽资源进行时间片划分，将不同用户和各种业务按需进行时隙(时间片)资源分配，而用户时隙以最大运行时间周期循环，即

(2)

式中，Tn为第n个时隙的结构集合；Δt为时隙的时间片宽度；T为整体时间运行周期。单个用户因需会获得1个以上的时隙资源分配，而在使用中用户也有个别具体时隙未使用的情况，但总体上其通信电磁行为总是发生在总周期T的整数倍时刻。

时隙结构及其规律是通信信号一种较为显著的特征，而在内部还有很多的同步、循环、固定的信息或结构。在对目标有一定分析和了解的基础上，都是可能成为提取其行为周期性特征的依据。

2.1　通信的时分复用原理和体制结构

通过对于定位目标电磁行为规律的掌握和时间序列的估计，可以提供一种核心三角结构关系的新理解。它区别于传统PCL等技术的突出特点是，通过研究目标，不单纯依靠基本物理信号参数测量，掌握并利用其上层电磁行为规律信息特征建立分析模型，其估计精度优势明显。需要强调的是此种估计可以替代之前多普勒频率及其变化率测量的方法，解决单站模型中径向测量模糊的难题。

建立基于通信时分框架的时差变化率增强单站无源动目标定位技术，其核心模型由固定侦测站O和运动目标A组成，t0，t1，...，tn...分别是不同的侦测时刻，以其中的t0，t1为例建立三角结构关系，结构如图2所示。

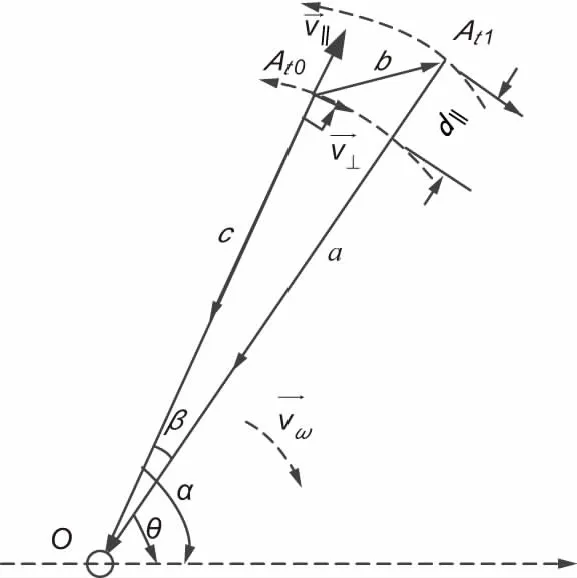
图2　时差变化率增强单站无源动目标定位模型

在该模型中，角α和θ是动目标t0，t1两个时刻的方向角，可用θi，i∈Z时刻i的方向角统一表示，角β=α-θ=θi-θi+1=Δθi，i+1代表方向角变化值。显然有

(3)

即估计足够高频度的测向序列值变化率，将收敛于目标运动的切向角度速。

2.2　新算法的流程

时差变化率增强单站无源动目标定位算法的定位模型如图2所示，其中角度α，β，θ可以通过测向设备测得，d||为由于目标径向运动分量引起的径向位移的变化，其求解可以通过周期信号的时差变化率乘以光速求得。因此，只要初始距离c可求，即距离信息加上方向信息可以唯一确定目标的位置。

新模型定位算法流程如图3所示。先对预求解的目标距离设定t0时刻未知变量c，再按照计算步骤顺序，依次开展数据演算估计。

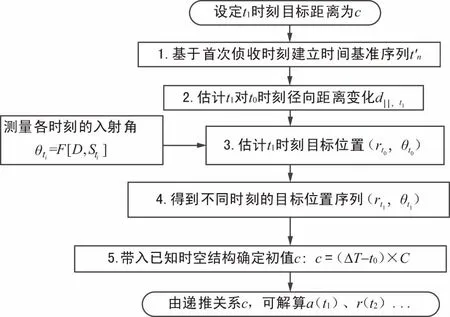
图3　时差变化率增强单站无源动目标定位算法流程

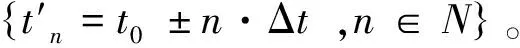
步骤2 显然当目标的位置与相对距离不发生变化时，侦测站将按以Δt为最小周期的时间序列收到其通信信号。而实际侦收信号时刻偏离时间基准序列就意味着其位置移动和距离(径向)变化，如式(4)计算相对时差值则可径向距离的变化量d‖。

DefineΔt′=(t1-t0)-Δt，d‖， t1=Δt′×C。

(4)

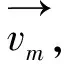
(5)

进而可以计算t1时刻目标的位置(rt0，θt0)=(rt0=c+Δt′×C，θt0)。

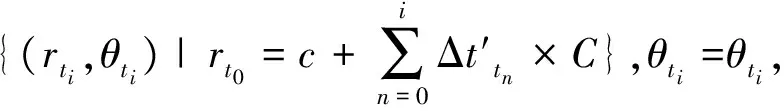
步骤5 很多目标的运动具有固定规律性，这集中表现为其运动过程的起点和终点确知。由此可唯一确定数学模型中的初始/终止距离c/cn，从而确定整个运动过程中的位置。

通过以上估计可得到对t0～tn时刻，运动目标位置距离ci的值，进而实现对运动目标的单站无源定位能力。

在动目标的径向距离估计研究中，传统使用多普勒频率[14]、多普勒变化率[15]和相位差变化率[16]等方法较多。而新方法掌握目标通信信号行为规律，并据此建立的时间基准序列，可以很好地描述目标的电磁信号特征，具有超越传统信号参数测量上界的性能指标。

2.3　算法定位参数提取

本文所介绍的定位技术主要由测向信息加上距离信息获得，而距离信息的求解精度依赖于与对目标电磁通信行为规律的掌握所建立的径向距离变化测量的精度，要由接收系统的信号截获时间精度所决定。而对于信号检测处理，理论上界为信号自相关函数，输出信噪比与信号自身能量相关，是其时宽带宽积的函数。基于时差的径向距离高精度估计，归根到底就是如何高精度地提取信号的到达时间，等价于如何高概率地检测截获突发信号。

时差会提高目标径向的距离测量进度，而系统整体定位的主要误差来自于单站DOA估计。在雷达、声纳等领域中，对于空间信号到达方向(DOA)估计的研究由来已久。基于阵列天线对DOA估计[17]的方法包括ARMA谱分析、最大似然法、熵谱分析和特征分解法等多种。其中传统的DOA估计方法，如Capon波束形成法[18-19]，在最小方差法(MVM)优化[20-21]求解后，可得到噪声与来自非θ方向的任何干扰贡献功率最小，又能保持θ方向上的信号功率。其估计结果为：

(6)

而MUSIC算法由噪声特征矢量和信号矢量的正交关系，得到阵列空间谱函数：

(7)

通过对于θ变化，扫描搜索空间中的波峰来估计到达角。而对其在理想情况下，估计误差协方差矩阵的克拉美-罗界分析有：

(8)

式中，S(i)=diag[s1(i)，s2(i)，...，sK(i)]。另外，噪声功率的克拉美-罗界为：

(9)

3　仿真对比与分析验证

3.1　新算法对各种运动规律适应性

本算法由于是对目标结果数据的后处理，且不需要对其运动规律模型的约束，所以算法表现出良好的运动适应性。算法对匀速直线运功的估计效果如图4所示，观察点为原点，目标从仰角5°距离10 km外出发，沿x轴做300 m/s的匀速直线运动，在无噪条件下可以达到10-4的定位误差。仿真显示将初始距离设为100 km时，其定位误差也小于10-2m。

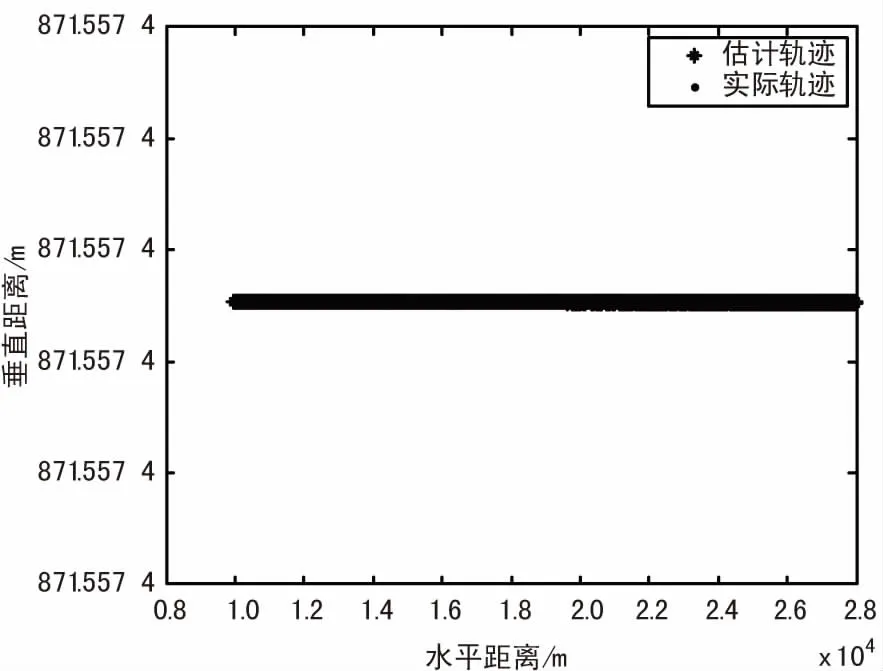
(a)定位轨迹线

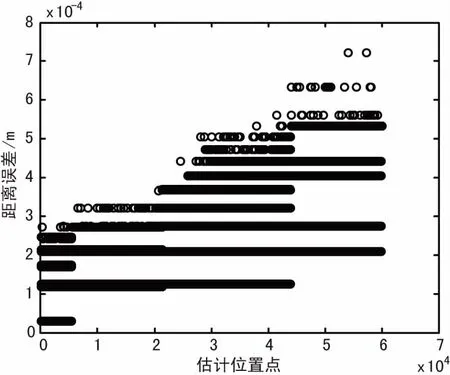
(b)定位轨迹误差

算法对曲线运功的估计效果如图5所示，观察点为原点，目标从仰角5°距离10 km外出发，沿x轴做初速300 m/s加速度仰角2°的曲线运动，在无噪条件下可以达到10-3的定位误差。仿真显示将初始距离设为100 km时，其定位误差也小于10-3m。

(a)定位轨迹线

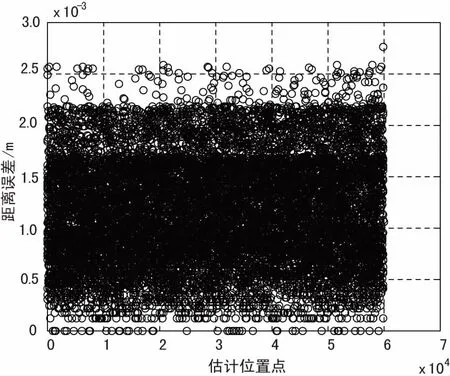
(b)定位轨迹误差

3.2　新算法对量化误差和信噪比的适应性

当算法考虑实际信号条件，引入量化误差和信噪比条件后可得到如图6所示的仿真结果。当考虑相位量化精度在0.1°，相位测量误差小于10°，目标距离80 km时典型定位误差在50 m以内。而当目标距离达到300 km时则达到200 m左右的误差。

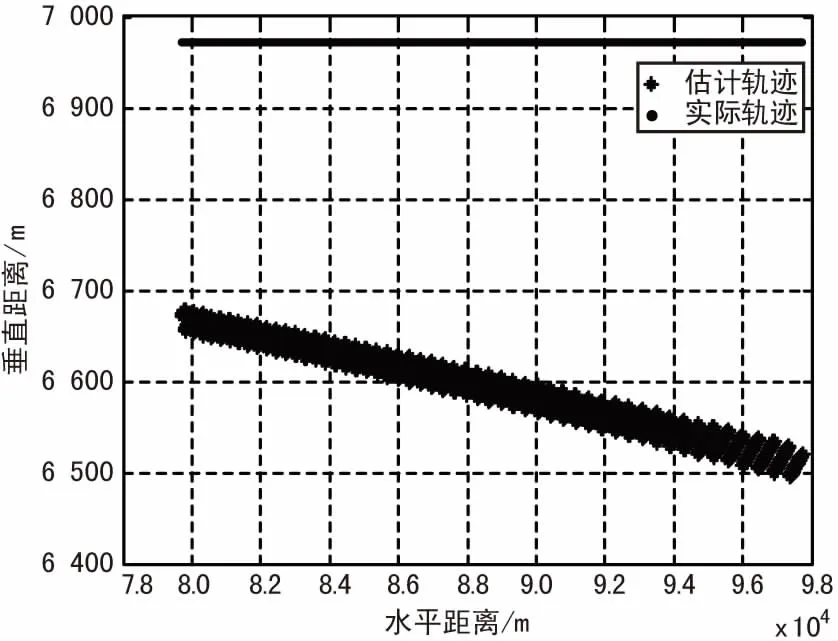
(a)定位轨迹线

(b)定位轨迹误差

当算法考虑实际信号条件，引入量化误差和信噪比条件后可得到如图7所示的仿真结果。当考虑相位量化精度在0.1°，相位测量误差小于10°，目标距离80 km时典型定位误差在100 m以内。而当目标距离达到300 km时则达到400 m左右的误差上限。

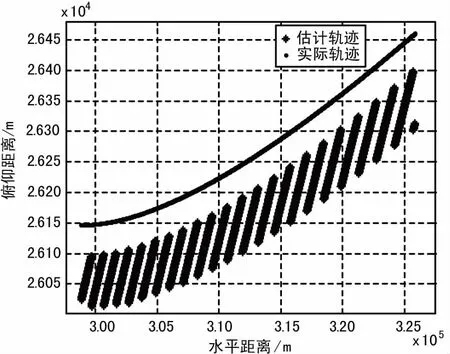
(a)定位轨迹线

(b)定位轨迹误差

结合以上仿真可知，新算法对目标的运动状态没有依赖，表现出良好的运动适应性，同时再引入量化误差和信噪比之后，由其所带来的误差也控制在1%R(R为侦测距离)之内，在可以容忍的误差范围内。

4　结束语

本文方法最大程度地利用了通信类对象在电磁发射行为上的基本规律，将其行为规律转化为信号分析中的时间性规律，并据此建立模型获得了超额处理增益。实际的通信系统中有载波同步、帧同步和位同步等结构，其中的时间规律信息都将为分析带来巨大的收益。此外，对于时间结构周期具体值的估计误差有随着时间积累的弊端，在后续的研究使用中应考虑加以改进并克服。

[1]秦军振.外辐射源雷达系统的测向及定位算法研究[D].西安：西安电子科技大学，2009：1-4.

[2]侍伟伟，胡文，王艳芳，等.基于压缩观测的解距离模糊算法[J].数据采集与处理，2013，28(4)：38-40.

[3]CALIKOGLU B.Evaluation and Analysis of Array Anteimas for Passive Coherent Loeation(PCL)Systems[R].Thesis of Air Force Institute of Technology，2002.

[4]韩军伟.机载单站无源定位技术研究[D].西安：西安电子科技大学，2015：1-14.

[5]李海静，王立刚.远程空空导弹机弹协同无源定位技术研究[J].现代防御技术，2016，44(1)：16-21.

[6]胡来招.无源定位技术综述[J].电子对抗，2004，8(4)：65-70.

[7]张芹.固定单站无源定位系统的可行性研究[D].成都：电子科技大学，2007：1-4.

[8]占荣辉.基于空频域信息的单站被动目标跟踪算法研究[D].郑州：国防科学技术大学，2007：2-12.

[9]应文，李冬海，胡德秀.一种基于时差变化率的单站无源定位方法[J].指挥信息系统与技术，2011，2(1)：27-48.

[10] 应文，李冬海，胡德秀.基于时差和时差变化率的宽带信号单站无源定位方法[J].电子信息对抗技术，2012，27(2)：14-17.

[11] 李仕云.基于EKF的双站测向/时差联合定位算法[J].无线电通信技术，2015，41(1)：38-40.

[12] KANG C W.A Human Motion Tracking Algorithm Using Adaptive EKF Based on Markov Chain[J].IEEE Sensors Journal，2016，16(24)：8953-8962.

[13] 张恒，张迎春.一种动态时分复用方法及FPGA实现[J].无线电工程，2015，45(6)：85-87.

[14] 王鼎，张刚.一种基于窄带信号多普勒频率测量的运动目标直接定位方法[J].电子学报，2017(3)：591-598.

[15] 田由甲，张冠杰.基于多普勒频率变化率的固定单站定位算法研究[J].无线电通信技术，2016，42(4)：61-64.