精彩课堂 贵在追问
——刍议小学数学课堂追问的策略
2018-04-10浙江乐清市大荆镇第三小学325615
浙江乐清市大荆镇第三小学(325615)
追问是指在学生回答教师所预设的问题之后,教师有目的、有方向地再次提问。追问,是引导学生更为深入地理解学习内容的手段,是课堂教学不可或缺的一种理答行为。有效的课堂追问能激发学生的学习内驱力,促使学生迅速地进入最佳的学习状态,促进学生进行深度思考,从而提升学生的学习效率。纵观小学数学课堂追问,仍存在诸多问题,如频率高、简单化、随意性大、缺乏针对性、问题表面化、缺少思考性等。本文针对不同的课堂教学现象,提出了相应的追问策略。
一、教学现象及对应的追问策略
数学课堂追问要凸显教师的教学机智,这就要求教师根据不同的教学内容和情况找准时机,实施有效追问策略,从而对学生的思维行为做及时的点拨和有效的调控,让追问真正促进学生的发展。对此,笔者分析了各种不同的课堂教学现象,并提出了相应的追问策略。
【现象一】学生回答不出来。
课堂中,经常会遇到这种情况:教师提出一个问题,全班都没人举手回答,或者只有一两个学生举手回答,其余学生不知道怎么回答。究其原因是,数学知识较抽象或者学习难度大,造成学生认知困难。尤其是计算类知识,学生对算理的理解更是难上加难。如教学“80÷2的口算方法”时,学生习惯先算“8÷2=4”,再在4的后面添一个0。可为什么能这样做,学生却回答不出来。可见,学生对算理的理解只是浮于表面,不知其本质。那么如何通过追问让学生对算理有深刻的理解呢?
【追问策略】直观式追问,降低认知难度。
经验表明,学生的智力发展,在很大程度上取决于形象思维到抽象思维的过渡。由形象思维向抽象思维过渡是学生思维发展的必经之路,如何架起形象思维与抽象思维的桥梁,让学生顺利实现思维过渡是教学中需要重点解决的问题。直观式追问,即通过教师的追问,让学生用直观的实例或语言来解释算理、概念、现象等,逐步达到从形象思维向抽象思维过渡的目的。
例如,教学“除数是整十数的口算”一课时,教师提问:“有80面彩旗,每班分20面,可以分给几个班?”学生在计算“80÷20”时一般都是先将两个0抵消,再算8÷2=4。为了让学生更好地理解其算理,教师进行了以下直观式追问。
追问1:为什么可以这样做?对于这样的追问,学生无法用语言来表达,但能找到思考的方向。教师适时结合除法的意义,利用图形和计数器表示算式(如图1),学生可以直观看到:随着珠子的不断移动可以得到多道算式。追问2:算式各不相同,怎么都可以用“8÷2”来算呢?通过计数器上数与形的直观演示,学生发现了“8÷2”的实际意义,深刻理解了算理:虽算式不同,但都是在不同的数位上计算8÷2,所以0可以抵消。
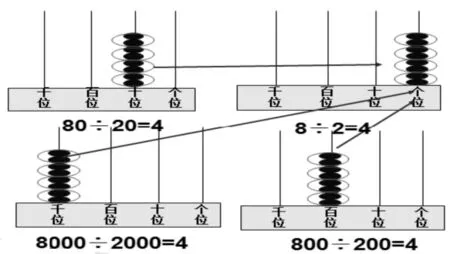
图1
【现象二】学生回答不到点上。
教学中经常存在教师追问后学生总是答不到点上的现象。为什么学生的回答总是停留在表面,不能直指核心呢?究其原因是,教师的追问不到位,学生不理解教师追问的目的。
【追问策略】直线式追问,凸显数学本质。
针对这种现象,教师应进行直线式追问,凸显数学本质。所谓直线式追问,是指沿着一条“主线”逐步深入的追问。直线式追问可以使学生逐步进行思考,从而深刻理解知识的内涵。直线式追问特别适用于重要概念的教学,通过直线式追问可让学生逐步领悟知识的本质内涵。
例如,教学“圆的认识”时,教师在引导学生认识圆心、半径、直径的特征,对圆形成初步认知后,提问:“到底什么是圆呢?”学生根据自身的直观经验对圆的定义进行概括。教师再次追问:“墨子在他的著作中这样描述:‘圆,一中同长也。’你怎么理解这句话?”
从“到底什么是圆?”到“你怎么理解这句话?”,这样设问,让学生从形象直观进入到语言直观,在感受古人语言的精炼之余,更感受到了圆的概论的本质,从而达到圆的概念教学的目的:培养学生的语言概括能力和表达能力。
【现象三】学生回答不全面。
教师提问后,学生可能只回答了其中一点或一个层面,回答得不全面。究其原因是,学生对知识的理解还停留在表面。教材中呈现的概念往往只有一句话的描述,而这一句话却包含了太多层面的东西,太过抽象,学生是难以理解的。教师如果直接讲解概念,学生接受起来比较困难,思维也不缜密,容易以偏概全。
【追问策略】迂回式追问,深化概念建构
在数学教学中,当学生比较、辨析概念有难度时,教师可采用迂回式追问让学生绕到问题的侧面或反面来思考,从而让学生理解概念、掌握本质。迂回式追问可将概念进行分解让学生去分层理解,有效降低了学生的理解难度。
例如,对于“面积”一课,课前教师出示学生前测结果(如图2),暴露学生对面积的真实理解情况,然后再进行以下追问。

图2
师:你觉得什么是面积?
生1:平面图形的大小叫面积。
师:怎么理解平面图形的“大小”?
……
师(出示图3):如果给这个图形涂上颜色,会出现什么情况?
生2:会涂到外面去。
师:那么它有面积吗?如果有,在哪?
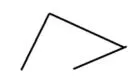
图3
生2(摇头):没有。
师:现在你觉得什么叫面积?
生2:封闭图形的大小叫面积。
师:除了封闭图形有面积,有同学认为数学书的封面也有面积,它的面积在哪里?
……
师:你能用一句话概括什么叫面积吗?
上述教学中,教师不停地追问“你觉得什么是面积?”,一环紧扣一环,使学生在追问中逐渐完善面积的概念。
【现象四】学生回答有偏差。
由于学生年龄较小,生活阅历少,认识问题不全面,对于数学知识的理解容易产生偏差。有时候受旧知的影响,学生也会出现一些知识性错误,阻碍正确认知的形成。此时,教师可通过纠错式追问让学生找到其错误根源,并纠正错误。
【追问策略】纠错式追问,完善知识体系。
在教学中,教师要允许学生出现错误,善待学生的错误,适时引导学生发现自己的错误,再纠正错误。在这环节中,让学生自觉认识到错误所在,知道为什么会产生这样的错误是最困难的。对此,教师可通过纠错式追问,击中要害,从而让学生对所学知识进行全面认识和深刻理解。
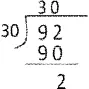
图4
例如,教学“除数是整十数的笔算除法”一课时,教师出示例题“有92本连环画,每班30本,求可以分给几个班?”,学生列出算式“92÷30”后,出现了如图4所示的错误,这是受除数是一位数除法知识迁移影响造成的结果。教师提问:“你怎么知道是错的?错在哪?”学生用“30×30=900”“92里有( )个 30”等方法解释商 3的位置错了。教师的追问:“怎么修改?”在学生回答“要把商写到个位”后,教师再次追问:“为什么要把商写在个位?”结合学生的回答,教师借助多媒体课件展示相关计算过程与方法,让学生直观理解商为什么要写在个位上。最后,教师组织学生比较“92÷3”与“92÷30”,并提问:“92除以3,商3写在十位,为什么92除以30,商却写在个位?”
对错例进行不断的追问,可以让学生直面错误的根源,正视错误的形成原因,从而达到纠错改错的目的。比较问题的教学过程再次让学生感受到错误的原因,从而找到两者的本质区别,加深对知识的理解和掌握。
二、运用追问策略时需要把握的几个度
1.追问的深度
在进行追问时,教师要注意问题的深度,从而通过有深度的追问促进学生思考,使教与学像层层剥笋一样,去粗取精,去伪存真,让所学知识显露无遗地展现在学生的面前,使学生体验到成功的快乐。
2.追问的广度
教师的追问,要让学生触及知识的边缘地带。这样的追问效果就是追问及“边”,也就是追问要达到的广度。“追问及边”是在学生已经掌握了本节课重点的情况下,为了拓展学生的思维而进行的,是对所学知识再学习、再创造的过程。
3.追问的关联度
数学知识具有连贯性,前面知识是后面知识的基础,后面知识是前面知识的发展。教师的追问像线,知识点如珍珠,将散落的珍珠通过线串联,才能将学生引到一定的高度。例如,在教学中教师经常提问:“由此你能想到什么?”就可让学生将新旧知识进行串联、沟通,从而达到认知的新高度。
综上可知,通过追问可让学生对所学知识进行总结、沉淀,让学生的知识成链条状不断发散开,让学生的知识形成一个系统,从而最终达到新的高度。
