数图结合,架起理解的桥梁
——关于“用有余数除法解决按规律排列的问题”的教学思考
2018-04-10浙江象山县丹城第四小学315700
浙江象山县丹城第四小学(315700)
“解决问题”是指综合地、创造性地运用各种数学知识去解决生活中的实际问题和源于数学内部的问题,它渗透在“数与代数”“图形与几何”“统计与概率”“综合与实践”四大领域中。《义务教育数学课程标准(2011年版)》将“解决问题”列为思维总目标之一,它明确指出:增强发现和提出问题的能力、分析和解决问题的能力。由此可见,“解决问题”在小学数学教学中的地位和作用,它既是小学数学教学中的重难点,更是一项基本技能。
在教学中,笔者和很多教师一样,面对众多的“解决问题”而感到痛苦和困惑,故通过“用有余数除法解决按规律排列的问题”一课的磨课过程谈谈对小学第一学段“解决问题”教学的思考。
发现——为何学生依然选择“画一画”
“用有余数除法解决按规律排列的问题”是小学低段(第一学段)众多“解决问题”教学中较为典型的一节课。初读教材之后,笔者很快确定了本节课的教学重点:让学生通过操作、观察,感知余数所表示的基数含义与其相对应的序数之间的联系。为了完成这一教学目标,笔者先给出两个题组,试图让学生在解决问题的过程中,通过对比和观察,感知余数所表示的基数含义与其相对应的序数之间的联系。
题组一:按照下面的规律摆小旗。
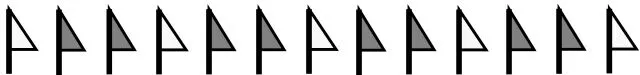
(1)第16面小旗应该是什么颜色?(2)第23面小旗应该是什么颜色?(3)第27面小旗应该是什么颜色?
题组二:按照下面的规律串一串珠子。

(1)第21颗珠子应该是什么颜色?(2)第24颗珠子应该是什么颜色?(3)第30颗珠子应该是什么颜色?
第一步,通过题组一的第(1)题“第16面小旗应该是什么颜色?”,让学生在“尝试解题——反馈交流——呈现方法多样化”的过程中,了解到解决周期问题既可以“画一画、数一数”,也可以用有余数除法来“算一算”。紧接着让学生选择自己喜欢的方法来解决题组一中的第(2)题和第(3)题,学生在解决问题的过程中能体会到用除法解决问题的简便性,并掌握用有余数除法解题的方法。第二步,给出题组二,引导学生用有余数除法解决这三个问题,并巩固“算一算”的方法。第三步,通过观察和比较两个题组中六个问题的解题过程,引导学生得出用余数解决周期问题的一般规律:余数是几,所求数是下一组的第几个;没有余数,所求数是最后一组的最后一个。
自以为以上是完美的教学设计,却在第一次教学尝试中问题频出。于是,笔者对出现的主要问题以及成因进行简单的分析:

课堂上,笔者和选用“画一画”的学生进行了谈话,他们都表示:知道用有余数除法来解决的方法更好,但还是喜欢用“画一画”的方法,因为“画一画”的方法简单。不难看出,这部分学生对用有余数除法的方法不理解,不明白为什么可以用除法解决,以及如何用除法解决,他们与解题组二用“除以3”来列式计算的学生一样,本质上是对“用有余数除法解决按规律排列的问题”方法的不理解。
分析——立足教材与学生,重定重点
基于问题,对症下药,再次研读教材,重新审视教学过程,回顾学生的学习过程,找出教学中的漏洞。
1.研读教材
“用有余数除法解决按规律排列的问题”是人教版教材二年级下册第六单元《有余数的除法》中的内容,本单元的学习内容包括:认识有余数的除法——余数和除数的关系——有余数除法的计算——解决问题(进一法)——解决问题(按规律排列的问题),“用有余数除法解决按规律排列的问题”为本单元的最后一课,看似独立的内容,实则与学生在之前所学习的除法的意义息息相关。

?
从上表可以看出,教材中仅用了一个问题,即“第16面小旗应该是什么颜色?”,通过对这个问题的解决,促使学生亲历解题的全过程,体会解决问题的策略和方法的多样性,理解并掌握“用有余数除法解决按规律排列的问题”的思路和方法。在第一次尝试中,笔者避重就轻,过于注重余数所表示的基数含义与其相对应的序数之间的联系这一规律的得出,而忽略了学生用有余数除法解决例题的思路和方法,尽管有学生提出了可以用除法解决问题,但大部分学生对于如何用除法解决这类问题并不明确,导致不会用有余数除法解决问题。
2.分析学情
课程标准指出:教师教学应该以学生的认知水平和已有的经验为基础。教师只有了解学生的知识储备和已有认知水平,才能让教学更有效。
在学习本节课之前,学生已有经验中与本课息息相关的内容主要有以下两部分:

?
从上表中可以看出,学生学习“用有余数除法解决按规律排列的问题”的知识储备是比较丰富的。但二年级的学生年龄小,理解能力有限,思维还处于形象思维发展的初始阶段,加上“找规律”和“有余数的除法”这两块内容相对独立、互不相干,所以,如何能让学生更好地理解“用有余数除法的知识来解决有规律排列中的数学问题”,是笔者在教学中需要解决的问题。立足教材的编排意图和学生的实际情况,在教学设计整体结构不做改动的情况下,细化新知教学环节的设计,添加动态实物图,促使学生更好地理解“用有余数除法解决按规律排列的问题”的方法,让学生在学习的过程中不再是被动地接受,而是“知其然,更知其所以然”。
细化——化抽象为具体,逐步渗透
【片段一】呈现方法多样性
1.出示问题,收集信息
师(出示PPT):按照下面的规律摆小旗。这样摆下去,第16面小旗应该是什么颜色?

师:说一说,通过读题,你知道了什么?
2.引导学生尝试解决问题
师:能把你的想法记录在探究卡上吗?可以画一画、写一写。
3.汇报交流方法,指名学生展示解题过程
预设一:①画一画(画全部)②画一画(接着画)
师:这两种都是用画一画的方法解题,你更喜欢哪一种方法?为什么?
第13面第16面)
预设二:算一算 :16÷3=5(组)……1(面)
(学生展示算一算的方法,并说一说自己是怎么想的,这个算式表示什么意思)
4.数形结合,理解算式师(PPT动态演示):

(动画演示将16面小旗按照3面为一组进行分组的过程,帮助学生理解16÷3=5(组)……1(面)的含义,及“余1面”表示的含义)

【片段二】优化解题方法
师:第23面小旗应该是什么颜色?第27面小旗应该是什么颜色?(引导学生用自己喜欢的方法解题,让学生在解题过程中感受用“算一算”的方法解题更方便)
师:说说 23÷3=7(组)……2(面)的含义。

师(PPT动态演示):(教师解释27÷3=9(组)的含义)师(PPT动态演示):

【设计意图:本课教学内容中,学生理解的最大难点在于“为什么按规律排列的问题可以用除法解决”和“为什么余数是几就表示下一组的第几个”。基于这两个难点,笔者通过在讲解例题以及练习中引入实物图,并动画演示平均分的过程,帮助学生理解“按规律排列的物体可以按规律进行平均分,除法的实质即为平均分,所以此类问题就可以用除法解决”,并引导学生通过观察实物图得知“余数是几,所求小旗即为下一组的第几个”,从而在余数所表示的基数含义同解题中所需理解的顺数含义之间建立联系。】
教学的成功往往都体现在细节处,在整体设计不变的情况下,只需要在介绍用有余数除法解题的方法时,展示动态的实物图,就能让学生在观察中感知将16面小旗“按每3面为一组,进行平均分”的过程,学生自然而然就会接受用有余数除法解题的方法,不需要教师过多的讲解亦能明白其中的道理。在教学第一学段的众多“解决问题”时,都可以在分析问题和讲解方法时引入图示,根据学生的认知特点,将抽象的问题具体化,并让学生在观察图示的过程中感知用数学方法解题的理由,使教学达到事半功倍的效果。
深思——数图结合,架起理解的桥梁
例如,一年级上册P98的例6:

教师可以引导学生通过“画一画”的方法理解题意,将文字形式的题意用形象的示意图展现出来:
由于受到原有经验的影响,学生看到“剩下”二字,就容易想到减法,在选择运算方法上就产生了困扰。呈现示意图,就能帮助学生通过对图的解读,明白为什么求“原来有多少?”这样的问题要用加法而非减法。
又如,三年级上册P52例3:

“求一个数的几倍是多少”的本质是“求几个几是多少”,对于如何将新知的“求一个数的几倍是多少”与旧知“求几个几是多少”建立联系,教师就可以在教学过程中引入线段图:

通过对线段图的解读,学生很快就理解了“求象棋的价钱,就是求4个8元是多少”,即用乘法计算;通过线段图直观展现了“求一个数的几倍是多少”的数量关系,学生就能联想到乘法的含义,从而理解为什么用乘法解题。
有效的课堂教学应尊重学生的认知发展规律和教材的编排意图,由于学生的思维水平正处于形象思维发展阶段,因此,在低年级教学“解决问题”时,不应过度抽象,可用“图”来解读“数”的形象手段,让数与图有效地结合,这样才能在“实际问题”与“数学方法”之间架起一座助力学生理解的桥梁。
