关注学习过程 促进思维发展
——以“鸡兔同笼”的教学为例
2018-04-10浙江杭州市萧山区新塘小学311200
浙江杭州市萧山区新塘小学(311200)
“鸡兔同笼”是我国古代著名趣题之一。以前,鸡兔同笼问题只是作为小学奥数的常见题型。新课改后,不少版本的教材都新增了一个教学内容——“鸡兔同笼”。人教版教材在六年级上册《数学广角》中详细介绍了“鸡兔同笼”问题的出处、几种典型解法及实际应用,突出“解决问题策略的多样化”。在北师大版教材中,“鸡兔同笼”是作为研究问题的载体,意在让学生经历列表、尝试和不断调整的过程,体会解决问题的一般策略——列表。教材不仅呈现了“鸡兔同笼”的情境和出处,还给出了三个表格,第一张表格是逐一列表法,第二张表格是跳跃列表法,第三张表格是取中列表法。下面就说说如何借助“鸡兔同笼”这一载体,促进学生思维的发展。
一、任务导向,启迪思维
通过课前调查发现,有少数学生在课外就已经接触过“鸡兔同笼”问题,能用假设法解决问题,但大部分学生都没接触过。这样一来,如果让全体学生都用列表法解题,已经学过的学生就会说:“我会用假设法解决问题,多快!何必用列表法。”是呀,为什么一定要用列表法呢?虽然这节课的一个教学目标是让学生学会用“尝试与猜测”解决问题,但是强迫学生用列表法解题,学生只会是为了列表而列表,会失去解题的动力。从大部分学生的学习起点考虑,教学目标“结合解决‘鸡兔同笼’的问题,借助列表法体验尝试与猜测的解题策略”没有错,但面对学习起点不一样的学生,如何预设课堂,才能让每个学生都能主动参与学习,思考问题呢?
分析假设法和列表法,我们不难发现,列表法是先假设鸡或兔的腿数,再一个一个地进行尝试和推算;假设法是先假设全是一种动物,再根据腿数的差距,求出只数。细细想来,假设法也是“先假设——调整——结论”,和列表法是在“做”一样的事,从思维层次上讲:假设法是列表法的一种表现形式,假设法可以看成是对列表法的进一步抽象和提升,而列表法在本质上就是假设法,列表过程的每一步都是假设。
于是,我先让会用假设法解决问题的学生思考问题:“能不能把用假设法解题的过程记录在表格里呢?”学生对这个新任务很感兴趣,在表格里尝试记录假设法解题的思考过程,不敢懈怠(如表1)。接着,让学生介绍自己的方法,解释为什么这么快就能找到正确答案。“80-54=26(条),多了26条腿说明兔子多了13只,也就是鸡要增加13只”。学生在介绍方法的过程中就能感悟到:假设法和列表法这两种方法是有联系的,在列表法中也能找到假设法的影子。

表1
这样的处理方式,既可以调动学生学习的积极性,使他们能够主动地参与课堂学习,也点破了列表法和假设法之间的关系,可谓一举两得。
二、聚焦策略,提升思维
著名的数学教育家波利亚认为:“学习任何知识的最佳途径,都是由自己去发现、探究,因为这种理解最深刻,也最容易掌握其中的内在规律、性质和联系。”因此,教师要有效引导学生经历知识形成的过程,让学生在观察、辨析、判断、分析、抽象、概括等具体的数学活动中积累基本的数学活动经验,提升数学思考的能力。
在引导学生借助表格进行猜测与尝试解决“鸡兔同笼”问题时,除了给出教材上介绍的三种方法“逐一列表法、跳跃列表法、取中列表法”,还可介绍三步列表法(如表2):先假设鸡有1只,再假设鸡有2只,从中发现规律“每增加一只鸡,减少一只兔,腿数会着减少2条。而76比54多了22条腿,所以要增加11只鸡”。
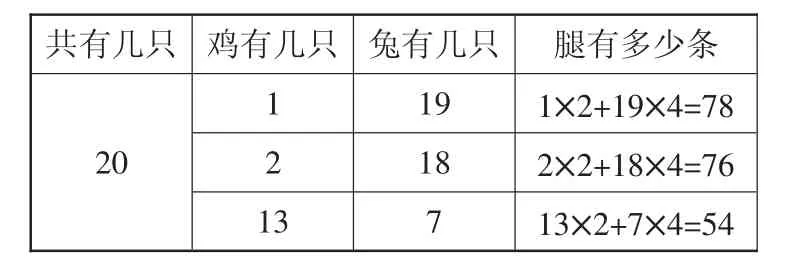
表2
分析这几种列表方式,发现它们的思维含金量是不一样的。逐一列表法是学生一个一个去尝试,学生有没有根据前一次猜测的腿数对鸡和兔的只数进行调整呢?我采访过几位学生,发现他们不是在调整,只是在一个一个地尝试,进行地毯式的搜索,寻找答案;对于跳跃列表法,学生会根据腿数的多少进行调整,相差大,调整的幅度就大些,相差小,调整的幅度就小些,其思维含金量不言而喻——比逐一列表法要高;而取中列表法是学生对题中数据进行分析,再对答案进行估计:可能鸡兔的只数相差不大,所以从中间开始猜测,再进行调整;最后一种是三步列表法,它要求学生利用“每增加一只鸡,减少一只兔,腿数会着减少2只”这个规律,一步调整到位。
在分析学生可能出现的几种思考方法后,我就可以做到有的放矢,由浅入深地组织学生学习。在组织交流逐一列表法时,我引导学生思考:“你是怎么猜测的?”重点观察鸡的只数、兔的只数及相应的腿数的变化规律。在组织交流跳跃列表法时,让学生通过思考“腿数是多了还是少了”“说明了什么”“怎么调整”“为什么调整幅度这么大”“调整幅度怎么变小了”这几个问题,进一步学习“调整”的策略。在组织交流“取中列表法”的过程中,学生就能感悟到:各种方法不是孤立的,要综合运用,才能更快地解决问题。
三、辨析错误,矫正思维
一节课只有40分钟,对于学生的一些错误,教师可以“放大”处理:抛出错误,让学生在讨论和争辩中矫正思维,加深理解。在用列表法解决“鸡兔同笼”问题时,如何根据已有猜测进行调整是教学难点,为了帮助学生把这个内容“踩实”,教师就要及时捕捉学生的错误,把其作为教学资源,引导学生在辨析错误的过程中巩固正确认知。
有位学生给出了如表3所示的方法:在进行第二次猜测“鸡有5只,兔有15只”时,他算出腿有70条,这70条说明腿多了。因此,在进行下一轮猜测时,就应该减少兔的只数,增加鸡的只数,但这位学生还要增加兔的只数,显然,他的调整是不恰当的。
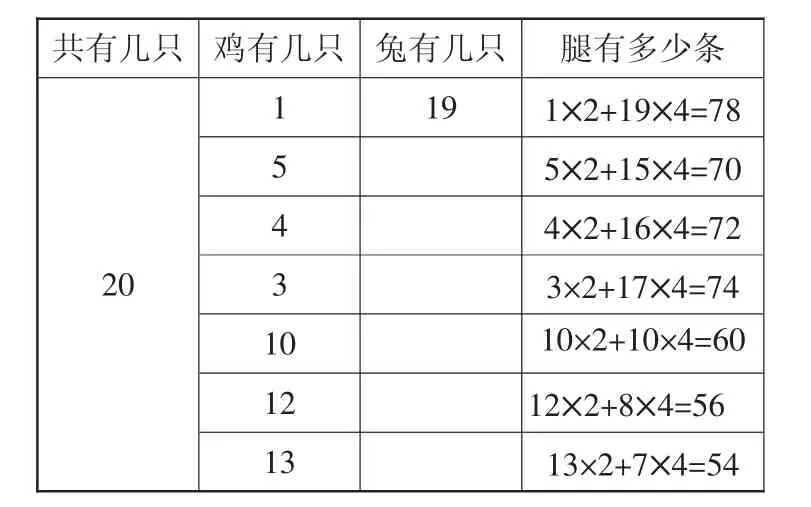
表3
我对这位学生的错误进行了放大处理。“70说明了什么?接着你又假设鸡有4只,兔有16只,为什么这么调整?你是怎么想的?”这样的问题,能让学生深刻认识到:腿多了,说明兔多了,应该要增加鸡的只数,减少兔的只数。
做教师要细心,做数学教师更要细心,要关注到学生解题背后的思考过程“这样的思考过程对不对,这样的思考过程是否简洁”,只有深入分析学生的思考过程,才能纠正学生的错误,才能发展学生的思维。
四、建构模型,拓展思维
一节好的数学课应该让学生懂得一个知识点,获得一种思想,积累一类问题的学习经验,形成简单的数学模型,同时要让学生在应用数学模型过程中,思维品质得到发展,思维能力得到拓展。在学生掌握了列表法之后,教师应从问题出发,提炼出“鸡兔同笼”问题的基本模型,再带领学生将这一简单的数学模型应用到各种问题情境中,完成数学模型的建构与应用。
师:“鸡兔同笼”问题是一个经典的数学问题。在日本也有此类问题的研究,日本人称它为“龟鹤问题”。
师(出示龟鹤问题的图片):日本人说的“龟鹤”和我们说的“鸡兔”有联系吗?
生1:有联系,龟相当于兔,都是四条腿,鹤相当于鸡,都是两条腿。
师:像四条腿和两条腿的,假如不叫它“鸡兔同笼”,也不叫“龟鹤问题”,是否还可以取个其他名字?
生2:人狗问题。
生3:鸭猫问题。
……
师:看来,“鸡兔同笼”可以换成乌龟和仙鹤,人和狗等问题,但归根结底,它们也是“鸡兔同笼”问题。其实“鸡兔同笼”问题只是这一类问题的模型。在生活中也有许多类似于“鸡兔同笼”的问题。
(1)三轮车和自行车共11辆,总共有25个轮子。三轮车和自行车各有多少辆?
(2)乐乐的储蓄罐里有1角和5角的硬币共27枚,总值5.1元,1角和5角的硬币各有多少枚?
师:这些问题和“鸡兔同笼”问题有关联吗?
生4:第(1)题里的自行车相当于2条腿的鸡,三轮车相当3条腿的兔。
生5:第(2)题里的1角相当于鸡,而5角就相当于兔,27枚相当于头数,5.1元相当于腿数。
师:看来,在生活中有很多类似的问题都可以看成是“鸡兔同笼”问题。
在这样一个建构与应用中,学生明白了“鸡兔同笼”问题只是一个简单的“数学模型”,虽然问题的情境在变化,但问题的本质是没有变,学生在解决这些问题的过程中逐渐形成“鸡兔同笼”问题的解题思路和策略。
通过教学“鸡兔同笼”这个内容,我深刻地认识到:教师要为学生的思维发展而教!数学教学是数学思维活动的教学,作为一名数学教师,要把握课堂的每一个细节,寻找行为背后的原因,思考结果背后的过程,为提升学生的思维能力而努力。当然,提高学生的思维能力是一个长期的过程,“冰冻三尺,非一日之寒”,如果能带着“发展学生思维”的理念展开教学,相信我们的数学课堂一定会实现更大的效能!
