激活 积累 提升 应用——以“组合图形的面积计算”为例谈数学基本活动经验的获得

浙江慈溪市实验小学教育集团（315300）

数学基本活动经验是学生在经历数学活动的过程中，产生和形成的感受、体验和感悟。如何让学生获得数学基本活动经验？笔者认为：找准学生的认知起点，为学生激活新经验打下认知和情感的基础；创设有效的数学活动，为学生积累活动经验提供直观性感受；适度地提炼方法，为学生形成新的活动经验给予及时的提升；加强综合性应用，为学生运用新的活动经验提供更为广阔的舞台。

下面以“组合图形的面积计算”的教学为例，试抛教学反思之砖，以引经验分享之玉。

一、找准认知起点，激活经验

杜威曾说：“教育就是经验的改造或重组。”这就是说，一个新知的获得，都是建立在原有的经验基础之上，只有通过经验的改造和重组，才能形成新的数学活动经验。因此，找准学生的认知起点，让原有经验支撑学习活动，才能为学生激活新的活动经验打下认知和情感的基础。

活动一：复习导入，认识组合图形

1.复习学过的平面图形，回顾它们的面积计算方法。

2.出示组合图形（图略），与简单的平面图形进行对比，引出“像这样由简单图形组成的图形就是组合图形。”

图1

3.判断生活中的组合图形（北校区建筑平面示意图），介绍辅助线。

数学具有严密的逻辑性和系统性，学生之前积累的经验，对后续学习有着重要的指导意义。在这一活动中，“复习学过的平面图形，回顾它们的面积计算方法”能唤起学生对已有知识的回忆。活动一虽没有热闹的场面，但却帮助学生对旧知进行了巩固，为学生学习新知打下了扎实的基础。“出示组合图形，并与简单的平面图形进行对比”有效地激活了学生对于组合图形的认知，“判断生活中的组合图形，介绍辅助线”，又为积累“组合图形面积计算”的活动经验起到了指明方向和指导方法的作用。

二、创设有效活动，积累经验

数学基本活动经验的获得离不开有效的数学活动。课程标准指出：数学教学活动，特别是课堂教学，应能激发学生的学习兴趣，调动学生的学习积极性，引发学生的数学思考，鼓励学生的创造性思维。学生应当有足够的时间和空间经历观察、实验、猜测、计算、推理、验证等活动过程。因此，把学生应习得的数学经验融入可操作、能体验的数学活动中，就能为学生积累活动经验提供更多的直观感受。

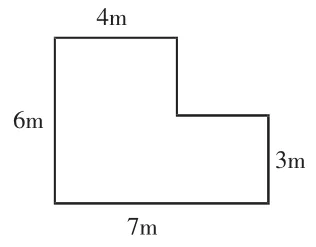
图2

活动二：探索交流，学习组合图形的面积计算

1.创设情境：由图2的绿地铺草皮问题引出如何求组合图形的面积，并揭题。

（5）土的不排水抗剪强度Su与土的破坏模式、土体的非均质性、应变速率和应力历史等有较大关系。根据参数对比，旧路基不排水抗剪强度Su更大。

2.自主探索，交流方法

（1）想：根据老师提供的数据，想一想你准备怎样计算图1的面积。

（2）做：把想到的方法先在图上画一画，再计算。（3）反馈交流方法

图3

为学生创设一个开放的探究空间，能保证每个学生都参与活动，获得直观感受。在这一活动中，重点是对例题进行处理：人教版教材安排的例题是计算房屋侧面积，但学生只能想到分割成一个三角形和一个长方形，以及分割成两个梯形两种解题方法，想法显然不够丰富，如果不能把分割法和添补法整合在一起教学，就无法让学生很好地体验各种方法的优劣。因此，笔者选了北师大版教材的例题，将其调整数据后就作为新课展开的载体，借其相应的丰富的解题方法，拓宽学生的思维，使学生在数学活动的“过程”和“经历”中获得多元的数学活动经验。

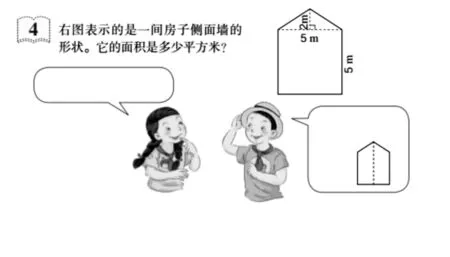
图4（人教版教材）

图5（北师大版教材）

三、适度提炼方法，提升经验

爱因斯坦曾说：“一切关于实在的知识，都是从经验开始，又终结于经验。”这说明：如果仅限于直观感受所获得的经验，这只能算是低级的思维活动。因此，要想使低级的思维活动上升到高级水平，就要适度地对方法进行提炼，引领学生提升所获得的活动经验，使经验从“特殊”推广到“一般”。

活动三：观察对比，方法分类

（1）把组合图形分割成几个简单图形，称为分割法。把分割后的简单图形的面积相加就是组合图形的面积；补上一块的方法称为添补法，可以用求差的方法算出组合图形的面积。

（2）无论是分割法和添补法，目的都是将组合图形转化成已学过的简单图形，所以转化是数学的一种重要的思想方法。

2.优化方法：分割和添补的图形越简单，计算就也越容易。

有效的数学学习应当是以数学思维活动为核心的。在小学数学教学阶段，有意识地引导学生提炼一些基本数学思想方法是提高学生数学能力和思维品质的重要手段，是从传授知识到培养学生分析问题、解决问题能力的重要途径，也是小学数学教学进行素质教育的真正内涵所在。在活动三中，学生丰富和积累了两个方面的数学活动经验：一是认识到分割和添补是两种计算组合图形面积的常用方法；二是运用方法解决问题要灵活多变，要根据问题的特点和提供的信息进行选择。学生获得的新的活动经验具有更广泛的适用性和更高层次的概括性，为解决其他的组合图形面积问题提供一般的解决方法。

四、加强综合应用，运用经验

数学基本活动经验源于数学活动，又应用于现实生活，并会随着学生的实践活动不断丰富、不断发展。因此，加强综合性应用，能为学生运用新经验提供更为广阔的舞台，能引导学生学以致用，提高学生的实践能力。

活动四：巩固练习

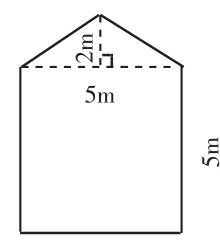
图6

1.基本练习：图6是一间房子的侧面墙。它的面积是多少平方米？

2.提高练习，引导学生发现：

（1）选择用哪种方法来计算组合图形的面积时，不仅要根据图形的特点，还要考虑有没有数据的问题。

（2）计算组合图形的面积不仅可以用分割法、添补法，还可以把分割和添补结合起来，用割补法来求。

（3）在图 7-1、7-2、7-3 中，任选一个图形进行面积的计算。

图7-1

图7-2

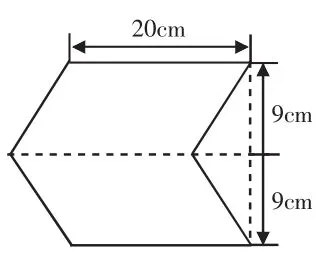
图7-3

3.综合练习：用多种方法解答做一面中队旗要用多少布料。综合运用各种方法解题，并交流反馈。

运用数学活动经验解决实际问题，就能把原本属于认知层面的单一的数学活动经验提高到实践层面的综合性数学活动经验，能有效提升学生的应用意识。在活动四中，有三个层次的练习：

（1）基本练习：计算一间房子侧面墙的面积。训练学生运用分割法解题，同时也引导学生在求组合图形面积时学会正确选择数据。

（2）提高练习：三个组合图形的面积计算。让学生在选择方法计算组合图形的面积的过程中明白，不仅要根据图形的特点选择，还要考虑有没有数据的问题，从而学会灵活运用各种方法求组合图形的面积。

（3）综合练习：计算中队旗的面积。进一步巩固分割法和添补法的运用，引导学生用多种方法求组合图形的面积，培养学生一题多解的能力，以及让学生能够综合运用本节课学到的知识解决问题。

这样，学生不但学会了用基础的方法解题，还能通过拓展延伸的练习，得到了灵活运用各种方法解决实际问题的机会，真正达到运用活动经验的目的。

总之，数学基本活动经验的获得，是学生建构知识体系、形成学科基本素养和能力的重要前提，也是全面提升学生思维水平，促进学生数学思想方法形成的一个重要途径。教师只有不断探索，才能真正找到帮助学生积累数学活动经验的方法，从而培养学生终身受用的数学素养。