例谈计算教学中数学基本活动经验的积累
——以“两位数加两位数的口算”的教学为例
2018-04-10江苏太仓市新区第四小学215400
江苏太仓市新区第四小学(215400)
史宁中教授指出:基本活动经验包括思维的经验和实践的经验。在此基础上,张丹教授进一步将思维的经验细化为相辅相成的两方面:第一,通过数学学习发展一般的思维经验,特别是“从头到尾”发现问题、提出问题、分析问题和解决问题的经验;第二,通过数学学习发展数学思维的经验。
苏教版教材二年级下册的“两位数加两位数的口算”是“数与代数”领域的内容,属于计算教学。那么,如何在计算教学中帮助学生积累数学活动经验呢?下面结合这节课的教学实践,浅谈我的一些想法。
一、激活经验——借助迁移,打开口算思路
在备课之前,对于“学生在面对每一个问题时,他们是如何思考的,其中是否存在经验”,我进行了认真的研究。研究发现:“两位数加两位数的口算”是在学生已经学会两位数加、减整十数或一位数的口算和两位数加减两位数笔算的基础上教学的,学生有相关的经验,所用的口算思路可以是两位数加两位数的笔算,也可以是两位数加整十数再加一位数。由于学生对笔算的思路比较熟悉,所以首先要帮助学生跳出单一的笔算思路,激活学生潜意识中两位数加整十数口算的已有经验,打开学生口算的思路。
课始,我先给出一些两位数加整十数和两位数加一位数的口算题目,初步激活学生已有的经验。
【教学片段1】
师:老师想考考大家的口算能力。
32+2028+1
25+5033+4
48+3028+3
57+2033+9
师:左边这一组都是两位数加整十数,整十数都加在十位上;右边这一组都是两位数加一位数,一位数都加在了个位上。
【教学片段2】
师:下面我们来探索不进位口算“45+23”的方法。
师:“45+23”等于多少呢?
生1:40+20=60,5+3=8,60+8=68。(教师板书)
生2:5+3=8,40+20=60,60+8=68。(教师板书)
生3:把45的十位和个位都给一个1给23,就变成34加34,34加34等于68。
师:生3的方法简单吗?(学生纷纷表示太烦琐)还有其他的口算方法吗?
师:刚才这两种算法都是根据数的组成,把45拆成了40和5,把23拆成了20和3,再来口算。
师:如果只拆一个数,你会口算吗?
生4:把23拆成20和3,先算45+20=65,再算65+3=68。
生5:把45拆成40和5,先算40+23=63,再算63+5=68。
可以看出,有了教学片段1的初步激活,在教学片段2中,我稍微做了一点引导“如果只拆一个数,你会口算吗?”学生马上就想到“同样是先算十位,可以只拆一个数,先用两位数加几个十,再用得数去加几个一”,学生已有的经验得到了有效的激活。
二、经历过程——优化算法,形成口算技能
在倡导算法多样化的同时,教师也要注重算法的优化,但优化的过程不是他人强加的,而是在逐层的练习与对比中体悟出来的,要让学生在发现算法的过程中,在合作与交流中理解和掌握相应的口算方法。
【教学片段3】
师:大家经过思考,得到了四种方法:
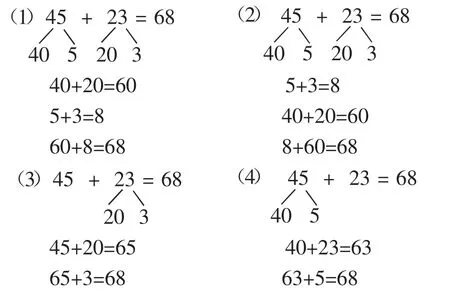
师:比较方法(1)和(2),有没有不同的地方?
生1:方法(1)是从十位上的数算起,方法(2)是从个位上的数算起。
师:口算可以从高位算起。
师:比较方法(1)和(3)的相同点和不同点。
生2:相同点是先加上几个十,都先从十位算起。
生3:不同点是方法(1)是拆两个数,要三道算式。方法(3)是把一个数拆开,先加整十数,再加一位数。这样只要两步口算就好了。
师:比较方法(3)和(4)的相同点和不同点。
生4:不同的地方是方法(3)拆第二个数,方法(4)是拆第一个数。
生5:相同的地方都是先拆一个数,先算加上整十数,再算加上一位数。
在探索算法的过程中,学生给出了多种算法。通过分析各种算法,可以看到它们的共同点:都是利用已经掌握的一位数加一位数、整十数加整十数、整十数加一位数、两位数加一位数等基础性口算,进行两位数加两位数的口算。由于学生对数的分解和组合的理解有差别,导致计算过程以及每一步计算的具体内容不同。因此,教师有必要引导学生分析每一种算法,找到其特点、优点和缺点,引导学生理解算理、优化算法和掌握算法。因此,根据课堂上学生的生成情况,我就设计了相应的三个比较。
总之,有时候,一个好的问题就是一个好的数学活动。数学活动经验是在活动中产生的,因此使学生获得数学活动经验的核心是要提供一个好的活动。在这样的活动中,学生能够经历充分的观察、思考、讨论和比较的过程,获取丰富的感性经验,再从许多数学事实或数学现象中舍去个别的和非本质的属性,抽象出共同的本质属性,从而积累相关的数学活动经验。
三、内化经验——概括反思,培养思维能力
课堂是动态的,教师要适时地引导学生观察、思考、发现、比较,揭示感性经验背后的理性和抽象的数学活动经验。如果学生的思维仅停留于感性认识的层面上,那么他们思考数学问题时就无法摆脱具体和直观的感性经验的束缚,数学抽象思维能力就不能得到培养与发展。
例如,在出示例题情境图后,学生列出了式子,此时,如果教师采取直接告诉学生“先用第一个加数与第二个加数十位上的数相加,再加上第二个加数个位上的数”的方法去算,学生也是能够接受并模仿的,但却失去了一次帮助学生探索抽象算法、体验思维过程、积累活动经验的良好机会。
因此,我安排了四个步骤,引导学生探索两位数加两位数的口算方法:
第一步,利用已有经验来口算,让学生充分交流不同的算法,讨论的目的不仅仅是算出得数,更重要的是让学生借助讨论交流来理解算理。不同的算法体现了学生对数的分解与组合的可行性与合理性的理解,以及思维的连续性和灵活性,在这样的过程中,学生的推理能力可以得到一定程度的发展。
第二步,在比较中优化,分析每一种算法,找到其特点、优点和缺点。在比较和讨论中,学生就会产生简化的心理需要,从而概括和抽象的思维能力得到发展。
第三步,引导学生利用解决第一个问题所获得的经验来解决第二个问题,并把这种“第一个加数去加整十数,再用算得的结果加个位上的数”的算法类推到新的问题的解决中。
第四步,再次引导比较,反思不进位加和进位加的不同思考过程,沟通算法,形成口算方法,从中可以培养学生的反思能力。
四、提升能力——灵活运用,解决实际问题
口算在解决实际问题中用处很大,买玩具的问题,就能让学生学会用口算知识解决实际问题,初步培养学生灵活运用数学活动经验解决问题的能力。
【教学片段4】
师:这节课我们学习了口算,那口算在生活中有什么作用呢?下面我们一起到生活中去看一看。这是一个玩具超市(小飞机25元,小汽车36元,小轮船38元)。
(1)小明:至少带多少钱才能买两件不同的玩具呢?
生1:25+36=61(元)。
师:为什么选择这两个价格的玩具?……
(2)小红:我带了70元买了两样玩具。
师:小朋友们猜一猜,她可能买了哪两件玩具?你是怎么想的?
生2:买小汽车和小轮船。
生(齐):不同意!不同意!
生3:如果是小汽车和小轮船,36+38=74(元),74>70,所以不行。
……
第(1)个问题是基础题,第(2)个问题是开放性问题。这些问题情境非常贴近学生的生活,因为生活中物品的价格也大都是两位数的,那么这种简单的两位数加两位数的口算问题就显得很有价值,也就能够激发学生的学习兴趣,有利于学生体会到口算的应用价值,训练了学生的思维。
总之,从数学活动经验的角度看,学生的学习也正是基于经验而又超越经验,学习数学的过程就是数学活动经验不断激活、提取、调整和提升的过程。本节课中,学生在理解算理的基础上,经历了算法的发现过程,并在合作与交流中理解和掌握比较合理的口算方法,更重要的是,他们在思维活动中体验了算法的形成过程,从而积累数学思维的活动经验。可以说,这是成功的一课。
[参考文献]
[1]史宁中.义务教育数学课程标准(2011版)解读[M].北京:北京师范大学出版社,2012.2.
[2]张丹.发展学生基本活动经验的探索与实践[J].小学数学教师,2014(03).
[3]曹培英.跨越断层,走出误区:数学课程标准核心词的实践解读之六——运算能力(上)[J].小学数学教师,2014(03).
