一种基于光滑L1范数的地震数据插值方法

李　欣　杨　婷　孙文博　王贝贝

(中海油研究总院，北京 100028)

1　引言

受现场采集因素影响，原始地震数据通常不满足采样定理，这会影响去噪、AVO分析、多次波去除以及偏移的效果[1，2]。通过插值处理能得到高密度地震数据[3]，从而减少低频阴影并提高成像精度[4]。目前主流的插值方法都是依托信号处理[1-3，5]，其中基于稀疏变换类方法是假设地震数据在变换域内具有稀疏性，即将地震插值当作稀疏反问题。基于地震信号在空间上的有限带宽性，傅里叶变换和线性拉冬变换可用于恢复不规则数据[1，5-9]。张良等[10]将Shearlet变换应用于地震数据重建。Herrmann 等[11]提出利用曲波变换压缩地震数据，该变换比其他类型变换能更稀疏地表征地震数据。最近，魏小强等[12]将矩阵完备理论用于地震数据插值。Kreimer等[4]提出适用于高维数据插值的张量完备算法。基于稀疏反演的方法需求解不适定性问题，因此可采用稀疏优化法寻找理想解法。随着高维插值方法在地震数据中的推广应用，需探寻针对地震数据处理中大规模问题的快速求解方法。在地震插值方面，Amba等[13]提出求解地震插值的凸集投影(POCS)法。Zwartijes等[14]采用加权迭代最小二乘法解插值问题。Herrmann等[11]把迭代软阈值(IST)法引入地震数据恢复中。Van den Berg等[15]提出稳健的谱梯度投影(SPGL1)方法。Wang等[16]提出L1范数信赖域方法实现地震数据的插值。这些方法都不同程度地改善了插值效果。但随着地震数据量的迅猛增大，亟待研发更快、更稳健的方法以降低CPU时间并获取可靠的插值数据。利用曲波变换[17]，曹静杰等[18]提出基于光滑L0范数的梯度投影地震插值方法，大幅度缩短了运算时间；随后，还提出了基于非凸Lp范数的重建方法并应用于地震反褶积[19]。

在分析、对比各种稀疏优化地震插值方法的时效性和稳健性的基础上，本文选定Huber函数作为L1范数的光滑逼近函数，并构建了快速平滑的L1范数正则化模型，提出了一种快速、稳健的基于Huber函数正则化梯度投影法。文中选择曲波变换作为稀疏变换方法，充分利用其正交性可加快计算速度。数值计算结果证明该方法具有较好的插值结果和较高的计算效率；同时，指出了稀疏优化在地震数据处理中的适用领域。

2　地震数据插值的稀疏优化模型

地震插值可被视为一个反演问题，其对应的正演问题就是地震采集，可写成如下公式

Φx=b

(1)

式中：Φ为采样过程；x为反射系数模型；b为采样数据。由于采样不足，理论上该方程有无数多个解，根据反演理论，可通过一些先验信息获得理想的解。地震同相轴可以通过一些变换稀疏地表示，所以变换域解的稀疏性常常被用作先验信息。地震处理中最常用的就是傅里叶变换[1，14]、线性拉冬变换[9]、抛物线拉冬变换[10]和曲波变换[11]等。近年来，高斯束也被用于地震数据分解[19]。这种先验信息在信号处理中也很常见，如信号压缩与传输、去噪和去卷积[19，20]。如果s=Ψx是稀疏的，其中Ψ是一种变换，那么式(1)可改写成

Φx=ΦΨ*s=As=b

(2)

式中：s是一个以向量表示的离散曲波系数，其稀疏性可用一个拟范数‖s‖0度量，该拟范数表示s的非零元素的个数；A=ΦΨ*，是复合矩阵。于是式(2)即等价为如下优化问题

min‖s‖0s.t.As=b

(3)

上述优化问题的含义是在满足As=b的众多解中，找到最稀疏的那一个解。 然而， ‖s‖0不是一个真

正的范数，它不连续且不可求导。为了能采用凸优化方法求解，该问题一般变为近似凸优化问题求解

min‖s‖1s.t.As=b

(4)

这个问题可通过线性优化和内点法求解，但是计算速度低[21，22]。由于L1范数是不可求导的，所以这类型的问题不能通过共轭梯度法和牛顿型方法直接求解。一种有效的策略是将L1范数替换成光滑的近似函数。因此，式(4)可变成

minF(s)s.t.As=b

(5)

(6)

该函数是光滑的，且当a→0时与|s|非常相似[23]。图1是a=0.0001时的Huber函数形态及其原点局部放大显示(在原点为零)。Huber函数是一个L1和L2的混合范数： 当变量小时表现为L2范数； 当变量大时表现为L1范数。L2范数到L1范数的光滑过度是依靠参数a。Huber函数被广泛地应用于地球物理领域，如讨论线性拟合的鲁棒性问题，但很少应用于解的度量方面。此处将其作为正则化项以得到稀疏的解决方案。

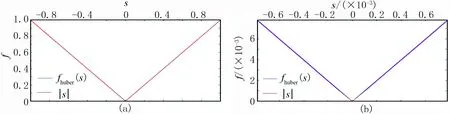
图1　a=0.0001时的Huber函数形态(a)及其局部放大(b)

从上面讨论可知： ①Huber函数中存在一个参数控制其拟合度，且是可微的； ②fhuber(s)在原点等于零，在参数选择合理的情况下fhuber(s)与|s|非常相似，因此它是L1范数的最佳近似。下面给出式(5)的以fhuber(s)为目标函数的表达形式

(7)

根据凸分析理论， {s|As=b}是一个凸集，式(7)可用凸集投影方法求解。作为约束优化问题，投影梯度法是非常有效的一种方法。梯度投影法是最优化算法中解约束优化问题的一类重要方法，它基于目标函数的负梯度方向对迭代解进行初步升级，然后为了防止升级后的解不满足约束条件，通过投影方式将该初步升级后的解投影到约束条件形成的凸集合中，从而实现解的一次完整的升级迭代。这里介绍一种非常快速的投影梯度法求解式(7)，该方法要比目前的方法更节省CPU资源。下面给出求解式(7)的具体步骤。

(1)给出最大迭代次数L、 Huber函数参数a=0.0001和初始迭代次数k=0； 令初始解s0为As=b的L2范数解。

(4)输出最终解s=sk。

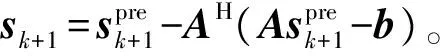
3　曲波变换

基于对地震数据的正交性和优良的稀疏表达能力，本文选择曲波变换作为稀疏变换。傅里叶变换，拉冬类变换和小波变换都可以用来稀疏地表示地震数据，但是对于基于稀疏反演的插值模型来说，要求地震数据在变换域中越稀疏越好，小波变换对地震数据有一定的压缩性，但是其变换后的稀疏性没有曲波变换好。曲波变换作为一个正交、多方向、多尺度、各向异性和局部变换[17]，已被证明是适合地震数据的最稀疏变换[11]之一。另一方面，地震数据的同相轴大多是曲线形状的，傅里叶变换只能稀疏地表示直线形状的同相轴，基于傅里叶变换的地震数据插值需要将地震数据分块，使地震数据在时间和空间窗口中近似为线性的。拉冬类变换存在固有的缺点，首先它们不是严格可逆的，另外对于一些不是规则线性、双曲形状或抛物形状的同相轴，拉冬类变换对地震数据的稀疏表示结果并不理想。因此本文选择存在严格逆变换，并且不需要对地震数据进行分块处理的曲波变换作为稀疏变换，它可以表示成曲波函数φj,k,l(x)与数据f(x)的内积

(8)

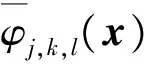
该变换形式可写成s=Ψx，Ψ即是曲波变换。曲波正变换和逆变换的计算成本是O(N2logN)[17]，N表示离散情况下数据的长度。离散的曲波变换是一个紧框架，因此伴随算子Ψ*等价于Ψ的伪逆[19]，形式上，曲波变换的逆可写成x=Ψ*s。

4　数值计算

为了测评本文方法的计算效率，选取两套实际数据进行处理，并与常用的先进稀疏方法做对比。首先给出一个炮集数据实验，第二个实验将进一步测试其对叠后数据的效果。本次选用了三种主流方法来做对比研究。

4.1　炮集数据实验

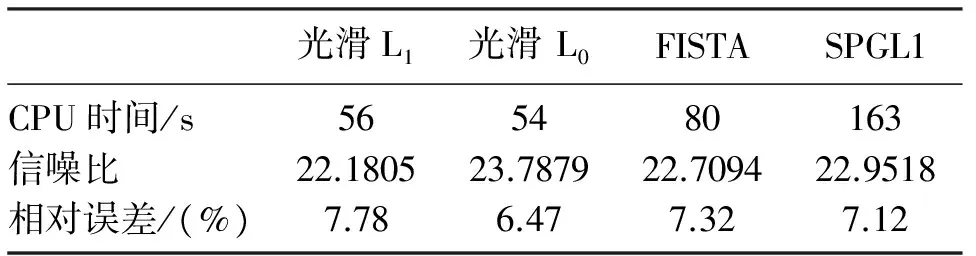
第一个炮数据的接收点间距是25m，采样间隔是2ms。数据包含了115道，每一道有600个采样点，模拟随机的采样 69 道。图2a是原始数据，图2b是采样后的数据。分别利用光滑L1范数方法、光滑L0范数方法[18]、快速迭代阈值法(FISTA)[20]和SPGL1方法[15]进行计算。光滑L1范数方法的最大迭代次数是15次； 光滑L0范数方法有两个循环，每个外部循环次数是2， 内部循环次数是4；FISTA方法最大迭代次数是20； SPGL1方法的最大迭代次数是30。基于这些参数，这些方法将获得相似的插值结果。这些方法的CPU时间、信噪比和相对误差见表1，基于光滑L1范数和光滑L0范数的插值结果见图3，FISTA和SPGL1的插值结果见图4。从结果可以看出，光滑L1范数方法和光滑L0范数方法具有相同的计算速度，都比FIST方法快，约为SPGL1方法的1/3。

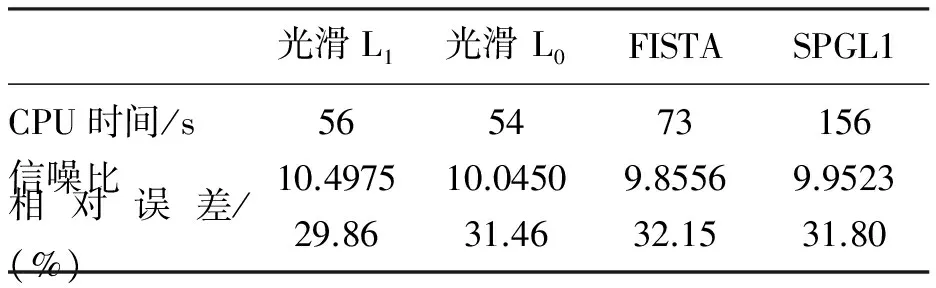
表1　光滑L1、光滑L0、FISTA和SPGL1方法炮集数据对比

图2　原始炮集数据(a)及其重采样数据(b)

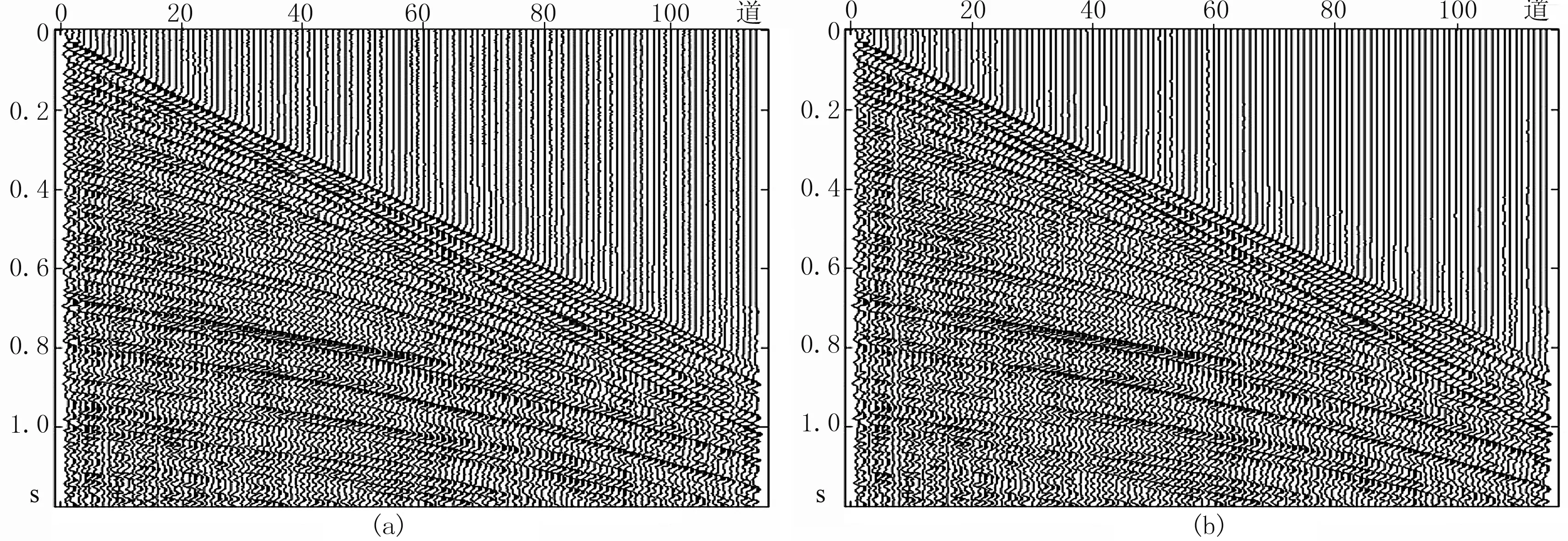
图3　炮集数据的光滑L1方法(a)与光滑L0方法(b)的插值结果

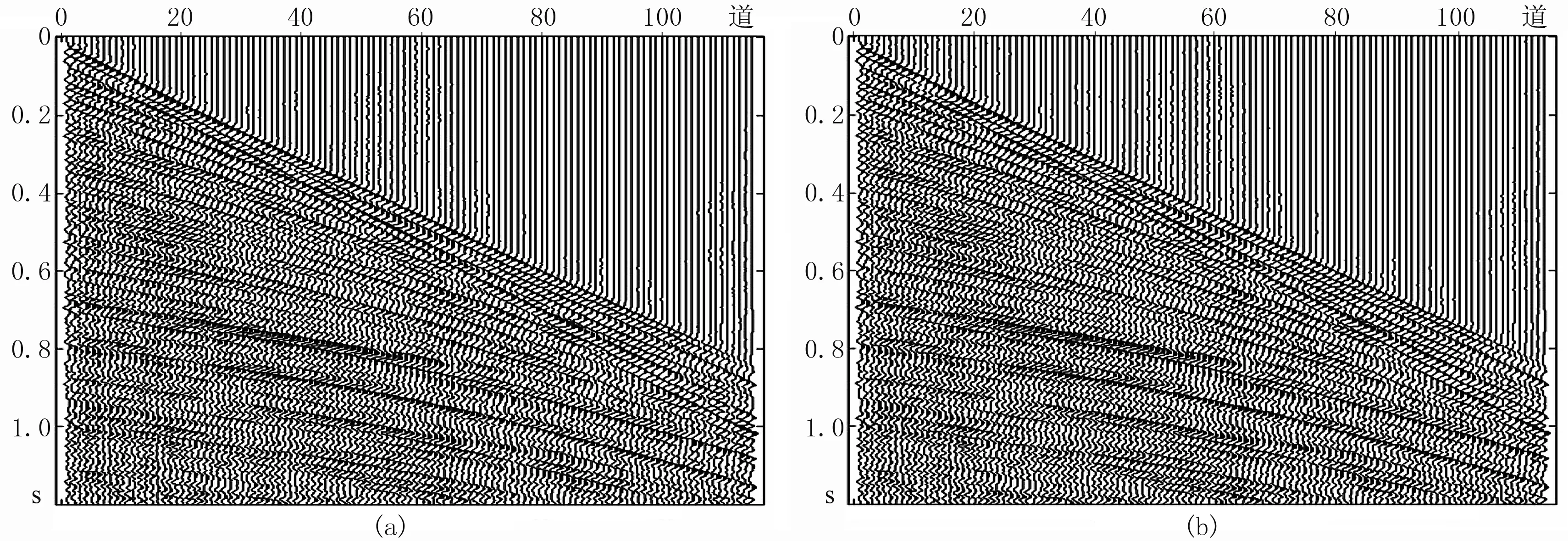
图4　炮集数据的FISTA方法(a)与SPGL1方法(b)的插值结果

4.2　叠加剖面实验

进一步利用叠后数据研究光滑L1范数方法的效率。图5a是一个叠加剖面，包含130道，道间距是25m， 401个时间采样点，时间采样间隔是2ms。不完整采样数据如图5b所示，其中40%的原始数据被随机地去掉。L1范数方法的最大迭代次数是20，图6a是光滑L1范数的插值结果； L0范数的内部循环次数是2，外部循环次数是10，其结果如图6b； FISTA和SPGL1方法的插值结果见图7。这些方法的CPU时间、信噪比和相对误差见表2。与炮集数据实验结果相同，光滑L1范数方法和光滑L0范数方法具有相同的速度，比FISTA方法快，所用时间约为SPGL1方法的1/3，因此本文新方法可显著降低计算成本。由于光滑L0方法是对0范数的近似，而光滑L1方法是对1范数的近似，光滑L0方法能够更加逼近0范数优化问题，因此数值效果要优于光滑L1方法。本文的方法的优越性在于，迭代只需一层循环，需调节的参数比光滑L0方法少，且更易调节，因此本文算法更加简便，容易操作。

图5　原始叠加剖面(a)及其重采样数据(b)

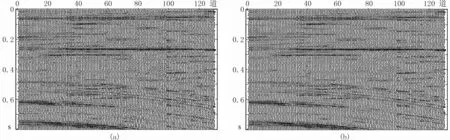
图6　叠加剖面的光滑L1方法(a)与光滑L0方法(b)插值结果

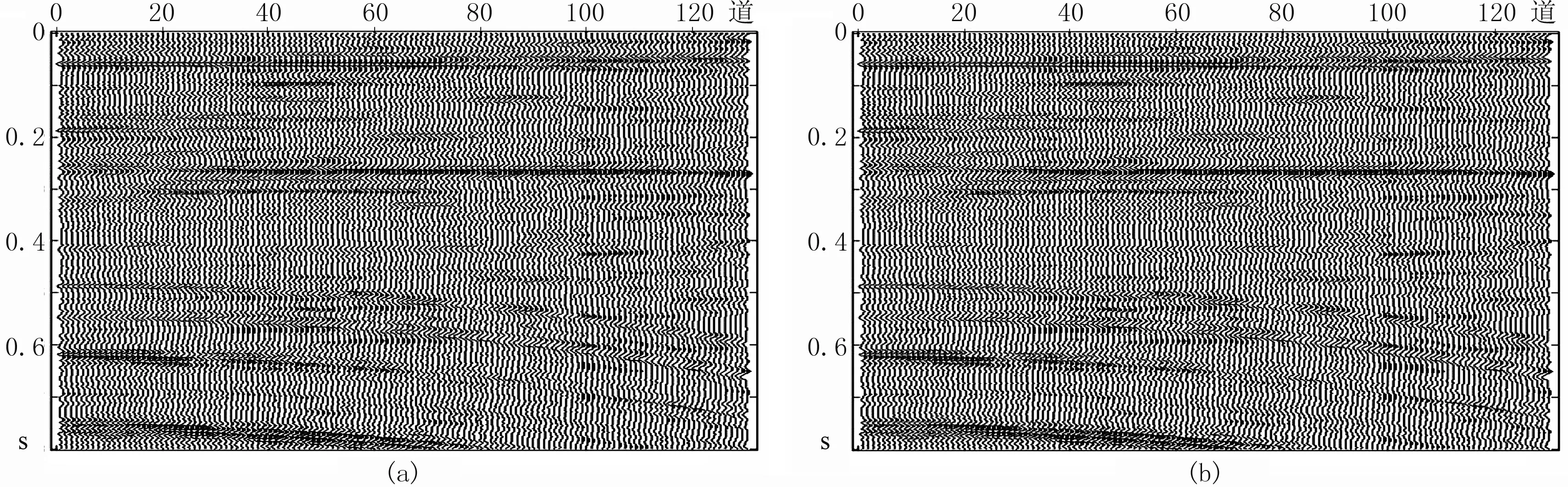
图7　叠加剖面的FISTA方法(a)与SPGL1方法插值结果(b)

光滑L1光滑L0FISTASPGL1CPU时间/s565480163信噪比22．180523．787922．709422．9518相对误差/(%)7．786．477．327．12

5　结论与建议

本文提出采用Huber函数作为目标函数构建地震数据重建反演模型。该函数是一个连续可微的光滑函数，可作为L1范数的近似，因此在求解时能够采用现有的最优化方法求解；针对建立的反演模型提出了一种梯度投影法求解，通过投影方法实现反演模型的快速求解。由于曲波变换能够直接稀疏地表达曲线形状的同相轴，不需要对数据进行分块处理，所以本文采用曲波变换作为稀疏变换，该变换的另一个特点是其正交性可用来加速计算。模拟和真实数据试验证明了本文建立模型和求解方法的有效性；数值结果表明，该新方法比快速迭代软阈值法更快，约为SPGL1方法计算时间的1/3。

随着压缩感知理论的发展，许多稀疏优化模型，稀疏变换和求解方法都可用于地震数据重建问题。L1范数是目前常用的一种的稀疏约束，此外，Lp(0

[1]Liu B.Multi-dimensional Reconstruction of Seismic Data [D].University of Alberta，Edmonton，Canada，2004.

[2]Naghizadeh M，Sacchi M.Beyond alias hierarchical scale curvelet interpolation of regularly and irregularly sampled seismic data.Geophysics，2010，75(6)：WB189-WB202.

[3]Spitz S.Seismic trace interpolation in the F-X domain.Geophysics，1991，56(6)：785-794.

[4]Kreimer N，Edmonton A，Sacchi M.Reconstruction of seismic data via tensor completion.2012 IEEE Statistical Signal Processing Workshop (SSP)，2012，29-32.

[5]Duijndam A，Schonewille M，Hindriks C.Reconstruction of band-limited signals，irregularly sampled along one spatial direction.Geophysics，1999，64(2)：524-538.

[6]王本锋，陈小宏，李景叶等.POCS联合改进的Jitter采样理论曲波域地震数据重建.石油地球物理勘探， 2015，50(1)：20-28.

Wang Benfeng，Chen Xiaohong，Li Jingye et al.Seismic data reconstruction based on POCS and improved Jittered sampling in the curvelet domain.OGP，2015，50(1)：20-28.

[7]Sacchi M，Ulrych T，Walker C.Interpolation and ex-trapolation using a high resolution discrete Fourier transform.IEEE Transactions on Signal Processing，1998，46()：31-38.

[8]Xu S，Zhang Y，Pham D et al.Antileakage Fourier transform for seismic data regularization.Geophysics，2005，70(4):V87-V95.

[9]薛亚茹，唐欢欢，陈小宏.高阶高分辨率Radon变换地震数据重建方法.石油地球物理勘探，2014，49(1)：95-100，131.

Xue Yaru，Tang Huanhuan，Chen Xiaohong.Reconstruction method of seismic data using high-order high resolution Radon transform.OGP，2014，49(1)：95-100，131.

[10]张良，韩立国，徐德鑫等.基于压缩感知技术的Shearlet变换重建地震数据.石油地球物理勘探，2017，52(2)：220-225.

Zhang Liang，Han Liguo，Xu Dexin et al.Reconstruction of seismic data of Shearlet transform based on compressed sensing technology.OGP，2017，52(2)：220-225.

[11]Herrmann F and Hennenfent G.Non-parametric seismic data recovery with curvelet frames.Geophysical Journal International，2008，173(1)：233-248.

[12]魏小强，雷秀丽，马庆珍.基于多道奇异谱分析的三维地震数据规则化方法.石油地球物理勘探，2014，49(5)：846-851.

Wei Xiaoqiang，Lei Xiuli，Ma Qingzhen.3D seismic data regularization based on multi-channel singularspectrum analysis.OGP，2014，49(5)：846-851.

[13]Amba R，Kabir N.3D interpolation of irregular data with a POCS algorithm.Geophysics，2006，71(6)：E91-E97.

[14]Zwartijes P，Sacchi M.Fourier reconstruction of nonuniformly sampled，aliased seismic data.Geophysics，2007，72(1)：V21-V32.

[15]Van den Berg E，Michael F.Probing the pareto frontier for basis pursuit solutions.SIAM Journal on Science Computing，2008，31(2)：890-912.

[16]Wang Y F，Cao J J，Yang C C.Recovery of seismic wavefields based on compressive sensing by a l1-norm constrained trust region method and the piecewise random sub-sampling.Geophysical Journal International，2011，187(1)：199-213.

[17]Candes E.Compressive sampling.Proceedings of In-ternational Congress of Mathematicians，European Mathematical Society Publishing House，Madrid，Spain，2006，33-52.

[18]曹静杰，王彦飞，杨长春.地震数据压缩重构的正则化与零范数稀疏最优化方法.地球物理学报，2012，55(2)：596-607.

Cao Jingjie，Wang Yanfei，Yang Changchun.Seismic data restoration based on compressive sensing using the regularization and zero-norm sparse optimization.Chinese Journal of Geophysics，2012，55(2)：596-607.

[19]曹静杰.基于广义高斯分布和非凸Lp范数正则化的地震稀疏盲反褶积.石油地球物理勘探，2016，51(3)：428-433.

Cao Jingjie.Seismic sparse blind deconvolution based on generalized Gaussian distribution and non-convex Lpnorm regularization.OGP，2016，51(3)：428-433.

[20]Lustig M，Donoho D，Pauly J et al.The application of compressed sensing for rapid MR imaging.Magnetic Resonance on Medicine，2007，58(6)：1182-1195.

[21]Chen S，Donoho D，Saunders M.Atomic decomposi-tion by basis pursuit.Siam Review，2001，43(1)：129-159.

[22]Candes E，Tao T.Decoding by linear programming.IEEE Transactions on Information Theory，2005，51，4203-4215.

[23]Bube K P，NemethT.Fast line searches for the robust solution of linear systems in the hybrid L1/L2 and Huber norms.Geophysics，2007，72(2)：A13-A17.