MOOB：一种改进的基于Bandit模型的推荐算法

帖　军，孙荣苑，孙　翀，郑　禄

(中南民族大学 计算机科学学院，武汉市430074)

目前，向用户呈现个性化内容是在线推荐服务的关键功能之一.在线推荐服务通常实时收集用户的反馈来探索未知信息，以评估新内容受欢迎程度，同时监控其权重的变化.直观地说，系统需要将更多流量分发给新内容，以便更快地了解其价值，减少现有内容的流量跟踪.在此基础上，Bandit模型被广泛应用于推荐系统，逐渐成为推荐领域的研究热点.

Bandit模型，即多臂老虎机模型是一个序列化决策问题[1].每一轮游戏玩家从m个臂中选择一个，并得到相应的回报.玩家的目标是n轮游戏后回报值最大化.

在实际的推荐系统中容易出现长尾现象，不流行的商品会被埋没，用户不易发现新商品.好的推荐系统不仅能够准确预测用户的行为，而且能够扩展用户的视野，帮助用户发现被埋没在长尾中的好商品.Bandit模型虽然能在一定程度上解决此问题，但是Bandit模型将累计遗憾的大小作为衡量算法优劣的唯一指标，在实验过程中容易出现过拟合现象.若将Bandit模型应用于实践，单一的衡量指标显然不能避免长尾现象，无法提高推荐系统覆盖率.

本文围绕上述问题展开研究，基于多臂老虎机模型，提出一种既能使系统得到最大回报，又能提高系统覆盖率的推荐算法.首先，通过用户的历史信息预测出能得到最大回报的物品，然后在推荐物品候选集中进行覆盖率计算，最后得到既能满足用户喜好又能拓展用户兴趣的物品.

1　相关工作

1.1　Bandit模型相关算法

在计算广告和推荐系统领域，Bandit问题也称为EE问题：exploit(开发)-explore(探索)问题.Bandit模型相关算法根据已有的回报选择目前为止回报最高的臂，称之为开发；另一方面，这个目前为止回报最高的臂不一定是最优臂，算法还需选择那些可能回报更高的臂，收集它们的信息，称之为探索，关键是保持开发和探索的平衡，使累计遗憾达到最小[2].如今有许多关于Bandit模型相关算法的研究：

第一类是ε-greedy算法.首先在(0,1)之间选一个较小的数ε；每次以概率ε随机选择一个臂，以1-ε的概率选择估计回报最高的臂.当每个臂都被选择趋近无数次时，回报的估计值逐渐收敛至真实值.文献[3]提出一种新的学习模型，其中ε与实验次数相关.Langford J提出ε-greedy算法是一种上下文有关的Bandit模型算法，在选择时需根据上下文变量进行预估回报值来选择预估回报最大的臂[4].Bouneffouf D等人提出一种算法，该算法将移动上下文感知推荐系统(MCRS)建模为上下文有关的ε-greedy算法[5].

第二类是汤普森采样算法，该算法假设每个臂是否产生收益，其背后有一个概率分布，产生收益的概率为p，通过不断地试验，估计出一个置信度较高的p的概率分布.Chapelle O和Li L证明了汤普森采样算法在广告选择和新闻推荐领域表现良好[6].汤普森采样算法中概率分布多采用贝叶斯概率分布，如文献[7]介绍了一种用于管理多臂老虎机随机概率匹配的启发式算法，该算法观察随机匹配的臂，并选择最佳贝叶斯后验概率的臂.Kawale J等人提出一种在线矩阵分解推荐算法，该算法在一般汤普森采样框架上增加基于Rao-Blackwellized粒子过滤器的在线贝叶斯概率分解方法[8].

第三类是置信区间上界(UCB)算法.UCB算法每次选择前根据已有的实验结果重新估计每个臂的均值和置信区间，最后选择置信区间上限最大的臂.Li L和Chu W等人假设一个臂被选择之后，其获得的回报与相关特征向量成线性关系，并据此提出LinUCB算法.LinUCB算法是一种典型的基于内容的多臂老虎机模型，认为老虎机的臂以特征向量表示且可被观察[9].此后，有很多关于LinUCB算法的研究，例，Bhagat S等人将社交网络关系应用于LinUCB算法以此解决推荐系统中出现的“冷启动”问题[10].Gentile C和 Li S等人将传统的协同过滤算法与LinUCB算法相结合，将用户和商品进行聚类，并根据每次反馈结果调整用户和商品聚类[11,12].

基于内容的Bandit模型是传统老虎机问题的变种.该模型认为回报与环境相关，且将用户和臂的信息用特征向量表示.下面以个性化新闻推荐为例用基于内容的Bandit模型建模，在第t轮时按照以下规则.

(1)算法观察当前用户ut和新闻文章集合At及其特征向量xt,a，其中a∈At.特征向量xt,a包含了用户ut和文章a的信息，称之为上下文.

(2)根据以前获得的反馈，算法选择一篇文章at∈At推荐给用户ut，并获得反馈pt,at，获得的pt,at是由用户ut和文章at共同决定.

(3)算法根据最新得到的反馈，更新下一轮选文章策略.

当t轮推荐结束后计算算法的累计遗憾.算法在选择物品过程中通过每次的结果估算回报，在探索的过程中是有损失的，计算算法的损失值即为累计遗憾.累计遗憾也是衡量Bandit模型算法优劣的唯一指标.其计算的方式为每一次实验的最大回报乘以实验次数减去真实回报.上述例子累计遗憾计算公式为：

(1)

1.2　相关问题

美国杂志主编Chris Anderson在《长尾理论》指出，互联网条件下，冷门商品的销售总额不可忽视，主流商品代表大多数用户的需求，长尾商品代表小部分用户的个性化需求[13].因此，如果通过发掘长尾提高销售额，就必须充分研究用户兴趣，这正是个性化推荐系统的关键问题.

社会学领域存在著名的马太效应，即所谓强者更强，弱者更弱的效应.如果一个系统扩大热门物品和非热门物品之间流行度差距，那该系统会产生马太效应.推荐系统的初衷是挖掘长尾中的物品.为每个用户提供个性化推荐，消除马太效应，使得各种物品都能被展示给对它们感兴趣的人群.

已有的Bandit模型在对用户行为进行预测时以累计遗憾大小为唯一指标，这样容易导致用户只能看到自己目前比较感兴趣的产品，用户可能会感兴趣的商品较少呈现给用户.这样的推荐系统显然不能充分挖掘长尾商品，消除马太效应，为避免此情况的出现，需对现有Bandit模型的相关算法进行改进.

2　算法设计

本文推荐算法的评价指标同时考虑累计遗憾值和物品长尾的发掘能力.在LinUCB算法的基础上进行改进，提出新的推荐算法，并详细介绍算法流程.

2.1　问题描述

在1.1节提到Bandit模型的评价指标即累计遗憾值，根据1.2节对Bandit模型问题的分析，单一的评价指标累计遗憾不能完全衡量算法优劣，要改善这种现状需提出新的评价指标，参数含义如表1所示.

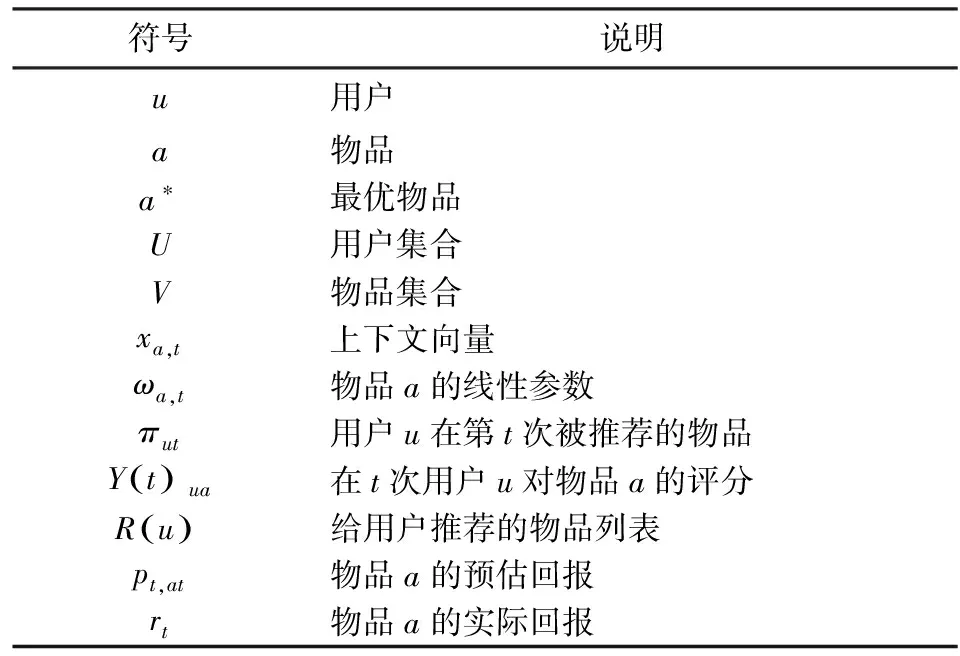
表1　参数含义

覆盖率用来描述一个推荐系统对物品长尾的发掘能力，有不同的定义方法，最简单的定义为推荐的物品占总物品集合的比例.假设系统的用户集合为U，推荐系统给每个用户推荐一个长度为N的物品列表R(u)≜{πu1,…,πut}.推荐系统的覆盖率可通过下面公式计算：

(2)

覆盖率为100%的系统可以有无数的物品流行度分布，如果所有物品都被推荐过，且推荐次数相近，那么物品流行度均匀，推荐系统挖掘长尾能力强.因此可通过研究物品在推荐列表中出现次数的分布描述推荐系统挖掘长尾的能力，在信息论和经济学中有一个著名的指标来描述流行度分布，即基尼系数：

(3)

这里aj是按照物品流行度pop从小到大排序的物品列表中第j个物品.若物品流行度均匀，基尼系数小，若系统物品流行度分配不均，基尼系数大.

为达到推荐系统在保证预测精准度的情况下提高对长尾商品的挖掘能力的目的，需算法保证累计遗憾值和基尼系数达到最小，即选择预测收益最大和基尼系数最小的物品.用公式(4)和公式(5)表示：

(4)

(5)

2.2　MOOB算法

本文在基于内容的Bandit模型的基础上提出了一种新的多目标优化Bandit(MOOB)算法，算法流程图见图1.MOOB算法假设预期估计所获收益与物品的特征向量呈线性相关，沿用2.1的参数，在第t轮为

pt,at=wTa,t-1xa,t.

(6)

(7)

计算得到的pt,at只是一个对所获收益的估计，估计总是不准确的，如能给估计误差一个合理估计，就能控制风险.在选择物品的过程中不仅要选择预估收益大的物品，还要选择预估误差范围大的物品，所以选择物品的方式为：

(8)

算出所有物品的ka,t值之后，对所有的ka,t由大到小排序，取出前K个物品作为候选集，计算候选集中物品的基尼系数，最后选择基尼系数最小的物品推荐给用户，并观察本轮用户对此物品的评分来更新线性关系参数ωa,t.算法1中以伪代码的形式描述了学习算法MOOB.

Algorithm1MOOB(α)Input：α∈R+这个参数决定开发的程度；Init：ba=0∈Rd分析变换的向量；Aa，0=I∈Rd×d逆相关矩阵；a=1，…，m；Output：at推荐给用户的物品fort=1，2，3，…，Tdo　Setωa，t-1=A-1a，t-1ba，t-1，a=1，…，m；　Receiveat∈V，andgetcontextxa，t　forallat∈VdoIfaisnewthenAa←Idba←0d×1endifwa←A-1abapt，at=wTaxa，t+αxTA-1axlogt+1()　endfor　Selecttheitems，whichcorrespondtothetopKlargervaluesinstep10，toformcandidatesetsN　forallat∈NdoGa，t=1n-1∑nj=12j-n-1()rt-1，a　endfor　Chooseat=argmina∈NGa，t，andobserveareal-valuedpayoffrtAa，t←Aat，t-1+xa，txTa，tba，t←ba，t-1+rtxa，tendfor

算法在每次实验时需动态更新Aa,t其所需时间复杂度为O(d2)，而且算法第12步需要选择K个预测回报最大的臂，所以算法在第t次的运算所需时间为O(d2+nlogK).

由算法1中的伪代码和图1算法流程图可知，本文提出的MOOB算法综合考虑了累计遗憾值和基尼系数.在保证用户对推荐结果满意度的基础上能有效避免马太效应.下面将通过对实验结果进行分析来验证算法相关性能.

图1　MOOB算法流程图Fig.1　MOOB algorithm flow chart

3　实验与分析

3.1　实验数据及环境

实验采用YaHoo新闻推荐的数据集完成.该数据集是由“ICML 2012 Exploration and Exploitation 3 Challenge”提取出来.每个用户都由一个136维的二进制特征向量表示，本文把这个特征向量用来表示用户的身份.在去除空用户之后，提取出来8575683条记录分别对应于n=864753个不同的用户.不同的新闻项目的整体数量是5425即m=5425.回报值rt的值为0或1，当登录系统的用户在第t轮点击了某条新闻，则rt=1，若没有点击，则rt=0.通过滤除反馈稀疏的用户，提取出两个数据集一部分作为训练集，一部分作为测试集.在训练集上应用用户兴趣模型，在测试集上进行预测；然后使用累计遗憾值及基尼系数指标评测算法在测试集上的预测结果.

实验采用的硬件环境为Intel(R)Core i5-3470(主频3.20GHz)，RAM为8GB；实验采取的仿真工具为python3.5(matplotlib+numpy+scipy).

3.2　评价指标

为测试本文算法结果，选取了三个常用的性能指标.第一个指标是累计遗憾值，累计遗憾可以对比不同Bandit模型算法的效果；对同一多臂问题用不同Bandit模型算法实验相同次数，观察哪种Bandit模型算法遗憾值增长缓慢，具体计算方法见公式(1).第二个指标是参数预估误差，训练集的绝对误差和测试集的训练误差也是常用的指标之一，很多Bandit模型算法追求遗憾值最小，容易造成过拟合现象.通过对比训练集和测试集的误差来判断算法的过拟合现象是否严重.第三个指标用于衡量推荐结果是否具有马太效应，这里采用基尼系数这一指标，具体计算方法见公式(3).

3.3　实验结果及分析

实验将MOOB算法和一些最先进的LinUCB算法进行比较，主要有以下几种算法：

(1)LinUCB-ONE是UCB算法的单一实例，过去几年在研究界受到了很多关注.LinUCB-ONE在所有用户中分配一个LinUCB的单个实例从而产生对所有用户的相同预测；

(2)LinUCB-IND是一组独立的UCB实例，为每个用户提供完全个性化的推荐；

(3)LinUCB-V也是UCB的单一实例，但是其约束条件更复杂.该算法是“ICML 2012 Exploration and Exploitation 3 Challenge”的赢家.

本次实验抽取40个用户，1000篇文章作为训练集，所有算法的α取值均为0.2.首先，在图2中比较了MOOB算法和LinUCB-ONE、LinUCB-IND、LinUCB-V算法在同样条件下的随着实验迭代次数的增加累计遗憾的变化.

图2　YaHoo数据集上累计遗憾结果比较图Fig.2　Comparison of cumulative regret results on the YaHoo data set

由图2可见，MOOB算法在随着实验次数的增加其累计遗憾值逐渐趋于平稳.由于MOOB算法在考虑累计遗憾的同时考虑了推荐的多样性，所以累计遗憾值略高于LinUCB-V和LinUCB-ONE算法.但是对比和LinUCB-IND算法其累计遗憾值有很大优化.

图3　YaHoo数据集上参数预估误差结果比较图Fig.3　Comparison results of parameter prediction error results on YaHoo data set

由图3可以看到在相同的实验条件下，MOOB算法在所有算法中下降最快并且预估误差最小.同时可以观察到LinUCB-V算法虽然在累计遗憾这一指标上表现良好，但是它的预估误差在四种算法中是最大的，这表示LinUCB-V算法在一定程度上出现了过拟合现象.

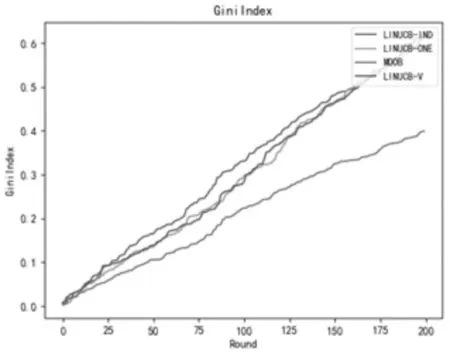
图4　YaHoo数据集上基尼系数结果比较图Fig.4　Comparison of Gini Index Results on YaHoo Data Set

由图4可见四种算法的基尼系数随着实验次数的增加均呈上升趋势.MOOB算法在实验次数较少时其趋势跟其他三种算法差别并不明显，在实验次数达到100之后，其上升趋势明显缓于其他算法.此图也表明：MOOB算法在解决长尾问题上比其他算法更具优势.

4　结语

本文提出的一种基于Bandit模型的推荐算法MOOB，是对传统的LinUCB算法进行改进，使推荐系统的预测准确率和覆盖率都有进一步的改进.通过YaHoo数据集的实验，对所提出算法的性能进行了比较和分析.实验结果表明：MOOB算法能在用户满意度较高的情况下，保证推荐系统物品的流行度较平均，同时有效地避免马太效应，并提高推荐系统对长尾物品的挖掘能力.目前论文没有对用户进行分类研究，下一步研究工作将根据用户的历史行为进行分类，针对不同类别用户使用不同算法进行个性化推荐.

[1]Li L, Chu W, Langford J, et al. Unbiased offline evaluation of contextual-bandit-based news article recommendation algorithms[C]// ACM. International Conference on Web Search and Data Mining.HongKong: ACM, 2011:297-306.

[2]Jones P W. Bandit Problems, Sequential Allocation of Experiments[J]. Journal of the Operational Research Society, 1987, 38(8): 773-774.

[3]Bresler G, Chen G H, Shah D. A Latent Source Model for Online Collaborative Filtering[C]//NIPS. Advances in Neural Information Processing Systems. Montreal: NIPS, 2014: 3347-3355.

[4]Langford J, Zhang T. The epoch-greedy algorithm for multi-armed bandits with side information[C]//NIPS. Advances in Neural Information Processing Systems. Vancouver: NIPS, 2008: 817-824.

[5]Bouneffouf D, Bouzeghoub A, Gançarski A L. Exploration/exploitation trade-off in mobile context-aware recommender systems[C]//IJCAI. Australasian Joint Conference on Artificial Intelligence. Berlin: Springer, 2012: 591-601.

[6]Chapelle O, Li L. An empirical evaluation ofthompson sampling[C]//NIPS. Advances in Neural Information Processing Systems.Granada: NIPS, 2011: 2249-2257.

[7]Scott S L. A modern Bayesian look at the multi‐armed bandit[J]. Applied Stochastic Models in Business and Industry, 2010, 26(6): 639-658.

[8]Kawale J, Bui H H, Kveton B, et al. Efficient Thompson Sampling for Online Matrix-FactorizationRecommendation[C]//NIPS. Advances in Neural Information Processing Systems. Montreal: NIPS, 2015: 1297-1305.

[9]Li L, Chu W, Langford J, et al. A contextual-bandit approach to personalized news article recommendation[C]//ACM.The 19th international conference on World wide web.North Carolina: ACM, 2010: 661-670.

[10]V Caron S, Bhagat S. Mixing bandits: A recipe for improved cold-start recommendations in a social network[C]//ACM. The 7th Workshop on Social Network Mining and Analysis.Chicago: ACM, 2013: 11.

[11]Gentile C, Li S, Zappella G. Online clustering of bandits[C]//ICML. The 31st International Conference on Machine Learning. Beijing: ICML, 2014: 757-765.

[12]Li S, Karatzoglou A, Gentile C. Collaborative filtering bandits[C]//ACM. The 39th International ACM SIGIR conference on Research and Development in Information Retrieval.Pisa: ACM, 2016: 539-548.

[13]Anderson C. The long tail: Why the future of business is selling less of more[M].USA: Hyperion, 2006.