混合配箍混凝土梁最小配箍率分析
2018-04-08屈文俊刘文博
屈文俊,刘文博,庞 蕾
(1. 同济大学土木工程学院,上海 200092; 2. 长安大学建筑工程学院,陕西西安 710061)
0 引 言
混合配筋是基于截面等耐久性设计原理提出的,其基本思想是将耐久性较好的纤维增强复合材料(FRP)筋配置于截面边角部位,而将钢筋配置于截面内部。这种配筋方式可以充分利用FRP筋耐腐蚀性好和钢筋弹性模量高、延性好的优点,具有较好的耐久性能和力学性能,是一种非常理想的配筋方式。混合配箍为将FRP箍筋置于外部,而将钢箍筋置于内部的配筋方法。
对于钢筋混凝土梁的抗剪承载力,目前研究已经比较成熟,相应的计算公式也已经广泛使用。针对FRP配筋混凝土梁的抗剪承载力,各国学者也进行了相应的研究。Shehata等[1]进行了10根FRP箍筋混凝土梁的抗剪承载力试验,研究了包括FRP箍筋锚固能力、锚固长度、最小配筋率、裂缝宽度和抗剪承载力等多个方面,结果表明在满足构造要求的情况下,FRP筋可以发挥极限承载力的50%。Razaqpur等[2]进行了7根无腹筋玻璃纤维复合材料(GFRP)混凝土梁抗剪试验,试验变量仅为配筋率和剪跨比,试验结果显示,梁剪切破坏时纵筋未达到屈服强度,且梁剪切裂缝倾角约为45°。El-sayed等[3]对149根FRP筋混凝土梁试验数据进行了统计,并分别采用各国规范公式进行了验证,研究表明纵筋配筋率可以显著影响FRP混凝土梁的抗剪承载力。师晓权等[4]进行了57根FRP混凝土梁的抗剪试验,结果发现梁破坏时GFRP箍筋的应力仅为75~165 MPa,远没有达到其抗拉强度。除此之外,Machial等[5-8]也进行了FRP混凝土梁的抗剪承载力研究。
虽然目前对钢筋混凝土梁及FRP混凝土梁的抗剪承载力研究已有很多,但对其最小配箍率的研究则相对较少。目前仅部分国家规范规定了FRP箍筋的最小配箍率,对混合配箍梁的最小配箍率则没有相应的计算公式。本文对影响混合配箍最小配筋率的因素进行研究和讨论,提出合理的最小配箍率公式,为工程设计提供技术依据。
1 FRP箍筋梁的抗剪破坏特点及试验验证
1.1 FRP箍筋梁抗剪受力特点
由于FRP筋的低弹性模量和无屈服点特性,使得配置FRP纵筋和箍筋的混凝土梁抗剪性能与普通钢筋混凝土梁有很大区别。
对于普通钢筋,由于其具有屈服平台,故弯曲段的极限承载力与直线段并无差异。Shehata等[1]指出,FRP筋在弯曲过程中其弯曲段强度会显著降低,弯曲段强度一般为直线段的30%~80%。目前美国和日本规范中均考虑了弯曲段强度的折减。
对于有腹筋混凝土梁,其抗剪承载力包括混凝土提供的抗剪承载力和钢筋提供的抗剪承载力。混凝土提供的抗剪承载力与受压区高度密切相关,而受压区高度又与纵筋配置密切相关。对于配置FRP纵筋的混凝土梁,由于纵筋刚度较小,使得梁裂缝宽度较大,受压区高度减小,进而使得抗剪承载力降低。El-sayed等[9]通过试验发现,提高FRP纵筋的配筋率有助于提高FRP混凝土梁的抗剪性能。
配置FRP箍筋的混凝土梁破坏形态通常有2种[10]:一种为FRP箍筋断裂破坏,另一种为混凝土压碎破坏,后者破坏时变形能力略大于前者。无论何种破坏模式,达到极限承载力后继续变形能力均较小,即FRP箍筋梁在极限荷载下破坏较为突然。
1.2 混合配箍梁抗剪破坏特点及试验验证
为了研究混合配箍梁在最小配箍率下的破坏形态,以及确定破坏时FRP箍筋的应变范围,本文进行了9根钢-GFRP混合配箍梁的抗剪试验。试验的主要变量包括钢纵筋和GFRP纵筋配筋量、剪跨比、箍筋配筋形式。
1.2.1试验概况
所有试件截面宽度b=300 mm,截面高度h=350 mm,有效高度h0=315 mm,试件全长L=2 900 mm,试验时梁两端各留出250 mm长度以防止纵筋从端部拔出,实际加载跨度为2 400 mm。试件加载如图1所示,其中P为荷载。试件主要参数见表1,Asl为钢纵筋截面面积,Afl为FRP纵筋截面面积,Asv为钢箍筋截面面积,Afv为FRP箍筋截面面积,ρdev,l,ρdev分别为按等刚度原则计算的等效纵筋配筋率和等效箍筋配筋率。ρdev,l,ρdev具体计算公式为
(1)
式中:Ef,Es分别为FRP筋和钢筋的弹性模量。
试验在门式反力架上进行,采用两点加载方式(其中梁试验SG-007A-3.5/4.5-GS2为单点加载),使用液压千斤顶对试件施加竖向荷载。
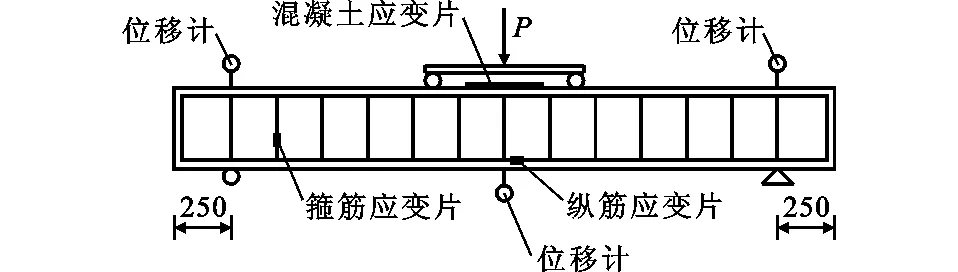
图1 试件加载(单位:mm)Fig.1 Loading of Specimens (Unit:mm)

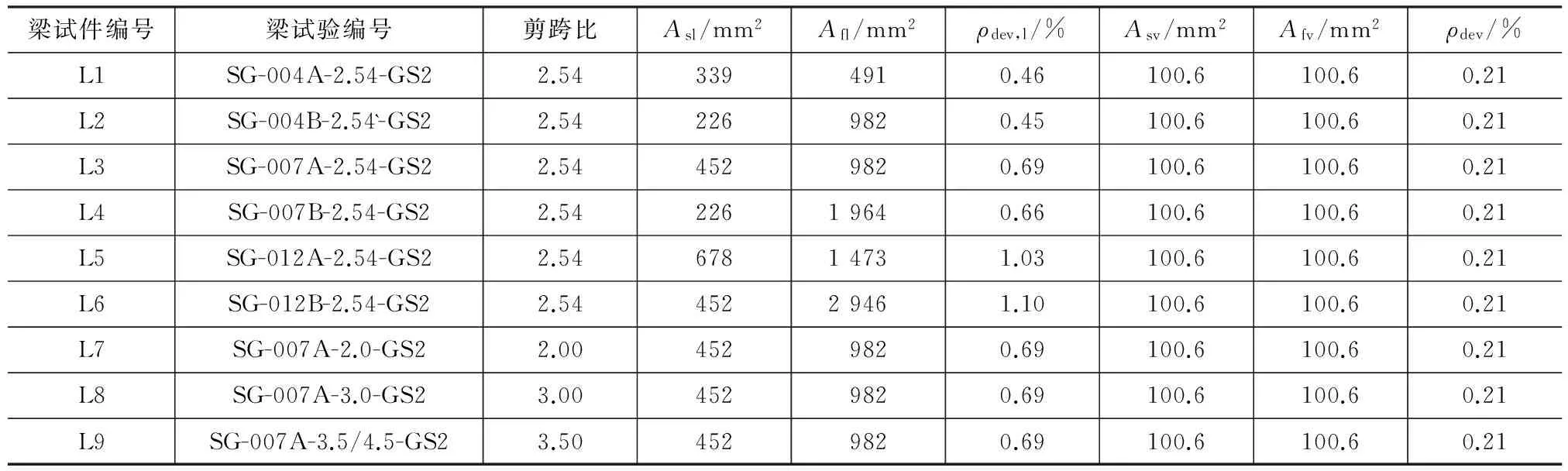
表1 试件主要参数Tab.1 Main Parameters of Specimens
1.2.2试验过程
试验梁在正式加载前均先进行预加载,确认各仪表及应变片读数是否正常,同时保证加载面与梁紧密接触。
各试验梁的加载-破坏现象基本类似:当截面剪力达到30~40 kN时,梁底出现第1条裂缝;此后裂缝不断发展,形成剪切斜裂缝;之后梁腹部形成腹剪斜裂缝,并逐渐向支座处延伸;最终斜裂缝贯通加载点和支座,剪压区混凝土被压碎,梁受剪破坏。梁破坏情况见图2,3。

图2 L1破坏情况Fig.2 Failure Mode of L1

图3 L2破坏情况Fig.3 Failure Mode of L2
1.2.3试验结果
通过对试验梁箍筋的应变分析发现,当梁发生剪切破坏时,GFRP箍筋的应变可以达到0.007以上,钢箍筋达到屈服强度;当斜裂缝达到0.15 mm时,FRP筋的应变达到0.005以上。这说明在最小配箍率下,混合配箍混凝土梁的FRP筋可以达到较大的应变值。
本文试验中所有梁均为剪切破坏,破坏模式类似于钢筋混凝土梁的剪压破坏:试件两侧裂缝不断发展,当临界斜裂缝形成时,与之相交的箍筋依次达到屈服,期间纵筋也达到屈服,最后上部混凝土压碎,试件剪切破坏。极限荷载作用下混合配筋混凝土梁的变形较钢筋混凝土梁大,表明混合配筋混凝土梁具有变形量较大的特点。
2 配筋梁最小配箍率的定义及研究
2.1 各国规范对钢筋混凝土梁最小配箍率的定义
钢筋混凝土梁最小配箍率的定义为同时发生梁抗剪开裂与箍筋达到屈服强度时的配箍率。尽管各国规范对钢筋混凝土梁最小配箍率进行限定时均沿用该基本概念,但计算公式各有不同。
中国《混凝土结构设计规范》(GB 50010—2010)[11]中对抗剪最小配箍率ρsv,min的限值定义如下
(2)
式中:ft为混凝土抗拉强度;fyv为箍筋屈服强度。
中国规范计算最小配箍率时采用了混凝土抗拉强度,其表达式中的参数0.24根据试验资料及实际经验得到。
美国ACI 318-11[12]规范中对抗剪最小配箍截面面积Asv,min的限值规定如下
(3)
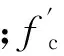
美国规范较独特地采用了公式和最小值限值的双重控制方法,其表达式是建立在经验基础上的。除表达式与中国规范不同外,美国规范的最小配箍率设置条件为Vu0.5φVc(Vu为截面设计抗剪承载力,Vc为相应无腹筋梁抗剪承载力,φ为混凝土抗力分项系数),而中国规范则为VuVc。
加拿大CSA A23.3-04[13]规范中对抗剪最小配箍截面面积Asv,min的限值规定如下
(4)
加拿大规范最小配箍率在抗震情况下的要求与非抗震相同,且公式(4)中的箍筋截面面积包含抗扭箍筋截面面积。
日本JSCE-2007[14]规范中取抗剪最小配箍率为0.15%。日本规范最小配箍率是考虑到没有配置抗剪钢筋的构件中斜裂缝经常发生而设置的。日本规范限值是较为简单的经验值,其他问题通过对钢筋间距和直径的要求来保证。
2.2 混合配箍混凝土梁最小配箍率的定义
由试验可知,梁出现斜裂缝前,箍筋应力均较小,即筋材均处于线弹性状态,同时梁抗剪破坏时钢箍筋屈服先于FRP箍筋破坏[15]。因此,混合配箍混凝土梁中可以将FRP筋截面面积按弹性模量等效为钢筋截面面积,配箍率ρdev定义为
(5)
式中:asv,afv分别为单肢钢箍筋和FRP箍筋截面面积;ns,nf分别为钢箍筋和FRP箍筋肢数;αE=Ef/Es;sv,sf分别为钢筋和FRP箍筋间距。
对纯FRP箍筋的混凝土梁,由于FRP筋无名义屈服强度,且抗剪破坏时箍筋远不会达到极限承载力,故最小配箍率定义为梁出现抗剪斜裂缝时箍筋恰好达到某个应力或应变限值的配箍率。主要问题在于如何确定FRP箍筋在抗剪极限状态下的应变限值。目前美国和加拿大的FRP混凝土计算规范对FRP箍筋的应变限值为0.004,日本规范则限制FRP筋应力不超过弯曲段抗拉强度。由于本文讨论的是最小配箍率,其对应的是开裂荷载等于极限承载力的情况。在本文试验中,极限承载力下箍筋应变为0.005以上,其他学者的试验结果则为0.002 0~0.003 5[1,16],故混合配箍梁的最小配箍率ρv,min定义为梁出现抗剪斜裂缝时FRP筋应变恰好达到0.003时的配箍率,在该应变下通常钢筋已经屈服。
3 混合配箍梁最小配箍率的分析
为了与中国现有规范保持一致,根据式(5)的定义,混合配箍梁的最小配箍率限值为
(6)
式中:fsv为钢筋屈服强度;αv为系数,对钢筋混凝土梁,参照中国规范,αv=0.24,对FRP配箍梁及混合配箍梁,αv通过分析确定。
ACI规范已经指出,对FRP混凝土梁,纵筋刚度会显著影响梁的抗剪承载力,因此本文分析时将主要考虑纵筋刚度的影响,以式(6)为基础进行推导,确定系数αv的取值。
中国《混凝土结构设计规范》(GB 50010—2010)[11]中受弯构件抗剪承载力Vv计算公式为
(7)
式(7)中的0.7ftbh0为混凝土提供的抗剪承载力,由于纵筋刚度会显著影响混凝土提供的抗剪承载力,因此有必要对最小配箍率下混凝土提供的抗剪承载力比例进行推导计算。
混凝土提供的抗剪承载力与总抗剪承载力的比值Rc-s为
(8)
中国规范中箍筋最小配筋率限值为0.24ft/fsv,代入式(8)得Rc-s=0.745。
对于最小配箍率的混凝土梁,名义上混凝土所占抗力比值为0.745,当配箍率大于最小配箍率时,由公式(8)可知混凝土所占承载力比例下降,因此取比值0.745是较为保守的。
对于纵筋刚度对混凝土提供的承载力影响,本文将根据美国规范推导。
美国现行规范[17]中对FRP混凝土梁的抗剪承载力计算规定如下
(9)
Vfv=ρfvffvbh0
(10)
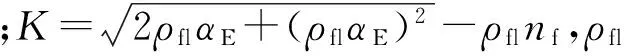
美国现行钢筋混凝土计算规范[12]中对梁的抗剪承载力规定如下
(11)
(12)
式中:Vsv为钢纵筋提供的抗剪承载力。
定义系数φc为相同纵筋配筋率下FRP纵筋混凝土梁与钢纵筋混凝土梁中Vc的比值,即
(13)
当配箍率恰好为最小配箍率时,FRP纵筋混凝土梁的抗剪折减系数c为
c=0.745φc+0.255
(14)
系数c的物理意义为当箍筋配筋形式相同且ρv等于钢筋混凝土梁的ρv,min时,相同纵筋截面面积的FRP纵筋梁与钢纵筋梁的抗剪承载力比值。c与纵筋配筋率ρl的关系见图4(AFRP为芳纶纤维增强塑料)。
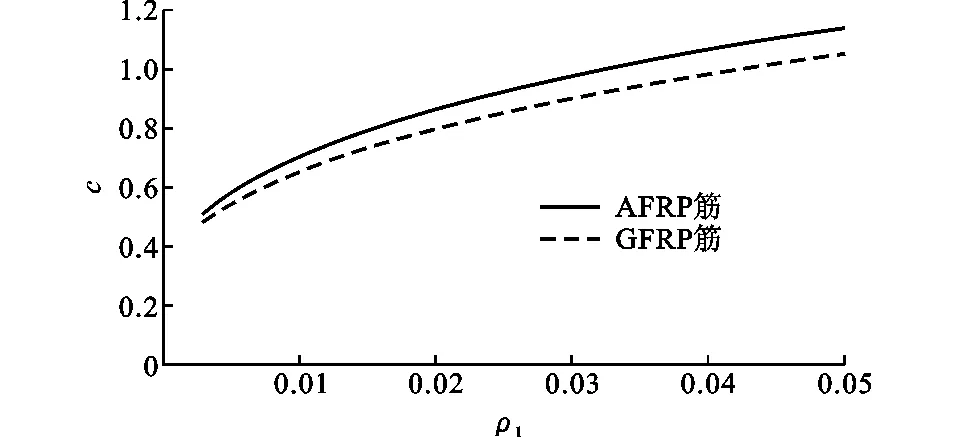
图4c与ρl的关系Fig.4 Relationship Between c and ρl
由于c与ρl为非线性关系,为计算方便,偏保守地将其小于1的部分变换为直线。对目前常用的HRB400纵筋,混凝土抗压强度取C50时,纵筋最小配筋率ρmin,HRB400为0.002 4。
等刚度原则对应的GFRP,AFRP纵筋最小配筋率ρmin,GFRP,ρmin,AFRP分别为0.009 6和0.007 4。
当FRP纵筋配筋率大于ρmin,GFRP,ρmin,AFRP的计算值时,其等效刚度大于钢筋混凝土梁纵筋最小配筋率时的刚度,此时可认为纵筋刚度对混凝土提供的抗剪承载力影响较小,可忽略不计。当纵筋配筋率小于ρmin,GFRP,ρmin,AFRP的计算值时,认为纵筋刚度会影响抗剪承载力,此时需对混凝土提供的抗剪承载力进行折减。
由于FRP箍筋受力时应变不均匀[4],故取2倍ρmin,GFRP,ρmin,AFRP值作为折减配筋率的上限值,同时取配筋率0.004作为折减配筋率的下限值,对c值进行直线化简。
对于GFRP,有
c=33ρfl+0.38
(15)
对于AFRP,有
c=41ρfl+0.39
(16)
式中:c1时取c=1。
由于混凝土、钢筋和FRP筋在开裂前均为线弹性,因此可运用叠加原理,将混凝土部分的抗剪承载力分解为两部分:一部分由混凝土和钢筋组成的梁提供,另一部分由混凝土和FRP纵筋组成的梁提供。这两部分中,由FRP部分提供的混凝土抗力需进行折减,折减系数按全部纵筋截面面积计算。
以上两部分抗力按钢筋和FRP筋的纵向刚度分配,分配系数如下
(17)
(18)
式中:Rs,Rf分别为钢筋和FRP筋所占刚度比例。
综合式(15)~(18),可得出混合配箍混凝土梁最小配箍率计算公式为
(19)
式中:α为放大系数。
对配置钢箍筋和同时配置FRP箍筋和钢箍筋的混凝土梁,fyv取钢筋屈服强度;对仅配置FRP箍筋的梁,可偏安全地取fyv=300 MPa。α按式(20)计算,即
(20)
计算c值时配筋率ρfl应按全部受拉纵筋截面面积计算。
以上仅进行了GFRP筋和AFRP筋的推导,对于CFRP筋,由于其弹性模量相对较大(约为1.5×105MPa),与钢筋的弹性模量较为接近,故采用CFRP纵筋时可不考虑纵筋刚度对抗剪承载力的影响。
4 简化公式
式(19),(20)虽然给出了计算混合配箍梁最小配箍率的理论公式,但该公式形式复杂,参数较多,不方便工程人员使用,现对其进行简化。
对不同纵筋配筋率和不同FRP所占刚度比下的α进行计算,此处偏保守地以GFRP进行计算,结果见表2。
依据表2中的数据,偏安全地进行线性简化,得到α的简化计算公式为
α=1+0.6Rf
(21)
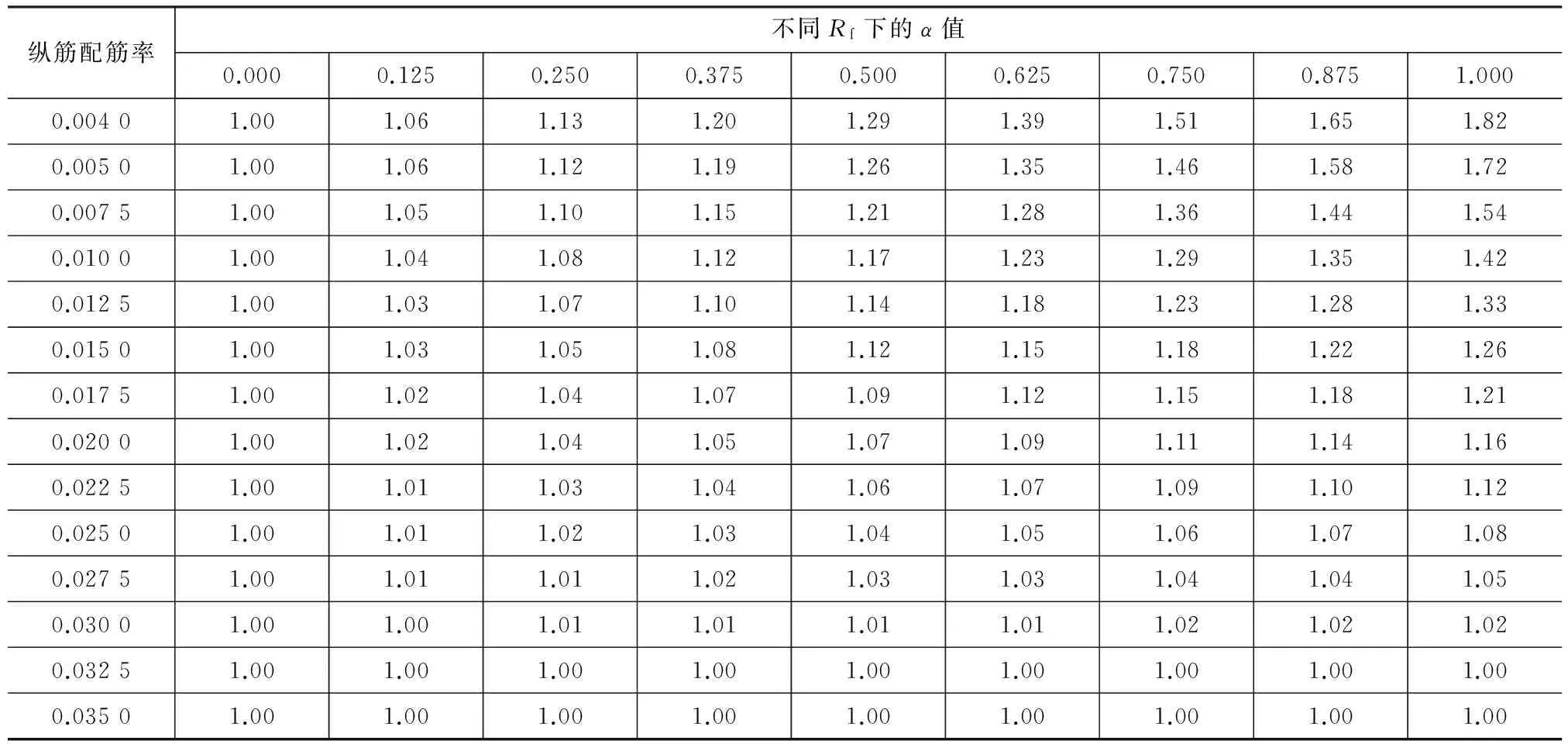
表2 不同配筋率下α计算结果Tab.2 Calculation Results of α Under Different Reinforcement Ratios
表2中数据仅对工程上很少出现的纵筋配筋率很低的情况不满足(约占2.4%),因此式(21)的简化计算结果在工程上是可以接受的。
横向抗剪最小配箍率ρdev的计算公式为
(22)
对于仅配置FRP箍筋的梁,可以偏安全地取fyv=300 MPa。
5 结语
(1)进行了9根混合配筋混凝土梁的抗剪试验,研究了混合配箍梁的抗剪破坏形态及FRP箍筋的应变范围。试验表明混合配箍梁的抗剪破坏模式类似于钢筋混凝土梁的抗剪破坏模式,斜裂缝宽度为0.15 mm时,FRP箍筋应变可达0.005。
(2)提出了混合配箍混凝土梁配箍率的计算方法,给出了混合配箍混凝土梁最小配箍率的定义。根据美国ACI规范及中国钢筋混凝土规范,推导了混合配箍梁的最小配箍率限值计算公式。依据试验结果,给出了混合配箍梁最小配箍率的简化计算公式,该公式适用于所有配箍梁。
参考文献:
[1]SHEHATA E,MORPHY R,RIZKALLA S.Fibre Reinforced Polymer Shear Reinforcement for Concrete Members:Behaviour and Design Guidelines[J].Canadian Journal of Civil Engineering,2000,27(5):859-872.
[2]RAZAQPUR A G,ISGOR B O,GREENAWAY S,et al.Concrete Contribution to the Shear Resistance of Fiber Reinforced Polymer Reinforced Concrete Members[J].Journal of Composites for Construction,2004,8(5):452-460.
[3]EL-SAYED A K,SOUDKI K.Evaluation of Shear Design Equations of Concrete Beams with FRP Reinforcement[J].Journal of Composites for Construction,2011,15(1):9-20.
[4]师晓权,张志强,李志业,等.GFRP筋混凝土梁抗剪承载力影响因素[J].西南交通大学学报,2010,45(6):898-903,913.
SHI Xiao-quan,ZHANG Zhi-qiang,LI Zhi-ye,et al.Influencing Factors of Shear Capacity of Concrete Beam Reinforced with GFRP[J].Journal of Southwest Jiaotong University,2010,45(6):898-903,913.
[5]MACHIAL R,ALAM M S,RTEIL A.Revisiting the Shear Design Equations for Concrete Beams Reinforced with FRP Rebar and Stirrup[J].Materials and Structures,2012,45(11):1593-1612.
[6]NEHDI M,CHABIB H E,SAID A A.Proposed Shear Design Equations for FRP-reinforced Concrete Beams Based on Genetic Algorithms Approach[J].Journal of Materials in Civil Engineering,2007,19(12):1033-1042.
[7]李炳宏,江世永,石钱华,等.BFRP连续螺旋箍筋混凝土梁抗剪性能试验研究[J].后勤工程学院学报,2011,27(1):1-6.
LI Bing-hong,JIANG Shi-yong,SHI Qian-hua,et al.Experimental Study on Shear Behavior of Concrete Beams Reinforced with Continuous BFRP Rectangular Spirals[J].Journal of Logistical Engineering University,2011,27(1):1-6.
[8]张晓亮,屈文俊.无腹筋GFRP筋混凝土梁抗剪性能试验[J].中国公路学报,2010,23(5):51-57.
ZHANG Xiao-liang,QU Wen-jun.Shear Behavior Test of GFRP-reinforced Concrete Beams Without Stirrups[J].China Journal of Highway and Transport,2010,23(5):51-57.
[9]EL-SAYED A,EL-SALAKAWY E,BENMOKRA-NE B.Shear Strength of One-way Concrete Slabs Reinforced with Fiber-reinforced Polymer Composite Bars[J].Journal of Composites for Construction,2005,9(2):147-157.
[10]AHMED E A,EL-SAYED A K,EL-SALAKAWY E,et al.Bend Strength of FRP Stirrups:Comparison and Evaluation of Testing Methods[J].Journal of Composites for Construction,2010,14(1):3-10.
[11]GB 50010—2010,混凝土结构设计规范[S].
GB 50010—2010,Code for Design of Concrete Structures[S].
[12]ACI 318-11,Building Code Requirements for Structural Concrete[S].
[13]CSA A23.3-04,Design of Concrete Structures[S].
[14]JSCE-2007,Standard Specifications for Concrete Structures[S].
[15]梁志强.混杂配筋混凝土梁抗剪性能研究[D].上海:同济大学,2007.
LIANG Zhi-qiang.Research on the Shear Behavior of Hybrid Reinforced Concrete Beams[D].Shanghai:Tongji University,2007.
[16]EL-SAYED A,EL-SALAKAWY E,BENMOKRA-NE B.Mechanical and Structural Characterization of New Carbon FRP Stirrups for Concrete Members[J].Journal of Composites for Construction,2007,11(4):352-362.
[17]ACI 440.1R-06,Guide for the Design and Construction of Concrete Reinforced with FRP Bars[S].
