济南典型地层基坑空间效应规律研究

李连祥，成晓阳，黄佳佳，胡　峰

(1. 山东大学基坑与深基础工程技术研究中心，山东济南　250061； 2. 山东大学土建与水利学院，山东济南　250061)

0　引　言

近年来，基坑工程向深大长方向发展，平面形状趋于复杂，很多基坑涉及阳角、坑中坑，空间效应愈发显著[1]。由于空间效应使结构受力复杂化，忽略空间效应可能会造成成本增加甚至安全事故的发生。例如新加坡Nicoll地铁基坑倒塌事故中[2]，整个支护结构平面存在一处弯段，外凸的地下连续墙产生反向拱效应，导致钢支撑脱落，最后整体失稳。

传统的基坑支护设计以单元设计为主，把边长方向上任一截面视为平面应变问题加以考虑，并借助弹性地基梁理论进行内力与变形的分析[3]。俞建霖等[4]通过三维模型数值模拟与按二维平面问题分析的结果进行比较，认为基坑存在一临界长宽比，当基坑长宽比超过临界长宽比后，土压力和支护结构水平位移才接近于按二维平面应变问题分析的结果。大量工程实践也证明简化为二维平面应变的方法仅适用于基坑较长时的坑壁中间区域[5]。另外，平面应变难以分析坑角等复杂受力区的变形及受力特性。

目前，已有学者对空间效应的影响做了分析并对传统的基坑变形理论和设计方法提出改进。Ou等[6]提出空间效应的影响范围与基坑的长宽比密切相关。刘念武等[7]对内支撑结构基坑的空间效应及影响因素做了分析。李佳宇等[8]采用数值分析方法研究了坑角效应对基坑周围建筑物沉降变形的影响。周陈发等[9-10]通过对复合土钉墙进行三维有限元分析，研究了阴角和阳角处的变形和受力特性。申明亮等[11]对坑中坑的应力场进行了参数化分析。王洪新[12-15]考虑基坑平面尺寸及形状的影响，对目前规范中基坑抗隆起稳定计算和围护结构抗倾覆稳定计算方法提出修正，为狭窄基坑缩小围护结构入土深度提供了一系列理论支撑。耿大新等[16]推导了弧形地连墙侧位移计算的新方法。

本文以山东省会文化艺术中心(大剧院)基坑工程为例，利用PLAXIS 3D有限元软件建立三维整体计算模型，针对济南地区特有典型土层，揭示基坑角部、开挖宽度及坑中坑等因素的影响规律，并与基坑设计软件计算结果进行对比，明确基坑整体设计的条件和必要性。

1　工程实例

1.1　工程概况

山东省会文化艺术中心项目位于济西东路以南、腊山河西路以东。场地地下水静止水位埋深2.60～4.60 m，水位降深约6 m。大剧院区域基坑平面外圈为椭圆，内圈为不规则T形台仓，平面尺寸为64 m×42 m。台仓基坑有3个开挖深度，分别为12.75，10.4，7.45 m。考虑台仓周边标高和平面状况，将台仓侧壁划分为3个支护单元，如图1所示。支护形式采用双排桩加预应力锚杆支护结构进行支护，桩径为600 mm，桩间距为1.6 m，支护桩采用纵横冠梁连接，挂网喷混凝土。整个基坑支护范围约为270 m×230 m。

图1　台仓支护平面图Fig.1　Plane Map of Platform Silo

台仓周边布满水泥粉煤灰碎石桩(CFG)群桩，桩径为400 mm，有效桩长为14 m，桩身混凝土强度等级为C20，桩间距分为1.2，1.6，2.4 m三种。坑底布设混凝土灌注桩，桩身强度等级为C35，桩径为600 mm。

1.2　三维模型计算分析

采用有限元软件PLAXIS对开挖过程进行数值模拟。为减小计算模型规模，参考基坑中轴线位置，建立对称的1/2模型，其中，模型长边方向为X方向，短边方向为Y方向，如图2所示。

图2　有限元模型Fig.2　Finite Element Model

基坑分层开挖，并假设地下水已在基坑开挖前降到基坑底-18 m位置处，不考虑流固耦合，仅考虑地下水侧压力作用。共生成486 977个单元和820 896个节点。模型的边界条件采用PLAXIS 3D中默认的边界约束，即侧面采用水平方向的约束，底部采用固定约束，上表面自由。

预应力锚索自由段采用点对点锚杆单元模拟，嵌固段采用Embedded Pile单元模拟，锚索相关参数取值见表2。

双排桩采用梁单元模拟，CFG桩和桩基灌注桩均采用Embedded Beam单元模拟。单排桩等刚度代换为板单元，支护结构排桩墙按线弹性考虑，采用板单元模拟，由公式(1)进行等刚度代换[18]

表1　各土层力学参数Tab.1　Mechanical Parameter of Each Soil Layer

表2　锚索参数Tab.2　Parameters of Anchor

(1)

式中：D为桩径；t为两桩间隔距离；h为等效板的厚度。

放坡边坡挂网喷混凝土也采用板单元模拟，排桩和挂网的钢筋没有单独考虑，而将其刚度拟合到混凝土中，适当提高混凝土的标号等级刚度，模型中各支护桩参数见表3。

表3　支护桩参数Tab.3　Parameters of Support Pile

PLAXIS 3D有限元软件中，采用界面单元来模拟土与桩的接触，界面单元的属性与周围土体参数有关，在土体硬化模型条件下，强度折减系数Rinter为主要界面参数。真实土-结构相互作用中界面要比周围土体弱，柔性也较大，根据建议取值，本文模型取Rinter=0.7，施工步骤见表4，支护结构如图3所示。

表4　基坑施工步骤Tab.4　Construction Steps of Foundation Pit

图3　支护结构Fig.3　Supporting Structure

2　计算结果分析

为揭示整体模型空间受力变形的客观规律，并清晰准确地加以描述，选取模型几个重点位置进行分析，各双排桩在基坑中的位置见图4。

图4　剖面位置示意图Fig.4　Section Location Diagram

2.1　空间效应影响分析

图5　支护结构侧向变形Fig.5　Deformation of Supporting Structure

图5为基坑开挖结束后支护结构侧向变形。由图5可知，坑角部位支护结构侧向变形最小，随着与坑角部位距离的增加，其变形逐渐增大，至中间位置处达到最大值，并且基坑阳角处的位移要明显大于阴角处。阴角部位对基坑的位移抑制作用明显，而阳角部位则需重点关注。

2.1.1基坑阴角效应

(1)阴角区变形分析

阴角效应产生的原因在于基坑角边界的限制作用，根据圣维南原理，这种限制必然有一定的影响范围，且这种限制随着与基坑角边界距离的增大而逐渐减小。

图6　Ⅰ区和Ⅱ区支护桩桩顶水平位移曲线Fig.6　Horizontal Displacement Curves of Support Piles in Districts Ⅰ，Ⅱ

图6为不同步骤下Ⅰ区和Ⅱ区支护桩桩顶水平位移随Y轴坐标的分布曲线。从图6可以看出，两区支护结构的水平位移变化趋势很相似。随着基坑开挖深度的增加，支护桩顶部位移均不断增大。由于阴角效应的影响，支护桩的水平位移曲线呈现坑壁中央区域大、坑角处小的特点。中央区域与坑角处位移相比较，开挖结束时坑壁中央处位移增加约1倍。

因此，在支护结构最大水平位移满足设计要求的情况下，可适当减弱阴角附近区域的支护结构强度。对于本工程而言，坑壁中央区域最大水平位移约为坑角的2倍，故可将坑角区域支护结构强度减小1/2。

(2)阴角效应分析

为明确阴角效应的影响范围，取长为100 m的矩形基坑进行研究。由于结构对称，取四分之一结构建立模型。在不同开挖深度H下基坑长边的位移沿基坑坑壁的变化曲线如图7所示。

图7　长边桩顶水平位移曲线Fig.7　Horizontal Displacement Curves of Pile Top in Long Side

由图7可以看出，桩顶水平位移沿坑角向中部逐渐增大，并在距坑角一定距离处趋于稳定。以挖深-17 m为例，在0～34 m范围位移增加比较明显，超过34 m以后位移基本达到稳定。可以看出，随着开挖深度的增大，阴角效应的影响范围也逐渐增大。当基坑开挖深度分别为-5，-9，-13，-17，-21，-25 m时，空间效应影响范围依次为10，21，28，34，42，50 m。虽然阴角效应的影响范围随开挖深度的增大不断增加，但是其影响范围约为2倍挖深。

2.1.2基坑阳角效应

(1)阳角区变形分析

Ⅲ区为阳角区，不同步骤下Ⅲ区桩顶水平位移随X轴坐标的分布情况见图8。相同开挖宽度条件下，阳角处的位移大于阴角处。随着开挖的进行，基坑的阳角效应愈发明显，开挖结束后，阳角处水平位移接近最大值，约为阴角处位移的8倍。相比于Ⅰ区和Ⅱ区，Ⅲ区阴角效应对水平位移的控制能力减弱，且影响范围缩小，约为0.9倍挖深。基坑阳角非常不利于基坑围护结构的稳定。

图8　Ⅲ区支护桩桩顶水平位移曲线Fig.8　Horizontal Displacement Curves of Pile Top of Support Pile in District Ⅲ

究其原因是由于阳角有两侧土体出现临空面，造成坑外土体向阳角处汇聚(图9)，应力状态异于规则深基坑开挖面，对土体应力水平等因素更为敏感，在一定范围内减弱了基坑阴角效应的影响。

图9　土体水平位移矢量图Fig.9　Horizontal Displacement Vector Graph of Soil

(2)阳角效应分析

大众传媒所重构出的“鲁迅形象”有其局限性，这让我们反思“百家讲坛式”传播方式是不是经典普及大众的最优一种。在“自媒体”的时代，知识分子、大众媒体应该承担怎样的责任、采用何种有效的方式？我无力回答这样宏大的话题，但非常明确的是艺术发展的主流是趋向大众。无论是像法国学者和艺术家那样投入到旨在沟通与公众联系的知识和社会运动中，还是要求大众媒体在一个自由度有限的空间中自觉抵制坏趣味的形成，这都是需要长期探索的。

为了进一步探究基坑阳角效应的影响因素，图10给出了不同长深比L/H(L为坑壁长度)下支护结构随施工开挖的水平位移。由图10可知，随着L/H的减小，支护结构在阴角处位移变化很小，阳角处位移显著增大，基坑的阳角效应呈增大趋势，支护结构的水平位移曲线由最开始的抛物线形逐渐变为镰刀形。当L/H减小到1时，阳角效应的影响接近极限，此后不再变化。另外，基坑最大水平位移并非出现在阳角转折处(∠C)，而是出现在临近阳角的区域，该处为阳角最危险区域，原因是在阳角转折处阳角两面互相支撑，对其位移有一定的约束作用。

图10　阳角处与阴角处水平位移对比Fig.10　Comparisons of Horizontal Displacements Between Positive and Negative Corners

2.1.3基坑开挖宽度影响分析

桩6和桩9支护桩相同，同为阳角桩，挖深均为-12.75 m，但距墙开挖宽度不同，其中桩9开挖宽度为38.2 m，桩6开挖宽度为16.2 m。

桩6与桩9水平位移对比见图11，两者水平位移变化趋势均为复合型变形模式，前桩的位移大于后桩的位移，桩9前、后桩位移均分别大于桩6前、后桩位移，其中前排桩位移增幅为14.8%。基坑开挖宽度的影响不容忽视。

图11　桩6与桩9水平位移对比Fig.11　Comparisons of Horizontal Displacements Between Pile 6 and Pile 9

桩6前桩与桩9前桩的弯矩对比见图12，两者弯矩变化趋势基本一致，其后桩的变化趋势也基本一致，桩9前、后桩的弯矩值均略大于桩6。

图12　桩6与桩9弯矩对比Fig.12　Comparisons of Bending Moments Between Pile 6 and Pile 9

支护桩长度取为40 m，改变基坑开挖宽度B，各开挖工况下支护结构最大水平位移随宽度的变化曲线见图13。图13中实线表示不同挖深下按二维平面问题分析(基坑宽度相同)时围护结构的最大水平位移。从图13可以看出，各施工工况下支护结构最大水平位移随B值的增加而增加。前期增加趋势较为明显，后期逐渐平缓，最终趋于收敛，接近二维计算结果。开挖深度越大，收敛越慢。数值计算结果显示当基坑开挖深度超过-15 m时宽度影响已不能忽视。

图13　支护结构最大水平位移随开挖宽度变化曲线Fig.13　Variation Curves of Maximum Side Shift of Supporting Structure with Excavation Width

将图13计算结果进行数学拟合，总结出可以考虑基坑开挖深度、插入深度以及宽度对基坑变形影响的基坑变形计算公式，判定系数R2达到0.99。围护结构最大水平位移为

(2)

式中：y为支护结构水平位移；y1为平面计算所得支护结构水平位移；D′为支护结构插入深度。

2.1.4坑中坑影响分析

图14　歌剧院剖面图(单位:mm)Fig.14　Profile of Opera House (Unit:mm)

图14为歌剧院剖面图[19]。由于歌剧院内部空间功能多样，各舞台及台仓标高各异，基坑需要进行多次开挖，涉及到坑中坑的问题。坑中坑的存在使得基坑设计越来越复杂化。对于计算深度的选取，若忽略坑中坑的影响，则设计偏于不安全；若将计算深度取为基坑的最大深度，则会造成经济上的浪费。因此，有必要对坑中坑的影响范围进行研究。

台仓基坑CD边(图2)一侧开挖深度为-7.6 m，外坑开挖深度为-9 m，挡墙AB为悬臂式支护结构，距台仓基坑边缘CD的距离约为50 m。现取挡墙AB在台仓开挖前后沿深度方向的变形进行研究。

图15为台仓开挖前后挡墙水平位移对比。台仓开挖前后挡墙AB的水平位移分别为13.9 mm和14.2 mm，变化很小，表明内坑的开挖对挡墙产生的影响可忽略。有研究表明[20]，内外坑地墙间距超过某一临界值时，外坑受到的变形影响可以忽略。

图15　内坑开挖前后支护结构水平位移对比Fig.15　Comparison of Horizontal Displacement of Supporting Structure Before and After Excavation of Inner Pit

现定义坑趾系数χ=d/H′，其中d为内坑边缘到外坑边缘的距离，H′为外坑挖深，深度比α=h′/H′，其中h′为内坑开挖深度。图16为不同基坑深度比下外坑支护结构最大水平位移随坑趾系数的变化曲线。由图16可知，随着坑趾系数的增大，外坑支护结构水平位移逐渐减小，前期变化较快，后期逐渐变缓。深度比越大，外坑支护结构水平位移也越大。这说明坑中坑外坑支护结构的侧向变形不仅与深度比有关，还与坑趾系数有关。另外，当χ大于2.5时，外坑支护结构基本不受内坑的影响。

图16　支护结构最大水平位移随坑趾系数的变化Fig.16　Changes of Maximum Side Shift of Supporting Structure with Pit Toe Coefficient

2.2　不同计算方法结果对比

选取图4中支护桩2作为分析对象。支护桩2位于Ⅲ区开挖边中点位置。支护单元剖面见图17。用理正6.0基坑软件建立二维平面计算模型，对支护桩2进行了计算，并与PLAXIS 3D建立的单元计算模型和整体计算模型结果进行对比。

图17　计算单元剖面(单位:mm)Fig.17　Profile of Calculation Element (Unit:mm)

图18～20为对支护桩2采用3种计算方法的结果对比曲线。3种计算方法得到的支护桩水平位移、弯矩以及剪力变化趋势一致，但二维计算结果最大，单元计算结果次之，整体计算结果最小。这是由于支护桩顶部设有纵横冠梁，二维计算模型忽视了坑角效应及横向冠梁的影响，而单元计算模型只忽视坑角效应的影响，故产生上述结果。

图18　水平位移对比Fig.18　Comparisons of Horizontal Displacements

图19　弯矩对比Fig.19　Comparisons of Bending Moments

图20　剪力对比Fig.20　Comparisons of Shear Forces

表5为不同计算方法得到的变形和内力结果最大值的比较。通过对比发现，单元计算和二维计算得到的支护桩最大侧向变形较整体计算结果分别增加22.1%和19.2%，弯矩分别增加4.1%和18%，剪力分别增加17.8%和32.5%。整体计算模型中考虑了基坑的空间效应，且实际工程中支护桩2虽然位于基坑边中点位置，但由于基坑平面形状复杂，使得该段开挖边长较短，支护桩距基坑阴角大约只有1倍开挖深度，处于空间效应的影响范围中，故支护桩的最大侧向变形及内力均小于单元计算和二维计算结果。可见，基坑的单元计算和二维计算所得结果偏于保守，在平面形状复杂的重大基坑中，空间效应的影响较大，不容忽视。

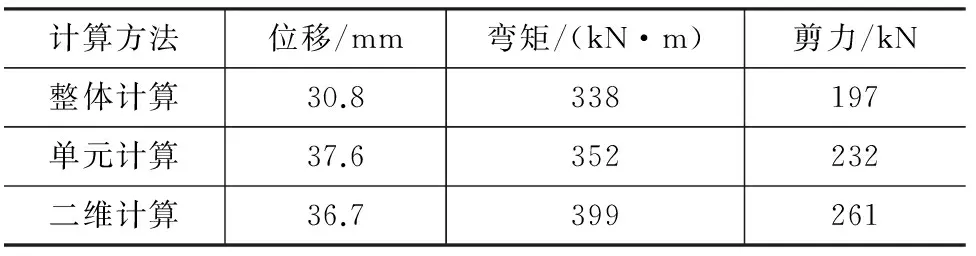
表5　支护结构变形及内力最大值比较Tab.5　Maximum Value Comparisons of Deformation and Internal Force of Supporting Structure

3　结语

(1)支护结构越靠近基坑阴角，其变形越小，故在设计、施工时基坑两端部位可适当减弱支护强度，节省工程造价。济南地层条件下，基坑阴角效应影响范围约为2倍开挖深度。

(2)基坑阳角和阴角距离较近，会使二者的作用在一定程度上相互抵消。阳角效应随基坑长深比的减小不断增大，当长深比小于1时，达到极限。

(3)随着基坑开挖宽度的增加，支护结构的水平位移呈先增大后保持稳定的趋势。基坑开挖深度越大，基坑开挖宽度的影响也增大。数值计算结果显示当基坑开挖深度超过-15 m时，宽度的影响已不能忽视。

(4)对于坑中坑的影响，支护结构水平位移随内外坑深度比的增度大而增大，随坑趾系数的增大而减小，当坑趾系数超过2.5时，支护结构基本不受内坑开挖的影响。

(5)相比于基坑整体计算结果，单元计算和二维平面计算结果偏于保守。考虑土体-支护结构共同作用的三维有限元整体计算模型能够考虑基坑角部、开挖宽度及坑中坑等多种因素的影响，可用于基坑精细设计。

参考文献：

[1]郑刚,朱合华,刘新荣,等.基坑工程与地下工程安全及环境影响控制[J].土木工程学报,2016,49(6):1-24.

ZHENG Gang,ZHU He-hua,LIU Xin-rong,et al.Control of Safety of Deep Excavations and Underground Engineering and Its Impact on Surrounding Environment[J].China Civil Engineering Journal,2016,49(6):1-24.

[2]程雪松,郑刚,邓楚涵,等.基坑悬臂排桩支护局部失效引发连续破坏机理研究[J].岩土工程学报,2015,37(7):1249-1263.

CHENG Xue-song,ZHENG Gang,DENG Chu-han,et al.Mechanism of Progressive Collapse Induced by Partial Failure of Cantilever Contiguous Retaining Piles[J].Chinese Journal of Geotechnical Engineering,2015,37(7):1249-1263.

[3]郑刚,李志伟.坑角效应对基坑周边建筑物影响的有限元分析[J].天津大学学报,2012,45(8):688-699.

ZHENG Gang,LI Zhi-wei.Finite Element Analysis of Adjacent Building Response to Corner Effect of Excavation[J].Journal of Tianjin University,2012,45(8):688-699.

[4]俞建霖,龚晓南.深基坑工程的空间性状分析[J].岩土工程学报,1999,21(1):21-25.

YU Jian-lin,GONG Xiao-nan.Spatial Behavior Analysis of Deep Excavation[J].Chinese Journal of Geotechnical Engineering,1999,21(1):21-25.

[5]徐中华.上海地区支护结构与主体地下结构相结合的深基坑变形性状研究[D].上海:上海交通大学,2007.

XU Zhong-hua.Deformation Behavior of Deep Excavations Supported by Permanent Structure in Shanghai Soft Deposit[D].Shanghai:Shanghai Jiaotong University,2007.

[6]OU C Y,SHIAU B Y,WANG I W.Three-dimensional Deformation Behavior of the Taipei National Enterprise Center (TNEC) Excavation Case History[J].Canadian Geotechnical Journal,2000,37(2):438-448.

[7]刘念武,龚晓南,俞峰,等.内支撑结构基坑的空间效应及影响因素分析[J].岩土力学,2014,35(8):2293-2298,2306.

LIU Nian-wu,GONG Xiao-nan,YU Feng,et al.Analysis of Spatial Effects in Strutted Excavation and Related Influential Factors[J].Rock and Soil Mechanics,2014,35(8):2293-2298,2306.

[8]李佳宇,陈晨.坑角效应对基坑周围建筑物沉降变形影响的研究[J].岩土工程学报,2013,35(12):2238-2246.

LI Jia-yu,CHEN Chen.Response of Settlement and Displacement of Adjacent Buildings of Excavations to Corner Effect[J].Chinese Journal of Geotechnical Engineering,2013,35(12):2238-2246.

[9]周陈发,潘泓.复合土钉墙阳角部区域土钉受力性状分析[J].地下空间与工程学报,2007,3(7):1310-1313.

ZHOU Chen-fa,PAN Hong.Analysis on Pull of Soil Nail at Convex Location of Composite Soil Nailing Wall[J].Chinese Journal of Underground Space and Engineering,2007,3(7):1310-1313.

[10]潘泓,周陈发,曹洪.复合土钉墙的角部空间效应及变形性状分析[J].岩土力学,2008,29(2):333-336.

PAN Hong,ZHOU Chen-fa,CAO Hong.Analysis of Spatial Effect and Deformation of Corner of Composite Soil Nailing Walls[J].Rock and Soil Mechanics,2008,29(2):333-336.

[11]申明亮,廖少明,周小华,等.坑中坑基坑应力场的参数化分析[J].岩土工程学报,2010,32(增2):187-191.

SHEN Ming-liang,LIAO Shao-ming,ZHOU Xiao-hua,et al.Parametric Analysis on Stress Field of Pit in Pit Excavation[J].Chinese Journal of Geotechnical Engineering,2010,32(S2):187-191.

[12]王洪新.对基坑抗隆起稳定安全系数的改进[J].岩土力学,2014,35(增2):30-36.

WANG Hong-xin.Improvement on Safety Coefficient of Heave-resistant Stability of Excavations[J].Rock and Soil Mechanics,2014,35(S2):30-36.

[13]王洪新.基坑宽度对围护结构稳定性的影响[J].土木工程学报,2011,44(6):120-126.

WANG Hong-xin.Influence of Excavation Width on Enclosure-structure Stability of Foundation Pits[J].China Civil Engineering Journal,2011,44(6):120-126.

[14]王洪新.考虑二维和三维尺寸效应的基坑抗隆起稳定安全系数[J].岩土工程学报,2013,35(11):2144-2152.

WANG Hong-xin.Safety Factor of Heave-resistant Stability Considering Two- and Three-dimensional Size Effects of Foundation Pits[J].Chinese Journal of Geotechnical Engineering,2013,35(11):2144-2152.

[15]王洪新.考虑基坑形状和平面尺寸的抗隆起稳定安全系数及异形基坑的稳定性分析[J].岩石力学与工程学报,2015,34(12):2559-2571.

WANG Hong-xin. A Coefficient of Heave-resistant Stability Considering Shapes and Plane Sizes and Its Application to the Stability Analysis of Shaped Excavations[J].Chinese Journal of Rock Mechanics and Engineering,2015,34(12):2559-2571.

[16]耿大新,余小强,童立红,等.弧形地连墙侧位移计算的新方法[J].岩土工程学报,2016,38(12):2272-2277.

GENG Da-xin,YU Xiao-qiang,TONG Li-hong,et al.New Method for Calculating Lateral Displacement of Curved Ground Wall[J].Chinese Journal of Geotechnical Engineering,2016,38(12):2272-2277.

[17]徐中华,王卫东.敏感环境下基坑数值分析中土体本构模型的选择[J].岩土力学,2010,31(1):258-264,326.

XU Zhong-hua,WANG Wei-dong.Selection of Soil Constitutive Models for Numerical Analysis of Deep Excavations in Close Proximity to Sensitive Properties[J].Rock and Soil Mechanics,2010,31(1):258-264,326.

[18]刘国彬,王卫东.基坑工程手册[M].2版.北京:中国建筑工业出版社,2009.

LIU Guo-bin,WANG Wei-dong.Excavation Engineering Manual[M].2nd ed.Beijing:China Architecture & Building Press,2009.

[19]韩巍,齐欣,张学利,等.济南省会文化艺术中心(大剧院)结构设计[J].建筑结构,2013,43(17):48-53,8.

HAN Wei,QI Xin,ZHANG Xue-li,et al.Structural Design on the Building of Jinan Provincial Capital Culture and Art Center[J].Building Structure,2013,43(17):48-53,8.

[20]霍军帅,宫全美,陈娟.坑中坑基坑围护结构变形特性分析[J].土木建筑与环境工程,2011,33(增1):139-142,208.

HUO Jun-shuai,GONG Quan-mei,CHEN Juan.Analysis of the Deformation of Retaining Structure of Pit-in-pit Excavation[J].Journal of Civil,Architectural & Environmental Engineering,2011,33(S1):139-142,208.