不同分布筋间距下型钢混凝土剪力墙抗震性能试验

王玉镯，高　英，王慧敏，傅传国

(1. 山东建筑大学土木工程学院，山东济南　250101； 2. 山东协和学院建筑工程学院，山东济南　250107；3. 山东职业学院铁道工程与土木工程系，山东济南　250104)

0　引　言

地震是严重危害人类生命安全和社会发展的自然灾害之一。虽然人类对地震和抗震等方面进行了大量的研究，取得了令人瞩目的成果，但新型抗震结构体系仍然是当今工程结构领域关注的热点。型钢混凝土剪力墙因具有强度高、刚度大、稳定性好等优点，被广泛地应用于高层建筑结构中[1-2]。目前型钢混凝土剪力墙抗震性能方面的研究也越来越多[3-8]，孙建超等[9]对13片混凝土剪力墙试件(高宽比为1.5，轴压比为0.5)进行了抗震性能试验研究，通过考虑配筋方式、分布筋配筋率(0.35%～1.96%)等因素，得到墙体分布筋配筋率的增加可提高剪力墙的受剪承载力，但配筋率过高，其延性反而很差。梁兴文等[10]对不同剪跨比型钢高性能混凝土剪力墙(其端部约束边缘构件的含钢率分别为8.4%和6.9%)进行了低周反复荷载下的试验研究，结果表明：型钢高性能混凝土剪力墙的破坏形态与水平分布钢筋的相对数量有关，水平分布钢筋相对数量越多，试件延性越好。方小丹等[11]对7个不同形式的高配筋率边缘约束构件高强混凝土剪力墙试件(边缘约束构件内的纵筋配筋率为5%～8%)和1个普通配筋率(配筋率为1.58%)的高强混凝土剪力墙试件进行了低周反复荷载试验，结果表明：在一定条件下，适当提高分布钢筋配筋率，可以显著提高高强混凝土剪力墙的抗震性能。

综上所述，现有研究主要考虑了配筋方式、配筋率等因素对型钢混凝土剪力墙试件抗震性能的影响。为了研究分布筋间距对型钢混凝土剪力墙抗震性能的影响，本文设计了4个具有不同分布筋间距的型钢混凝土剪力墙试件，进行了低周反复加载下的试验研究。

1　试验概况

1.1　试件设计

本文试验共设计了4个矩形截面(800 mm×200 mm)剪力墙试件，其剪跨比均为1.75，试件编号分别为JLQ-1，JLQ-2，JLQ-3和JLQ-4，其中JLQ-1为普通无暗撑对比试件，JLQ-2，JLQ-3，JLQ-4为带X形暗撑且具有不同分布筋间距的试件。试件采用C50商品混凝土，分布筋及主筋全部采用HPB300钢筋，拉筋用φ6.5的钢筋梅花型布置。试件配筋及具体参数情况如图1和表1所示。

1.2　材性试验

试件的制作是在工地中进行的，按照放置型钢、绑扎钢筋、支护模板、浇筑、养护、拆模的顺序进行。浇筑混凝土时制作了1组(共3块)混凝土立方体标准试块[12]，自然养护28 d，取其强度平均值，结果如表2所示。对钢筋及型钢进行力学性能测试，结果如表3，4所示。

1.3　试验装置及加载制度

1.3.1试验装置

伺服液压加载系统(MTS)可较精确地模拟实际荷载，常用来进行试件抗震性能试验研究。本文利用伺服液压加载装置进行了低周反复加载试验[13-15]。试验装置主要由竖向加载装置(由竖向液压千斤顶和分配梁组成)和水平加载装置(主要由水平作动器和水平连接装置组成)两部分组成，如图2所示。

1.3.2加载制度

为了模拟构件在结构中的实际受力条件及构件在遭受地震时的情况，试验采用如下加载制度。

竖向加载：试件轴压比控制为0.18。试验开始前，竖向荷载由千斤顶通过分配梁施加在试件上，分2级加载，加载至荷载F=550 kN，整个试验过程中保持不变，其作用线通过试件截面竖向中心线。

水平加载：距离基础顶面1 400 mm高度处用MTS施加反复水平荷载，首先施加F=80 kN的水平力，然后逐级(每一个循环增加10 kN)加载直至试件表面出现裂纹，进入位移控制加载。在开裂荷载所对应的试件水平位移基础上，以2 mm为级差进行位移控制加载，每级位移循环2次。当试件水平承载力降至极限承载力的85%时，加载结束。加载制度见图3。

1.4　测试内容及测点布置

图1　各试件配筋(单位:mm)Fig.1　Reinforcement of Specimens (Unit:mm)

针对不同的测量目的，在试件不同位置布置不同间距的应变片或应变花，用联机数据采集系统采集与水平力相应高度处剪力墙的水平位移、水平荷载值，用X-Y函数记录仪记录构件内部的钢筋应变以及型钢应变等。剪力墙混凝土应变(TS)、剪力墙水平钢筋应变(RHS)、剪力墙竖向钢筋应变(RVS)和暗支撑型钢应变(XS)的测点布置如图4所示。

表1　剪力墙试件参数Tab.1　Parameters of Shear Wall Specimens

表2　混凝土的力学性能指标Tab.2　Mechanical Performance Indexes of Concrete

表3　钢筋的力学性能指标Tab.3　Mechanical Performance Indexes of Steel Bars

表4　型钢的力学性能指标Tab.4　Mechanical Performance Indexes of Steel

图2　试验加载装置Fig.2　Test Loading Device

图3　位移控制加载曲线Fig.3　Loading Curve Under Displacement Control

图4　应变测点布置(单位:mm)Fig.4　Arrangement of Strain Measuring Points (Unit:mm)

2　试验现象分析

本文试验是在山东建筑大学工程结构与防灾减灾实验室中进行。试件的位移-力关系由MTS在试验过程中自动记录。

2.1　试件JLQ-1

当位移Δ=2 mm时，距离A端底部33 cm处出现第1条裂缝并呈水平状发展趋势；当位移Δ=-6 mm时，在距离B端底部33 cm处出现第2条裂缝；当位移Δ=8 mm时，墙体底部开始出现水平裂缝；当位移Δ=14 mm时，墙体A端底部受压区混凝土压坏并开始剥落；当位移Δ=-26 mm时，墙体中部混凝土开始剥落；当位移Δ=28 mm时，水平承载力下降至极限承载力的85%，试验终止。试件破坏形态如图5(a)所示。

2.2　试件JLQ-2

当位移Δ=4 mm时，距A端底部48 cm处出现第1条裂缝；当位移Δ=-6 mm时，距B端底部48 cm处出现第2条裂缝，且裂缝末端有小裂缝出现；当位移Δ=22 mm时，距B端根部混凝土压碎并有少许剥落；当位移Δ=36 mm时，B端混凝土破坏严重；当位移Δ=-36 mm时，A端混凝土出现较严重的剥落现象；当位移Δ=46 mm时，A，B两端均破坏严重，水平承载力下降至极限承载力的85%，试验终止。试件破坏形态如图5(b)所示。

2.3　试件JLQ-3

当位移Δ=4 mm时，距A端根部41 cm处出现第1条裂缝；当位移Δ=-6 mm时，距B端根部37 cm处出现第2条裂缝；当位移Δ=10 mm时，距A端底部21 cm处出现新的裂缝；当位移Δ=22 mm时，A端原有裂缝继续发展且B端部分混凝土出现剥落现象；当位移Δ=34 mm时，A端裂缝迅速发展，发展成主裂缝；当位移Δ=36 mm时，水平承载力下降至极限承载力的85%，试验终止。试件破坏形态如图5(c)所示。

图5　各试件破坏形态Fig.5　Failure Modes of Specimens

2.4　试件JLQ-4

当位移Δ=4 mm时，距A端底部18 mm处出现第1条裂缝并呈水平状发展趋势；当位移Δ=-6 mm时，距B端底部40 cm处出现第2条裂缝并呈水平状发展趋势；当位移Δ=-20 mm时，B端根部裂缝迅速发展并与A端裂缝相贯通；当位移Δ=-22 mm时，B端混凝土剥落严重，钢筋裸露；当位移Δ=28 mm时，B端混凝土剥落严重；当位移Δ=34 mm时，两端混凝土均被压碎，水平承载力下降至极限承载力的85%，试验终止。试件破坏形态如图5(c)所示。

2.5　破坏形态分析

通过对比分析上述4个试件的破坏形态，可得如下结论：

(1)对比试件JLQ-1的主裂缝呈现剪切破坏，试件JLQ-2，JLQ-3，JLQ-4的主裂缝呈现弯曲破坏。

(2)相对于对比试件JLQ-1，试件JLQ-2的裂缝宽度变小，裂缝数量明显增多，塑性铰范围扩大，耗能能力明显提高，说明型钢暗撑有利于提高试件的耗能能力。

(3)试件JLQ-2，JLQ-3，JLQ-4中，试件JLQ-3裂缝最多，分布最广，且沿暗撑走向分布明显，塑性铰范围最大，这表明JLQ-3的耗能能力最好。同时从各试件破坏形态中发现，试件JLQ-3受压区混凝土被压碎剥落的程度最轻，说明试件JLQ-3的抗震性能最好。

2.6　应变分析

钢筋和型钢的应变可以进一步说明试件的受力机理，本文选取型钢应变测点XS2、水平钢筋应变测点RHS1和竖向钢筋应变测点RVS1的应变值进行分析，结果如图6所示。图6中设定型钢和钢筋应变值，当应变测点处型钢或钢筋受拉时应变值为正，受压时应变值为负。

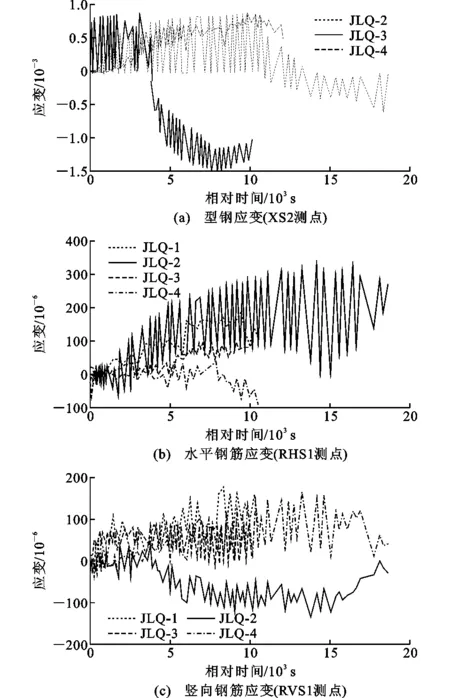
图6　试件应变分析结果Fig.6　Strain Analysis Results of Specimens

由图6可知：整体上试件内的型钢应变水平要大于钢筋应变水平；试件JLQ-3的型钢应变水平最大，波动性也大，试件JLQ-2的应变水平其次，试件JLQ-4的应变水平最小，这表明试件内分布筋越密，内部型钢应变越大；总体上，试件的竖向钢筋应变水平较水平钢筋应变水平小，且无论竖向钢筋应变还是水平钢筋应变，试件JLQ-3的应变水平最低，即试件JLQ-3的抗变形能力最好。

3　试验结果分析

3.1　滞回曲线

滞回曲线是试件水平反复荷载与水平位移的直接体现，其数据由MTS直接采集并记录。各试件滞回曲线如图7所示。

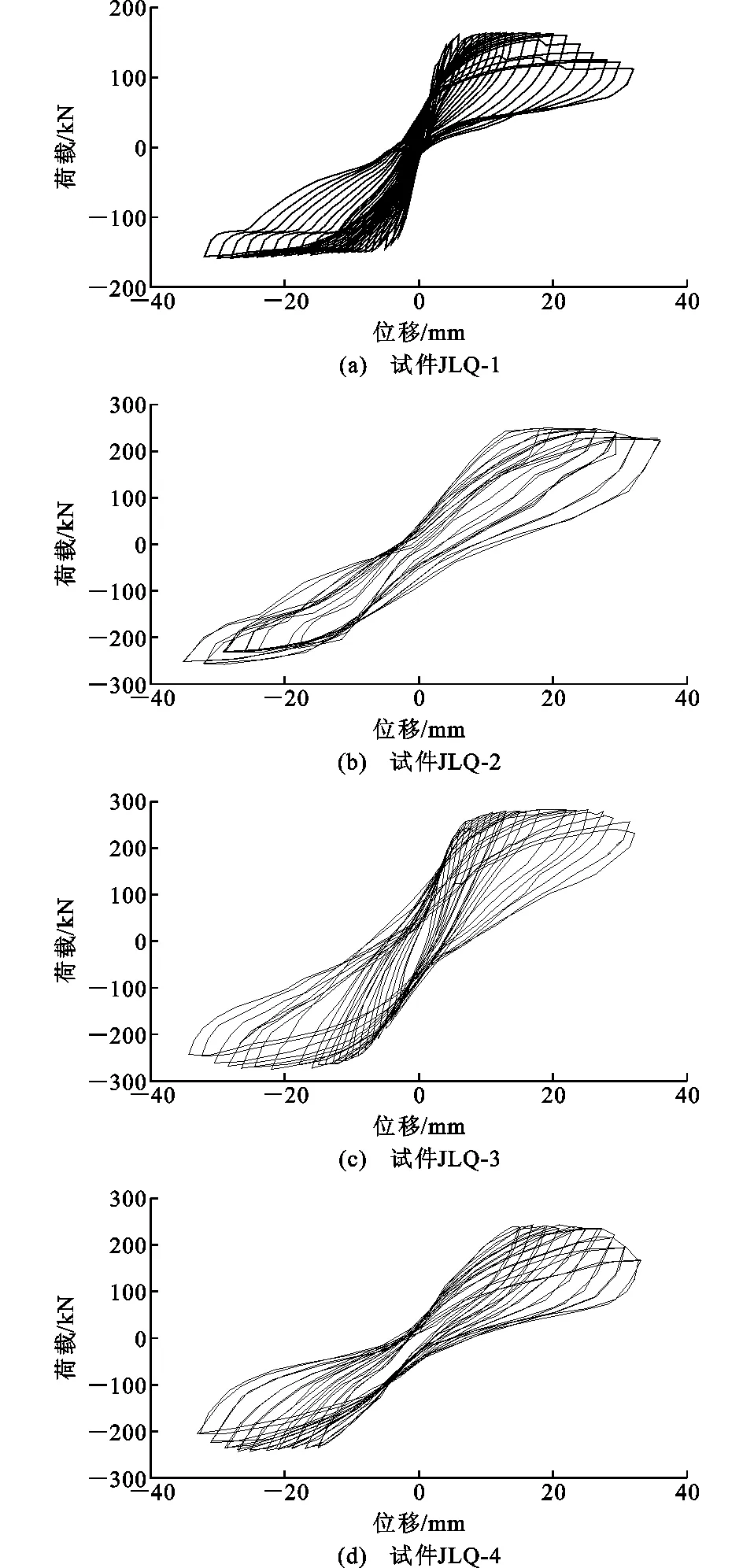
图7　各试件滞回曲线Fig.7　Hysteretic Curves of Specimens

由图7可知：

(1)随着位移的增大，试件滞回环逐渐变饱满，所围面积增大，滞回曲线开始向位移轴倾斜，刚度退化逐渐明显，残余变形不断积累直至加载结束。

(2)相对于对比试件JLQ-1，试件JLQ-2的滞回环相对饱满，所围面积变更大，说明其耗能能力明显提高。

(3)试件JLQ-4的滞回曲线有明显的捏缩现象，黏结滑移相对严重；试件JLQ-2的滞回曲线捏缩现象最不明显，黏结滑移相对较轻。说明分布筋间距对试件内部的黏结滑移有影响，分布筋间距越大，黏结滑移相对越大。

(4)相对于对比试件JLQ-1，试件JLQ-2，JLQ-3及JLQ-4的滞回环面积明显增大，表明型钢暗撑提高了试件的耗能能力。

3.2　骨架曲线

骨架曲线是每次循环加载达到水平承载力最大值的轨迹，反映了构件受力与变形的不同阶段及特性(强度、刚度、延性、耗能及抗倒塌能力等)。各试件正负向骨架曲线趋势相同，整体发展形势基本一致(图8)。

图8　各试件骨架曲线Fig.8　Skeleton Curves of Specimens

由图8可知：

(1)各试件初始刚度基本一致，说明暗撑及分布筋间距对试件的初始刚度无显著影响，试件初始刚度只与试件的截面尺寸以及混凝土的强度等级有关。

(2)试件JLQ-3的承载能力最大；试件JLQ-2的承载能力次之；试件JLQ-4的承载能力最小。

(3)试件JLQ-3的屈服段最长，试件JLQ-2的屈服段次之，试件JLQ-4的屈服段最短，表明分布筋对试件的耗能有显著影响，且分布筋间距越小，试件的耗能越大，分布筋间距越大，试件的耗能越低，试件的耗能随分布筋间距的增大而减小。

(4)试件JLQ-2骨架曲线的下降段下降最缓慢，表明试件JLQ-2在加载后期有较好的塑性变形能力。

3.3　承载力分析

各试件的开裂荷载、屈服荷载和极限荷载及其比值如表5所示，同时将各荷载值与分布筋间距的关系整理成图10。表5中Fcr为开裂荷载，Fy为屈服荷载，Fu为极限荷载，μcu为开裂荷载与极限荷载的比值，μcu=Fcr/Fu，μyu为屈服荷载与极限荷载的比值，μyu=Fy/Fu，Fcr，Fy，Fu均取正负两向加载均值。屈服荷载采用通用弯矩屈服法[14]确定。通用弯矩屈服法如图9所示。图9中，过原点的弹性理论值OA线与过极限荷载点的水平线相交于A点，过A点作垂线与骨架曲线相交于B点，连接OB并延长，与过极限荷载点的水平线交于C点，过C点作垂线与骨架曲线相交于D点，D点即为屈服荷载点，Δy为屈服位移。

表5　试件开裂荷载、屈服荷载、极限荷载试验值Tab.5　Test Values of Cracking Load, Yield Load and Ultimate Load

图9　通用弯矩屈服法Fig.9　Universal Moment Yield Method

图10　承载力-分布筋间距关系Fig.10　Relation of Bear Capacity and Distributed Reinforcement Spacing

由表5及图10可以看出：

(1)与试件JLQ-1相比，试件JLQ-2，JLQ-3，JLQ-4的极限承载力分别提高了45.9%，66.8%和41.0%，说明型钢剪力墙试件的承载能力较对比试件有显著提高。

(2)试件JLQ-3的Fcr，Fy，Fu三个值均最大，试件JLQ-4的Fcr，Fy，Fu三个值均最小。这说明分布筋间距越小，试件的Fcr，Fy，Fu越大，分布筋间距越大，试件的Fcr，Fy，Fu越小。

3.4　刚度退化分析

本文采用同级变形下的割线刚度[14]表示试件的刚度。割线刚度的计算方法如图11所示，即采用每个位移循环中的荷载最大值与对应位移之比作为割线刚度，每个循环的割线刚度取正向加载刚度K1和负向加载刚度K2的平均值K，最终的割线刚度取所有同级加载循环割线刚度的平均值。通过上述方法计算的割线刚度退化曲线如图12所示。

图11　割线刚度计算方法Fig.11　Secant Stiffness Calculation Method

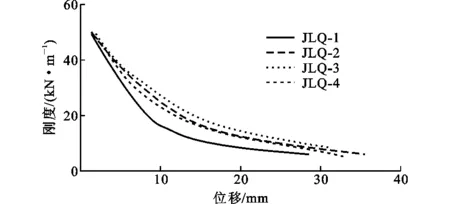
图12　试件刚度退化曲线Fig.12　Stiffness Degradation Curves of Specimens

由图12可知：

(1)加载初期，随着位移的不断增大，各试件刚度退化较快；加载后期，尤其进入屈服阶段后，各试件刚度的退化速度随位移的增大而渐趋缓慢。

(2)加载初期，各试件的刚度退化曲线基本重合，表明初始刚度基本一致。随加载的不断进行，刚度退化曲线不再一致，出现分化，具体表现在：对比试件JLQ-1的刚度退化曲线随位移的增大下降最快，处于所有曲线最下方。这说明普通剪力墙试件的刚度退化现象最严重。

(3)试件JLQ-3的后期刚度最大，试件JLQ-4的后期刚度最小。这表明分布筋间距对试件后期刚度有明显的影响，分布筋间距越小，试件的后期刚度越大。

3.5　延性分析

延性系数反映结构构件的变形能力，是评价结构抗震性能的主要指标之一。目前有关延性系数定义有很多种，本文选用以下定义：结构破坏时的极限位移Δu和屈服时的屈服位移Δy之比，即

采用基于荷载峰值的确定方法确定极限位移，采用弯矩屈服法确定屈服位移和屈服荷载，各试件的延性系数见表6。

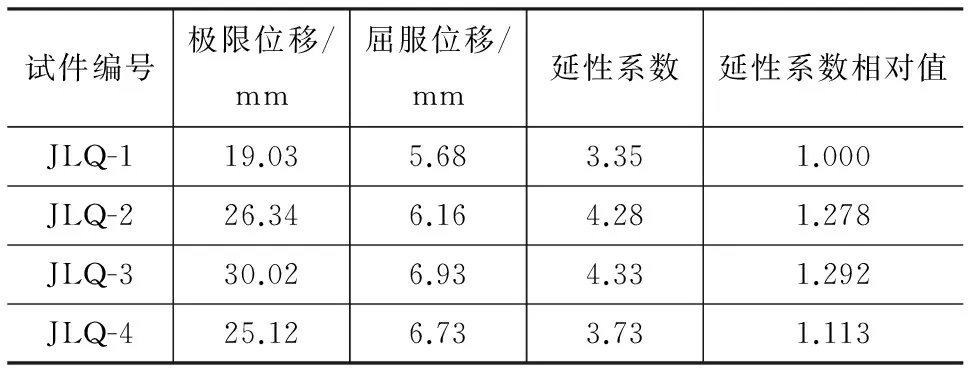
表6　试件延性系数Tab.6　Ductility Coefficients of Specimens

由表6可以得出以下结论:

(1)相对于对比试件JLQ-1，试件JLQ-2，JLQ-3，JLQ-4的延性分别提高了27.8%，29.2%，11.3%。

(2)试件JLQ-2，JLQ-3，JLQ-4中，试件JLQ-3的延性系数最大，试件JLQ-4的延性系数最小。这说明分布筋间距越小，试件延性越好，分布筋间距越大试件延性越差，且试件延性随分布筋间距的增大呈线性降低关系。

4　讨　论

考虑到普通钢筋混凝土构件存在超筋、适筋和少筋现象，即存在最佳配筋问题，因而提出假设：对于型钢混凝土构件，其分布筋也可能存在最佳间距(最佳配筋率)，即分布筋间距越小，试件的抗震性能、耗能能力、延性等未必越好。后续会通过开展大量试验来验证上述假设，并找到最佳分布筋间距。

5　结语

(1)各试件均发生弯剪破坏，其中普通剪力墙对比试件的主裂缝呈现剪切破坏，型钢混凝土剪力墙试件在剪切破坏的同时弯曲破坏更加明显，而且分布筋间距越小的试件出现的裂缝越细密，分布范围越广。

(2)当分布筋间距相同时，型钢剪力墙试件的滞回环较普通剪力墙试件饱满，耗能能力明显提高，同时延性系数较大，延性提高显著，由此可见型钢混凝土剪力墙试件在耗能和延性方面的抗震性能明显优于普通剪力墙试件。

(3)分布筋间距对试件的承载力有较大影响，分布筋间距越小，试件承载力越大；反之，分布筋间距越大，试件的承载力越小。

(4)分布筋间距对试件的初始刚度几乎无影响，但对试件的后期刚度影响较大。试件的后期刚度随着试件分布筋间距的增大而减小。试件的后期刚度均大于对比试件的后期刚度。

参考文献：

[1]HAJJAR J F.Composite Construction for Wind and Seismic Engineering[C]//Structural Stability Research Council.Proceedings of 2001 Annual Technical Session and Meeting.Bethlehem:Structural Stability Research Council,2001:209-228.

[2]董宏英,蒋峰,曹万林.钢-混凝土组合剪力墙抗震研究与发展[J].地震工程与工程振动,2012,32(1):54-61.

DONG Hong-ying,JIANG Feng,CAO Wan-lin.Development and Research in Seismic Performance of Steel-concrete Composite Shear Wall[J].Journal of Earthquake Engineering and Engineering Vibration,2012,32(1):54-61.

[3]曹万林,胡国振,周明杰,等.带暗支撑抗震墙研究[J].世界地震工程,1998,14(4):76-80.

CAO Wan-lin,HU Guo-zhen,ZHOU Ming-jie,et al.Study on Aseismic Wall with Concealed Bracings[J].World Earthquake Engineering,1998,14(4):76-80.

[4]曹万林,董宏英,胡国振,等.不同暗支撑型式的带暗支撑双肢剪力墙抗震性能试验研究[J].土木工程学报,2005，38(8):18-25.

CAO Wan-lin,DONG Hong-ying,HU Guo-zhen,et al.An Experimental Study on the Seismic Behavior of RC Coupled Shear Walls with Concealed Bracings of Different Styles[J].China Civil Engineering Journal,2005,38(8):18-25.

[5]曹万林,张建伟,常卫华,等.带暗支撑双肢短肢剪力墙抗震性能试验研究[J].世界地震工程,2006,26(1):64-70.

CAO Wan-lin,ZHANG Jian-wei,CHANG Wei-hua,et al.Experiment Study on Seismic Behavior of RC Coupled Short-pier Shear Wall with Concealed Bracings[J].World Earthquake Engineering,2006,26(1):64-70.

[6]曹万林,杨兴民,黄选明,等.带钢筋及钢骨暗支撑剪力墙抗震性能试验研究[J].世界地震工程,2005,21(1):1-6.

CAO Wan-lin,YANG Xing-min,HUANG Xuan-ming,et al.Experimental Study on Seismic Behavior of RC shear Walls with Concealed SRC Bracings[J].World Earthquake Engineering,2005,21(1):1-6.

[7]白亮.型钢高性能混凝土剪力墙抗震性能及性能设计理论研究[D].西安：西安建筑科技大学,2009.

BAI Liang.Research on Seismic Behavior and Performance-based Seismic Design Theory of Steel High Performance Concrete Structural Walls[D].Xi’an:Xi’an University of Architecture and Technology,2009.

[8]梁兴文,杨鹏辉,崔晓玲,等.带端柱高强混凝土剪力墙抗震性能试验研究[J].建筑结构学报,2010,31(1):23-32.

LIANG Xing-wen,YANG Peng-hui,CUI Xiao-ling,et al.Experimental Studies on Seismic Behavior of High Strength Concrete Shear Wall with Boundary Columns[J].Journal of Building Structures,2010,31(1):23-32.

[9]孙建超,徐培福,肖从真,等.不同配筋形式混凝土剪力墙受剪性能试验研究[J].建筑结构,2008,38(6):6-10.

SUN Jian-chao,XU Pei-fu,XIAO Cong-zhen,et al.Experimental Study on Shear Behavior of Concrete Wall with Different Types of Reinforcement[J].Building Structure,2008,38(6):6-10.

[10]梁兴文,白亮,杨红楼,等.型钢高性能混凝土剪力墙抗震性能试验研究[J].工程力学,2010,27(10):131-138.

LIANG Xing-wen,BAI Liang,YAGN Hong-lou,et al.Experimental Study on the Seismic Behavior of High Performance Steel-concrete Shear Walls[J].Engineering Mechanics,2010,27(10):131-138.

[11]方小丹,李照林,韦宏,等.高配筋率边缘约束构件高强混凝土剪力墙抗震性能试验研究[J].建筑结构学报,2011,32(12):145-153.

FANG Xiao-dan,LI Zhao-lin,WEI Hong,et al.Experimental Study on Seismic Behavior of High Performance Concrete Shear Wall with High Reinforcement Ratio Boundary Elements[J].Journal of Building Structures,2011,32(12):145-153.

[12]GB 50010—2010,混凝土结构设计规范[S].

GB 50010—2010,Code for Design of Concrete Structures[S].

[13]黄建军.不同型式暗支撑型钢高强混凝土中高剪力墙抗震性能试验研究[D].重庆:重庆大学,2012.

HUANG Jian-jun.Experimental Study on Seismic Behavior of Steel Reinforced High-strength Concrete Medium-high Wall with Different Types of Concealed Bracings[D].Chongqing:Chongqing University,2012.

[14]JGJ/T 101—2015,建筑抗震试验规程[S].

JGJ/T 101—2015,Specification for Seismic Test of Buildings[S].

[15]唐九如.钢筋混凝土框架节点抗震[M].南京:东南大学出版社,1989.

TANG Jiu-ru.Aseismic of Reinforced Concrete Frame Joints[M].Nanjing:Southeast University Press,1989.