基于曲率模态曲线变化的桥梁损伤识别
2018-04-08刘来君张筱雨刘虹延
吴 多,刘来君,张筱雨,刘虹延
(长安大学桥梁结构安全技术国家工程实验室,陕西西安 710064)
0 引 言
桥梁在投入运营期间,由于长期受荷载(静载、动载)与自然灾害的作用(地震、台风和火灾等)会持续产生各类损伤,不同损伤累积至一定程度便会危害结构的安全状态与正常运营[1-3],这也部分印证了桥梁健康状态的劣化过程。因此,基于桥梁损伤位置的检测与损伤程度的识别研究便成为了其健康监测中的重要环节[4-6]。
随着桥梁抗风、抗震方面的研究与有限元技术、测控领域的发展,桥梁的损伤识别技术也得到很大程度的发展。近年来,由于诸多桥梁事故的发生,桥梁的健康监测越来越受到重视。许多大中型桥梁上均布置了健康监测系统[7-9],诸多学者也将桥梁的损伤识别技术作为其研究方向[10-11],使得这一学科得到了飞速发展。现有的桥梁损伤识别方法往往仅能对其损伤位置进行确定,但对于损伤程度识别效果较差。
本文提出一种基于曲率模态曲线变化的损伤识别方法,利用桥梁损伤时其曲率模态曲线会产生畸变这一特点,以曲率模态参数指标为基础,对桥梁损伤前后其曲率模态曲线的变化进行研究。采用多项式拟合、BP神经网络拟合技术,根据桥梁受损后其曲率模态曲线畸变的大小来反向拟合出现的损伤位置和损伤程度。以一座简支桥为例,对其设定单损伤、多损伤工况进行研究分析,根据桥梁损伤后曲率模态曲线畸变产生的部位确定结构损伤位置,并以其曲率模态曲线的畸变大小来拟合桥梁损伤程度。由算例结果可知,对于实际工程中经常出现的小损伤工况,这一方法的识别效果较好,可为实际桥梁的状态监测提供参考。
1 受损结构的曲率模态曲线分析
1.1 曲率模态曲线理论
在结构的健康监测中,采用挠度仪、位移传感器等测试设备可测得结构各测点实时的位移、振动情况,通过综合考虑桥梁各测点某一时刻的位移φ(r)(r为梁体的测点),可得到结构整体的位移模态Φ[12],即
Φ=[φ(1)φ(2)φ(3) …φ(r) …φ(n-1)φ(n)]
(1)
式中:n为布置传感器的测点数量。
通过对各测点的位移φ(r)进行中心差分求值,得到对应的曲率模态ρ(r),即
(2)
式中:dr,r+1为测点r到测点r+1的距离;dr-1,r为r-1测点到r测点的距离。
综合考虑各测点的曲率模态ρ(r),梁整体的曲率模态振型P为
P=[ρ(1)ρ(2)ρ(3) …ρ(r) …ρ(n-1)ρ(n)]
(3)
对于梁式结构,当出现局部损伤时,其曲率模态振型曲线会呈现相应变化,如图1所示。
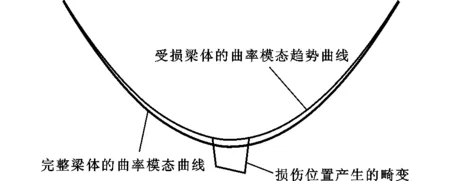
图1 梁体损伤时曲率模态曲线的变化Fig.1 Changes of Curvature-mode Curves in Beam Damage
1.2 曲率模态曲线的趋势变化
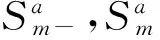
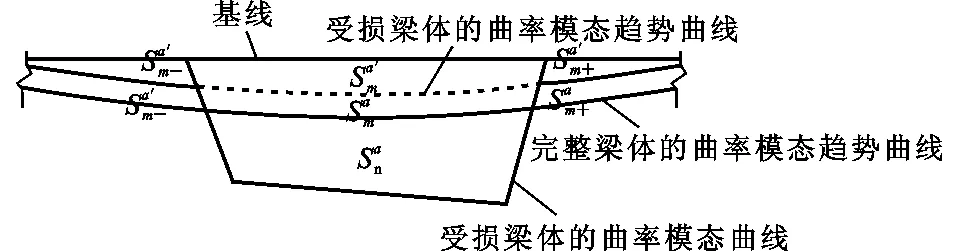
图2 整体曲率模态曲线的畸变面积Fig.2 Distortion Area of Holistic Curvature-mode Curve
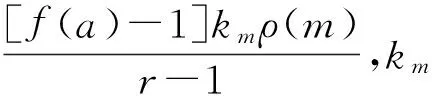
未损伤曲率模态曲线的面积SW为
(4)
损伤梁体的曲率模态曲线面积SS为
(5)
梁体损伤前后曲率模态曲线的面积差T(a)可表征损伤面积的变化情况,即
(6)
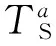
引入损伤梁体的曲率变化情况,化简可得曲率模态振型P(a)为
(7)
通过式(6),(7)可得到梁体相应工况下的损伤程度。
2 实例分析
选取一典型简支桥进行分析,其跨度为30 m,共等分为30个单元和31个节点。梁体左端N1节点和右端N31节点均为两端支撑。为研究受损结构曲率模态曲线的特征,设定下列损伤工况:16单元分别损伤5%,15%,40%,60%;11单元和21单元分别损伤10%,20%,45%和70%。
图3为简支桥在不同损伤程度下的一阶曲率模态曲线变化情况。表1为单损伤工况下简支桥的曲率模态曲线与横轴围成的面积,其中Si为i单元的曲率模态曲线与基线围成的面积,Si~j为i单元到j单元的曲率模态曲线与基线围成的面积,TS为所有单元的曲率模态面积和。表2为多损伤工况下模态曲线与横轴围成的面积。
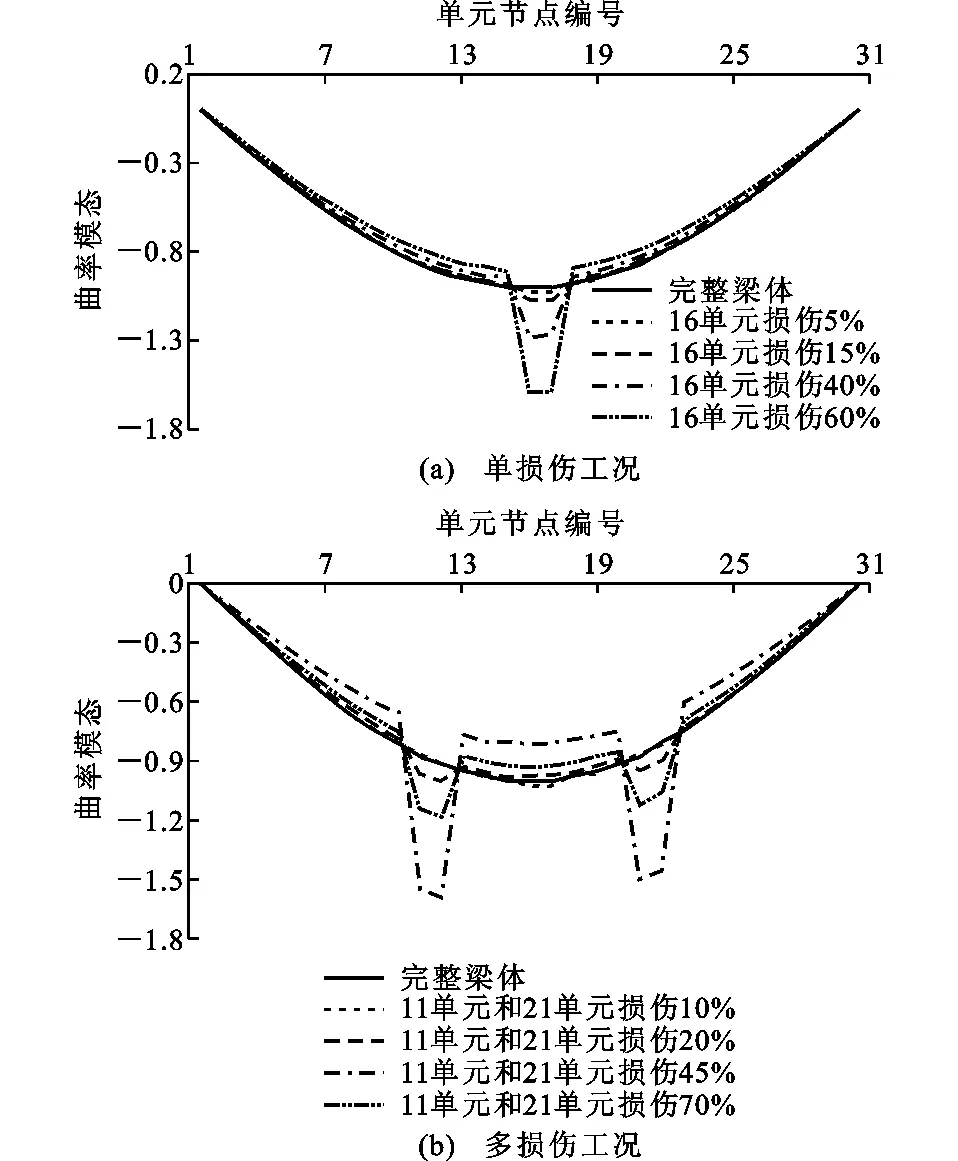
图3 简支桥的一阶曲率模态曲线Fig.3 First Order Curvature-mode Curves of Simply-supported Bridge
由表1,2可知,随着损伤程度的增加,受损单元的畸变面积随之增大,其他未损伤部位的面积呈现减小趋势。由T(a)的变化可知,随着损伤的加剧,总面积也呈现减小的趋势。

表1 简支桥在单损伤工况下的曲率模态曲线面积Tab.1 Curvature-mode Curve Areas of Simply-supported Bridge Under Single Damage Condition

表2 简支桥在多损伤工况下的曲率模态曲线面积Tab.2 Curvature-mode Curve Areas of Simply-supported Bridge Under Multiple Damage Conditions
3 损伤程度与面积变化的规律
通过上述实例分析可知,不同程度的损伤对应不同大小的畸变面积。根据损伤程度与面积这2类参数的变化规律,研究面积随损伤程度的变化,数据拟合是最好的方法之一[14]。目前常用的数据拟合方法主要包括线性拟合[15]、二次函数拟合[16]、多项式拟合[17]和神经网络[18-19]拟合方法等。本文仅对多项式拟合与神经网络拟合方法进行初步探讨。
3.1 多项式拟合方法
3.1.1拟合过程
假设分析的多项式为如下形式[20]
(8)
式中:yi为通过完整自变量计算得到的因变量;a0~ak为常数项;x为自变量;k为常数项项数;i为自变量项数。
对于式(8)中的多项式来说,自变量x的阶次为k,而精确计算这一阶次的多项式需要自变量x的个数为k+1,这样得到的拟合曲线可通过所有的数据位置。在实际的数据拟合分析中,往往通过仪器采集和计算分析只能得到自变量x的个数远远小于k+1。因此,采用这一方法进行拟合,存在数据误差d。
对于测点i有
(9)

因变量误差的平方和D为
(10)
误差平方和的展开多项式为
(11)
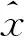

(12)
通过输入k+1组对应变量数据,可求得各自变量的待定系数a0,a1,a2,…,ak。在实际操作中,往往对应的变量数据输入组数m′=k+1,因此拟合多项式的阶次一般不宜取得过高。在m′7以后,矩阵出现病态,曲线震荡更加剧烈,因此本文研究中多项式的阶次取值不超过7。
3.1.2拟合效果
引入复相关系数r′的概念[21],它反映了一个因变量与一组自变量之间线性的相关程度,该指标的大小可等效表示线性关系的拟合效果,其计算公式为
(13)
利用复相关系数的大小可以在一定程度上衡量拟合效果[22-23],r′值越接近1,其拟合效果越好。r′的相关范围如表3所示。

表3 复相关系数r′的相关范围Tab.3 Correlation Range of Complex Correlation Coefficient r′
对于曲线拟合问题,这类非线性相关程度的求解可线性化是一种较好的方式[18]。通过变量代换将其转化成直线方程的形式,并根据直线方程求解未知量系数的方法求解系数,最后将直线方程还原成曲线方程。此类多项式为y=a0+a1x1+a2x2+a3x3+…+akxk,可令其高阶未知量转化为一阶未知量为x1=x,x2=x2,…,xk=xk。将多项式改写成y=a0+a1x1+a2x2+a3x3+…+akxk的直线方程形式,进而通过求解复相关系数r′确定非线性曲线的拟合效果。
3.2 神经网络拟合方法
利用BP神经网络进行数据拟合分为2个步骤:
(1)多组数据的训练、学习。首先选取具有代表性的多组数据自变量作为输入层样本进行输入,然后将数据的因变量作为期望输出进行设定。通过多组对应数据的学习训练,得到相应的隐含层神经元连接权系数,通过网络输出数据与期望输出数据的比较,进行隐含层相应参数的修改,使得实际输出和期望输出的误差达到最低,得到最优的BP神经网络模型。
(2)拟合应用。利用步骤(1)得到的BP神经网络模型,将待处理数据的自变量进行录入,通过神经网络的训练学习,得到较理想的输出因变量,即为BP神经网络进行数据拟合的过程。
3.3 损伤识别流程
根据上述2种拟合方法得到结构的损伤识别方法流程,如图4所示。
4 拟合验证
对上述简支桥实例进行验证,采用多项式拟合的方法进行曲率模态畸变面积与损伤程度关联性的验证。单损伤工况下的多项式拟合结果如表4所示。由表4可以看出,随着拟合次数的增加,复相关系数也呈现增大的趋势。当拟合次数达到3次以后,拟合基本达到了完全相关,因此采用多项式拟合的次数取3次,拟合效果如图5所示。
对损伤工况下面积的变化情况进行多项式拟合,得到对应的损伤程度为
a=3.045T3(a)+5.14T2(a)+
3.082T(a)-0.005 473
(14)
通过式(14)可计算该实例在单损伤工况下的损伤情况。多损伤工况下的多项式拟合情况如表5所示。从表5可以看出,随着拟合次数的增加,复相关系数也呈现增大的趋势。当拟合次数达到3次以后,拟合基本达到了完全相关,因此采用多项式拟合的次数取3次,拟合结果如图6所示。
对损伤工况下面积的变化情况进行多项式拟合,得到对应的损伤程度为
a=6.509T3(a)+9.575T2(a)+
4.554T(a)-0.008 099
(15)
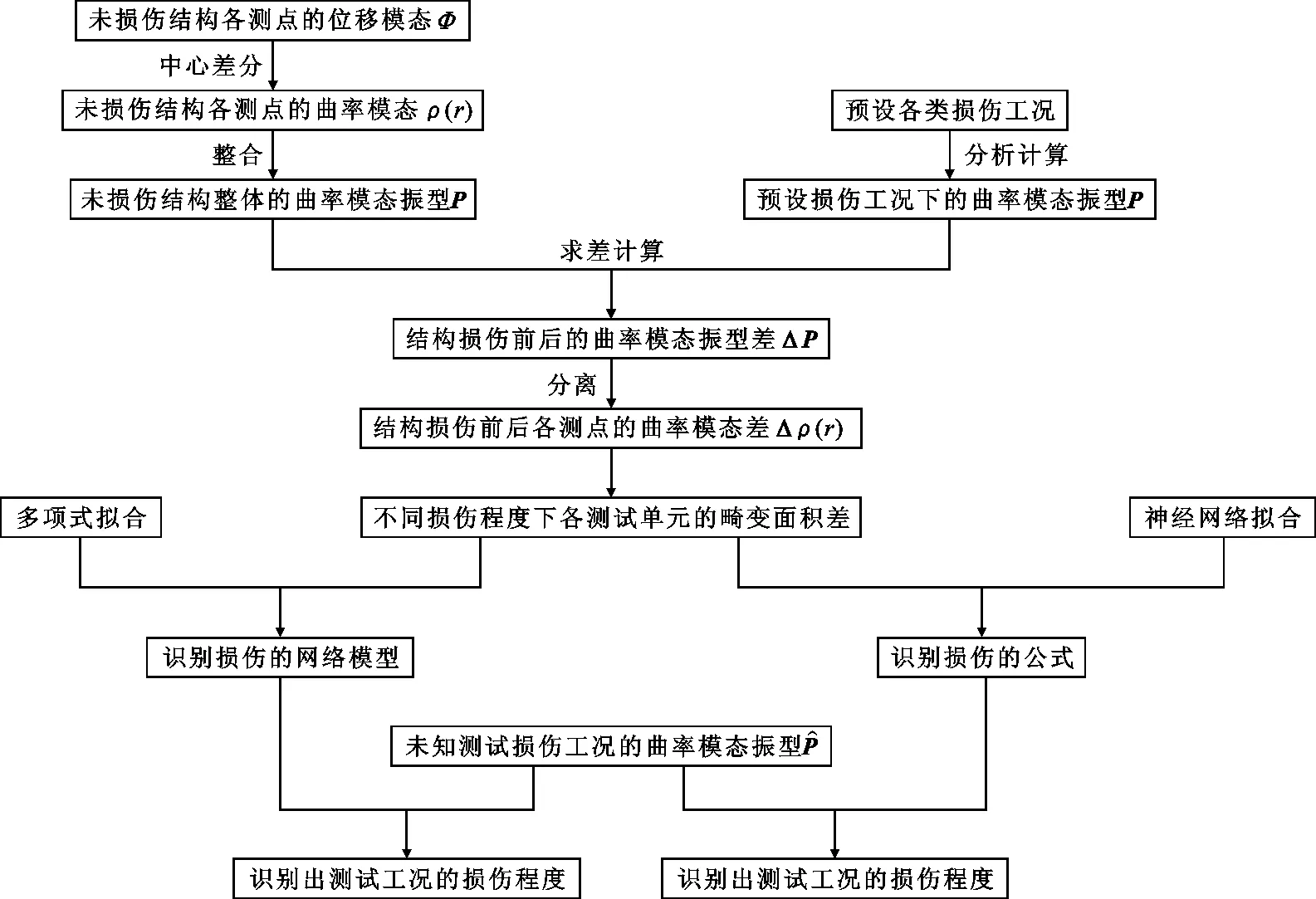
图4 损伤识别流程Fig.4 Damage Identification Process
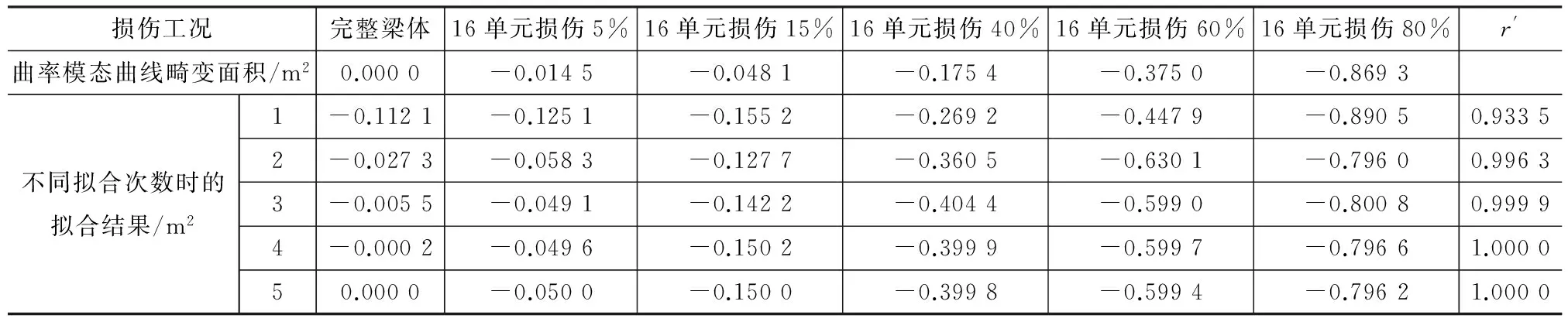
表4 单损伤工况下的多项式拟合结果Tab.4 Polynomial Fitting Results Under Single Damage Condition
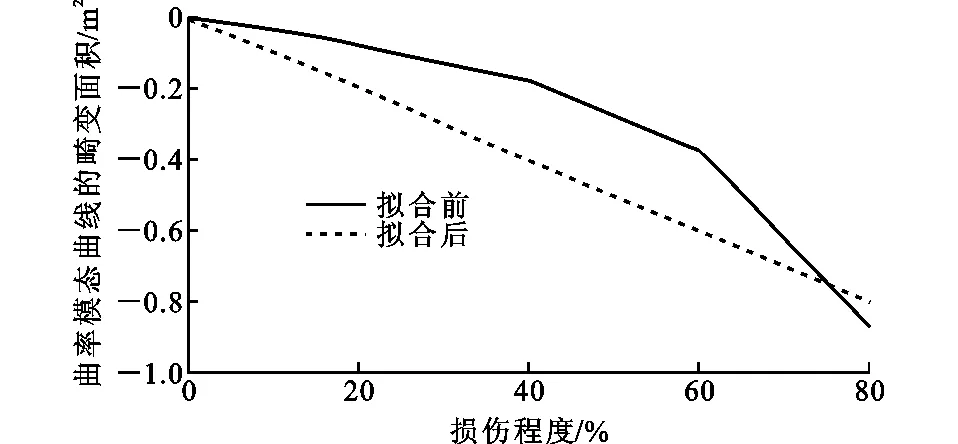
图5 单损伤工况下曲率模态面积的拟合结果Fig.5 Fitting Results of Curvature-mode Areas Under Single Damage Condition
通过式(15)可计算该实例在多损伤工况下不同损伤程度的损伤情况。
5 效果对比
设定下列损伤工况进行上述方法的验证:16单元分别损伤25%,50%,70%;11单元和21单元分别损伤15%,60%,80%。
单损伤工况下分别采用多项式拟合和BP神经网络拟合方法对不同程度的测试损伤工况进行识别,结果如表6所示。
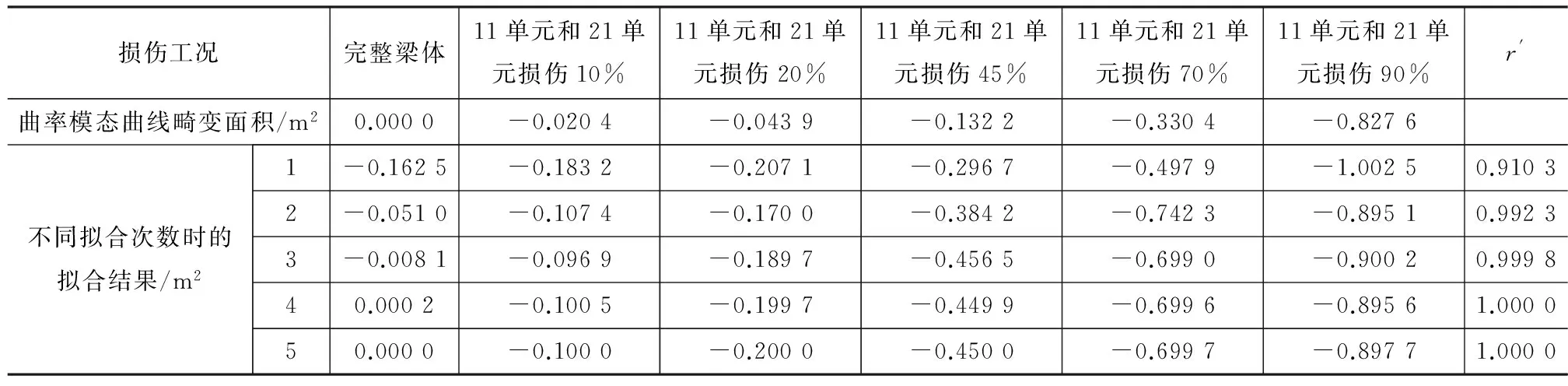
表5 多损伤工况下的多项式拟合结果Tab.5 Polynomial Fitting Results Under Multiple Damage Conditions
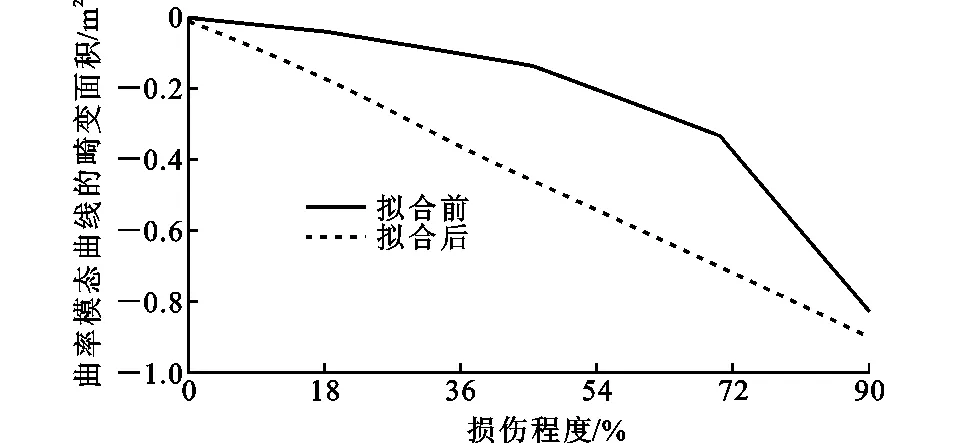
图6 多损伤工况下曲率模态面积的拟合情况Fig.6 Fitting Results of Curvature-mode Areas Under Multiple Damage Conditions
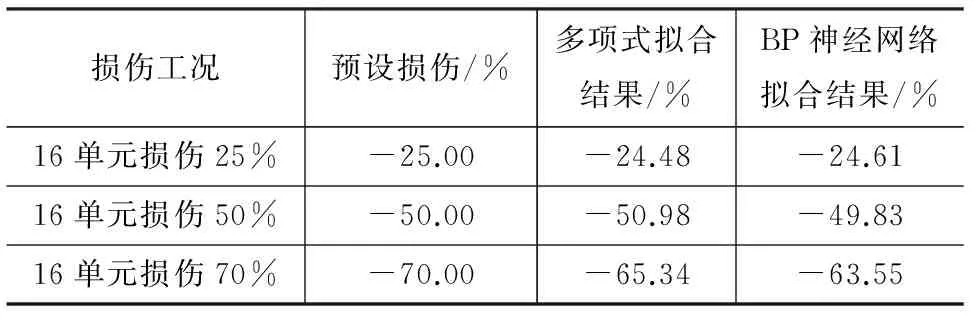
表6 单损伤工况下不同方法的损伤程度识别结果Tab.6 Damage Degree Identification Results of Different Methods Under Single Damage Condition
多损伤工况下分别采用多项式拟合和BP神经网络拟合的方法对不同程度的测试损伤工况进行识别,结果如表7所示。
由表6,7的识别结果可以看出,采用这2类方法都可以较好地对损伤程度进行识别。学习、训练数据的组数与识别精度关系较大,因此在实际操作中应尽量多选取数据组数进行学习与训练。本文实例中选取小损伤工况的训练数据较多,因此对于小损伤工况下损伤程度识别效果较好,而大损伤工况的识别效果较差。
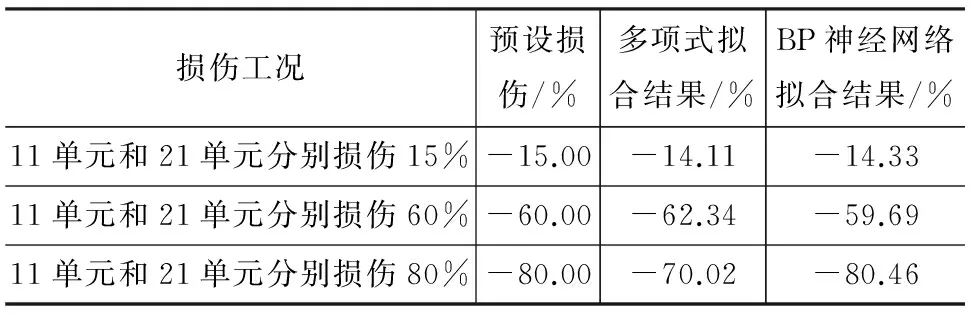
表7 多损伤工况下不同方法的损伤程度识别结果Tab.7 Damage Degree Identification Results of Different Methods Under Multiple Damage Conditions
6 结语
(1)本文以曲率模态参数为基础,提出一种基于曲率模态曲线变化的桥梁损伤识别方法。通过对桥梁损伤后曲率模态曲线的畸变面积进行反向拟合,可得到桥梁准确的损伤位置和损伤程度。
(2)桥梁损伤后,其曲率模态曲线产生的畸变面积与损伤程度存在正比关系,损伤程度越大,曲率模态曲线畸变面积越大。
(3)对桥梁损伤后曲率模态曲线的畸变面积进行研究分析,将畸变面积的变化趋势与损伤程度的发展进行拟合,可较准确地确定桥梁的损伤情况。
(4)通过多项式拟合得到的算式和BP神经网络的训练可对桥梁损伤情况进行定量分析。
参考文献:
[1]张连振,黄侨,郑一峰,等.桥梁结构损伤识别理论的研究进展[J].哈尔滨工业大学学报,2005,37(10):1415-1418,1441.
ZHANG Lian-zhen,HUANG Qiao,ZHENG Yi-feng,et al.Research State and Advances on Bridge Structure Damage Identification Theory[J].Journal of Harbin Institute of Technology,2005,37(10):1415-1418,1441.
[2]吴向男,徐岳,梁鹏,等.桥梁结构损伤识别研究现状与展望[J].长安大学学报:自然科学版,2013,33(6):49-58.
WU Xiang-nan,XU Yue,LIANG Peng,et al.Research Status and Prospect of Bridge Structure Damage Identification[J].Journal of Chang’an University:Natural Science Edition,2013,33(6):49-58.
[3]李冲,王克海,惠迎新,等.中小跨径桥梁地震作用下横向损伤模式分析[J].地震工程与工程振动,2015,35(3):125-133.
LI Chong,WANG Ke-hai,HUI Ying-xin,et al.Analysis of Transversal Seismic Damage Model Under Earthquake for Small and Medium Span Bridges[J].Earthquake Engineering and Engineering Dynamics,2015,35(3):125-133.
[4]LI J,HAO H,CHEN Z W.Damage Identification and Optimal Sensor Placement for Structures Under Unknown Traffic-induced Vibrations[J].Journal of Aerospace Engineering,2017,30(2):B4015001.
[5]唐浩,谭川,陈果.桥梁健康监测数据分析研究综述[J].公路交通技术,2014(5):99-104.
TANG Hao,TAN Chuan,CHEN Guo.Overview of Analysis and Research on Health Monitoring Data of Bridges[J].Technology of Highway and Transport,2014(5):99-104.
[6]王戒躁,钟继卫,王波.大跨桥梁健康监测系统设计构成及其进展[J].桥梁建设,2009,39(增2):7-12.
WANG Jie-zao,ZHONG Ji-wei,WANG Bo.Designed Components and Development of Health Monitoring Systems for Long Span Bridges[J].Bridge Construction,2009,39(S2):7-12.
[7]HEDEGAARD B D,FRENCH C E W,SHIELD C K.Time-dependent Monitoring and Modeling of I-35W St.Anthony Falls Bridge.I:Analysis of Monitoring Data[J].Journal of Bridge Engineering,2017,22(7):04017025.
[8]YU S,OU J P.Structural Health Monitoring and Model Updating of Aizhai Suspension Bridge[J].Journal of Aerospace Engineering,2017,30(2):B401 6009.
[9]陈国刚.二七长江大桥健康监测系统研究[J].中外公路,2014,34(1):170-174.
CHEN Guo-gang.Research on Health Monitoring System of Two-seven Yangtze River Bridge[J].Journal of China & Foreign Highway,2014,34(1):170-174.
[10]朱宏平,余璟,张俊兵.结构损伤动力检测与健康监测研究现状与展望[J].工程力学,2011,28(2):1-11,17.
ZHU Hong-ping,YU Jing,ZHANG Jun-bing.A Summary Review and Advantages of Vibration-based Damage Identification Methods in Structural Health Monitoring[J].Engineering Mechanics,2011,28(2):1-11,17.
[11]陈宇,李忠献,李宁.多介质体作用下近海桥梁的地震损伤分析[J].土木工程学报,2015,48(10):91-98.
CHEN Yu,LI Zhong-xian,LI Ning.Seismic Damage Analysis of Coastal Continuous Rigid-framed Bridges Considering Multiple Mediums[J].China Civil Engineering Journal,2015,48(10):91-98.
[12]张治国.基于模态分析理论和神经网络的桥梁损伤识别方法研究[D].武汉:武汉理工大学,2005.
ZHANG Zhi-guo.Research on Bridge Damage Identification Method Based on Modal Analysis Theory and Neural Networks[D].Wuhan:Wuhan University of Technology,2005.
[13]徐飞鸿,朱检,张婷婷.基于曲率模态曲线的结构损伤识别方法[J].世界地震工程,2015,31(4):36-42.
XU Fei-hong,ZHU Jian,ZHANG Ting-ting.A Method for Structural Damage Identification Based on Curvature-mode Curve[J].World Earthquake Engineering,2015,31(4):36-42.
[14]石振东,刘国庆.实验数据处理与曲线拟合技术[M].哈尔滨:哈尔滨船舶工程学院出版社,1991.
SHI Zhen-dong,LIU Guo-qing.The Technology of Experimental Data Processing and Curve Fitting[M].Harbin:Harbin Ship Engineering Institute Press,1991.
[15]何菊明,王芙.实验数据的线性拟合及计算机处理[J].武汉工程大学学报,2008,30(1):117-119,124.
HE Ju-ming,WANG Fu.Linear Fitting and Computer Processing on Experiment Data[J].Journal of Wuhan Institute of Technology,2008,30(1):117-119,124.
[16]PELLINEN T K,WITCZAK M W,BONAQUIST R F.Asphalt Mix Master Curve Construction Using Sigmoidal Fitting Function with Non-linear Least Squares Optimization[C]//TUTUMLUER E,NAJJAR Y M,MASAD E.Recent Advances in Materials Characterization and Modeling of Pavement Systems.New York:ASCE,2004:83-101.
[17]夏洪瑞,董江伟,邹少峰,等.常规二次多项式拟合地震数据[J].石油物探,2006,45(5):492-496.
XIA Hong-rui,DONG Jiang-wei,ZOU Shao-feng,et al.Normal Quadratic Polynomial Fitting Seismic Data[J].Geophysical Prospecting for Petroleum,2006,45(5):492-496.
[18]于柱春.基于BP神经网络的某型发动机万有特性实验数据拟合[J].山东交通学院学报,2012,20(2):21-25.
YU Zhu-chun.Universal Characteristic Experimental Data Fitting of a Certain Type of Engine Based on the BP Neural Network[J].Journal of Shandong Jiaotong University,2012,20(2):21-25.
[19]李俊益,陈启卷,陈光大.水轮机综合特性曲线BP神经网络拟合方法研究[J].水力发电学报,2015,34(3):182-188.
LI Jun-yi,CHEN Qi-juan,CHEN Guang-da.Study on Synthetic Characteristic Curve Processing of Francis Turbine Combined with BP Neural Network[J].Journal of Hydroelectric Engineering,2015,34(3):182-188.
[20]任雪娟,张耀存,马开玉.数值计算方法[M].北京:气象出版社,2007.
REN Xue-juan,ZHANG Yao-cun,MA Kai-yu.Numerical Method[J].Beijing:China Meteorological Press,2007.
[21]GERALD C F,WHEATLEY P O.应用数值分析[M].吕淑娟,译.北京:机械工业出版社,2006.
GERALD C F,WHEATLEY P O.Applied Numerical Analysis[M].Translated by LU Shu-juan.Beijing:China Machine Press,2006.
[22]张晓明.烟草主要化学指标与卷烟风格感官评价的修正复相关性分析[D].昆明:云南财经大学,2014.
ZHANG Xiao-ming.Correction and Complex Correlation Analysis Between Main Chemical Indexes and Sensory Evaluation of Cigarette Style[D].Kunming:Yunnan University of Finance and Economics,2014.
[23]王爱莲,史晓燕.统计学[M].西安:西安交通大学出版社,2010.
WANG Ai-lian,SHI Xiao-yan.Statistics[M].Xi’an:Xi’an Jiaotong University Press,2010.
