电磁感应与动力学综合问题探究

■江苏省响水中学　

处理电磁感应现象中的动力学问题的基本方法和思路是:先由法拉第电磁感应定律确定闭合电路中的感应电动势,再根据欧姆定律确定感应电流,然后根据F=BIL确定安培力,最后根据动力学运动规律(牛顿第二定律、动能定理、动量定理、功能关系等)求解相关动力学问题。

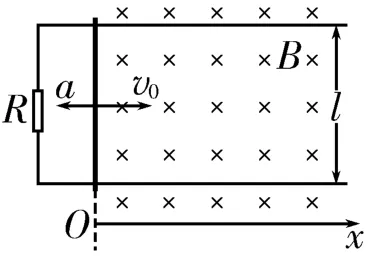
图1

例1 如图1所示,两条互相平行的光滑金属导轨位于水平面内,间距l=0.2m,导轨的一端接有阻值R=0.5Ω的电阻,在x≥0的范围内有一与水平面垂直的匀强磁场,磁感应强度B=0.5T。一质量m=0.1kg的金属直杆垂直放置在导轨上,并以v0=2m/s的初速度进入磁场,在安培力和一垂直于金属杆的水平外力F的共同作用下做匀变速直线运动,加速度a=2m/s2,方向与初速度方向相反。设导轨和金属杆的电阻都可以忽略,且接触良好。求:

(1)电流为零时,金属杆所处的位置。

(2)电流为最大值的一半时,施加在金属杆上外力F的大小和方向。

(3)保持其他条件不变,而初速度v0取不同值,求开始时外力F的方向与初速度v0取值的关系。

分析:金属杆在水平外力F和安培力的共同作用下做匀变速直线运动,加速度的方向向左。金属杆的运动过程为向右的匀减速运动→速度为零→向左的匀加速运动;判断外力F的方向需要先假设,再根据计算结果的正负号进行判断。

解:(1)金属杆切割磁感线产生的感应电动势E=Blv,感应电流,因为当I=0时v=0,所以m,即金属杆处于x=1m处。

(2)当金属杆的速度取最大速度v0时,金属杆中有最大电流;当金属杆中电流时,金属杆受到的安培力当金属杆向右运动时有F+F安=ma,解得F=0.18N,方向水平向左;当金属杆向左运动时有FF安=ma,解得F=0.22N,方向水平向左。

(3)金属杆刚开始运动时有v=v0,F安=,F+F=ma,解得F=安当时,F＞0,方向水平向左;当v0＞10m/s时,F＜0,方向水平向右;当v0=10m/s时,F=0,不满足题意。

以题说法:纯力学问题中只涉及重力、弹力、摩擦力,电磁感应现象中的力学问题比纯力学问题多了一个安培力,其处理方法与纯力学问题基本相同。此外,安培力的大小一般与导体切割磁感线的速度有关,当速度变化时,安培力也随之变化,从而使导体的受力情况(如导体的弹力和相应的摩擦力等)发生变化,而力的变化必然导致导体运动状态的变化。因此求解电磁感应现象中的动力学问题时,我们需要熟练掌握如图2所示的变化规律。

图2

例2 如图3所示,竖直放置的两根足够长的光滑金属导轨相距为L,导轨的上端分别与电源(串有一滑动变阻器R)、定值电阻、电容器(原来不带电)和开关S相连。整个空间充满了垂直于导轨平面向外的匀强磁场,磁感应强度为B。一质量为m、电阻不计的金属棒MN横跨在导轨上。已知电源电动势为E,内阻为r,电容器的电容为C,定值电阻的阻值为R0,不计导轨的电阻。

图3

(1)当开关S接1时,金属棒在磁场中恰好保持静止,则滑动变阻器接入电路的阻值R多大?

(2)当开关S接2后,金属棒从静止开始下落,下落距离s时达到稳定速度,则此稳定速度为多大?金属棒下落距离s所需的时间为多少?

(3)先把开关S接2,待金属棒达到稳定速度后,再将开关S接到3。试通过推导说明金属棒此后的运动性质,并求金属棒再下落距离s时,电容器储存的电能。(设电容器不漏电,且最终电容器没有被击穿)

分析:(1)当开关S接1时,金属棒在磁场中恰好保持静止,说明金属棒的重力与安培力平衡,由平衡条件和安培力公式列式,可求出电路中的电流,再根据欧姆定律可求出滑动变阻器a电路的阻值R。(2)当开关S接2后,金属棒从静止开始下落,先做加速度减小的变加速运动,待达到稳定状态后,再做匀速运动,根据重力的功率等于电功率列式可求出稳定速度,根据动量定理和法拉第电磁感应定律列式可求出时间。(3)金属棒达到稳定速度后,将开关S接到3,电容器开始充电,电路中有充电电流,金属棒受到安培力,根据安培力的瞬时表达式和牛顿第二定律可求得瞬时加速度,即可判断金属棒的运动性质。根据能量守恒定律可求出电容器储存的电能。

解:(1)当开关S接1时,金属棒在磁场中恰好保持静止,根据平衡条件得mg=BIL,又有,解得。

(2)当开关S接2后,金属棒达到稳定状态时做匀速运动,则,又有感应电动势E'=BLv,解得。根据动量定理得,又有感应电荷量,解得q=

(3)将开关S接到3时,电容器开始充电,电路中有充电电流,金属棒受到向上的安培力,设金属棒的瞬时加速度为a,根据牛顿第二定律得mg-BiL=ma,又有,得CBLa,即mg-BL·CBLa=ma,解得a=可见金属棒的加速度不变,即金属棒做匀加速直线运动。当金属棒再下落距离s时,设金属棒的速度为v',电容器储存的电能为ΔE,则根据运动学公式得v'2-v2=2as,根据能量守恒定律得,解得

以题说法:在匀强磁场中做匀速运动的导体棒受到的安培力恒定,可以用平衡条件进行处理;在匀强磁场中做变速运动的导体棒受到的安培力随速度(电流)的变化而变化,变速运动的瞬时速度可以用牛顿第二定律和运动学公式求解。在此类问题的求解过程中要画好受力图,并抓住a=0时,速度v达最大值的特点。若涉及始、末状态,以及力和作用时间,则用动量定理进行处理;若涉及始、末状态,以及力、位移和热量问题,则应尽量应用动能定理与能的转化和守恒定律解决。能量的转化和守恒是通过做功来实现的,安培力做功是联系电能与其他形式的能的桥梁,利用能量观点分析电磁感应现象中的能量问题,可以避开复杂过程细节的分析和变力功的计算。