带电粒子周期性侧移和回旋的场环境

■河北省廊坊市中国石油天然气管道局中学　

带电粒子在场中的运动,既有抛体运动,又有圆周运动,还能通过特殊的场环境对抛体运动和圆周运动进行转轨组合,实现周期性侧移和回旋,以综合力和能的知识全面考查中学物理知识,从而培养科学的物理思维方法。

1.组合磁场环境

例1 如图1所示,空间某平面内有一条折线是磁场的分界线,在折线的两侧分布着方向相反、与平面垂直的匀强磁场,磁感应强度的大小都为B,折线的顶角∠A=90°,P、Q是折线上的两点,且AP=AQ=L。现有一质量为m、带负电荷量为q的微粒,从P点沿PQ连线方向射出,不计微粒的重力。

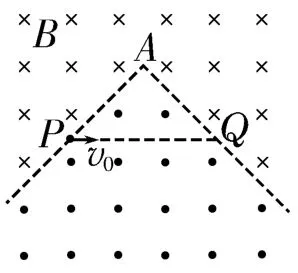
图1

(1)为使微粒从P点射出后途经折线的顶点A而到达Q点,求微粒的初速度应满足的条件。

(2)求(1)问中的微粒从P点运动到Q点所用时间的最小值。

解析:(1)要使微粒能从P点运动到Q点,则必须多次穿越两磁场分界线。因为两磁场的磁感应强度大小相等,所以由对称性可知,只要满足L=nx(n=1,2,3,…),其中x为每次偏转圆弧对应的弦长,n为PA或AQ边上的圆弧数。当n取奇数时,在PA边上的圆弧所对应的圆心角为,在AQ边上的圆弧所对应的圆心角为;当n取偶数时,在PA、AQ边上的圆弧所对应的圆心角都是如图2所示,设微粒的轨迹半径为R,由几何关系得,又有解得

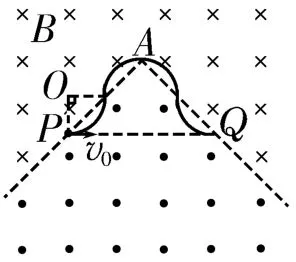
图2

(2)要使微粒从P点运动到Q点所用的时间最短,则需微粒从P点到Q点间的圆弧数最少,即n=1或n=2时即可。当n=1和n=2时,微粒从P点运动到Q点的偏转圆弧所对应的圆心角总和都为2π,故最小时间

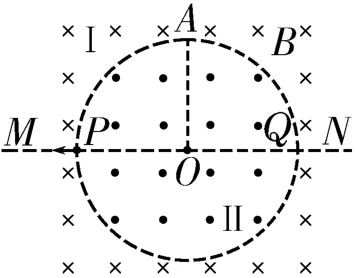
图3

例2 如图3所示,空间存在两个匀强磁场Ⅰ、Ⅱ,磁场Ⅰ足够大,与磁场Ⅱ的分界线是半径为R的圆周,磁场Ⅰ、Ⅱ的方向相反且垂直于纸面,磁感应强度大小都为B,水平直线MN过圆形磁场的圆心。现有一质量为m、带负电荷量为q的粒子从P点沿PM方向向左射出,不计粒子重力。

(1)若粒子在两个磁场中不断地飞进飞出,最后又能返回P点,求其返回P点的最短时间,以及粒子对应的速度。

(2)若粒子最终回到P点时的速度方向与从P点出发时的相同,求粒子的速度所满足的条件。

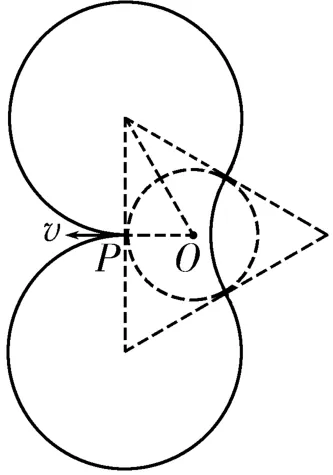
图4

解析:(1)根据题意可知,粒子从P点射出后,进、出磁场Ⅱ一次即返回P点所用的时间最短,轨迹如图4所示。设粒子的轨迹半径为r,由几何关系得,又有qvB=解得粒子在磁场Ⅰ中的两个回旋角都为300°,在磁场Ⅱ中的回旋角为60°,故返回P点的最短时间,又有T=,解得

(2)由(1)知粒子从P点出发每次进出两场,都在分界线上 “周期性侧移”一段弧长,粒子要能再次返回出发点,粒子经过两场分界线的穿越点需正好均分边界线。设各相邻穿越点与磁场Ⅱ的圆心O的连线间的夹角为α,则由周期性和对称特点得3,4,5,…),式中k可理解为从P点出发再返回到P点的过程中粒子在两个磁场分界线上完成的“周期性侧移”次数(等分数)。如图5所示分别为k=4,5,6粒子运动轨迹的情境。由几何关系知,又有qvB=,解得,且当k取偶数时,粒子返回P点时的速度方向水平向左,与出发时的相同。

点评:在组合磁场中,带电粒子通过周期性侧移完成周期性回旋。分析磁场的结构(如场的方向与大小关系、场边界的形状等)、画出粒子的运动轨迹示意图、确定一个侧移周期内粒子在磁场分界线(直线或圆)上发生的距离与轨迹半径的关系是解题的重要环节。

2.交变磁场环境

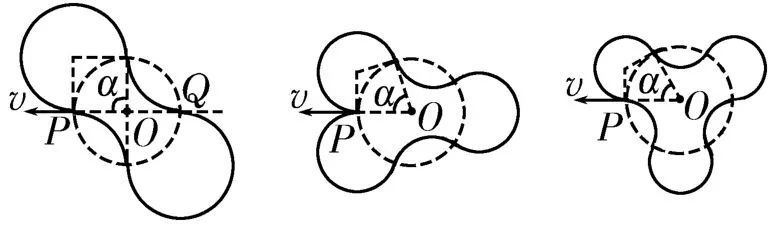
图5

例3 在直角坐标系xOy的第一象限(包括x、y轴)内存在磁感应强度大小为B0、方向垂直于xOy平面且随时间周期性变化的均匀磁场,磁场变化规律如图6所示,规定垂直于xOy平面向里的磁场方向为正。一质量为m、带正电荷量为q的粒子(重力和空气阻力均不计),从坐标原点O以某一速度v0沿x轴正方向垂直射入磁场中,经过一个磁场变化周期T0时间后到达第一象限内的某点P,此时粒子的速度方向恰好沿x轴正方向。

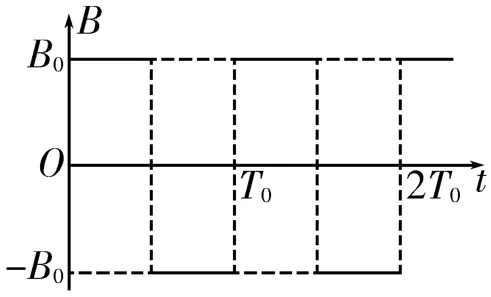
图6

(3)若粒子在t=0时刻以速度v0(已知)从O点射入磁场中,求粒子能够到达的P点纵坐标的最大值ymax和对应的磁场变化周期T0的值。

(4)若P点坐标为(d,d),要使粒子经过P点时的速度方向与OP连线成45°角,求满足这一条件的磁场变化的周期T0,以及粒子射入磁场时的速度v0。

解析:(1)设粒子在磁场中运动的周期为T,则,故当粒子在t=时刻从O点射入磁场中时,在随后的T0时间内粒子在y轴方向上的位移一定为零,粒子的运动轨迹如图7所示,则OP=4r,又有,解得P点的位置坐标为

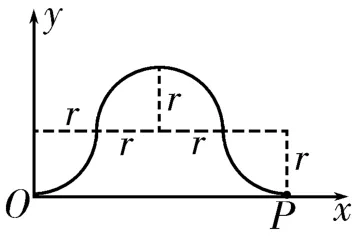
图7

(2)要使粒子必须从P点经过且速度方向总是沿x轴正方向,只要粒子发生如图7所示的周期性侧移即可,则d=n·4r(n=1,2,3,…),式中n为粒子在O、P两点间运动的等效周期数,又有,解得粒子速度的可能值v=0

(3)根据题意可知,要使粒子通过P点时的纵坐标值最大,其运动轨迹就必须尽可能靠近y轴,极限条件是与y轴相切,如图8所示。由几何关系得OO1=PO2=r,O1O2=2r,,故P点纵坐标的最大值ymax=OO1+AO1+从t=0时刻开始,粒子每转过α+90°=150°,磁场方向必须改变一次,即在磁场变化的半个周期内粒子转过150°角,则,解得

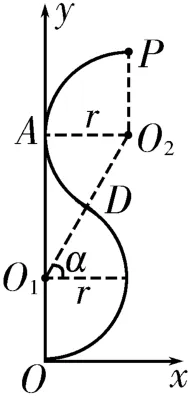
图8

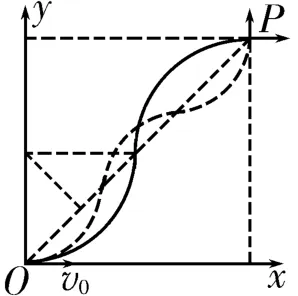
图9

(4)要使粒子经过P点时的速度方向与OP连线成45°角,须在磁场变化的半个周期内,粒子在磁场中旋转45°角,运动轨迹如图9中的实线圆弧和虚线圆弧。因为所以磁场变化周期。每一个圆弧对应的弦长,圆弧半径又有,解得v=0(n=1,2,3,4,…)。当n为奇数时,粒子经过P点时的速度方向沿y轴正方向;当n为偶数时,粒子经过P点时的速度方向沿x轴正方向。

点评:求解因磁场变化引起的周期性侧移和回旋问题,画出符合题意的运动轨迹示意图是突破难点的关键,确定磁场变化周期与粒子回旋周期的关系、粒子轨迹的圆弧弦长与侧移距离的关系是解题的两个重要途径,重视因时空周期性引起的系列解的取值是避免不完整解的有效环节。

3.中空磁场环境

例4 一个圆环形区域内有垂直于纸面向里的匀强磁场,内半径R1=1m,磁感应强度B=1T。一带电粒子从环心沿半径方向从中空区域与磁场交界面的P点以速度v0=4×107m/s射入磁场,粒子的比荷4×107C/kg,不计粒子在运动过程中的相互作用和重力。

(1)为约束该粒子不穿越磁场外边界,求磁场区域的最小外半径R2。

解析:(1)设粒子在磁场中做圆周运动的最大半径为R,则,解得R=1m。粒子的运动轨迹如图10甲所示,由几何关系得解得R2=(1+

(2)设粒子在磁场中运动的轨迹半径为r,则m。由几何关系得θ=30°,∠POP'=60°,故带电粒子进入磁场后每回旋240°又回到中空部分。粒子周期性回旋一周的轨迹如图10乙所示,故粒子从P点进入磁场到第一次回到P点,在磁场中的运动时间,在中空部分的运动时间,又有,所求总时间t=t1+t2=5.74×10-7s。

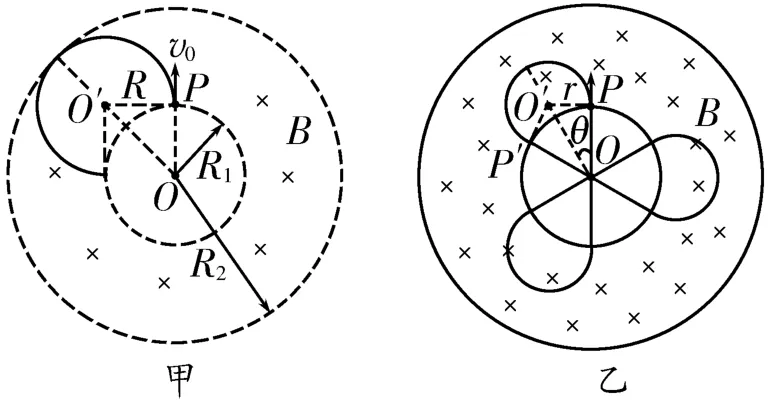
图10

点评:通过中空磁场实现带电粒子的周期性侧移与回旋,实质是通过无场区域让粒子做匀速直线运动来衔接两次相邻的圆周运动。重视空间对称性可有助于快捷分析此类问题。

4.电、磁复合场环境

例5 如图11甲所示,在xOy竖直平面内存在着与y轴平行的足够大匀强电场(图中未画出),现垂直于xOy平面加一足够宽的磁场区域,规定磁场方向向外为正,磁感应强度变化如图11乙所示,图中B0为已知量,t0、t1为未知量。一个质量为m、带正电荷量为q的小球,从t=0时刻开始,以初速度v0从坐标原点O沿直线OP方向运动,已知小球在以后的运动中能垂直于OP连线方向通过OP连线上坐标为(4L,3L)的D点,取g=10m/s2。求:

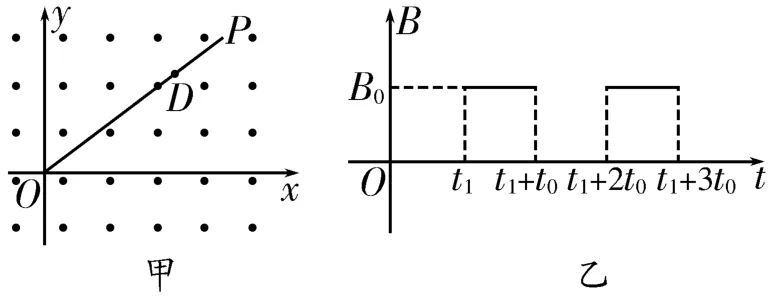
图11

(1)匀强电场场强的大小和方向。

(2)满足条件的t1表达式。

(3)通过进一步的研究发现,小球通过D点后的运动具有周期性,则此运动的周期是多少?

解析:(1)0～t1时间内无磁场,小球在重力和静电力作用下沿初速度v0方向做匀速直线运动,根据平衡条件得qE-mg=0,解得,方向竖直向上。

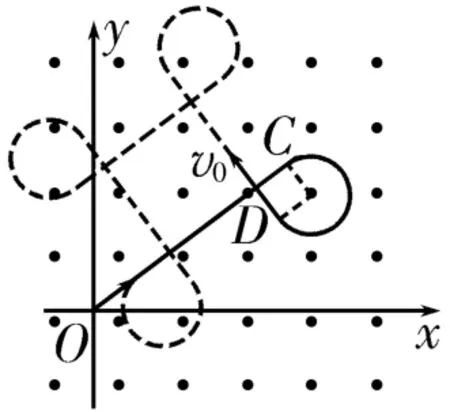
图12

(2)根据题意可知,要使小球垂直OP连线方向通过D点,只能让小球匀速直线运动到D点以后的某个位置C,再做匀速圆周运动并使其运动方向改变270°,然后沿直线运动经过D点,轨迹如图12中实线部分所示。设小球在磁场中运动的轨迹半径为R,周期为T0,由周期性特点可知,只要小球在洛伦兹力作用下的运动时间(n=0,1,2,…),就可垂直于OP连线方向通过D点,由图可知,C、D两点间的距离等于粒子做圆周运动的轨迹半径R。小球在t1时间内由O点匀速运动到C点的位移s=,故在t1～t1+t0时间内,小球在洛伦兹力作用下做匀速圆周运动,则,解得t=1

(3)小球做匀速圆周运动的周期T0=,由(2)知1,2,…),由磁场变化的周期性画出小球运动的轨迹如图12所示(包括实线部分与虚线部分),故小球做大回旋的周期

点评:对于通过电场和磁场组合的环境使带电体完成侧移或周期性回旋的问题,重视确定两场分界线处粒子的运动方向是重要的解题环节,灵活利用轨迹示意图展示的时空对称性是重要的解题工具。