三类辅助圆在临界问题中的应用
2018-04-08河南省淮阳第一高级中学
■河南省淮阳第一高级中学
求解带电粒子在有界磁场中运动问题的关键是正确分析出轨迹圆的临界状态,求出相应的临界条件。下面就来介绍三类辅助圆在临界问题中的应用,以期对大家有所帮助。
一、利用半径不同的放缩圆求解
当带电粒子的入射方向不变、质量一定而速度大小可变(速度不变而质量不同)时,粒子做圆周运动的轨迹圆心一定在表示粒子在入射点所受洛伦兹力的射线上,但位置不确定,画出半径最小(最大)的圆形轨迹,依据半径变化将圆放大(缩小),寻找圆周与磁场边界的切点,即可发现“临界点”。
例1 如图1所示,匀强磁场的磁感应强度为B,宽度为d,M、N为其左右边界。一电子从左边界垂直匀强磁场射入,入射方向与边界的夹角为θ,已知电子的质量为m,电荷量为e。要使电子能从磁场的右边界射出,求电子速度大小的范围。
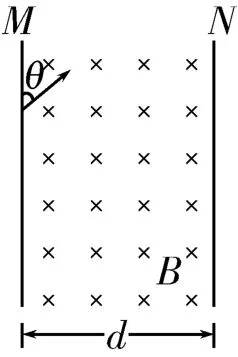
图1
解析:如图2所示,当入射速度很小时电子会在磁场中转动一段圆弧后又从同一侧射出;电子的入射速率越大,电子在磁场中的运动轨迹半径越大,当轨迹与边界相切时,电子恰好不能从磁场的右边界射出;当电子的入射速率大于这个临界值时,电子便从磁场的右边界射出。设此时电子的速率为v0,由几何关系得r+rcosθ=d。电子在磁场中做圆周运动时洛伦兹力提供向心力,则,解得r=。联立以上各式解得所以电子能从磁场的右边界射出的条件是入射速度大于
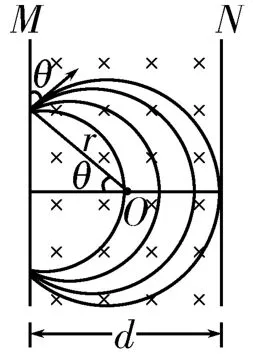
图2
点评:不断放大圆的半径,即可找出当电子的运动轨迹与边界相切时,电子恰好不能从磁场的右边界射出的临界条件。
二、利用半径相同的旋转圆求解
当带电粒子的速度大小不变而入射方向不同时,粒子做圆周运动的轨迹半径相同,但圆心变化。先画出粒子的某一特殊运动轨迹,按顺时针或逆时针旋转这一轨迹,从圆的动态变化中即可发现“临界点”。
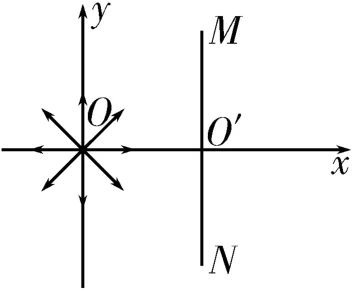
图3
例2 如图3所示,在直角坐标系的原点O处有一放射源,向四周均匀发射速度大小相等、方向都平行于纸面的带电粒子。在放射源右边有一很薄的挡板,挡板与xOy平面交线的两端M、N和原点O正好构成等腰直角三角形。已知带电粒子的质量为m,带电荷量为q,速度为v,MN的长度为L。
(1)若在y轴右侧加一平行于x轴的匀强电场,要使y轴右侧所有运动的粒子都能打到挡板MN上,则电场强度的最小值E0为多大?当电场强度为E0时,打到挡板上的粒子的动能为多大?
(2)若在整个空间加一方向垂直于纸面向里的匀强磁场,要使挡板右侧的MN连线上都有粒子打到,则磁场的磁感应强度不能超过多少(用m、v、q、L表示)?若满足此条件,放射源O向外发射出的所有带电粒子中有几分之几能打在挡板的左侧?
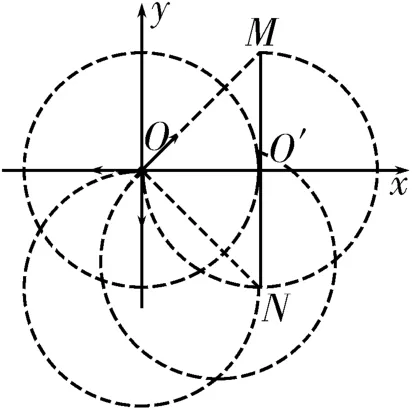
图4
解析:(1)要使y轴右侧所有运动粒子都能打在挡板MN上,其临界条件为沿y轴方向运动的粒子做类平抛运动,且落在M或N点。作动态圆如图4所示,则MO'=,解得由动能定理得,解得Ek=
(2)要使挡板右侧的MN连线上都有粒子打到,粒子运动轨迹直径的最小值为MN的长度L,则,解得B=0。放射源O发射出的粒子中,打在MN连线上的粒子的临界情况如图5所示。因为OM=ON,且OM⊥ON,所以OO1⊥OO2,v1⊥v2。故 放 射 源O发射出的所有带电粒子中只有能打在挡板的左侧。
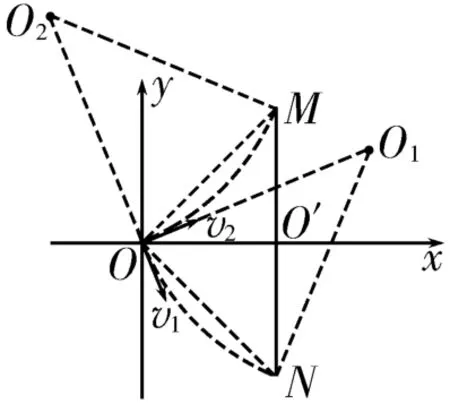
图5
点评:因为各带电粒子的运动轨迹半径相等,运动周期相等,所以各带电粒子运动轨迹的圆心分布在以粒子源O为圆心,R为半径的一个圆周上。
三、利用半径相同的平行圆求解
当带电粒子的速度大小不变及入射方向平行,且分布在一定范围内时,粒子在匀强磁场中做圆周运动的轨迹半径一定。先画出粒子的某一特殊运动轨迹,沿边界平移这一轨迹,从圆的变化中即可发现“临界点”。
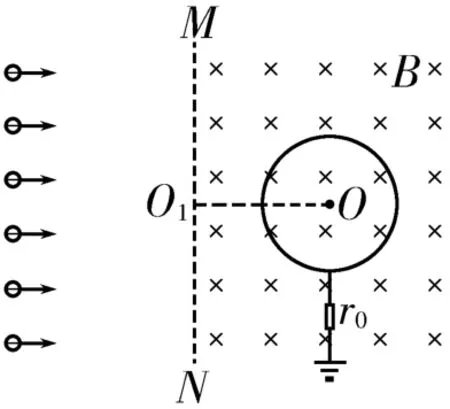
图6
例3 如图6所示,有界匀强磁场的磁感应强度为B,方向垂直于纸面向里,MN为其左边界,磁场中放置一半径为R的圆柱形金属圆筒,圆心O到边界MN的距离OO1=2R,圆筒轴线与磁场平行。圆筒用导线通过一个电阻r0接地,最初金属圆筒不带电。现有范围足够大的平行电子束以速度v0从很远处沿垂直于边界MN向右射入磁场区域,已知电子的质量为m,电荷量为e。(1)若电子的初速度满足,则在最初圆筒上没有带电时,能够打到圆筒上的电子对应边界MN上O1两侧的范围是多大?
(2)当圆筒上的电荷量达到相对稳定时,测量得到通过电阻r0的电流恒为I,忽略运动电子间的相互作用,求此时金属圆筒的电势φ和电子到达圆筒时的速度v(取无穷远处或大地电势为零)。
(3)在(2)的情况下,求金属圆筒的发热功率。
解析:(1)设电子进入磁场后的运动轨迹半径为r,则,解得r=3R。大量电子从边界MN上不同点进入磁场后的运动轨迹如图7所示,从O1上方P点射入的电子刚好与圆筒相切,则O1O2=同理得O1下方Q点到O1点的距离
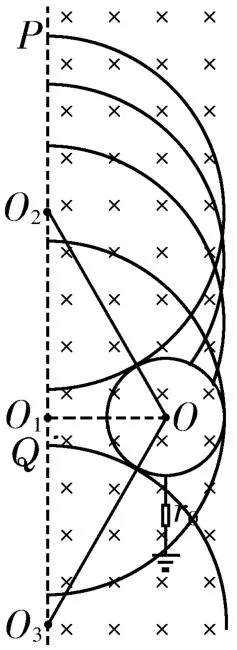
图7
(2)当圆筒上的电荷量达到相对稳定时,圆筒上的电荷不再增加,与地面的电势差恒为U,则U=Ir0,电势φ=-Ir0。电子在从很远处射到圆筒表面上的过程中,由动能定理得,解得
点评:求解这类问题需要抓住各带电粒子的两个特点,一是各粒子的圆形运动轨迹半径相等、运动周期相等,二是各粒子的圆形运动轨迹的圆心分布在同一条直线上。
