Stochastic Dynamic Modeling of Rain Attenuation: A Survey

Zhicheng Qu, Gengxin Zhang, Haotong Cao, Jidong Xie

1 College of Telecommunications and Information Engineering, Nanjing University of Posts and Telecommunications, Nanjing 210003, China

2 Satellite & Mobile communication Section, Nanjing University of Posts and Telecommunications, Nanjing 210003 China

3 National Local Joint Engineering Research Center for communication and network technology, Nanjing University of Posts and Telecommunications, Nanjing 210003 China

4 Key Laboratory of Broadband Wireless Communication and Sensor Network Technique of Ministry of Education, Nanjing University of Posts and Telecommunications, Nanjing 210003, China

I. INTRODUCTION

Satellite communication systems (SCS) play an indispensable role in the communication infrastructure, enabling communications in the regions where terrestrial wired or wireless networks cannot cover. In the past decades,numerous satellites have been launched, leading to spectral congestion of the conventional frequency bands allocated for satellite services, namely L (1/2GHz), S (2/4GHz), and C(4/6GHz) [1]. Meanwhile, to interface to backbone networks seamlessly with high data rate,the recent satellite applications are inclined to employ higher frequency bands to satisfy the growing capacity requirements. Therefore, frequency bands of Ku (12/14GHz), Ka(20/30GHz), and V (40/50GHz) have been equipped in modern systems.

However, according to the theory of radiowave propagation, 10GHz frequency is an upper bound that atmosphere physical phenomena become the dominant impairments to signal fading [2]. Moreover, R. Kaul [3] indicates that propagation effects can be categorized into two aspects: ionospheric effects and tropospheric effects. The former one influences systems operating below 3GHz, and the latter one influences those operating above 3GHz.For recent SCS operating above Ku band,tropospheric effects, i.e., rain attenuation,gaseous absorption, cloud attenuation, melting layer attenuation, sky noise increase, signal depolarization and tropospheric scintillations[1, 4-9], lead to 95% signal fading.

To counteract the propagation impairments,especially the rain attenuation (it results in a power loss in dB proportional to the square of frequency [10]), fade mitigation techniques(FMTs) are investigated and adopted by satellite operators.

Generally, the majority of FMTs perform the following process:

a) Use a constant sampling frequency at the receiver to measure the rain attenuation

b) Dispose the attenuation measurement and make short-term prediction of attenuation,which will happen at the next measurement interval

c) Re-con figure the system parameters i.e.,power, coding scheme, diversity etc. if necessary.

Short-term/real-time estimation of rain attenuation is a tough work due to the randomness of precipitation. Meanwhile, most of the channel prediction models are based on longterm or yearly averaged statistics. Therefore,to increase the efficiency and accuracy of FMTs, stochastic dynamic modeling (SDM) of rain attenuation is proposed.

Stochastic characteristics are the essence of the whole research field of communication and information. For instance, entropy, foundation of information theory, is de fined as a measure of the average uncertainty in the random variable, and a transmitting signal can be referred as a stochastic process. To study stochastic characteristics on communication systems,stochastic modeling (SM) is used to approximate systems under actual circumstances. For instance, in [11], SM is used to model cooperative multi-hop strip networks; [12, 13] utilize SM to characterize indoor wireless channels;[14] and [15] model cellular network with the stochastic geometry approach, which belongs to SM. SDM, which is also a branch of SM,focuses on enabling the effects of finite system response time to be calculated [16].

SDM based on stochastic differential equations (SDEs) aims to predict an accurate channel state in a short time slot since delay is a signi ficant factor in FMTs’ control loops. Each SDM owns a unique input parameter, which refers to a speci fic stationary rain attenuation distribution and uses this input to introduce the dynamic properties of rain attenuation into the model. This paper mainly summarizes different kinds of SDM currently in the literature.

The reminder of this paper is organized as follows. Section II provides the stochastic characterization of rain attenuation, including long-term rain attenuation analysis and dynamic properties. Meanwhile, this section puts emphasis on analyzing the initial dynamic stochastic modeling, (e.g. Maseng-Bakken model[16]). Section III provides the extensions of the original dynamic model of different types.These speci fic dynamic models cater to different climatic regions or FMTs. Section VI gives other approaches to generate rain attenuation time synthesizers other than SDE methods.Section V concludes the article and presents some thoughts about the future research on still unexploited aspects of rain attenuation time synthesizers.

This article carries out a survey of SDM using stochastic differential equations (SDEs) currently in the literature.

II. STOCHASTIC CHARACTERISTICS OF RAIN ATTENUATION

Rain attenuation predictions on satellite link can be divided into two parts: static attenuation predictions and the dynamics of attenuation process. [17] gives an overview of rain attenuation modeling approaches, where static prediction model bases on long-term analysis of rain attenuation and dynamic prediction model concerns the temporal rain process. The following of this section will illustrate those models in detail.

2.1 Long-term rain attenuation analysis

Due to the limitation of sampling and math methodology on modeling rain attenuation,long-term rain attenuation models based on observations or experiences were used in designing satellite systems. Those models can be categorized into two realms: 1) Focusing on the yearly average attenuation, usually based on the meteorological data over 20 years. L-W’s model [18], Lin’s model [19],M-H’s model [20] and EXCELL model [21]all belong to this part. 2) Offering the relation between rain-rateRand rain attenuationAand concerning about the frequency f, rain temperature, and raindrops size distributions [22]d.

In (1), a, b’, and cnare frequency, rain temperature, and parameters of a general drop-size distribution-based functions; d is a constant decided by drop-size distribution.

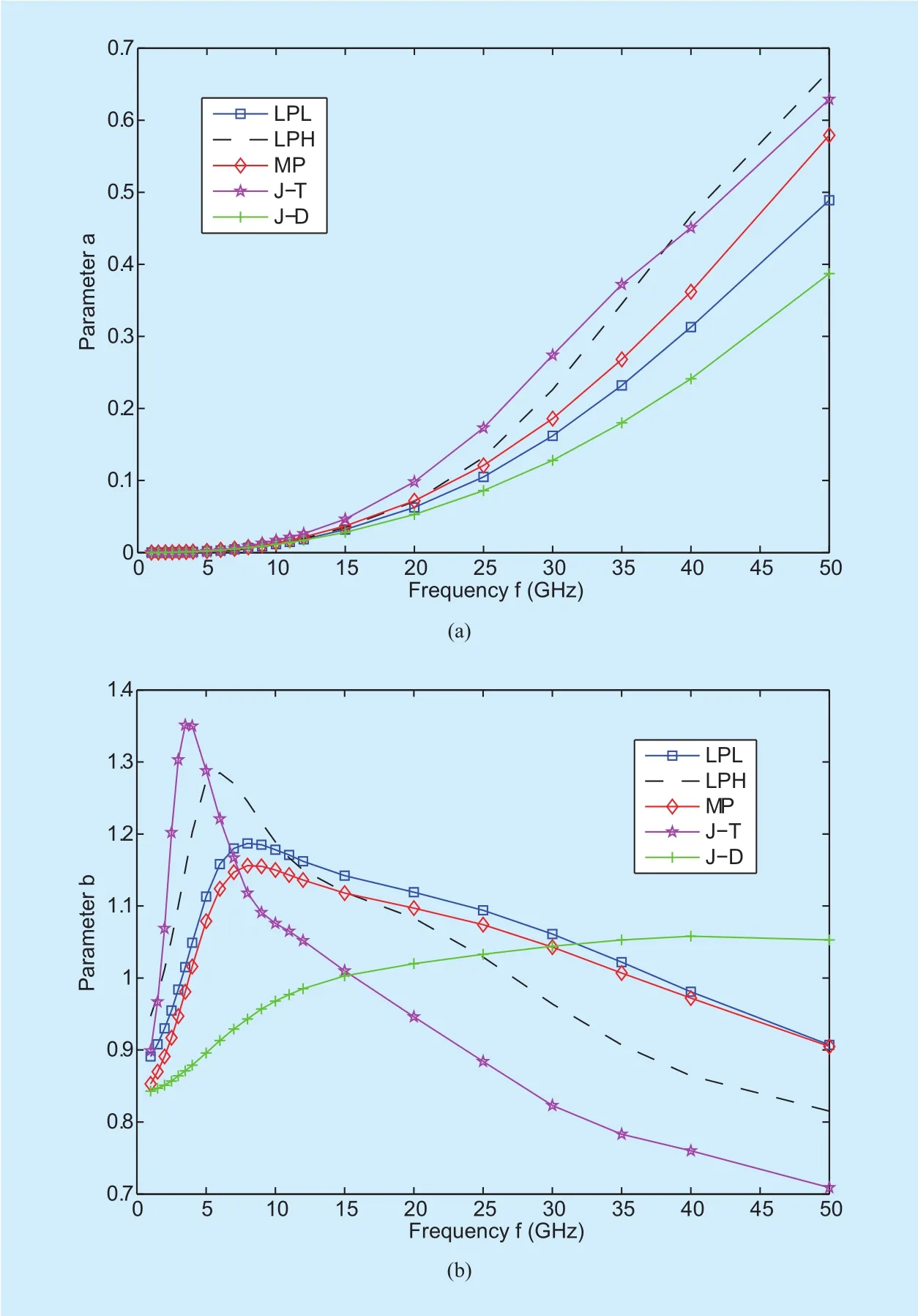
Fig. 1. Dependence of a, b in A= aRb on frequency and rain-drops distribution(data from [22])

In convenience of practical application, (1)must be simpli fied. As derived from [22], the approximate relation betweenAandRis:

This equation has been testified available of most practical interests, and makes it a very useful formula for calculation.

Previously, a and b are functions correlated to frequency, rain temperature, and raindrops size distributions. In Fig. 1 (a), dependence of a in (2) on above elements are depicted, where rain-drops distributions include Laws and Parsons (LP) distribution [23], Marshall-Palmer(MP) distribution [24], “Thunderstorm” Distribution (J-T) of Joss et al. and “Drizzle” Distribution (J-D) of Joss et al. [25]. To be noticed,the rain temperature taken into consideration is 0℃. Fig. 1 (b) focuses on parameter b, and the reminder of caption is the same as those in Fig. 1 (a).

2.2 SDM of rain attenuation

The main limitation of long-term modeling is that it cannot make response to the change of attenuation in a short time interval. However,modern SCS employing adaptive compensation techniques cannot tolerate the delay caused by long-term estimation of channel conditions. Thus, a group of SDMs based on SDEs is presented to generate the long-term rain attenuation time series with the M-B model [16] as initial.

According to [16], a relatively simple first-order Markov process was suggested to model rain attenuation, which bases on the knowledge of dynamic properties of rain attenuation at that time. The first-order process means that the statistics for future rain attenuation can be generated only depending on the current rain attenuation. Because the transition between rain periods and sunshine periods was not involved in the model, a Markov process with re flecting boundaries was used.

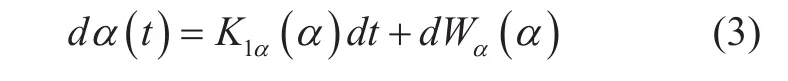
According to the knowledge of stochastic process and SDEs [26], rain attenuation process α(t) in M-B model is written as:in which Wα(α) is an independent incremental process with zero mean and K2α(α)dt as its conditional variance. K1αand K2αare deterministic functions of α corresponding to the first two conditional moments:

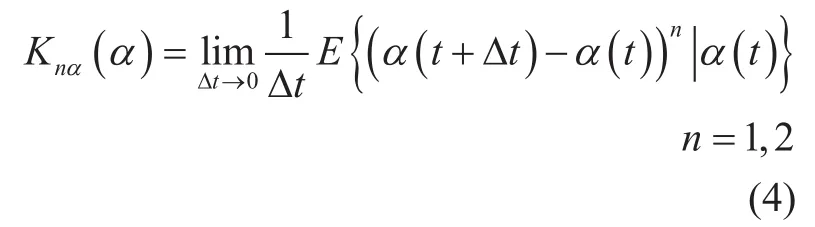
As shown above, K1αand K2αare the time-invariant drift and diffusion coefficients,respectively. Meanwhile, the probability density p(α,t) at these moments is given by Fokker-Planck equation [27]:

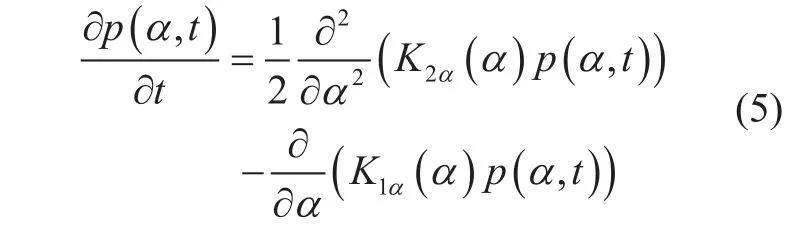
In [28], Lin proposed that the stationary probability distribution of α is lognormalwhere α is the median atmtenuation, and σαis the standard deviation of lnα.

Therefore, only one moment of the two is enable to characterize the process fully. [16]uses the transformation:

where β is the parameter of the modeling process changing rate due to the observation [29]which is proportional to α.

The former transformation enables α(t) to be replaced by:

then using Itô differential rules, (3) is turned into the linear SDE of Ornstein-Uhlenbeck type [30]:

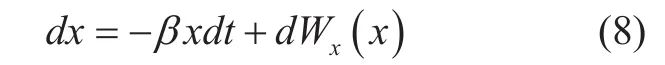
with Wx(x) an independent incremental process (zero mean and 2β as its variance). The probability density of x(t) in (7) satisfies the following stochastic differential equation:

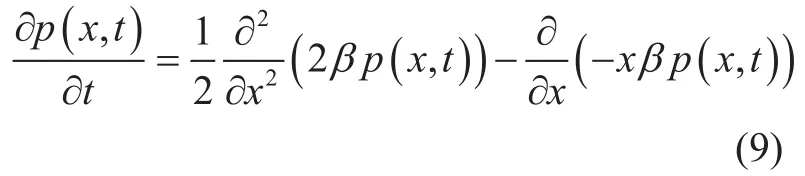
The complete dynamic solution of (9) for x results in the normal first-order stationary Markov process, and the conditional probability density of α(t) is a lognormal distribution:

The de finition of p1(·) and p2will be illustrated in the Appendix A.

Meanwhile, (2) indicates that the rain intensityRis lognormally distributed with parame-andR.

The stochastic dynamic model of rain attenuation generated from the white Gaussian noise is illustrated in Fig. 2. In this model,the system function of the low pass filter isand the memoryless non-linear device is derived from (7).

Additionally, in order to create full time series of rain attenuation, i.e., with both periods of rain and of no rain, a so-called enhanced M-B model (EMB model) was given in [31]and adopted by ITU-R for tropospheric attenuation time series synthesis [32], which improved the M-B model.

2.3 Dynamic Properties of the M-B Model

In M-B model [16], β is the parameter to represent the dynamic properties of the model such as the auto-correlation function and the fade duration statistics.

As first, the auto-correlation function is in the form of:

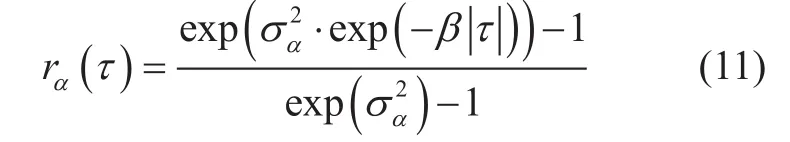
In addition, the values of different σαare shown in Table I.

As can be seen from the Table I, the correlation decreases with the increasing of σα,and this is coincident with (6).

As for fade duration statistics, from Fig.2, it is known that the fade threshold α0can be represented by x(t). Also, the statistics of the fade duration Txof the model are found from the level crossing properties of the Ornstein-Uhlenbeck process [30]. However, due tothe power spectrum of the Ornstein-Uhlenbeck process, the high frequencies carry extremely large power so that the average fade duration is zero. To solve the problem, in [16], bandwidth limitations in the level measurement filter is used to observe finite average fade duration statistics with the bandwidthωmis much larger than β. A certain measurement filter will lead to finite average, which depends on the threshold x0and the measurement bandwidth:

Table I. Auto-correlation function value.

Fig. 2. The stochastic dynamic model of rain attenuation [16].

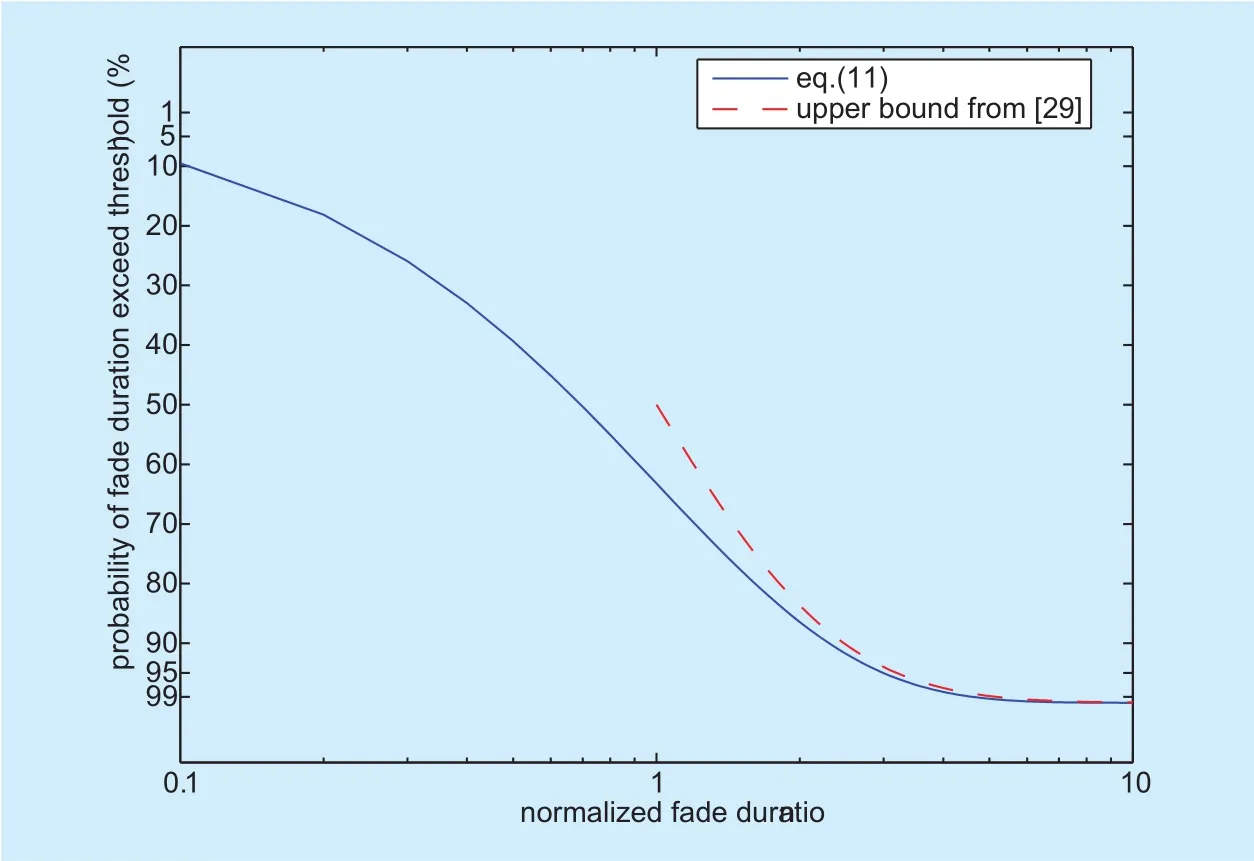
Fig. 3. Normalized fade duration distribution [16].

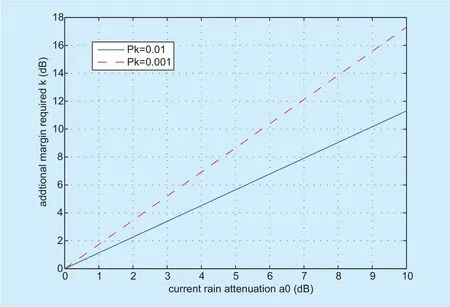
Fig. 4. Additional margin required with current rain attenuation α0.

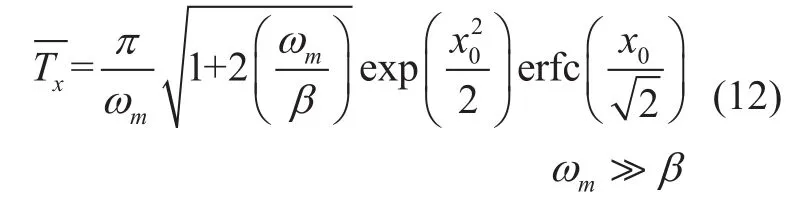
where erfc(·) is the complementary error function and the filter type is illustrated in[33].

The normalized probability distribution of fade duration is in form of:

Comparison of (12) and the upper bound of fade duration from [28] is depicted in Fig. 3.

One of the applications of the dynamic properties is to forecast the outage probability in the next ∆t seconds and then adjust the link margin k. The adjustments of different outage probabilities pkare shown in Fig. 4 (the ATS-6 in Austin, Texas with σα=1.38, ∆t=30s,and β=0.00185s−1). It can be seen from the figure that there is an approximate increase of 1.7dB (1.1dB) in link margin for each decibel increase in current rain attenuation when the outage probability of raining is 10-3(10-2).

III. EXTENSION ON M-B MODEL

In the previous section, the M-B model has three input parameters: two coincide with the distribution of long-term rain attenuation (in M-B model is lognormal distribution) while the third one represents the dynamic properties of the specific rain attenuation. [34] demonstrates a mathematical approach to calculate the dynamic input of a SDM so that the M-B model can simulate the hitting time (HT) sta-tistics simultaneously. Moreover, the stochastic properties of the first-order statistics, i.e.,the Cumulative Distribution Function (CDF)of the simulating rain attenuation process α(t),are not exclusively lognormal and different from area to area. To be more accurate, specific prediction of distributions will be made. Besides, the corresponding n-dimensional M-B model for diversity systems will be illustrated.

3.1 Calculation of optimum dynamic input of SDM

Generally, the dynamic parameter β in M-B model is either considered to be constant around 10-4Hz [31] or, it is calculated through both physical considerations and heuristic approaches. Particularly, the heuristic approaches consider that β should be calculated in order to simulate the second-order statistics of α(t).[35]¹ ensures the above suggestion by using Spectral Density Function (SDF) of the simulating process to approximate the actual rain attenuation’s SDF with the L1norm. However,in this approximation, some dynamic properties of the actual process cannot be reflected such as the HT statistics.

HT, as a second-order statistics of the rain attenuation, is de fined as the continuous time interval along which α(t) remains constantly above/below a given threshold Ath. Knowing a priori that at the start time t0the attenuation A( t0)=A0＞Ath, HTs are fully defined by the pair of (Ath, A0) [34]. In the original M-B model, HT statistics (i.e., the fade duration) is calculated in a measurement approach with a low pass filter (11). However, the first-order statistics of HT can be accurately analyzed with SDE knowledge. Using an infinitesimal generator [26] and the two coefficients of α(t),the moment generation function (MGF) of HT,i.e., the Laplace transform of HT’s probability density function (PDF) can be calculated. The theory of probability shows that the first derivative of a CDF is its corresponding PDF. Then,utilizing the Laplace transform (LT) and the inverse Laplace transform (ILT), the closed form of HT’s CDF can be solved for the triplet of parameters. Meanwhile, the mean value of HT can be also represented by (Amin,Amax,A0)while solving a nonhomogeneous boundary value problem. In M-B model, the triplet of parameters (Amin,Amax,A0) turns into(Amin,∞,A0), and the transformation (6) enables (Xth, X0) to simplify the boundary problem and represent the first-order statistics of HT. The detailed derivation will be illustrated in the Appendix B.

[34] also presents a group of pair properties of (Ath, A0) shown in Table II.

When the SDF of the simulated process and the normalized mean value of simulated HTs approximate the experimental (actual)ones simultaneously, then a SDE can simulate approximately both second-order and HT statistics of α(t).

The optimum value of β-1in Fig. 5 is an important supplement to the general M-B modelusing heuristic approaches to calculate the dynamic parameter.

Table II. The number of occurrence refer to the number of HTs events per pair(Ath, A0) [34].

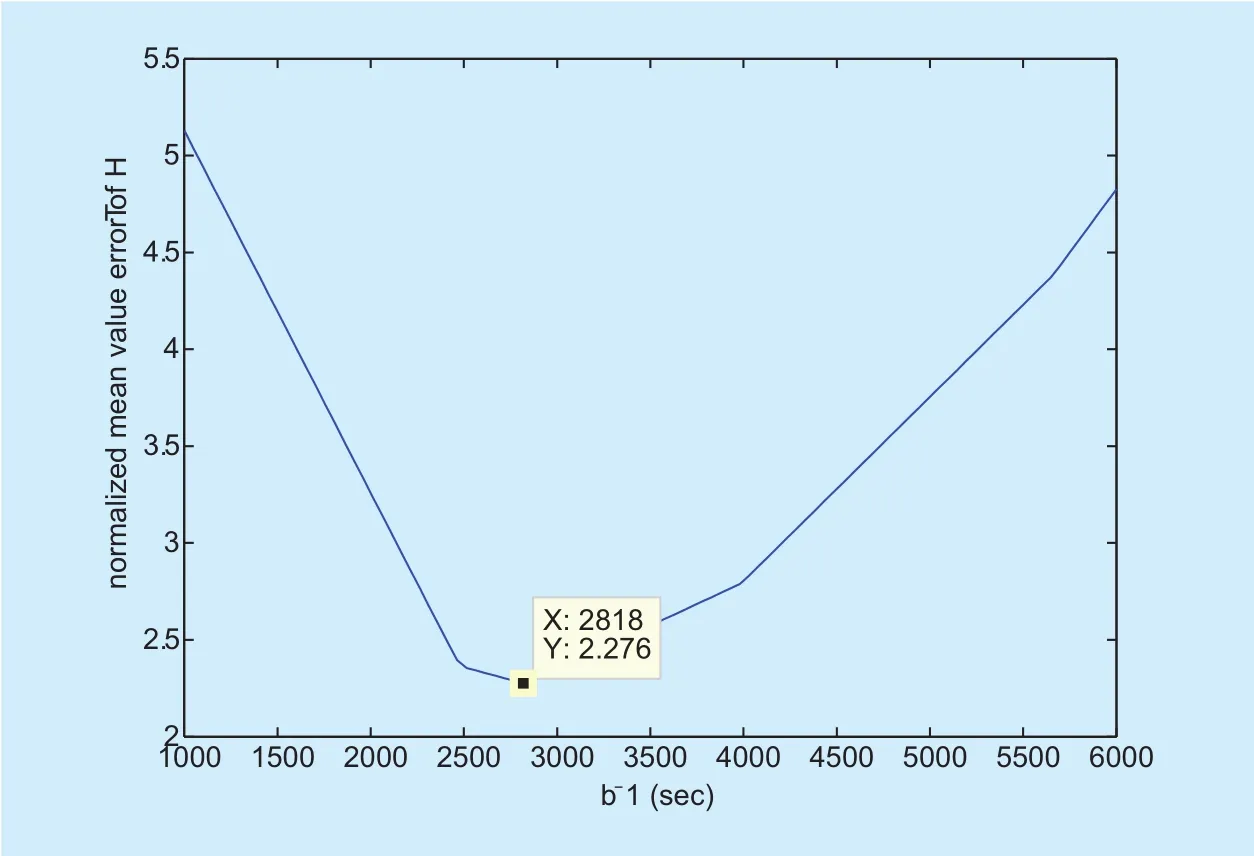
Fig. 5. Normalized mean value error of HTs (simulated/experimental) as a function of β-1[34].

3.2 Rain attenuation time series synthesizer based on diあerent distributions

The main focused climate area in the M-B and EMB model is the temperate zone, where lognormal distribution of rain attenuation is extensively tested and validated with the data from numbers of earth-space links.

However, the tremendous differences of rain rate and rainfall between different climate zones indicate that a universal distribution to generate the SDM is non-existent. Therefore,aiming at the speci fic properties of rainfall in local areas, researchers have proposed numbers of distributions of rain attenuation such as Gamma distribution (GD) [36, 37], Dirac and Lognormal distribution (DLD) [38], Weibull distribution (WD) [39], inverse Gaussian distribution (IGD) [40]. The advantages of those novel models will be illustrated next.

In heavy rain climatic regions, especially the tropics and sub-tropics, Gamma-distributed links are expected to perform better than the general M-B model [41]. [36] presents the block diagram of the Gamma model,which is similar to Fig. 2 except the expression of the memoryless non-linear devicehowever, does not have analytical expression for the Gamma distribution so that [42] provides MATLAB routines to get numerically implementation.This drawback has been eliminated in [37]5 by using the strong solution of SDE with GD inputs.

Besides the shortcoming of adopting lognormal distribution for CDF, [32] also has a limitation that a rain attenuation time series synthesizer, for worldwide applications, allows only exponential typed correlation function to be reproduced [38]. This is caused by the fact that those time series are modeled as a first-order Markov process so that the correlation function of rain attenuation is asymptotically exponential for small time lags regardless of the local climatology. Thus, [38]presents a novel model including rain and norain periods relied on a mixed DLD modeling and on a stochastic generation in the Fourier plane which allows any rain attenuation correlation function to be produced. This model utilizes a parameter P0as the probability to have rain attenuation on the link, and assume that only the rain attenuation conditional PDF is lognormal. Then, the absolute CDF of rain attenuation given as input parameter is represented by mixed DLD:

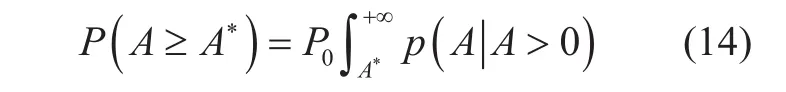
where A∗is the rain attenuation threshold and the integrand is the conditional lognormal PDF. As the model is to be worldwide applied,the corresponding stationary correlated Gaussian process is required to be regenerated.Therefore, a one-dimensional stationary real Gaussian process with zero mean, variance one, and arbitrary correlation function is constructed in the Fourier domain according to the following algorithm:

1) Generate an uncorrelated random complex number series (ek)k=0…N/2with length of N/2+1 with normal real and imaginary parts(zero mean and variance one). Meanwhile, for k = 0 and k = N/2, the imaginary part are put zero.

2) Span (ek) to N with the definition of

3) De fine coefficient hk=1/2 except for k= 0 and k = N/2 where hk=1.

4) Calculate the Fourier transform F(cG)from the analytical or numerical de finition of cGwhich is the correlation function of the Gaussian process.

6) Derive required Gaussian process Gj=F−1(ak) (F−1is the inverse Fourier transform), which eliminates the limitation of exponential de finition of cG(∆t ).

Additionally, [39, 43, 44] and [40, 45, 46]have recommended WD and IGD for the de-scription of rain attenuation’s PDF, respectively. In some cases, those two distributions possess potential superiorities to the original lognormal distribution. Moreover, the prediction method based on IGD for satellite terrestrial links has been developed not only for single links but also for route diversity systems [47,48], which caters to the modern FMTs in [1].

3.3 Multidimensional SDM application to earth-space diversity systems

Diversity protection schemes, which include time diversity (TD), site diversity (SD), frequency diversity (FD), and orbital diversity(OD), are countermeasures oriented against rain attenuation. Thus, they constitute the most efficient FMTs in terms of compensation of rain attenuation. For predicting rain attenuation on multiple links, the researchers from the Wireless and Satellite Communications Group, National Technical University of Athens (NTUA) [49] present a novel unified continuous model that can be considered as the n-dimensional generalization of M-B model, which can be referred as NTUA model for multidimensional application.

At the distances of interests in diversity systems, the spatial inhomogeneity of rainfall rate causes the correlation of rain attenuation values. [50, 51] prove the joint lognormal distribution is valid for calculating the long-term statistics of multidimensional rain attenuation.Therefore, the input of the model is a n-dimensional vector process of rain attenuation with each element lognormal. Comparing to the one-dimensional M-B model, the n-dimensional one has a corresponding covariance matrix C, which depicts the spatial correlation of rain attenuation, and the correlation coefficients in C can be calculated by the Paraboni-Barbaliscia model [52] for SD or the Lin’s model [19]for OD. Applying transformation (7) to each component process, the vector SDE is converted into its linear n-dimensional O-U type:

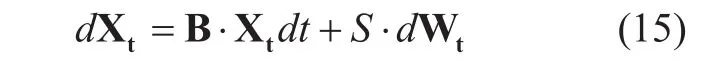
Corresponding to β in (8), the vector SDE has a diagonal matrixwhere δijis the Kronecker delta function. B captures the individual dynamic properties of each link depending on the elevation angle, the frequency, and the local climatic conditions [53]. Besides, a n×n matrix S is suitable for the linear transformation. [49] presents the derivation that each component process can be modeled independently to the corresponding 1-D case.

3.4 SDM for LEO satellite system

Low Earth orbit (LEO) satellite links, comparing to the geostationary link, have temporal changes in elevation angle. Thus, the SDM for LEO system will be time dependent, which different from the M-B model. In [54], the same group from NTUA establishes a model for LEO application scenario, which extends the M-B model to build a new SDM for LEO system. This model assumes that αm, σα, and β in M-B model are all functions of a speci fic elevation angle θ(t). β( θt) is the dynamic parameter of rain attenuation for a given moment. Meanwhile, it corresponds to an elevation angle of the LEO satellite channel at this time instant. A flow diagram of LEO links’rain attenuation time series is presented in figure 6. Comparing to the generation of original M-B model in figure 2, the LEO model only include extra calculation of time dependent elevation angle θt, and is similar to the derivation in M-B model on other parts.

IV. OTHER APPROACHES TO RAIN ATTENUATION TIME SERIES SYNTHESIZERS

4.1 Joint rain attenuation statistics in diversity systems based on copulas

In order to predict the outage probability due to rain attenuation of the diversity system, the joint exceedance probability of the rain attenuation is needed. Since the joint rain attenuation model is multivariate, Copulas [55] are used for modeling. Two advantages of Copulas [56,57] are that:

i) They could be employed without a parametric form, thus there is none assumption of specific distribution of the single site rain attenuation in advance.

ii) The models involve only one parameter to join

the multiple marginal distributions, called dependence index.

Meanwhile, the advantages of Copulas indicate that they can not only work for the SD system but also for other diversity systems such as TD system [57].

The basic theory of Copulas, taking bivariate scheme for example, is simply illustrated as follows:

1) Assume the CDFs of two variables X and Y are F(X) and G(Y), respectively.

2) There exists a copula function (CF)C(u,v) corresponding to the joint cumulative distribution H(x,y):

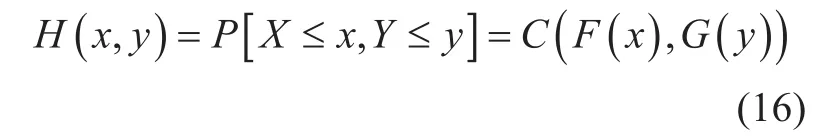
Transformations U = F(X) and V = G(Y)lead to random variables U and V, both uniformly distributed in the [0,1] interval. Mean-while, if marginal distributions F(X) and G(Y)are continuous, the CF is unique.

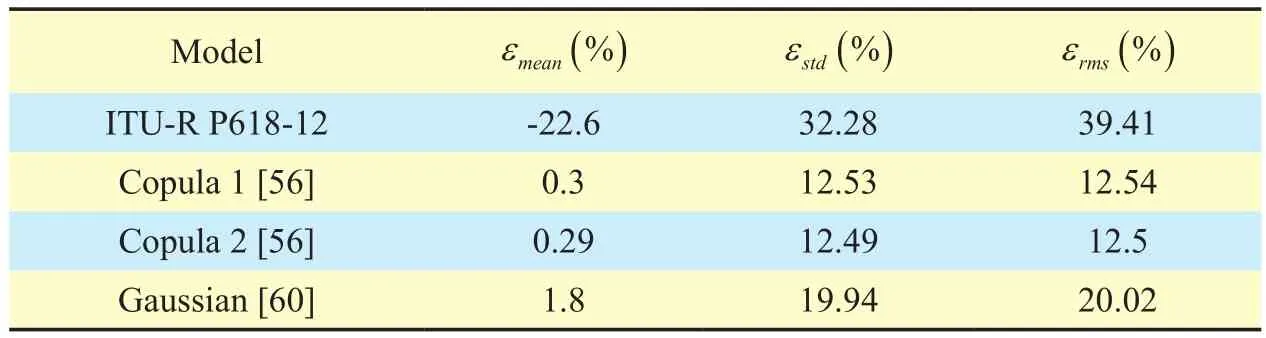
Table III. Error performance for evaluated copulas.

3) u and v are values of U and V, e.g. u =F(x). Therefore, the generalized inverse of a marginal distribution holds that F-1(u) = x, and so does v.

4) The joint exceedance probability in CF C(u,v) is as follows:

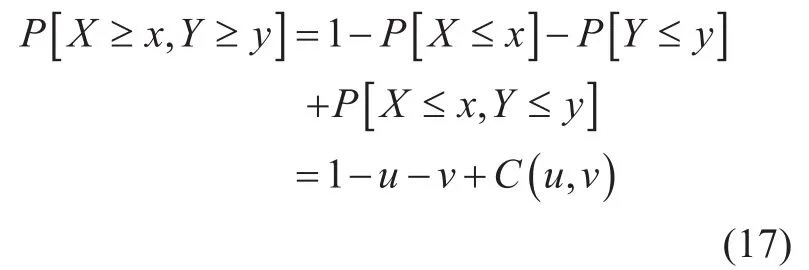
The properties of Copulas are that: ∀u, v∈[0,1]it holds that C( u,0)=0=C(0,v ), C( u,1)=u,and C(1,v)=v.

For joint rain attenuation statistics modeling, (16) is turned into

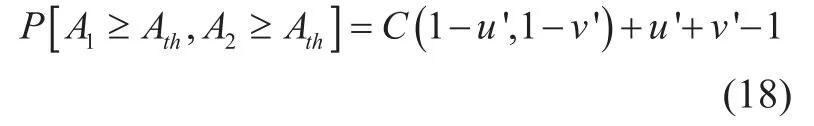
(18) is derived directly from (17) with u′=P[ A1≥Ath], v′=P[ A2≥Ath], and the property P[ X≤x]=1−P[ X≥x]. As can be seen from (17), since the single site CDFs of rain attenuation u’ and v’ are contained in the database of the ITU’s study group 3 (DBSG3)[58], the calculation of joint exceedance probability does not require any previous assumption of single site rain attenuation distribution.Comparing to the approach to calculate the outage probability P[ A1≥Ath,A2≥Ath] in[48] which have to calculate the integral of the bivariate IGD, the convenience using Copulas function is obvious. Turning the outage probability into P[ At≥Ath,At+∆t≥Ath], (17) is also able to be equipped in time diversity (TD) systems [57, 59].

Fig. 6. Flow diagram of the generation of LEO links’ rain attenuation time series [54].

To investigate which Copulas satisfy the experimental joint CDF of rain attenuation better, various CF categories such as Archimedean CF [56, 57] and Gaussian CF [59, 60] are used to make (18) fit to the experimental data for both SD and TD systems. Since CFs are non-linear functions, to derive parameter in the CFs and calculate the joint CDF of rain attenuation, a non-linear regression process is used.This method based on Gauss-Newton method was illustrated in [61, 62]. After choosing the potential Copulas by their regression to the experimental data, the error analysis including the mean value, the standard deviation and the root mean square (rms) values of the error are then produced to pick up the most accurate ones. Comparing to the ITU-R model, those CFs have better performance in every index above, and the results are shown in Table III.

Particularly, it must be noticed that the dependence index in the CFs can be simply defined as functions of separation distance (SD)[63] and time delay (TD), which are depicted in Fig. 7. It has to be emphasized that those parameters are not the strict correlation coefficients of the random variables but the strength of their dependence.

4.2 Rain attenuation statistics on mobile satellite links

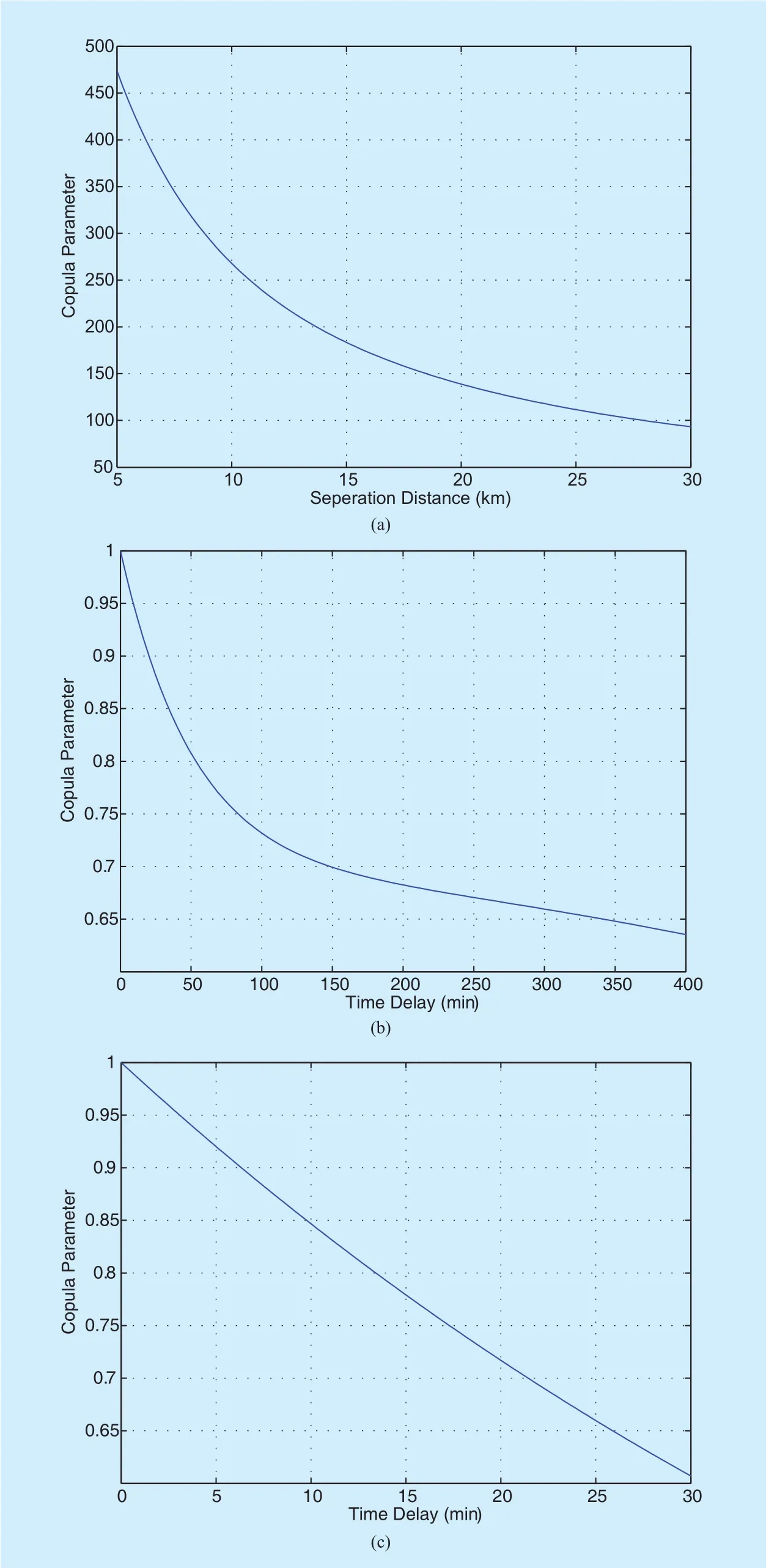
Fig. 7. (a) Archimedean CF parameter corresponding to separation distance for SD system, the range of distance referring to [63]; (b)(c) Gaussian CF parameter corresponding to time delay for TD system in temporal and tropical region, respectively.

Fig. 8. Velocity vectors and [65].

Land mobile satellite systems (LMSS) are widely used in satellite communication.Whereas, being different from the fixed satellite links, terrestrial LMSS are often able to exploit relatively strong multipath, and LMSS will be power limited and dependent on the line-of-sight (LOS) signal component [64]. In terms of rain attenuation, the statistics such as fade duration and changing rates in LMSS may be larger or smaller than that in the fixed system, depending on the relative speed between vehicle and the rainstorm. Thus, [65]proposed a transformation to build LMSS rain attenuation statistics based on those in fixed systems. This transformation relates to the hypotheses that the slant path with elevation angle θ is a geostationary satellite link, the speeds of vehicles and rain storms are constant vM, vR, respectively, and the “synthetic storm technique” can be applied. The hypotheses hold that the conditional probability distributions of αMand αFfor mobile and fixed rain attenuation, respectively, would be identical.However, those referred to a fixed interval(e.g., the measuring duration of rain attenuation) would be different due to the difference of time scales between αM(t) and αF(t).Therefore, calculation of fade duration in LMSS is important to the transformation.

Fade duration in fixed system TF(e.g., the time storm takes to pass over the fixed terminal) is given by

Where DRis the radius of the rain area “seen”by a fixed rain gauge, and LFis the projection of the slant path L to the satellite at ground and along the direction of the storm motion.Correspondingly, TMis given by

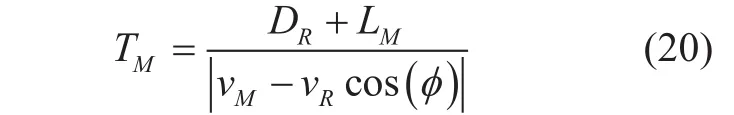
Noticing that 0≤LF,LM≤Lcos (θ),and the value of elevation angle θ makes LF,LM≪DR, the relationship between TFand TMis

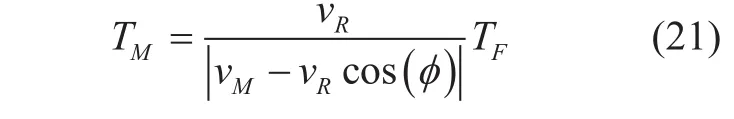
However, αM(t) and αF(t), compared to each other, are linearly distorted due to the relative motion of rainstorm and vehicle.Hence, the former ratiobetween TMand TFis the relationship between of the CDFs PM(α) and PF(α),The upper bound of ξ is 1/PF(α) due to the property of CDF. As for second-order statistics, there is

V. CONCLUDING & FUTURE RESEARCH PERSPECTIVES

Fade mitigation technology (FMT) is a promising approach to overcome the rain attenuation attached to the satellite links. Stochastic dynamic modeling (SDM) is the fundamental of FMT to estimate the real-time properties of rain attenuation process. There have been numerous kinds of SDMs with the Maseng-Bakken (M-B) model as initial. Those kinds of SDMs can represent both first-order and second-order statistics of rain attenuation while the former long-term model can only calculate the first-order ones.

This paper makes a survey on some of the existing SDMs and the extending approaches to calculate the dynamic properties of rain attenuation. In this paper, the M-B model and the extension of M-B model are summarized in more detail. In addition, other aspects of rain attenuation statistics are also introduced.

For future work of SDMs of rain attenuation, this section highlights the future directions and two main fields are mainly identified:

5.1 Implementation of SDM

Initially, it is to the different distributions based SDMs. For instance, [36] has proven the better attenuation rms error of Gamma distribution based SDM than the EMB model (lognormal distribution based) proposed by [31].However, the attenuation rms error of Scania link (Sao Paulo, Brazil) [36] is 0.03 larger than the corresponding value calculated by EMB model. The same situation exists in all other distribution-based SDMs due to the limited simulations. Therefore, a further exploration is necessary. The following work in this aspect is to make a SDM satisfy to all conditions in a single area.

Then, it is to the study of Copulas. First and foremost is the analysis of the copula parameter belonging to the selected copula functions.Those parameters are functions of separation distances or time delays in SD systems and TD systems, respectively. [56] recommended that the proposed estimation of CF parameters would be better used with precaution.Further experimental verification is required to calculate the CF parameters in various climatic regions, where geometrical and system characteristics are different. Besides, due to the essence of approximation for CF methods, the performances of different CFs must be enhanced by additional validations and comparisons to ITU-R model by a number of new experiments. This is the key point for CF methods and worthy deeper study.

5.2 Mobile application of SDM

To the mobile application of SDM, [65] has proposed a transformation to convert fixed rain attenuation statistics into the corresponding mobile ones. Since the transformation only focused on the long term statistics, to the next stage, [65] needs to complete the transformation combining the utilization of SDM.What’s more, the speci fic relationship between the dynamic properties and the velocity of mobile terminals can be investigated. This can strength and optimize the accuracy for mobile application of SDM.

Next, it is the aspect of communication between LMSS and LEO satellite. In the future, this kind of satellite communication will become the mainstream. Though [54] has proposed the SDM for LEO satellite, it was still based on the fixed land terminals. For LMSS,the dynamic elevation angle function θ(t),which need to take rolling compensation of mobile platform into consideration, is much more complicated. Therefore, further calculation of the dynamic elevation angle with efficient targeting algorithm will eventually make SDM application in LMSS-LEO communication effective.

ACKNOWLEDGEMENTS

The authors would like to thank the reviewers for their detailed reviews and constructive comments, which have helped improve the quality of this paper. This work is supported by the National Natural Science Foundation of China (Grant No.91338201).

Appendix A

The lognormal distribution has the form of

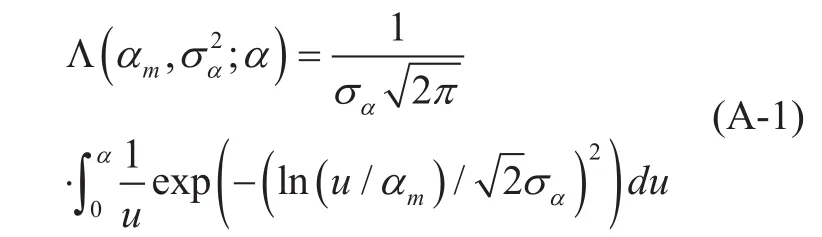
p1(·) and p2in (9) are expressed by

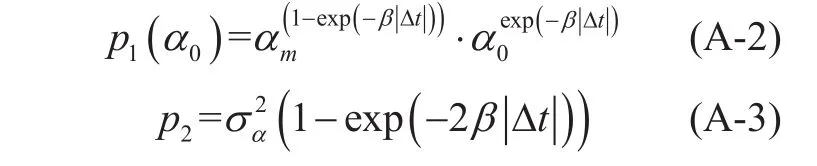
Appendix B

(Xth, X0) corresponds to the input (Ath,∞,A0)in M-B model, and the moment generation function (MGF) is

where

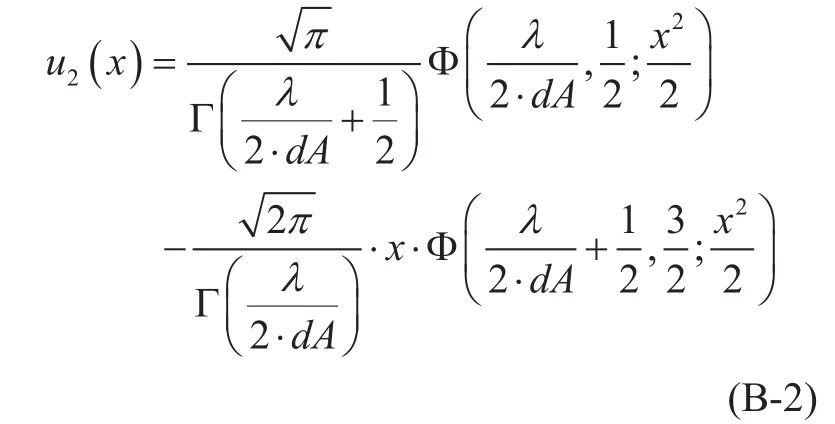
and Φ(a, b; x) is the Kummer’s Function. The mean value is given by

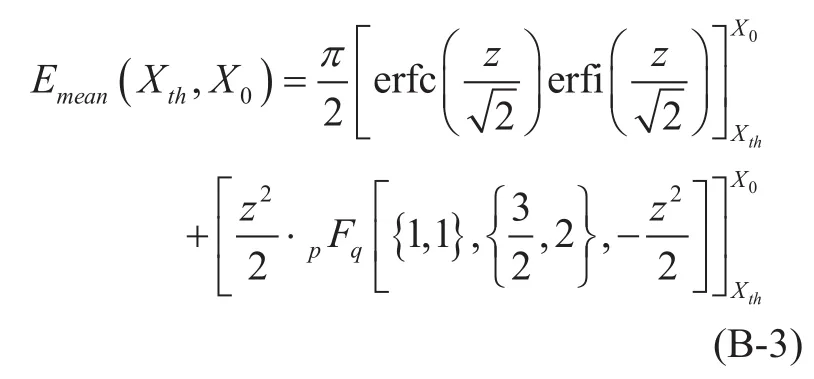
For the functions erfc(·) (complementary error function), erfi(·) (imaginary error function), andpFq, see [66].

Appendix C

Archimedean copula functions:

Copula 1 (Clayton copula):

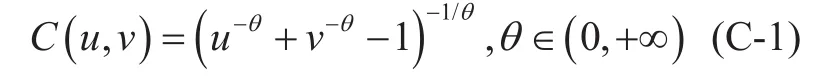
Copula 2:

Copula 3:

Copula 4:

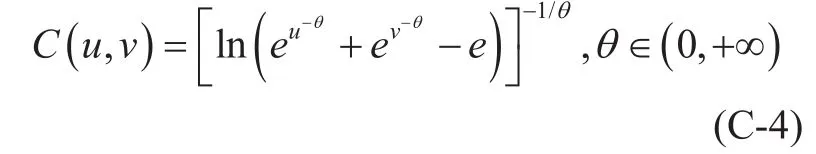
Where

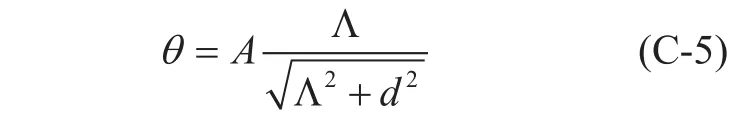
A, Λ are two parameters corresponding to the selected CF, and d is the separation distance of the two Earth stations expressed in km.

And Gaussian copula in case of two random variables is

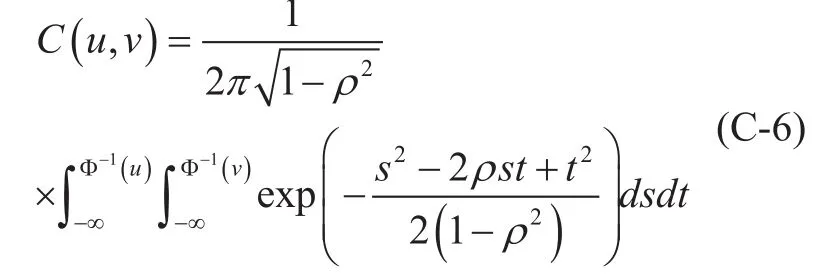
where Φ-1(·) is the inverse CDF of the standard Gaussian distribution.

Reference

[1] A. D. Panagopoulos, P.-D. M. Arapoglou and P.G. Cottis. “Satellite Communications At Ku Ka And V Bands:Propagation Impairments and Mitigation Techniques,” IEEE Communications Surveys, vol. 6, no. 03, 2004, pp. 2-14.

[2] R. Crane, Propagation Handbook for Wireless Communication System Design[M], Crc Press,2003

[3] R. Kaul, R. Wallace and G. Kinal, A propagation effects handbook for satellite systems design.A summary of propagation impairments on 10-100 GHz satellite links, with techniques for system design[M], National Aeronautics and Space Administration, Scientific and Technical Information Branch, 1981

[4] M. S. Alouini, S. A. Borgsmiller and P. G. Steあes.“Channel characterization and modeling for Kaband very small aperture terminals,” Proceedings of the IEEE, vol. 85, no. 6, 1997, pp. 981-997.

[5] ITU-R, Attenuation due to clouds and fog, Rec.P.840-5, Geneva, 2012

[6] W. Zhang, S. I. Karhu and E. T. Salonen. “Predictions of radiowave attenuations due to a melting layer of precipitation,” IEEE Transactions on Antennas and Propagation, vol. 42, no. 4, 1994,pp. 492-500.

[7] J. D. Kanellopoulos and R. H. Clarke. “A study of the joint statistics of rain depolarization and attenuation applied to the prediction of radio link performance,” Radio Science, vol. 16, no. 2,1981, pp. 203-211.

[8] T. Moulsley and E. Vilar. “Experimental and theoretical statistics of microwave amplitude scintillations on satellite down-links,” IEEE Transactions on Antennas and Propagation, vol. 30, no.6, 1982, pp. 1099-1106.

[9] ITU-R, Propagation data and prediction methods required for the design of earth-space telecommunication systems, Rec. P.618-9, Geneva,2008

[10] W. L. Stutzman. “The Special Section on Propagation Effects on Satellite Communication Links,” Proceedings of the IEEE, vol. 81, no. 6,1993, pp. 850-855.

[11] A. Afzal and S. A. Hassan. “Stochastic Modeling of Cooperative Multi-Hop Strip Networks With Fixed Hop Boundaries,” IEEE Transactions on Wireless Communications, vol. 13, no. 8, 2014,pp. 4146-4155.

[12] A. O. Kaya, L. J. Greenstein and W. Trappe.“Characterizing indoor wireless channels via ray tracing combined with stochastic modeling,”IEEE Transactions on Wireless Communications,vol. 8, no. 8, 2009, pp. 4165-4175.

[13] S. Priebe and T. Kurner. “Stochastic Modeling of THz Indoor Radio Channels,” IEEE Transactions on Wireless Communications, vol. 12, no. 9,2013, pp. 4445-4455.

[14] L. H. A fify, H. ElSawy, T. Y. Al-Naあouri and M. S.Alouini. “A Uni fied Stochastic Geometry Model for MIMO Cellular Networks With Retransmissions,” IEEE Transactions on Wireless Communications, vol. 15, no. 12, 2016, pp. 8595-8609.

[15] K. S. Ali, H. ElSawy and M. S. Alouini. “Modeling Cellular Networks With Full-Duplex D2D Communication: A Stochastic Geometry Approach,”IEEE Transactions on Communications, vol. 64,no. 10, 2016, pp. 4409-4424.

[16] T. Maseng and P. Bakken. “A Stochastic Dynamic Model of Rain Attenuation,” IEEE Transactions on Communications, vol. 29, no. 5, 1981, pp.660-669.

[17] R. M. Manning. “A unified statistical rain-attenuation model for communication link fade predictions and optimal stochastic fade control design using a location-dependent rain-statistics database,” International Journal of Satellite Communications, vol. 8, no. 1, 1990, pp. 11-30.

[18] M. J. Leitao and P. A. Watson. “Method for prediction of attenuation on earth-space links based on radar measurements of the physical structure of rainfall,” Communications, Radar and Signal Processing, IEE Proceedings F, vol.133, no. 4, 1986, pp. 429-440.

[19] S. H. Lin. “A method for calculating rain attenuation distributions on microwave paths,” The Bell System Technical Journal, vol. 54, no. 6,1975, pp. 1051-1086.

[20] K. Morita and I. Higuti. “Prediction methods for rain attenuation distributions of micro and millimeter waves,” REVIEW OF THE ELECTRICAL COMMUNICATIONS LABORATORIES, vol. 24, no.7-8, 1976, pp. 651-668.

[21] C. Capsoni, F. Fedi, C. Magistroni, A. Paraboni and A. Pawlina. “Data and theory for a new model of the horizontal structure of rain cells for propagation applications,” Radio Science,vol. 22, no. 3, 1987, pp. 395-404.

[22] R. Olsen, D. Rogers and D. Hodge. “The aRbrelation in the calculation of rain attenuation,” IEEE Transactions on Antennas and Propagation, vol.26, no. 2, 1978, pp. 318-329.

[23] J. O. Laws and D. A. Parsons. “The relation of raindrop-size to intensity,” Eos Transactions American Geophysical Union, vol. 24, no. 2,1943, pp. 248-262.

[24] J. S. Marshall and W. M. K. Palmer. “THE DISTRIBUTION OF RAINDROPS WITH SIZE,” Journal of the Atmospheric Sciences, vol. 5, no. 4, 1948, pp.165-166.

[25] J. Joss, J. Thams and A. Waldvogel, “The variation of rain drop-size distributions at Locarno,”Proc. International Conference on Cloud Physics,1968, pp. 1-1

[26] B. Oksendal, Stochastic Differential Equations[M], Springer, 2005

[27] A. Papoulis, Probability, Random Variables, and Stochastic Processes[M], McGraw-Hill, 1965

[28] S. H. Lin. “Statistical behavior of rain attenuation,” The Bell System Technical Journal, vol. 52,no. 4, 1973, pp. 557-581.

[29] S. H. Lin. “Mere on rain rate distributions and extreme value statistics,” The Bell System Technical Journal, vol. 57, no. 5, 1978, pp. 1545-1568.

[30] G. E. Uhlenbeck and L. S. Ornstein. “On the Theory of the Brownian Motion,” Physical Review,vol. 36, no. 5, 1930, pp. 823-841.

[31] F. Lacoste, M. Bousquet, L. Castanet, F. Cornet and J. Lemorton. “Improvement of the ONERACNES rain attenuation time series synthesizer and validation of the dynamic characteristics of the generated Fade events,” Space Communications, vol. 20, no. 1-2, 2005, pp. 45-59.

[32] ITU-R, “Tropospheric attenuation time series synthesis” Recommendation 1853, 2009

[33] S. O. Rice. “Distribution of the Duration of Fades in Radio Transmission: Gaussian Noise Model,”Bell Labs Technical Journal, vol. 37, no. 3, 1958,pp. 581–635.

[34] S. A. Kanellopoulos, A. D. Panagopoulos and J.D. Kanellopoulos. “Calculation of the Dynamic Input Parameter for a Stochastic Model Simulating Rain Attenuation: A Novel Mathematical Approach,” IEEE Transactions on Antennas and Propagation, vol. 55, no. 11, 2007, pp. 3257-3264.

[35] V. Y. Kontorovich and V. Z. Lyandres. “Stochastic diあerential equations: an approach to the generation of continuous non-Gaussian processes,”IEEE Transactions on Signal Processing, vol. 43,no. 10, 1995, pp. 2372-2385.

[36] F. J. A. Andrade and L. A. R. d. S. Mello. “Rain Attenuation Time Series Synthesizer Based on the Gamma Distribution,” IEEE Antennas and Wireless Propagation Letters, vol. 10, no. 2011,pp. 1381-1384.

[37] S. A. Kanellopoulos, A. D. Panagopoulos, C. I.Kourogiorgas and J. D. Kanellopoulos. “Satellite and Terrestrial Links Rain Attenuation Time Series Generator for Heavy Rain Climatic Regions,”IEEE Transactions on Antennas and Propagation,vol. 61, no. 6, 2013, pp. 3396-3399.

[38] X. Boulanger, L. Feral, L. Castanet, N. Jeannin,G. Carrie and F. Lacoste. “A Rain Attenuation Time-Series Synthesizer Based on a Dirac and Lognormal Distribution,” IEEE Transactions on Antennas and Propagation, vol. 61, no. 3, 2013,pp. 1396-1406.

[39] S. A. Kanellopoulos, C. I. Kourogiorgas, A.D. Panagopoulos, S. N. Livieratos and G. E.Chatzarakis. “Channel Model for Satellite Communication Links Above 10GHz Based on Weibull Distribution,” IEEE Communications Letters, vol. 18, no. 4, 2014, pp. 568-571.

[40] C. Kourogiorgas, A. D. Panagopoulos, S. N. Livieratos and G. E. Chatzarakis. “Rain attenuation time series synthesizer based on inverse Gauss-ian distribution,” Electronics Letters, vol. 51, no.25, 2015, pp. 2162-2164.

[41] T. Maruyama, Y. Shirato, M. Akimoto and M.Nakatsugawa. “Service Area Expansion of Quasi-Millimeter FWA Systems Through Site Diversity Based on Detailed Rainfall Intensity Data,”IEEE Transactions on Antennas and Propagation,vol. 56, no. 10, 2008, pp. 3285-3292.

[42] P. A. Brodtkorb, P. Johannesson, G. Lindgren, I.Rychlik, J. Ryden and E. Sjo, “WAFO - A Matlab toolbox for analysis of random waves and loads,” Proc. The Tenth International Offshore and Polar Engineering Conference, 2000, pp. 1-1

[43] S. Livieratos, V. Katsambas and J. Kanellopoulos.“A Global Method for the Prediction of the Slant Path Rain Attenuation Statistics,” Journal of Electromagnetic Waves & Applications, vol. 14, no.14, 2000, pp. 713-724.

[44] A. D. Panagopoulos, P. D. M. Arapoglou, J. D.Kanellopoulos and P. G. Cottis. “Long-term rain attenuation probability and site diversity gain prediction formulas,” IEEE Transactions on Antennas and Propagation, vol. 53, no. 7, 2005, pp.2307-2313.

[45] C. I. Kourogiorgas, A. D. Panagopoulos, I. D.Kanellopoulos and G. K. Karagiannidis, “On the Inverse Gaussian modeling of rainfall rate and slant path and terrestrial links rain attenuation,”Proc. European Conference on Antennas and Propagation, Eucap, 2012, pp. 1463-1467

[46] Andrade, F. J. A. Mello, Silva, L. A. R. D. Pontes,M. S. Rodrigues and E. C. Marcio. “Statistical modeling of rain attenuation in tropical terrestrial links,” Journal of Microwaves Optoelectronics & Electromagnetic Applications, vol. 11, no.2, 2012, pp. 296-303.

[47] C. Kourogiorgas and A. D. Panagopoulos. “New physical-mathematical model for predicting slant-path rain attenuation statistics based on inverse Gaussian distribution,” IET Microwaves,Antennas & Propagation, vol. 7, no. 12, 2013,pp. 970-975.

[48] C. I. Kourogiorgas, A. D. Panagopoulos and J. D.Kanellopoulos. “On the Earth-Space Site Diversity Modeling: A Novel Physical-Mathematical Outage Prediction Model,” IEEE Transactions on Antennas and Propagation, vol. 60, no. 9, 2012,pp. 4391-4397.

[49] G. A. Karagiannis, A. D. Panagopoulos and J. D.Kanellopoulos. “Multidimensional Rain Attenuation Stochastic Dynamic Modeling: Application to Earth-Space Diversity Systems,” IEEE Transactions on Antennas and Propagation, vol. 60, no.11, 2012, pp. 5400-5411.

[50] J. D. Kanellopoulos, A. D. Panagopoulos and S.N. Livieratos. “A comparison of copolar and cochannel satellite interference prediction models with experimental results at 11.6 and 20 GHz,”International Journal of Satellite Communications and Networking, vol. 18, no. 2, 2000, pp.107–120.

[51] A. D. Panagopoulos, S. N. Livieratos and J. D.Kanellopoulos. “Interference analysis applied to a double site diversity Earth-space system: Rain height effects and simple regression-derived formulas,” Radio Science, vol. 37, no. 6, 2002, pp.15-11–15-19.

[52] M. Luglio, R. Mancini, C. Riva, A. Paraboni and F. Barbaliscia. “Large-scale site diversity for satellite communication networks,” International Journal of Satellite Communications and Networking, vol. 20, no. 4, 2002, pp. 251–260.

[53] A. D. Panagopoulos and J. D. Kanellopoulos. “On the rain attenuation dynamics: spatial-temporal analysis of rainfall rate and fade duration statistics,” International Journal of Satellite Communications and Networking, vol. 21, no. 6, 2003, pp.595–611.

[54] C. Kourogiorgas and A. D. Panagopoulos. “A Rain-Attenuation Stochastic Dynamic Model for LEO Satellite Systems Above 10 GHz,” IEEE Transactions on Vehicular Technology, vol. 64,no. 2, 2015, pp. 829-834.

[55] R. B. Nelsen, An Introduction to Copulas(Springer Series in Statistics)[M], 2006

[56] S. N. Livieratos, C. I. Kourogiorgas, A. D. Panagopoulos and G. E. Chatzarakis. “On the Prediction of Joint Rain Attenuation Statistics in Earth-Space Diversity Systems Using Copulas,” IEEE Transactions on Antennas and Propagation, vol.62, no. 4, 2014, pp. 2250-2257.

[57] C. I. Kourogiorgas, A. D. Panagopoulos, S. N.Livieratos and G. E. Chatzarakis, “Time diversity prediction modeling using Copula functions for satellite communication systems operating above 10GHz,” Proc. General Assembly and Scienti fic Symposium (URSI GASS), 2014 XXXIth URSI, 2014, pp. 1-4

[58] ITU-R. Databank DBSG3 2010 [Online]. Available: http://www.itu.int/publ/R-SOFT-SG3/en

[59] C. Kourogiorgas, A. Kelmendi, A. D. Panagopoulos and A. Vilhar. “On Rain Attenuation Time Series Generation: A New Simple Copula-based Channel Model for Satellite Slant Paths,” IEEE Transactions on Antennas and Propagation, vol.64, no. 7, 2016, pp. 3206-3211.

[60] A. Kelmendi, G. Kandus, A, x, vigelj, A. Vilhar,A. Hrovat and E. Leitgeb, “Evaluation of the Gaussian copula prediction method for joint rain attenuation statistics in Earth-satellite site diversity systems,” Proc. 2016 International Conference on Broadband Communications for Next Generation Networks and Multimedia Applications (CoBCom), 2016, pp. 1-6

[61] T. F. Coleman and Y. Li. “On the convergence of interior-re flective Newton methods for nonlinear minimization subject to bounds,” Mathematical Programming, vol. 67, no. 1, 1994, pp.189-224.

[62] T. F. Coleman and Y. Li. “An Interior, Trust Region Approach for Nonlinear Minimization Subject to Bounds,” Siam Journal on Optimization, vol.6, no. 2, 2006, pp. 418-445.

[63] J. D. Kanellopoulos, T. D. Kritikos and A. D. Panagopoulos. “Adjacent Satellite Interference Effects on the Outage Performance of a Dual Polarized Triple Site Diversity Scheme,” IEEE Transactions on Antennas and Propagation, vol.55, no. 7, 2007, pp. 2043-2055.

[64] R. M. Barts and W. L. Stutzman. “Modeling and simulation of mobile satellite propagation,” IEEE Transactions on Antennas and Propagation, vol.40, no. 4, 1992, pp. 375-382.

[65] E. Matricciani. “Transformation of rain attenuation statistics from fixed to mobile satellite communication systems,” IEEE Transactions on Vehicular Technology, vol. 44, no. 3, 1995, pp.565-569.

[66] [Online], Available: http://mathworld.wolfram.com/