Coordinated Resource Allocation for Satellite-Terrestrial Coexistence Based on Radio Maps

Yanmin Wang＊, Zhou Lu

China Academy of Electronics and Information Technology, Beijing 100041, China

＊ The corresponding author, email: yanmin-226@163.com

I. INTRODUCTION

To meet the growing challenge of spectrum scarcity, various spectrum efficiency enhancement strategies are being promoted and putting into practice. Therein lies coexistence of satellite and terrestrial wireless communication systems in the same frequency band, which is considered to be a quite promising solution for unprecedented spectrum demands [1, 2]. Lots of satellite-terrestrial coexistence techniques have been proposed under the cognitive radio framework in literature, including cooperative spectrum sensing, beamforming, and adaptive resource allocation [3, 4, 5], etc. A seminal work can be found in reference [2], in which the practical limitation for spectrum sharing was precisely considered.

As an enabler for practical cognitive radio networks (CRNs), radio map (RM) is attracting more and more interests from academia and industry [6, 7, 8]. The essential functionality of an RM is to construct a comprehensive dynamic spectrum map for a CRN, by merging multi-domain information from geolocation databases and continuous spectrum measurements collected from sensors. To estimate the state of locations where there is no measurement data, different kinds of RM construction techniques have been presented [9, 10, 11],which can be classified into spatial statistics based methods [9] and transmitter location determination based methods [10]. However,how to efficiently utilize RM for enhancing spectrum efficiency are still open and yet to be explored [7][8].

Based on the largescale channel state information at the transmitter (CSIT),which is derived from the RM, we propose an optimized power allocation scheme to improve the achievable sum rate of the terrestrial system.

In this paper, we focus on a scenario where a satellite communication system and a terrestrial distributed antenna system (DAS) coexist via spectrum sharing, and propose a power allocation algorithm for the terrestrial system,as well as an opportunistic user scheduling scheme for the satellite system by utilizing RM. As an advantaged architecture for terrestrial wireless communication systems [12,13, 14], DAS has been widely adopted in 4G wireless networks and will continue to prop up 5G networks [15]. Specifically, the uplink of the satellite communication system acts as the incumbent link, and the downlink of the DAS tries to reuse the same frequency band as the cognitive link. To achieve a maximum system sum rate, power allocation is adopted in DAS to opportunistically transmit to users at less interfered locations, based on the interference distribution information derived from RM.Only the large-scale channel state information at the transmitter side (CSIT) is assumed in DAS, to ease practical implementations [15,16, 17] and match the long-term statistical characteristic of RM as well [7]. For the satellite side, an opportunistic user scheduling scheme is presented, to reduce the harmful interference to the terrestrial mobile users.Similar to the terrestrial case, the scheduling scheme also uses only the large-scale CSIT.

Fig. 1. Illustration of a spectral coexistence scenario of GEO mobile satellite communication uplink and terrestrial DAS downlink.

The rest of the paper is organized as follows. The system model is illustrated in Section II, and Section III presents the power allocation algorithm for the terrestrial system and the opportunistic user scheduling scheme for the satellite system based on RM. Simulation results are given in section IV, and Section V concludes the paper. Throughout the paper,lower case and upper case boldface symbols denote vectors and matrices, respectively. Inis an identity matrix with dimension n. (.)Hdenotes the transpose conjugate. ℂM×Nrepresents the complex matrix space composed of M×N matrices and CN denotes a complex Gaussian distribution. E(.)and tr(.) represent the expectation and the trace operator, respectively.

II. SYSTEM MODEL

2.1 Scenario description

As illustrated in figure 1, we consider a spectral coexistence scenario of GEO mobile satellite communication uplink and terrestrial DAS downlink, e.g., both in the S band [2]. The satellite uplink is incumbent, and the DAS downlink reuses the same frequency band in a cognitive way. Note that due to the antenna pattern characteristics and the transit power constraints of terrestrial systems, the interference from the DAS to the satellite system can be ignored [2]. Consequently, the DAS only needs to deliberately avoid the interference from satellite terminals (STs) to its own users,and efficiently utilize the transmission power to achieve a maximum system sum rate. For the satellite side, it may adjust user scheduling strategy, so as to reduce the interference to the terrestrial users.

Assume that L STs are located in the same area with the DAS, and there are N distributed antenna elements (DAEs) and K users in the DAS. To be general, the STs, the DAEs,and the users are all supposed to be geographically randomly deployed in the coverage area [2]. Without loss of generality, each user is equipped with M antenna elements, and N≥MK.

2.2 Sum rate expression

With the assumption that all transmitted signals for the N DAEs in the DAS are jointly processed in a centralized processor as shown in figure 1, the received signal yk∈ℂM×1at user k (k=1,2,...,K ) can be written as

where Hk∈ℂM×Nis the channel matrix from the N DAEs to user k, and xk∈ℂN×1is the transmitted signal of user k (k=1,2,...,K ),andrepresents the channel vector between ST j (j=1,2,...,L ) and user k, and zj∈ℂ is the transmitted signal of ST j, and nkdenotes the white Gaussian noise at user k with

Composed of both random small-scale fading and slowly-varying large-scale fading [14][16], Hkcan be expressed as

where Sk∈ℂM×Nrepresents the small-scale fading, and each entry follows the complex Gaussian distribution, and Lk∈ℂN×Nis a diagonal matrix, representing the large-scale channel fading. We have

and

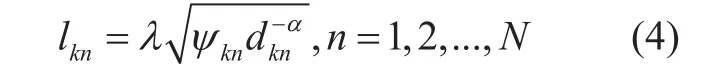
which indicates the total transmission loss between DAE n and user k. Particularly, λ is the amendment factor depending on concrete propagation environments, and ψknrepresents the shadow fading with lognormal distribution, and dknis the transmission distance, and α denotes the path-loss exponent. λ, ψknand α depend on application scenarios, and these parameters impact the system performance significantly. In general, for the case with larger transmission loss, the interference from STs to the terrestrial system will become more dominant. It can be analogized from (2)thatcan be decomposed as

As the RM is constructed via spectrum measurement, it can only indicate the large-scale CSIT with a construction cost limitation. Therefore, in the sequel,we assume only Lk(k=1,2,...,K ) and(j=1,2,...,L, k=1,2,...,K ) are available for the coordinated resource allocation optimization.

Suppose that the elements of xkare all independently complex Gaussian distributed and the transmit power of DAE n for user k is pkn, we can get that

For the satellite side, we assume the transmit power of ST j as

Taking expectation over the unknown smallscale CSITwe derive the interference covariance from all the STs to user k as

Similarly, taking expectation over the unknown small-scale CSIT Sk, we derive the interference covariance from all the other users to user k as

Correspondingly, de fine

and the average system sum rate of the DAS Rtcan be written as

In the following, we try to maximize Rtby coordinated resource allocation at both the terrestrial and the satellite sides.

III. COORDINATED RESOURCE ALLOCATION

In this section, we first optimize the power allocation strategy for the DAS system, so as to adapt to the diverse interference level at different users. Then, we present an opportunistic scheduling method for the satellite system, to control its harmful interference to the terrestrial users.

3.1 Power allocation for the terrestrial side

Under a transmission power constraint for each user, we can formulate the following optimization problem

Because of the expectation operator in the objective function, this optimization problem is dif ficult to solve. Moreover, the optimization variables exist in both the numerator and the denominator with the log function, which renders that the problem is non-convex [18].

In order to simplify the problem, we first approximate Rtas

with

Using the random matrix theory [16][19], we can derive (14) and (15).

Given Wk(k=1,2,...,K ), the problem in(13) can be recast as

Noting that the log function is monotonically increasing, we can equivalently have the following transformed problem

The problem in (17) is still challenging. However, we can transform it iteratively into a series of Geometric Programming (GP) problems [20].

By ι we denote the iterative step. Then,given the power allocation results for the ι−1 step,, we can de fine

Accordingly, we formulate the following optimization problem

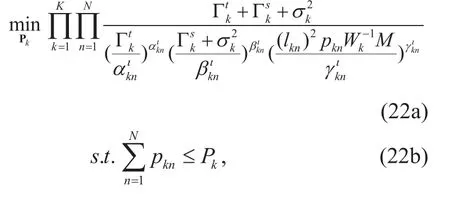
which fortunately is a standard GP problem.Consequently, we can solve it by using specialized tools. According to the inequality of arithmetic and geometric means and the fact that Rtis upper bounded, it is easy to prove that the iteration converges [13]. The details of the iterative algorithm is summarized in Algorithm 1.

3.2 Opportunistic scheduling for the satellite side

As shown in figure 2, for a given ST j, its interference to different terrestrial user is different. We can define the total leakage interference and the strongest leakage interference for ST j as follows

Then, the L online STs can be selected in an opportunistic fashion. Particularly, an order of all the waiting STs is first generated in the satellite gateway, according to the interference knowledge derived from the RM. The order can be obtained based on either the sum leakage interference as

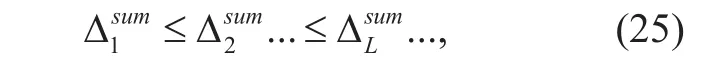
or the strongest leakage interference as

?

Fig. 2. Illustration of the inter-system interference. In this example, the leakage interference to user #1 (or #2) is the strongest one among those interference generated by ST #1 (or #2).

For both cases, STs 1～L will be scheduled. In a mobile communication scenario, the RM will dynamically change, and thereby the order of all the waiting STs should be adaptively updated. Thus, although only the L STs with the smallest leakage interference are scheduled, all the waiting STs can be served in an opportunistic fashion [21].

Moreover, the proposed scheduling method may largely reduce the leakage interference to the DAS users, hence the performance of the DAS can be improved.

Fig. 3. Illustration of the simulation setups.

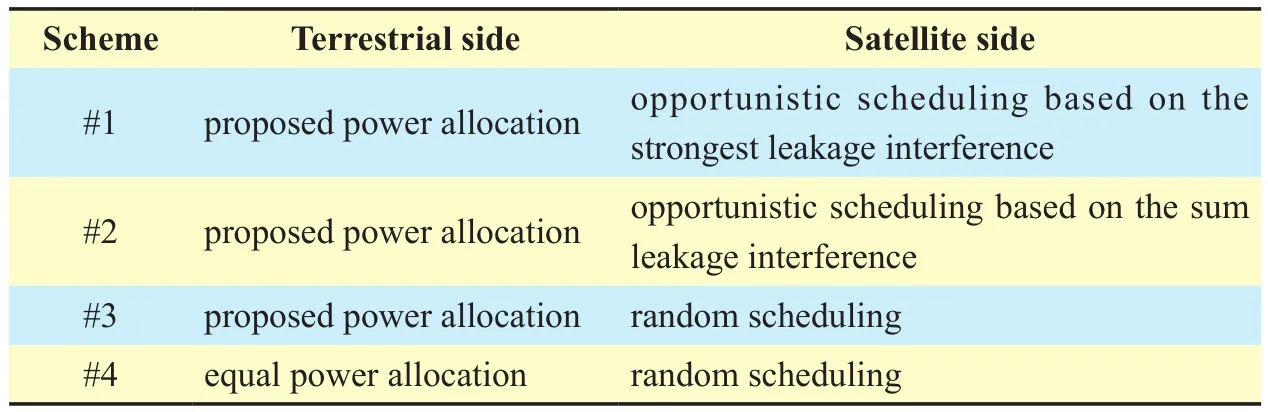
Table I. Resource allocation schemes considered in the simulation.

IV. SIMULATION RESULTS

In this section, we evaluate the performance of the proposed power allocation scheme and opportunistic scheduling scheme. As shown in figure 3, a circular coverage area is assumed.N=12 DAEs, and K=3 users with M=4 antenna elements each are deployed following uniform distribution within the inner circular area with a radius of r1=1000m . 5 STs are randomly deployed in the ring zone with 1000m≤r≤1200m. L=2 STs will be activated among these waiting STs.

The transmit power for each ST is assumed to be 30dBm, and the transmit power constraint for different users is supposed to be the same, which takes value from 20dBm to 40dBm. For the large-scale channel, the amendment factor is set as λ2= −30 (in dB),and the path-loss exponent is set as α=4, and the standard deviation of the shadow fading is set to be 8dB. The noise power is -107dBm.

We first compare the achievable sum rate of different resource allocation schemes. Four schemes have been taken into the comparison, as shown in table I. We can observe from figure 4 that the proposed power allocation scheme significantly outperforms the equal power allocation scheme. Because this scheme is designed according to only the large-scale CSIT (derived from the RM), it is hard to compare it with other existing schemes, which were designed based on full CSIT or imperfect CSIT with Gaussian errors. From the figure,we can also see that the proposed opportunistic scheduling scheme can provide a gain over traditional random scheduling, especially at the low signal to noise ratio (SNR) regime.The scheduling based on the strongest leakage interference performs a little better than that based on the sum leakage interference, which implies that the strongest leakage interference is the most dominant in fluence factor.

When the number of DAEs goes larger,we give simulation results for scheme #1 in figure 5, when the transmit power constraint equals to 30dBm. It can be seen that network densification [14] is effective for improving the performance of terrestrial systems, under the interference from satellite systems. On one hand, the average access distance can be reduced by deploying more DAEs. On the other hand, it also provides more spatial degree of freedom to utilize the transmit power more efficiently.

As for computational complexity, it is clear that the scheme #4 requires the least computational complexity. As the proposed opportunistic scheduling scheme only needs sorting the sum or the strongest leakage interference, it occupies negligible computational resources.The dominant computational complexity for schemes #1～#3 lies in the proposed power allocation scheme. In figure 6, the convergence performance of the proposed power allocation scheme is shown. 10 RMs (each RM corresponds to a random-generated system topology) are used in our simulations. We can find that for different RMs, 12 iterations are enough to converge for the proposed scheme.As the computational complexity of each iteration is quite low by adopting the mature tools for standard GP problem, the delay caused by the proposed power allocation scheme is quite short. This enables the practical implementation of the proposed scheme.

V. CONCLUSIONS

In this paper, we focus on the challenge of spectrum scarcity. A scenario where a satellite communication system and a terrestrial DAS coexist via spectrum sharing has been investigated. Particularly, we use the RM to derive the large-scale CSIT. For the terrestrial system, we have proposed an iterative power allocation scheme to adjust the transmit power of different DAEs, so as to adapt to the interference from the satellite system. For the satellite side, we have presented an opportunistic scheduling scheme, so as to carefully control the leakage interference. Simulation results have demonstrated that the proposed scheme outperforms traditional methods. Basically,the usage of RMs may greatly reduce the system overhead for channel estimation, thus it is quite promising for future dense hybrid satellite terrestrial networks.

Fig. 5. System performance with network densi fication.

Fig. 6. Convergence performance of the proposed power allocation scheme.

ACKNOWLEDGEMENT

This work was supported in part by the National Science Foundation of China under grant No. 61701457. The authors would like to sincerely thank the anonymous reviewers for their helpful comments.

[1] Maleki S, Chatzinotas S, Evans B, et al. Cognitive spectrum utilization in Ka band multibeam satellite communications[J]. IEEE Communications Magazine, 2015, 53(3): 24-29.

[2] Feng W, Ge N, Lu J. Coordinated satellite-ter-restrial networks: A robust spectrum sharing perspective[C]//Wireless and Optical Communication Conference (WOCC), 2017 26th. IEEE,2017: 1-5.

[3] Pierucci L, Fantacci R. MIMO cooperative spectrum sensing in hybrid satellite/terrestrial scenario[C]//Communication Workshop (ICCW),2015 IEEE International Conference on. IEEE,2015: 1617-1622.

[4] Sharma S K, Chatzinotas S, Grotz J, et al. 3D beamforming for spectral coexistence of satellite and terrestrial networks[C]//Vehicular Technology Conference (VTC Fall), 2015 IEEE 82nd.IEEE, 2015: 1-5.

[5] Lagunas E, Maleki S, Chatzinotas S, et al. Power and rate allocation in cognitive satellite uplink networks[C]//Communications (ICC), 2016 IEEE International Conference on. IEEE, 2016: 1-6.

[6] Akyildiz I F, Agusti R, Casadevall F, et al. Flexible and spectrum-aware radio access through measurements and modelling in cognitive radio systems[J]. FARAMIR Document: D2. 1,(ICT-248351), 2010.

[7] Yilmaz H B, Tugcu T, Alagoz F, et al. Radio environment map as enabler for practical cognitive radio networks[J]. IEEE Communications Magazine, 2013, 51(12): 162-169.

[8] Sharma S K, Bogale T E, Chatzinotas S, et al.Cognitive Radio Techniques Under Practical Imperfections: A Survey[J]. IEEE Communications Surveys and Tutorials, 2015, 17(4): 1858-1884.

[9] Riihijarvi J, Mahonen P, Sajjad S. Influence of transmitter configurations on spatial statistics of radio environment maps[C]//Personal, Indoor and Mobile Radio Communications, 2009 IEEE 20th International Symposium on. IEEE, 2009:853-857.

[10] Ureten S, Yongacoglu A, Petriu E. A comparison of interference cartography generation techniques in cognitive radio networks[C]//Communications (ICC), 2012 IEEE International Conference on. IEEE, 2012: 1879-1883.

[11] Yilmaz H B, Tugcu T. Location estimation-based radio environment map construction in fading channels[J]. Wireless communications and mobile computing, 2015, 15(3): 561-570.

[12] Feng W, Li Y, Gan J, et al. On the deployment of antenna elements in generalized multi-user distributed antenna systems[J]. Mobile Networks and Applications, 2011, 16(1): 35-45.

[13] Chen Y, Feng W, Zheng G. Optimum placement of UAV as relays[J]. IEEE Communications Letters, to appear, 2017.

[14] Feng W, Wang Y, Lin D, et al. When mmWave communications meet network densification:A scalable interference coordination perspective[J]. IEEE Journal on Selected Areas in Communications, 2017, 35(7): 1459-1471.

[15] Wei H, Feng W, Li Y, et al. Energy-efficient resource allocation for small-cell networks: a stable queue perspective[J]. China Communications, 2017, 14(10): 142-150.

[16] Feng W, Wang Y, Ge N, et al. Virtual MIMO in multi-cell distributed antenna systems: Coordinated transmissions with large-scale CSIT[J].IEEE Journal on Selected Areas in Communications, 2013, 31(10): 2067-2081.

[17] Chen Y, Feng W, Shi R, et al. Pilot-based channel estimation for AF relaying using energy harvesting[J]. IEEE Transactions on Vehicular Technology, 2017, 66(8): 6877-6886.

[18] Boyd S, Vandenberghe L. Convex optimization[M]. Cambridge university press, 2004.

[19] Zhang Y, Feng W, Ge N. Pilot power adaptation for tomographic channel estimation in distributed MIMO systems[J]. IET Communications,2017, 11(1): 112-118.

[20] Chiang M, Tan C W, Palomar D P, et al. Power control by geometric programming[J]. IEEE Transactions on Wireless Communications, 2007,6(7).

[21] Liu X, Chong E K P, Shroff N B. Opportunistic transmission scheduling with resource-sharing constraints in wireless networks[J]. IEEE Journal on Selected Areas in Communications, 2001,19(10): 2053-2064.