早期受扰混凝土受硫酸盐侵蚀后的受荷损伤模型

潘慧敏，王树伟，赵庆新

(燕山大学 建筑工程与力学学院，河北 秦皇岛　066004)

在桥梁结构材料中，混凝土材料占有很大比重，其质量直接影响着桥梁结构的安全[1]。混凝土在终凝前，水泥浆体逐渐硬化，但混凝土内部初始微结构并未完全形成，对外界扰动的影响会比较敏感[2-3]。因此，我国早年的施工规范曾这样规定：混凝土在初凝后终凝前的这一阶段不能受到任何扰动，否则扰动力会使未完全硬化的混凝土构件发生破坏[4]。铁路桥梁在新建、改造和修补的过程中，新浇筑混凝土受外部振动干扰的情况时有发生。比如，在对旧桥进行必要的养护、加固和翻新时，很多地区交通要道不具备封闭交通通行的条件，当火车通过频率很高时，新浇筑混凝土的凝结硬化过程可能会受到车桥振动的持续影响[5-6]。

针对列车振动对新浇筑混凝土性能的影响，国内外学者开展了相关探索性研究。Manning D G[7]研究了对破损混凝土桥面进行修补时，新浇筑混凝土受桥梁振动的影响。研究表明，当混凝土配合比设计合理时，桥梁振动对钢筋混凝土的黏结强度和抗压强度影响不大。卜良桃[8]以跨陇海铁路和京九铁路处的2座多跨拼接连续刚构桥为背景，通过现场测试和试验模拟的方法，对现浇混凝土受火车行驶振动的影响进行了研究。结果表明，当振幅控制在一定范围内时，振动对混凝土强度的影响并不显著。但当振幅较大时，必须采取隔振、减振措施。陈大华[5]研究了桥梁新浇筑混凝土受桥下列车振动的影响，结果表明，列车振动使混凝土强度下降5%左右。叶东升[9]通过现场测试，研究了火车行驶振动对新浇筑混凝土性能的影响。研究认为：火车振动干扰在一定程度上影响了混凝土内部结构的形成过程。Kwan[10]研究了对桥面进行加宽施工时车辆荷载振动对早龄期混凝土的影响，试验结果表明：当振动初始振幅超过3 mm时，混凝土会出现较大的裂缝，裂缝宽度超过了0.2 mm。蒋正武[11]研究了混凝土早期性能受车桥耦合振动的影响，认为扰动增加了混凝土内部的有害孔比例，使混凝土产生永久微裂纹，影响混凝土长期性能。综上，列车振动对新浇筑混凝土的影响在施工中是一个不容忽视的问题。已有研究表明[12-13]，列车振动引起的扰动会使基体中产生微裂缝，破坏界面过渡区的黏结强度，影响混凝土强度增长，降低其后期耐久性。

在影响混凝土耐久性的诸多因素中，硫酸盐对混凝土的侵蚀破坏是引起混凝土材料损伤破坏的重要因素[14]。目前，对于受扰混凝土在硫酸盐侵蚀环境中的性能研究相对较少，受扰受侵蚀混凝土服役时在荷载作用下的损伤评定及演化规律研究更是未见报道。混凝土材料在受应力作用时，产生的变形和损伤会释放应力波，产生声发射现象(Acoustic Emission，AE)，故声发射的孕育和产生也意味着材料内部损伤的形成和发展[15]，借助声发射可以推断混凝土内部结构的变化及损伤程度。

以列车振动对新浇筑混凝土的影响为研究背景，基于损伤力学基本理论，考虑扰动和侵蚀对混凝土造成的损伤，推导混凝土受压状态下的损伤演化方程和本构方程。通过对受硫酸盐侵蚀的早期受扰混凝土试件进行抗压试验，进行早期扰动对受侵蚀混凝土应力—应变关系影响研究以及声发射分析，建立早期受扰混凝土受硫酸盐侵蚀后的受荷损伤模型。

1　模型推导

1.1　声发射活性函数

材料产生声发射本身就意味着损伤，声发射活性是声发射特征中的重要参数。为了使混凝土材料的声发射活性能够定量表述，首先应建立声发射活性函数。纪洪广[16]、Ohtsu[17]的研究认为，不同应力水平下的声发射活性可以用声发射事件概率密度函数定量描述。

材料受荷载作用时，其相对应力水平从σ增加到σ+dσ的过程中必然会产生声发射现象，若声发射事件的概率密度函数为f(σ)， 则可以表示为[16]

(1)

式中：N为声发射事件数。

参考文献[18]，概率密度函数f(σ)可以用双曲线函数表示为

(2)

式中：a和b分别为与声发射速率和过程有关的参数。

将式(2)代入式(1)并积分，可得

N=cσaexp(bσ)

(3)

式中：c为积分常数。

积分常数c值受试验加载条件的影响，式(3)即为混凝土材料声发射的活性函数。

1.2　混凝土受荷损伤表征

材料的微结构和宏观物理性能发生变化时，其内部一定是发生了某种损伤。文献[19]从混凝土材料所产生声发射的机理出发，认为混凝土材料的损伤可以用声发射事件数表征，即

Dt=kN

(4)

式中：Dt为材料的损伤度；k为与试验条件有关的参数。

由式(4)可知，混凝土材料的损伤程度与声发射事件数成正比。将式(3)代入式(4)，可得

Dt=kcσaexp(bσ)

(5)

1.3　受扰受侵蚀混凝土损伤度及本构方程

材料的损伤及劣化规律可以用损伤度描述，材料损伤的力学行为可以由损伤度及本构方程体现。对于经受硫酸盐侵蚀作用的早期受扰混凝土而言，在承受压力荷载时，其损伤应包括两部分：压力荷载作用引起的宏观力学损伤和在硫酸盐侵蚀作用下的自身微观结构损伤。本文应用推广后的应变等价原理[20]，将早期受扰混凝土侵蚀后的损伤状态作为初始损伤，其损伤度为Ds，侵蚀后受压引起的损伤状态作为后期损伤状态，损伤度为Dt。则混凝土材料初始和后期损伤状态的本构关系分别为

σs=E0(1-Ds)εs

(6)

σ=Es(1-Dt)ε

(7)

式中：σs和σ分别为初始损伤状态和后期损伤状态的应力；εs和ε分别为初始损伤状态和后期损伤状态的应变；E0和Es分别为混凝土基准弹性模量、受扰受侵蚀后弹性模量。

根据损伤力学原理，可将Es表示为

Es=E0(1-Ds)

(8)

将式(8)代入式(7)，可得

σ=E0(1-Ds)(1-Dt)ε=E0(1-D)ε

(9)

其中，

D=Ds+Dt-DsDt

(10)

式中：D为受扰受侵蚀和受压力荷载引起的总损伤度。

将式(5)代入式(10)，得

D=Ds+kcσaexp(bσ)-Dskcσaexp(bσ)

(11)

将式(11)代入式(9)，得

σ=E0[1-Ds-kcσaexp(bσ)+

Dskcσaexp(bσ)]ε

(12)

式(11)和式(12)分别为受扰受侵蚀混凝土在压力荷载作用下的总损伤演化方程和本构模型。

2　试　验

2.1　试件制备

试件尺寸为边长100 mm的立方体，混凝土强度等级为C40，配合比为水泥∶水∶砂石∶石子=1∶0.43∶1.71∶2.57。试验用水泥为P·O 42.5R 普通硅酸盐水泥，粗集料为5～25 mm连续级配的破碎石灰岩，细集料选用细度模数为2.9的天然河砂，减水剂为聚羧酸高效减水剂，拌合水为自来水。在立方体试件非承压4个面对应布置传感器。

2.2　试验方法

扰动试验按照文献[21]的方法进行，由苏试DC-1000-15水平电动振动台提供扰动。参照文献[5—7]对列车振动频率的分析，确定振动频率为15 Hz，振幅4 mm，扰动形式为正弦振动。使混凝土在初凝至终凝时间段受扰动，扰动时间为40 min。设置5种受扰龄期，开始扰动所对应的混凝土贯入阻力区段分别为3.5～6.9，6.9～10.7，10.7～14.8，14.8～19.6，19.6～30.9 MPa。试件受扰结束后，置入标准养护室养护至28 d龄期进行硫酸盐侵蚀试验。

硫酸盐侵蚀试验按照GB/T 50082—2009《普通混凝土长期性能和耐久性能试验方法标准》实施，硫酸钠溶液浓度为7%(质量分数)。侵蚀到300 d龄期时，将干燥后的混凝土试件取出，测试各组试件的超声波波速，之后进行加载试验，加载过程中进行声发射采集。加载装置采用GAW-2000微机控制电液伺服压力试验机，声发射检测系统采用DS2系列全信息声发射信号分析仪。信号采样频率3 MHz，前置放大器增益为40 dB，噪音门槛值为45 db。

2.3　试验结果及分析

2.3.1应力—应变关系

图1给出了在单轴压力荷载作用下，不同受扰条件混凝土受硫酸盐侵蚀300 d后的应力—应变曲线。由于试验条件所限，本文只得到了应力应变曲线的上升段，故此处只对曲线上的2个特征值(峰值应力σc和弹性模量Ee)进行比较与分析。混凝土弹性模量取实测应力—应变曲线上σ=0.4σc与其应变ε的比值，即割线模量。由图1可以看出，受侵蚀混凝土的应力峰值较未侵蚀混凝土明显下移，说明硫酸盐侵蚀降低了混凝土的抗压强度。而在同样的受侵蚀程度下，早期受扰混凝土的峰值应力较未受扰混凝土有不同程度的损失。

图2给出了受扰受侵蚀混凝土的峰值应力和弹性模量相对未受扰混凝土的降低率与受扰龄期的关系。由图2可以看出：中期的扰动(10.7～14.8 MPa)对混凝土峰值应力和弹性模量的影响最大，相比未受扰动的受侵蚀混凝土，其峰值应力降低了36.1%，弹性模量降低了34.5%；临近终凝的扰动使峰值应力降低了14.3%，而临近初凝的扰动对峰值应力和弹性模量的影响均很小，尤其是弹性模量的降低率在1%以下，扰动影响基本可以忽略；在同样的受扰条件下，受侵蚀混凝土弹性模量的变化幅度较峰值应力的变化幅度略小。

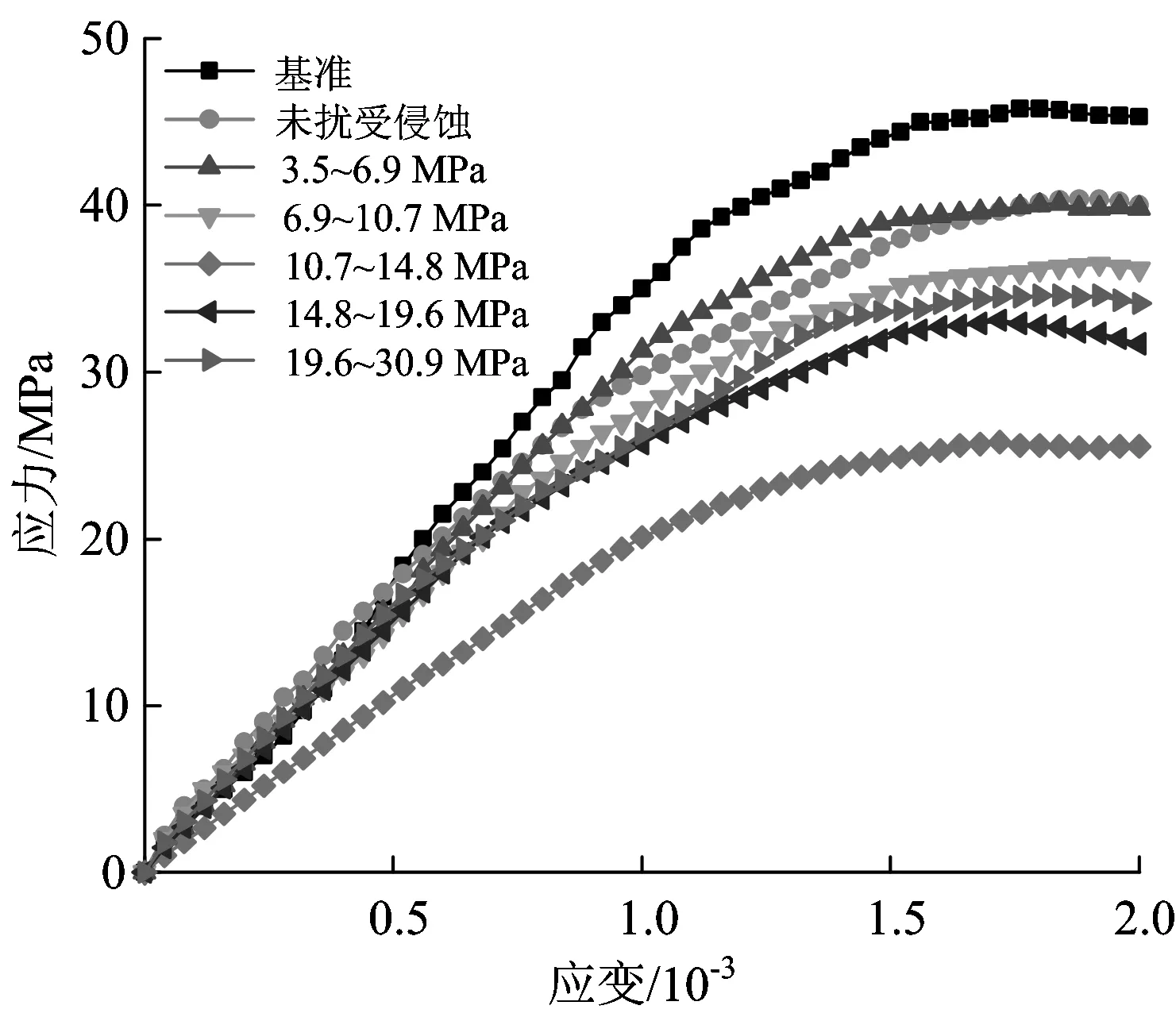
图1　不同受扰龄期的混凝土受压应力—应变曲线

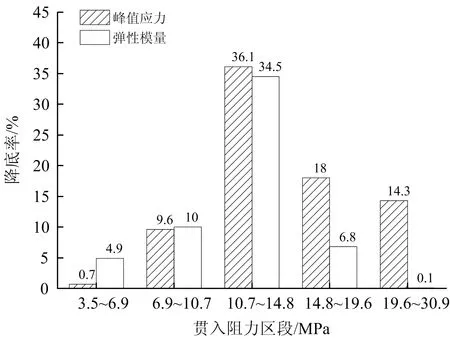
图2　受扰龄期对受侵蚀混凝土力学性能的影响

2.3.2声发射振铃计数

声发射振铃计数率是单位时间内振铃脉冲越过系统门槛的次数，其强弱与其变形和裂隙扩展密切相关，声发射振铃计数可以反映混凝土不同阶段的声发射基本参数特征。图3为受扰受侵蚀混凝土试件加载时的声发射振铃计数与相对应力水平关系曲线。

由图3可以看出，基准混凝土在加载的过程间隔出现多个声发射活跃区间。这是由于此试件内部结构致密，缺陷较少，在能量得到一次释放后，声发射事件骤降，应力得到重新分配。随着荷载的增大，试件中的能量再次释放，声发射事件又开始活跃，经过多次的能量释放和应力重新平衡，最后达到整体破坏。相比基准试件和未受扰试件，受扰试件在加载初期的密实阶段声发射事件数较少，主要原因是扰动使混凝土内已经存在有孔隙、裂隙等原始缺陷，经过硫酸盐侵蚀后缺陷增多，软化显著，加载过程中试件内部应力重新分配平衡的能力降低，以至于压密时变形破坏激烈程度比未受侵蚀的试样相对减弱，声发射活动因此而减弱[22]。荷载继续增加时，试件内部微裂纹扩展、积聚并联结成网，声发射事件数量开始增大。加载后期内部裂纹进一步扩展并贯通，声发射事件数量急剧上升。

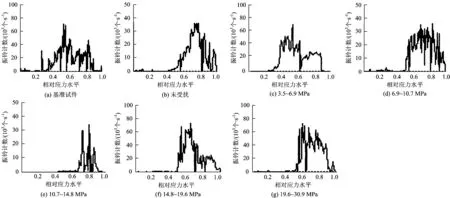
图3　混凝土声发射振铃计数与相对应力水平的关系

由图3还可以看出，中期受扰(10.7～14.8 MPa)的试件在整个加载过程中，声发射事件活跃区间最为集中，在相对应力水平达到0.5之前几乎没有声发射信号发生。这说明此阶段的扰动对混凝土影响最大，经过硫酸盐侵蚀作用，内部损伤更严重，损伤降低减小了晶体颗粒间的黏结力，使得试件在破裂时所需能量减少，产生明显声发射的时间也因此滞后。对试验加载过程中各试件的变形情况进行观察，从破坏时产生的声响可以得知，基准试件破坏时的声响比硬化中期和后期受扰的混凝土试件的破坏要大，说明受扰试件在破坏时刻所释放的能量较基准混凝土小。混凝土受压的声发射现象也佐证了作者之前[21]的研究结果。

3　模型建立

3.1　声发射活性函数参数拟合

试验采用声发射累积振铃计数表征声发射事件累积计数，则声发射活性函数可以表示为声发射累积振铃计数与对应试件极限荷载的比值[16]。

对本文7种类型试件的声发射事件试验数据根据式(3)进行统计回归处理，求得式(3)中对应各参数值，见表1。混凝土受压过程声发射事件数与相对应力的关系、拟合曲线，如图4所示。

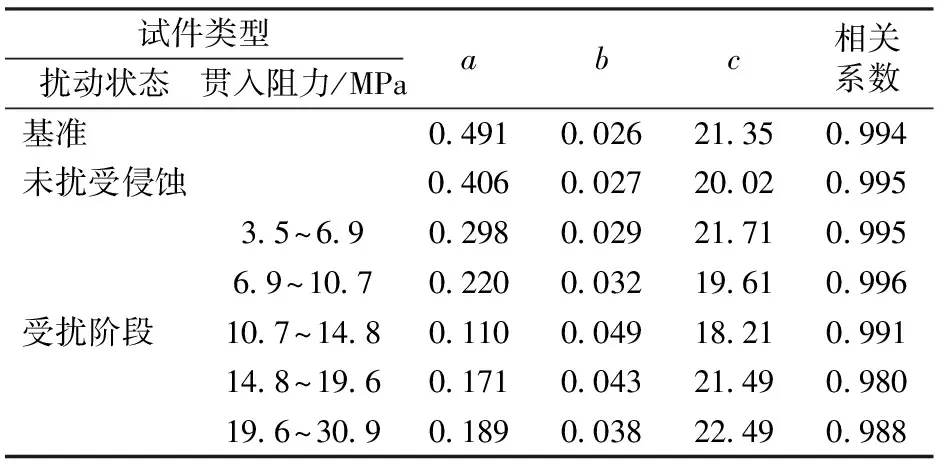
表1　活性函数参数拟合结果

由图4可以看出：以累积振铃计数表征声发射事件数，拟合出的声发射活性函数曲线与以累积振铃计数表示的声发射事件数试验曲线吻合良好，它们的相关系数分别为0.994，0.995，0.995，0.996，0.991，0.980和0.988；相比基准试件，受扰混凝土的声发射活性函数曲线早期更为平缓，相对应力水平超过50%后，声发射事件数骤然上升，曲线变陡。

由表1可以看出，中期受扰的混凝土b值最大，基准混凝土b值最小。因此与声发射过程有关的参数b值可以反映声发射早期和后期的活跃程度对比，早期声发射较少而后期声发射增多时，b值增大。

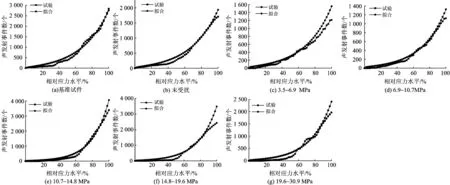
图4　声发射事件数拟合结果

3.2　受扰受侵蚀混凝土受压本构模型和损伤演化方程

声发射是混凝土微观结构变化的反应，也是混凝土应力阶段的函数。因此，由式(11)、式(12)可知只需求得参数k，即可得到混凝土损伤演化方程和本构方程。本试验混凝土试件的受侵蚀龄期为300 d，故侵蚀后的损伤变量Ds值为定值。Ds值根据试验中受侵蚀前后试件的超声波波速求得[23]，7种类型试件的Ds值分别为：0，0.15，0.20，0.23，0.50，0.29和0.25。本试验认为基准混凝土试件(未受扰且未受侵蚀时)的弹性模量相同，将表1中的a，b，c值代入式(12)，对图1中测得的应力应变值进行最小二乘法拟合，得到各组试件的E0，k值，见表2。

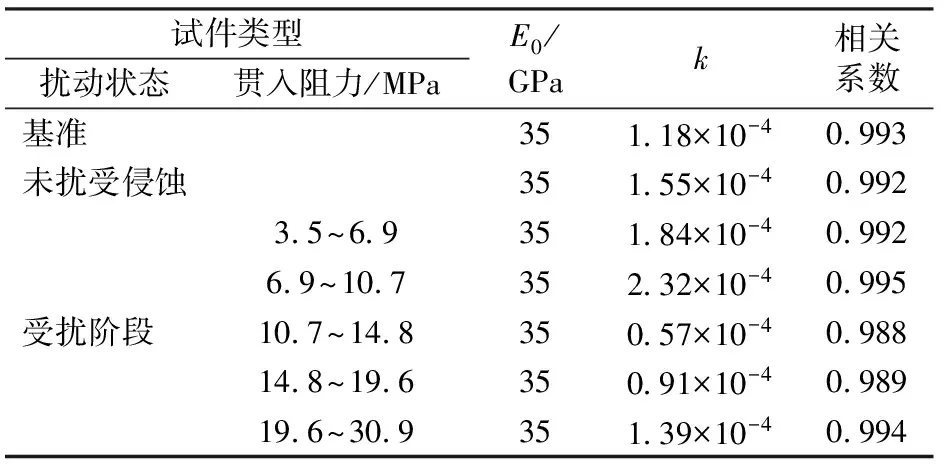
表2　本构模型参数拟合结果

图5给出了受扰受侵蚀混凝土受压本构关系及其拟合曲线。由图5可以看出：以声发射事件数表征混凝土的损伤程度，拟合计算出的应力—应变曲线与试验得出的应力—应变曲线吻合较好，相关系数分别为0.993，0.992，0.992，0.996，0.988，0.989和0.994。

将k值代入式(11)，即可得到不同受扰条件混凝土受侵蚀后在压力荷载作用下的总损伤度D发展情况，如图6所示。

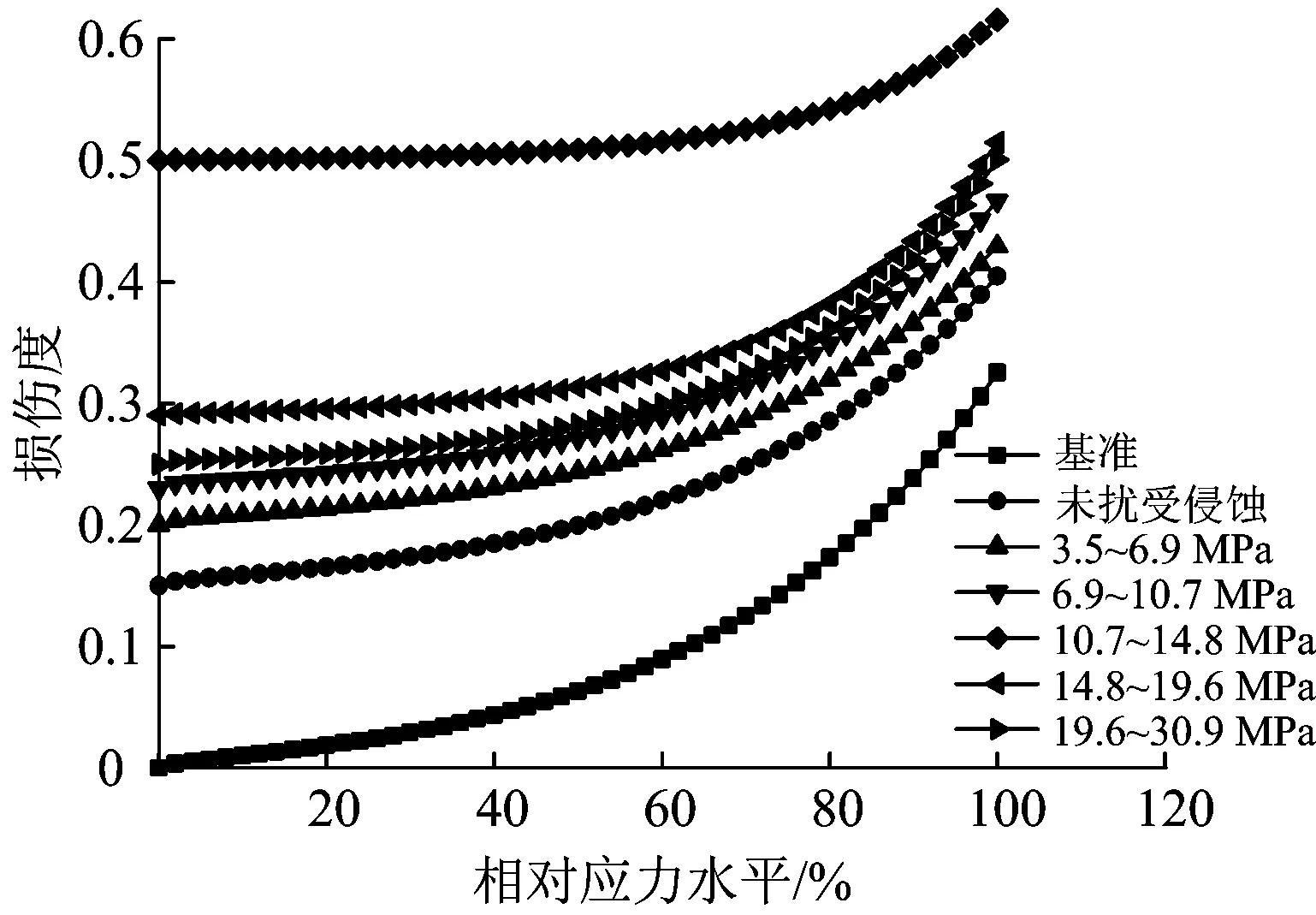
图6　混凝土总损伤度

由图6可以看出，受扰和未受扰混凝土在压力荷载作用下的损伤劣化程度都随着相对应力水平的增加而增大。受侵蚀混凝土受压损伤演化过程大致可以分为3个阶段：第1阶段，在受荷初期，试件处于压密和弹性阶段，总损伤度趋近于仅是侵蚀引起的损伤Ds；第2阶段，试件进入塑性变形阶段，随着压力荷载的增大，混凝土内部开始有新的微裂隙或微孔隙产生并扩展；第3阶段，混凝土内的微裂纹、微孔隙不断发展演化，裂缝体系开始变得不稳定，混凝土局部承载能力下降，损伤度急剧上升直至等于损伤临界值，材料产生破坏。

比较图6中不同受扰条件的曲线趋势可以看出，在同样的应力水平下，受扰混凝土的总损伤度比未受扰混凝土的大，说明扰动对混凝土造成的损伤对混凝土受荷作用下的损伤劣化影响较大。而且扰动造成的损伤越大，混凝土受荷初期压密阶段越长。以中期受扰的混凝土试件为例，在相对应力达到70%之前，混凝土几乎都处于初始压密阶段。这是由于中期受扰的混凝土在受压力荷载作用前，由扰动力和侵蚀引起的初始损伤就已达到0.5，内部已经存在较多的孔隙、微裂纹等初始缺陷，加速了混凝土的损伤劣化。

4　结　论

(1)凝结硬化期间的扰动使受扰混凝土应力—应变曲线上的峰值应力和弹性模量较未受扰混凝土有不同程度的降低。中期受扰的混凝土降低幅度最大，使峰值应力、弹性模量分别降低了36.1%和34.5%。临近初凝和终凝的扰动对峰值应力和弹性模量的影响较小。

(2)推导出的声发射活性函数曲线与声发射事件数试验曲线吻合良好，相关系数分别为0.994，0.995，0.995，0.996，0.991，0.980和0.988。相比基准试件，受扰混凝土的声发射活性函数曲线早期更为平缓，相对应力水平超过50%后，声发射事件数骤然上升，曲线变陡。

(3)基于损伤力学理论，以声发射事件数表征混凝土的损伤程度，得到的混凝土受压本构关系与试验结果吻合较好，相关系数分别为0.993，0.992，0.992，0.996，0.988，0.989和0.994。与未受扰混凝土相比，受扰侵蚀混凝土受荷初期压密阶段更长，后期损伤变量急剧上升。凝结硬化中期受扰的混凝土试件在相对应力达到70%之前，混凝土几乎都处于初始压密阶段。

[1]潘慧敏, 潘会滨, 赵庆新. 车桥振动对新浇筑混凝土性能的影响研究进展[J]. 硅酸盐通报, 2016, 35(2):449-452，457.

(PAN Huimin, PAN Huibin, ZHAO Qingxin. Development on Influence of Vehicle Bridge Vibration on the Performance of Young Concrete[J]. Bulletin of the Chinese Ceramic Society, 2016, 35(2):449-452，457. in Chinese)

[2]ABOLPOUR B, AFSAHI M M, HOSSEINI S G. Statistical Analysis of the Effective Factors on the 28 Days Compressive Strength and Setting Time of the Concrete[J]. Journal of Advanced Research, 2015, 6(5):699-709.

[3]潘慧敏, 赵庆新, 付军. 早龄期混凝土受扰性能研究进展[J]. 硅酸盐通报, 2017, 36(1):64-70.

(PAN Huimin, ZHAO Qingxin, FU Jun. Development on Performance of Early Age Concrete under Disturbance [J]. Bulletin of the Chinese Ceramic Society, 2017, 36(1):64-70. in Chinese)

[4]张大英. 重复振动对混凝土强度的影响[J]. 混凝土, 1992(2):14-17.

(ZHANG Daying. Effect of Repeated Vibration on Strength of Concrete[J]. Concrete, 1992(2):14-17. in Chinese)

[5]陈大华, 郭玉海, 李德恩, 等. 灌筑期间桥下列车振动对桥梁混凝土影响的试验研究[J]. 桥梁建设, 2003(6):22-24.

(CHEN Dahua, GUO Yuhai, LI Deen,et al. Test Study of Influences of Train Vibration under Bridge upon Bridge Concrete Being Cast[J]. Bridge Construction, 2003(6):22-24. in Chinese)

[6]ANSELL A, SILFWERBRAND J. The Vibration Resistance of Young and Early-Age Concrete[J]. Structural Concrete, 2003, 4(3):125-134.

[7]MANNING D G. Effects of Traffic-Induced Vibrations on Bridge-Deck Repairs[R]. Washington DC, USA: Transportation Research Board, National Academy of Sciences, 1981.

[8]卜良桃. 跨铁路线连续刚构桥现浇混凝土湿接头受火车行驶振动影响研究[D]. 长沙: 湖南大学, 2001.

(BU Liangtao. The Research on Influence of the Post-Casting Section of Continuous Rigid Bridge Suffered Vibration of Train[D]. Changsha:Hunan University, 2001. in Chinese)

[9]叶东升, 尚守平, 范跃武, 等. 跨铁路桥施工受火车振动影响的研究[J]. 公路, 2001(9):20-24.

(YE Dongsheng, SHANG Shouping, FAN Yuewu,et al. Research on Construction of Continuous Beam Bridge over Railway under Influence of Vibration Caused by Running Train[J]. Highway, 2001(9):20-24. in Chinese)

[10]KWAN A K H, NG P L. Effects of Traffic Vibration on Curing Concrete Stitch: Part Ⅰ—Test Method and Control Program[J]. Engineering Structures, 2007, 29(11):2871-2880.

[11]蒋正武, 任强, 袁政成. 车桥耦合振动对混凝土早期性能的影响及其损伤机理[J]. 建筑材料学报, 2015, 18(3):471-476.

(JIANG Zhengwu, REN Qiang, YUAN Zhengcheng. Effects of Vehicle-Bridge Coupled Vibration on Early-Age Properties of Concrete and Its Damage Mechanism[J]. Journal of Building Materials, 2015, 18(3):471-476. in Chinese)

[12]王世鸣, 李夕兵, 宫凤强, 等. 静载和动载下不同龄期混凝土力学特性的试验研究[J]. 工程力学, 2013,30(2):143-149.

(WANG Shiming, LI Xibing, GONG Fengqiang, et al. Experimental Study on Mechanical Properties of Different Ages Concrete under Static and Dynamic Load[J]. Engineering Mechanics, 2013, 30(2):143-149. in Chinese)

[13]DUNHAM M R, RUSH A S, HANSON J H. Effects of Induced Vibrations on Early Age Concrete[J]. Journal of Performance of Constructed Facilities, 2007, 21(3):179-184.

[14]GAO J, YU Z, SONG L, et al. Durability of Concrete Exposed to Sulfate Attack under Flexural Loading and Drying-Wetting Cycles[J]. Construction & Building Materials, 2013, 39(2):33-38.

[15]赖于树, 熊燕, 程龙飞. 混凝土受载试验全过程声发射特性研究与应用[J]. 建筑材料学报, 2015, 18(3):380-386.

(LAI Yushu, XIONG Yan, CHENG Longfeng. Study of Characteristics of Acoustic Emission during Entire Loading Tests of Concrete and Its Application[J]. Journal of Building Materials, 2015, 18(3):380-386. in Chinese)

[16]纪洪广, 蔡美峰. 混凝土材料声发射与应力—应变参量耦合关系及应用[J]. 岩石力学与工程学报, 2003,22(2): 227-231.

(JI Hongguang, CAI Meifeng. Coupling Constitutive Relation between AE Parameter and Stress-Strain and Its Application[J]. Chinese Journal of Rock Mechanics and Engineering, 2003,22(2):227-231. in Chinese)

[17]OHTSU M. Rate Process Analysis of Acoustic Emission Activity in Core Test of Concrete[J]. Proceedings of the Japan Society of Civil Engineers, 2010(442):211-217.

[18]KARCILI M, ALVER N, OHTSU M. Application of AE Rate-Process Analysis to Damaged Concrete Structures Due to Earthquake[J]. Materials and Structures, 2016, 49(6):2171-2178.

[19]纪洪广, 张天森, 蔡美峰, 等. 混凝土材料损伤的声发射动态监测试验研究[J]. 岩石力学与工程学报, 2000, 19(2): 165-168.

(JI Hongguang, ZHANG Tiansen, CAI Meifeng,et al. Experimental Study on Concrete Damage by Dynamic Measurement of Acoustic Emission[J]. Chinese Journal of Rock Mechanics and Engineering, 2000, 19(2):165-168. in Chinese)

[20]张全胜, 杨更社, 任建喜. 岩石损伤变量及本构方程的新探讨[J].岩石力学与工程学报, 2003, 22(1):30-34.

(ZHANG Quansheng, YANG Gengshe, REN Jianxi. New Study of Damage Variable and Constitutive Equation of Rock[J]. Chinese Journal of Rock Mechanics and Engineering, 2003, 22(1):30-34. in Chinese)

[21]潘慧敏, 王奉献, 赵庆新. 硬化期扰动对混凝土力学性能的影响[J]. 建筑材料学报, 2016, 19(4):631-636.

(PAN Huimin, WANG Fengxian, ZHAO Qingxin. Influence of Disturbance in Hardening Stage on Mechanical Properties of Concrete[J]. Journal of Building Materials, 2016, 19(4):631-636. in Chinese)

[22]刘娟红, 赵力, 宋少民, 等. 混凝土硫酸盐腐蚀损伤的声波与声发射变化特征及机理[J]. 工程科学学报, 2016, 38(8):1075-1081.

(LIU Juanhong, ZHAO Li, SONG Shaomin, et al. Ultrasonic Velocity and Acoustic Emission Properties of Concrete Eroded by Sulfate and Its Damage Mechanism[J]. Chinese Journal of Engineering, 2016, 38(8):1075-1081. in Chinese)

[23]CHEN J, SONG H, ZHANG M, et al. Theoretical Analysis on the Nucleation of Micro-Damage in Cement Mortar under Compressive Loading and Sulfate Attack[J]. Acta Mechanica Solida Sinica, 2013, 26(1):53-61.