顺层岩体各向异性对隧道地震响应的影响

胡鸿运，周晓军，汪精河

(1.西南交通大学 土木工程学院，四川 成都　610031；2.西南交通大学 交通隧道工程教育部重点实验室，四川 成都　610031；3.兰州交通大学 甘肃省道路桥梁与地下工程重点实验室，甘肃 兰州　730070)

大量隧道震害表明，隧道穿越地层的地质条件、岩层结构等对隧道结构的地震响应影响极大[1-2]，例如在5.12汶川8.0级地震震害调查中发现，围岩软硬互层的隧道破坏较硬岩隧道严重[3]。顺层岩体隧道(即岩层走向与隧道轴线平行、岩层倾向与隧道轴线垂直的情形)是典型的层状岩体隧道，与均质岩体隧道相比，顺层岩体隧道地震响应的主要特征之一是衬砌结构承受显著不对称的地震荷载，衬砌内力也显著不对称或非反对称(非反对称是指左右对称位置内力的数值不等、方向相反)[4]，这是由顺层岩体的横观各向同性而产生的。但近年国内外相关研究通常将隧道围岩假定为各向同性介质[5-15]，这无法反映上述不对称性或非反对称性，因此，应对顺层岩体隧道地震响应的规律进行研究。

为此，本文基于顺层岩体横观各向同性的弹性本构关系(因在极短期的迅速变化的动力作用下，岩体主要表现为弹性[16])，应用黏弹性边界的时域波动理论，提出顺层岩体中二维平面地震波从隧道底部入射时的输入方法。以某顺层岩体高速铁路隧道为工程背景，采用ANSYS软件进行地震时隧道动力响应的数值模拟分析，研究qP波和qSV波入射时岩层各向异性强度对隧道地震响应不对称性或非反对称性的影响。

1　材料参数及计算模型

1.1　衬砌参数

本文以某典型开挖断面的高速铁路深埋隧道为研究对象，如图1所示，隧道开挖最大宽度为15 m。

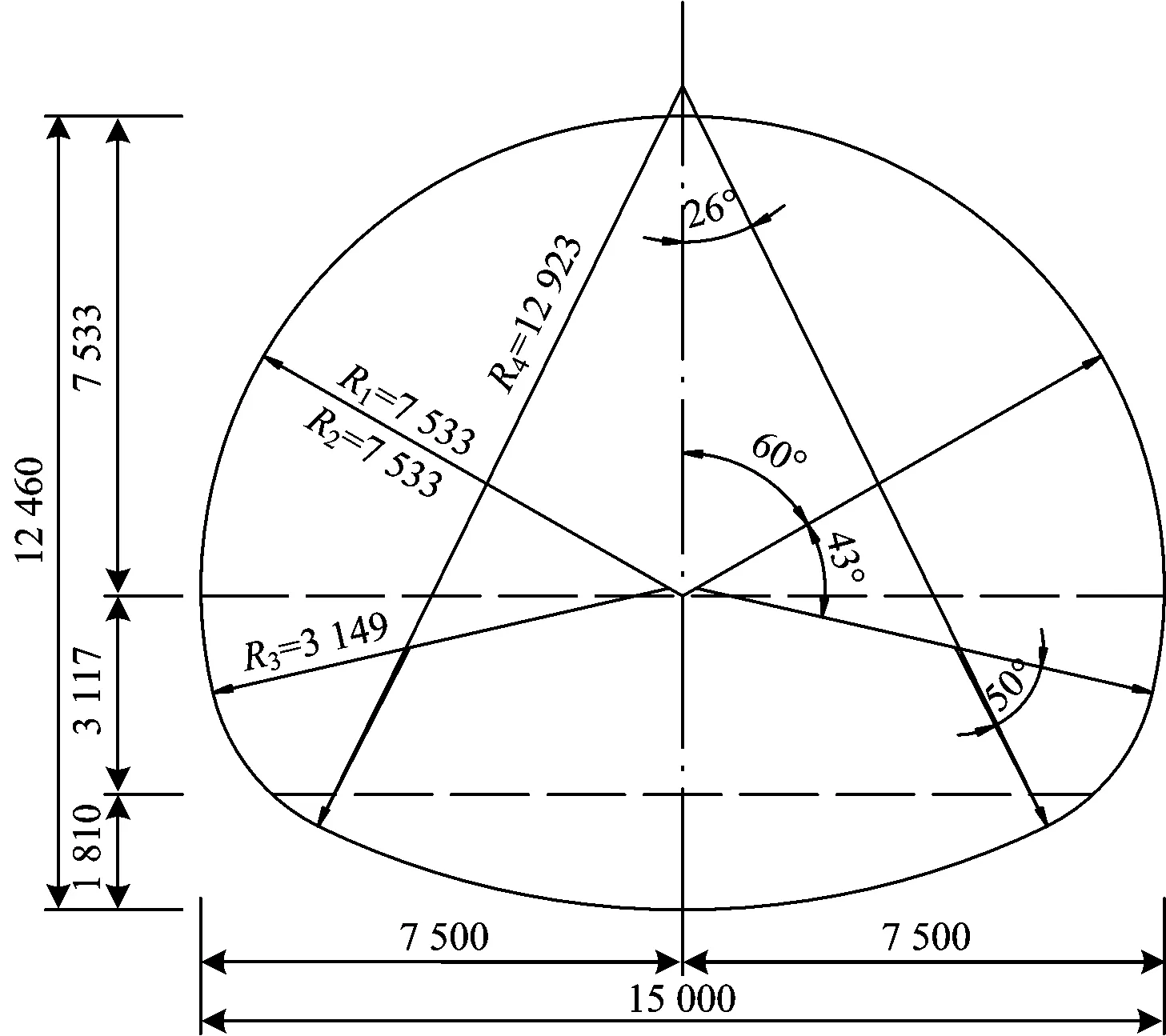
图1　隧道开挖断面(单位：mm)

隧道二次衬砌：厚度为600 mm，C35混凝土，配筋率为0.35%，弹性模量为31.5 GPa，泊松比为0.2，重度为25 kN·m-3。为更清晰地观察顺层岩体隧道地震响应的特征，略去加固层和初期支护。

1.2　顺层岩体参数

为便于对比分析，根据顺层岩体各向异性强度依次增强的规则，即岩体Thomsen参数[17]中表征横观各向同性介质各向异性强度的3个无量纲因子ε，γ和δ(以及ε-δ)的单调性一致[18]且增幅均匀的规则，设定有5组顺层岩体，分别标记为D1， D2，…，D5，其参数详见表1。

表1　地层参数表

1.3　计算模型

采用ANSYS软件建立平面有限元模型，以隧道中心为中心截取1 000 m×1 000 m的正方形区域进行离散，顺层岩体采用plane42单元、衬砌采用beam3单元、黏弹性边界采用combin14单元模拟。积分步长为0.01 s。黏弹性边界弹簧—阻尼参数的计算详见文献[4]，其中法向修正系数αN与切向修正系数αT分别取1.0和0.5[19]。

地震波的总波场仅考虑入射波场和隧道反射波场，并采用在有限计算区域4个边界面上设置近似黏弹性边界的方法模拟，其中，隧道反射波被黏弹性边界自然吸收。因为，根据地震波动理论可知，地震波传播到地面时会产生反射，所以地震波的总波场为自由波场(即入射波场)和散射波场(即地面反射波场和隧道反射波场)的线性叠加[20]。但由于山岭隧道所处场地的地面起伏不平，所以是极不规则而复杂的反射面，导致顺层岩体隧道所处场地的地面反射波场亦极不规则且高度依赖于地面轮廓曲线，即具有特殊性；相反，自由波场和隧道反射波场却具有一般性。因此，总波场仅考虑入射波场和隧道反射波场。

地震波对隧道的入射位置有可能在隧道的任何位置，但当地震波由隧道底部入射时，准纵波qP的纵波分量平行于隧道横断面对称轴，准横波qSV的横波分量垂直与隧道横断面对称轴，隧道衬砌关于断面对称轴对称，这可以有效地呈现因岩层各向异性而产生的衬砌响应不对称性或非反对称性，进而根据响应的不对称性或非反对称性研究岩层各向异性对隧道地震响应的影响，因此，设定地震波由隧道底部入射。

由此建立的计算模型如图2所示。有限元模型中隧道衬砌单元划分及编号如图3所示，其中A—H为位移监测点。

图2　平面有限元模型示意图

图3　衬砌单元编号及监测点

2　地震波参数

选取汶川地震时的卧龙波，提取其中振动最剧烈的10～21 s时段的波段，进行滤波和基线校正，得到的位移时程和速度时程如图4所示，将其作为输入模型的地震波。

图4　入射波的位移和速度时程曲线

3　顺层岩体中地震波的输入方法

3.1　顺层岩体中地震波的波动特征

1)波动的平面应变特征

根据文献[21]可知，当地震波入射方向垂直于顺层岩体隧道轴线时(见图2)，则qP波或qSV波仅在平面oxy内波动。因此岩体以及隧道的动力响应为平面应变问题，即在z轴方向上岩体以及隧道的应变始终为0。

2)各坐标系的空间关系

根据计算需要引入多个坐标系，其空间关系如图5所示。图5中：ox0y0z0为岩层本构坐标系；oxryrzr为引用文献[21-22]坐标系；oxyz为总体坐标系；平面S1S2S3S4为岩层层面；地震波传播方向的极化角(即传播方向与zr轴正向的夹角)θ=π，方位角(即从正zr轴来看自xr轴按逆时针方向转到传播方向在oxrzr平面内投影所转过的角)φ=0；M为岩体范围内任一质点；εy为正应变；γxy为剪应变；θ0为岩层倾角，即横观各向同性介质对称轴与zr轴正向的夹角，从正yr轴来看顺时针方向为正。

图5　质点振动方向与应变

3)偏振方向和相速度

在坐标系oxryrzr中，可知地震波偏振向量的精确通解[21]，以及地震波相速度的精确解[22]。

3.2　基于黏弹性边界的地震波输入模式

将基于黏弹性边界的地震动输入转化为人工边界结点上等效荷载的公式[23]为

(1)

3.3　计算人工边界上内行场的位移和速度

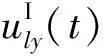
(2)

式中：Δt为入射波从零时刻波阵面(黏弹性下边界)传播到人工边界结点l所需的时间，s；y为人工边界结点l到下人工边界的距离，m；c为cp或csv，其中cp为入射qP波的波速，csw为入射qSV波的波速，m·s-1。

3.4　人工边界上的等效结点力

3.4.1弹性矩阵的转换

计算中须把坐标系ox0y0z0下的弹性矩阵根据bond变换(Winterstein，1990)[18]转换为总体坐标系oxyz下的弹性矩阵。

3.4.2平面波入射时的应变—应力

根据波动特征可知[21]，波场中某质点M的偏振方向如图5所示，qP波偏振方向与传播方向并不平行，qSV波偏振方向与传播方向并不垂直；又因为介质属于线弹性的，所以，质点振动量可分解为沿x轴和y轴的分量，见图5。

1)入射波引起的应变—应力

根据弹性动力力学，并结合文献[5]中几何方程推导过程可知，当入射波沿y向传播时，y向上的位移分量u0y所引起的应变为拉压应变εy，而x向上的位移分量u0x所引起的应变为剪应变γxy，也见图5。应变的计算公式为

(3)

相应的应力计算公式为

(4)

式中：σx为x向的正应力；σy为y向的正应力；τxy为剪应力，N·m-2；c11，c14，…，c44为横观各向同性介质在总体坐标系oxyz下的刚性系数，N·m-2。

对于式(3)：当qP波入射时，由于qP波在垂直于传播方向上的分量以横波的波速传播，即qP波会不断激发新的横波，而被激发的横波又与纵波交织在一起，横波和纵波的耦合会导致研究者难以观察qP波的纵波分量所产生的地震响应的规律，且该横波分量较小，故在模拟qP波地震响应时，略去其横波部分，即令γxy=0；当qSV波入射时，由于qSV波在平行于传播方向上的分量以纵波的波速传播，即qSV波会不断激发新的纵波，而被激发的纵波又与横波交织在一起，横波和纵波的耦合会导致研究者难以观察qSV波的横波分量所产生的地震响应的规律，且该纵波分量较小，故在模拟qSV波地震响应时，略去其纵波部分，即令εy=0。

3.4.3人工边界上等效结点力的计算

最后，计算不同平面地震波作用下隧道结构的响应时，针对不同的平面波类型，将式(4)中各人工边界结点l的应力与其所代表的边界面积As相乘，即可得出该点的等效结点力。

4　qP波入射时岩层各向异性对隧道地震响应不对称性的影响

4.1　qP波入射工况设计

选取qP波的10种工况进行计算，各工况的参数详见表2。其中工况编号约定：以qP-D1-30°为例，qP为地震波类别，D1为地层标号，30°为岩层倾角；其余类推。从表2可知：从D1到D5组顺层岩体，各工况横波分量的偏振向量依次增大，但均小于0.22，所以将其略去，仅采用纵波分量的偏振向量进行计算。

表2　qP波入射时各工况的相速度和坐标系oxy下偏振量

4.2　弯矩包络结果与分析

各工况下隧道弯矩的包络图如图6所示。由图6可知：同一岩层倾角时，各工况下隧道弯矩包络图极为相似；且倾角为30°时，左拱脚弯矩大于右拱脚，而倾角为60°时，却是右拱脚弯矩大于左拱脚。又据拱脚弯矩包络数据可知，各工况拱脚弯矩极值，数值不等，时间不同。

分析该不对称性与岩层各向异性的关系，消除地震响应幅度随岩层强度降低而增强所产生的影响，定义参数左右弯矩差之比δW，其计算公式为

图6　qP波入射时各工况下的隧道弯矩包络图

(5)

式中：ML和MR分别为左、右拱脚的弯矩。

取同时刻拱脚弯矩的极大值和极小值，采用式

图7　不同地层的左右弯矩差之比(包络)

图8　不同地层的左右弯矩差之比(同时)

4.3　相对位移结果与分析

断面内各测点间的相对位移见表3。表3中：dBG为同时刻测点B和测点G之间的相对位移；其余类推；测点间距离相对原始距离变大为正，反之为负。由表3可知：以工况qP-D1-30°为例，在6.68和8.18 s时，其相对位移左右不对称；在6.68 s时，衬砌在B到G方向处于拉伸状态，而在C到F方向却处于压缩状态；在8.19 s时，衬砌在B到G方向处于压缩状态，而在C到F方向却处于拉伸状态；其余工况的规律相同，只是不同地层，数值不同。

表3　相对位移对照表

续表3　相对位移对照表

为分析该不对称性随岩层各向异性变化的规律，定义参数位移差之比δS，其计算公式为

(6)

图9　不同地层的位移差之比曲线(同时)

5　qSV波入射时岩层各向异性对隧道地震响应非反对称性的影响

5.1　qSV波入射工况设计

选取qSV波的10种工况进行计算，各工况的参数详见表4。从表4可知：从D1到D5组顺层岩体，各工况纵波分量的偏振向量依次增大，但均小于0.22，所以将其略去，仅采用横波分量的偏振向量进行计算。

表4qSV波入射时各工况的相速度和坐标系oxy下偏振量

工况相速度/(m·s-1)偏振量的纵波分量py偏振量的横波分量pxqSV⁃D1⁃30°165460075183-0997169qSV⁃D2⁃30°158040102464-0994736qSV⁃D3⁃30°150060134132-0990963qSV⁃D4⁃30°141350170611-0985338qSV⁃D5⁃30°131620211723-0977329qSV⁃D1⁃60°165140056593-0998397qSV⁃D2⁃60°156690090463-0995899qSV⁃D3⁃60°147070125842-0992050qSV⁃D4⁃60°136080161781-0986826qSV⁃D5⁃60°123410196516-0980500

5.2　弯矩包络结果与分析

各工况下隧道弯矩包络图如图10所示。拱脚弯矩峰值及对应的单元和时间见表5；同时刻拱脚弯矩见表6；弯矩方向垂直纸面向外为正，反之为负。由图10和表5可知：弯矩极值均位于拱脚处，且数值非反对称；同一岩层倾角时，包络图相似且相近。

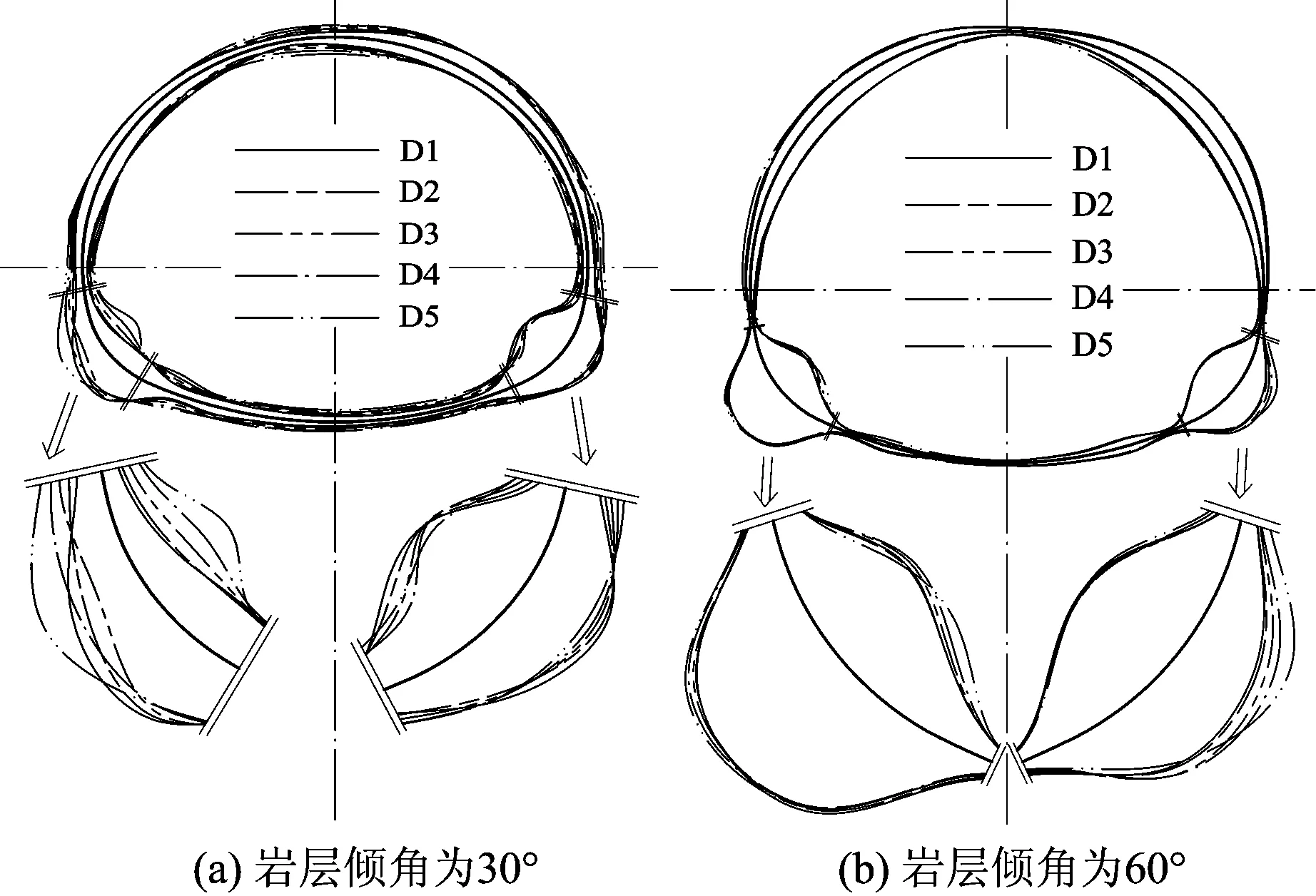
图10　qSV波入射时各工况下的隧道弯矩包络图

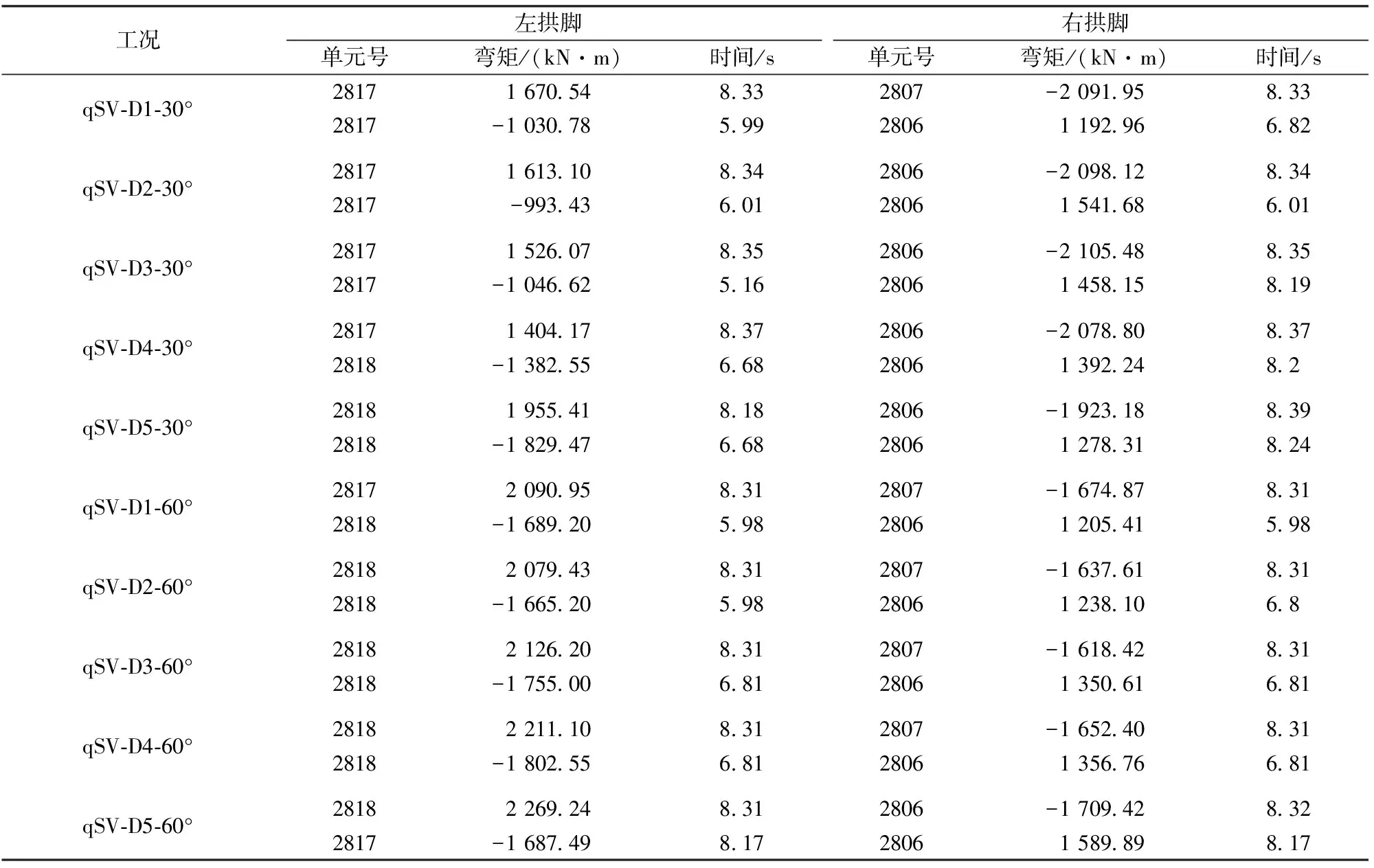
工况左拱脚右拱脚单元号弯矩/(kN·m)时间/s单元号弯矩/(kN·m)时间/sqSV⁃D1⁃30°28171670548332807-2091958332817-1030785992806119296682qSV⁃D2⁃30°28171613108342806-2098128342817-993436012806154168601qSV⁃D3⁃30°28171526078352806-2105488352817-1046625162806145815819qSV⁃D4⁃30°28171404178372806-2078808372818-138255668280613922482qSV⁃D5⁃30°28181955418182806-1923188392818-1829476682806127831824qSV⁃D1⁃60°28172090958312807-1674878312818-1689205982806120541598qSV⁃D2⁃60°28182079438312807-1637618312818-166520598280612381068qSV⁃D3⁃60°28182126208312807-1618428312818-1755006812806135061681qSV⁃D4⁃60°28182211108312807-1652408312818-1802556812806135676681qSV⁃D5⁃60°28182269248312806-1709428322817-1687498172806158989817

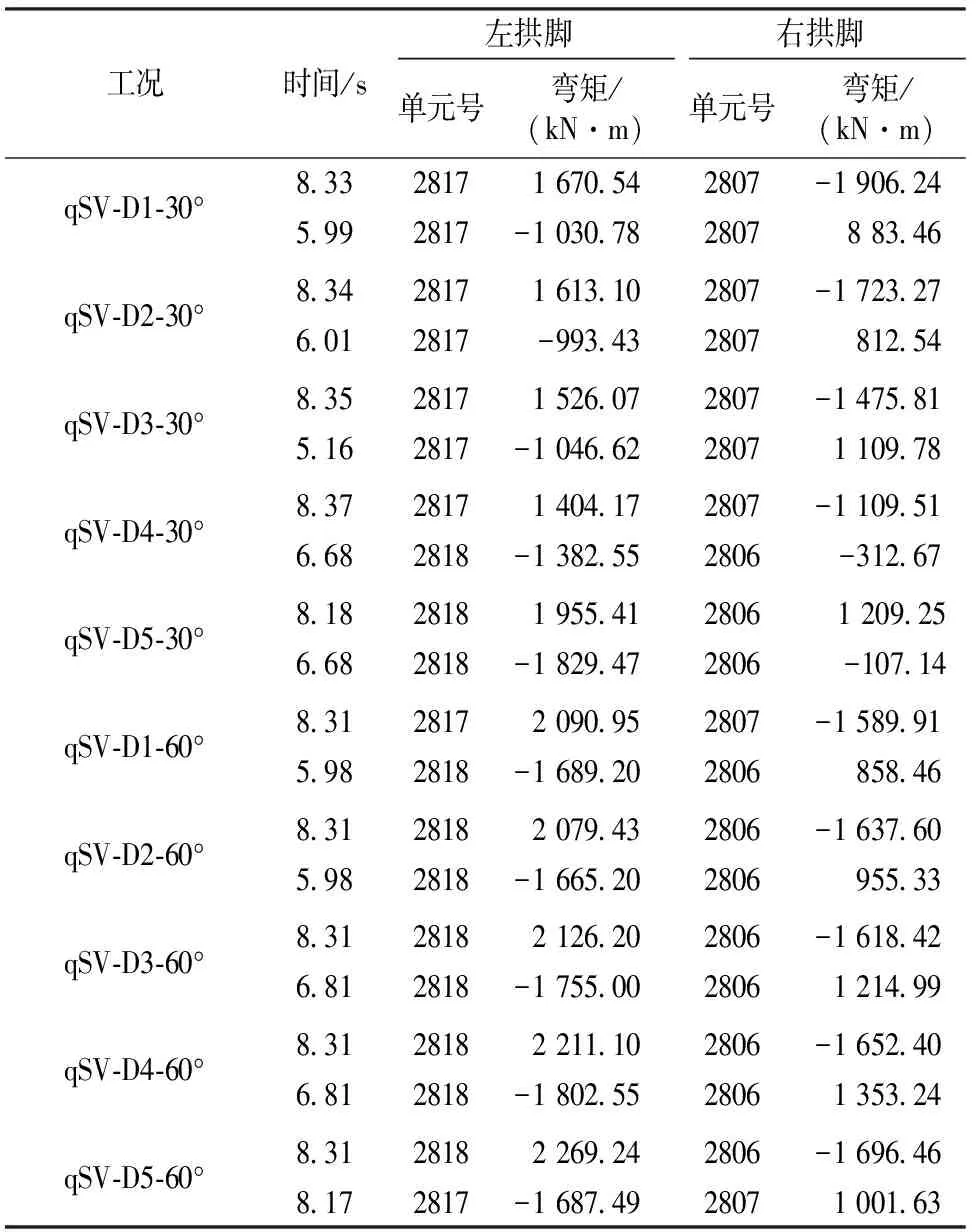
表6　qSV波入射时各工况下同时刻左右弯矩对照表

注：“时间”取左拱脚达到弯矩峰值的时刻；右拱脚的单元号取与左拱脚对称的单元号。

为分析该非反对称性随岩层各向异性变化的规律，定义参数左右弯矩和之比ξW，其计算公式为

(7)

图11　不同地层的左右弯矩和之比(包络)

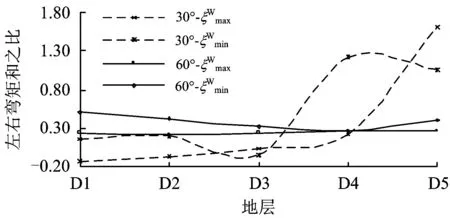
图12　不同地层的左右弯矩和之比(同时)

5.3　相对位移结果与分析

各工况的相对位移见表7。由表7可知：以工况qSV-D1-30°为例，在5.99和8.33 s时，其相对位移左右非反对称；在5.99 s时，衬砌在B到G方向处于压缩状态，在C到F方向却处于拉伸状态，但数值绝对值却不等；在8.33 s，衬砌在B到G方向处于拉伸状态，在C到F方向却处于压缩状态，但数值绝对值却不等；其余工况的规律相同，衬砌相对位移均左右非反对称，只是不同地层，数值不同。

为分析该非反对称性随岩层各向异性变化的规律，定义参数位移和之比ξS，其计算公式为

(8)

取表7中数据，采用式(8)计算位移和之比，绘制图13。由图13可知：在岩层倾角为60°时，该左右非反对称性随岩层各向异性的增强而增大，近似呈线性关系；而在岩层倾角为30°时，非反对称性却并未随岩层各向异性的增强而增大，而是先减小后增大，呈非线性。可见，隧道衬砌变形随地层各向异性的变化规律不统一，视岩层倾角而定。

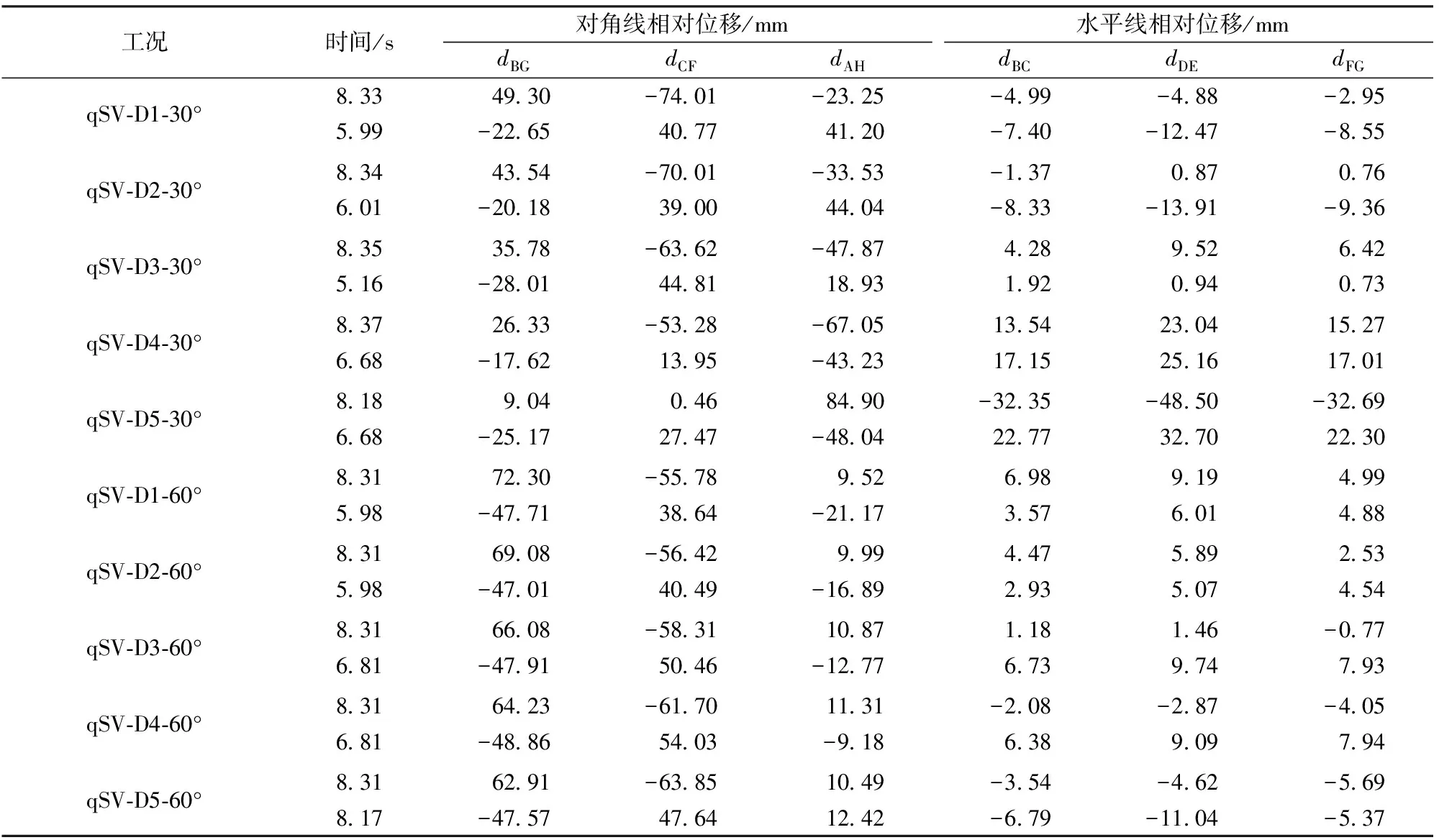
表7　qSV波入射时各工况下的相对位移对照表

注：“时间”的选取同表6。

图13　不同地层的位移和之比曲线(同时)

6　结　论

(1)地震qP波以平面波从隧道底部入射时，随着岩层各向异性的增强，同一时刻，隧道地震响应的不对称性总体上逐渐增大，且服从近似线性关系；但对不同时刻的地震响应包络而言，却无明确而统一的规律，视岩层倾角而定。

(2)地震qSV波以平面波从隧道底部入射时，隧道地震响应的非反对称性随岩层各向异性的变化缺乏统一明确的规律，视岩层倾角而定。

[1]OKAMOTO Shunzo. Introduction to Earthquake Engineering [M]. 2nd Ed. Tokyo：University of Tokyo Press，1984.

[2]SHARMA S，JUDD W R. Underground Opening Damage from Earthquakes [J]. Engineering Geology，1991，30(3/4)：263-276.

[3]吉随旺，唐永建，胡德贵，等. 四川省汶川地震灾区干线公路典型震害特征分析[J].岩石力学与工程学报，2009，28(6)：1250-1260.

(JI Suiwang，TANG Yongjian，HU Degui，et al. Analysis of Typical Seismic Damages of Highways in Wenchuan Earthquake-Induced Hazard Areas in Sichuan Province[J].Chinese Journal of Rock Mechanics and Engineering，2009，28(6)：1250-1260. in Chinese)

[4]胡鸿运，周晓军，汪精河. 顺层隧道地震响应的波动方法研究[J].岩石力学与工程学报，2017，36(6)：1373-1383.

(HU Hongyun，ZHOU Xiaojun，WANG Jinghe. A Wave Numerical Method for Seismic Response of Tunnels in Bedding Strata[J]. Chinese Journal of Rock Mechanics and Engineering，2017，36(6)：1373-1383. in Chinese)

[5]ST JOHN C M，ZAHRAH T F. Aseismic Design of Underground Structures[J]. Tunnelling and Underground Space Technology，1987，2(2)：165-197.

[6]YOUSSEF M A HASHASH, JEFFREY J HOOK, BIRGER SCHMIDT, et al. Seismic Design and Analysis of Underground Structures[J]. Tunnelling and Underground Space Technology，2001，16(4)：247-293.

[7]ESMAEILI M， VAHDANI S， NOORZAD A. Dynamic Response of Lined Circular Tunnel to Plane Harmonic Waves[J]. Tunnelling and Underground Space Technology，2006，21(5)：511-519.

[8]黄娟,彭立敏,李晓英,等.隧道振动响应研究进展[J].中国铁道科学，2009，30(2):60-65.

(HUANG Juan, PENG Limin, LI Xiaoying, et al. Progress Made in the Research on the Vibration Response Induced by Trains Running Through Tunnels[J]. China Railway Science，2009，30(2)：60-65. in Chinese)

[9]PARK Kyung-ho,TANTAYOPIN Kullachai,TONTAVANICH Bituporn, et al. Analytical Solution for Seismic-Induced Ovaling of Circular Tunnel Lining under No-Slip Interface Conditions: a Revisit[J]. Tunnelling and Underground Space Technology，2009，24(2)：231-235.

[10]陈磊,陈国兴,李丽梅.近场和远场地震动作用下双层竖向重叠地铁隧道地震反应特性[J].中国铁道科学，2010，31(1):79-86.

(CHEN Lei，CHEN Guoxing，LI Limei. Seismic Response Characteristics of the Double-Layer Vertical Overlapping Metro Tunnels under Near-Field and Far-Field Ground Motions[J]. China Railway Science，2010，31(1)：79-86. in Chinese)

[11]CILINGIR Ulas，GOPAL MADABHUSHI S P. A Model Study on the Effects of Input Motion on the Seismic Behaviour of Tunnels[J]. Soil Dynamics and Earthquake Engineering，2011，31(3)：452-462.

[12]朱正国,余剑涛,隋传毅,等.高烈度活断层地区隧道结构抗震的综合措施[J].中国铁道科学，2014，35(6)：55-62.

(ZHU Zhengguo, YU Jiantao, SUI Chuanyi, et al. Comprehensive Seismic Measures for Tunnel Structure in the Area of High Intensity Active Fault[J]. China Railway Science，2014，35(6)：55-62. in Chinese)

[13]赵晓勇,杨长卫,张建经.地震作用下盐水沟隧道破坏成因研究[J].中国铁道科学，2015，36(5)：61-67.

(ZHAO Xiaoyong, YANG Changwei, ZHANG Jianjing. Failure Mechanism of Yanshuigou Tunnel under Earthquake Action[J]. China Railway Science，2015，36(5)：61-67. in Chinese)

[14]安军海,陶连金,李积栋,等.地铁双层交叉隧道非线性地震响应分析[J].中国铁道科学，2015，36(3)：66-72.

(AN Junhai, TAO Lianjin, LI Jidong, et al. Nonlinear Seismic Response of Double-Decked Intersecting Metro Tunnel[J]. China Railway Science，2015，36(3)：66-72. in Chinese)

[15]晏启祥,周侣,王春燕,等.用于深埋圆形盾构隧道地震效应分析的2种拟静力解析解的对比研究[J].中国铁道科学，2015，36(2)：45-51.

(YAN Qixiang, ZHOU Lü, WANG Chunyan, et al. Comparative Study on Two Pseudo-Static Analytical Solutions to Seismic Effect for Deep Buried Circular Shield Tunnel[J]. China Railway Science，2015，36(2)：45-51. in Chinese)

[16]胡聿贤.地震工程学[M]. 2版.北京：地震出版社，2006：16-17.

[17]THOMSEN L. Weak Elastic Anisotropy [J]. Geophysics，1986，51(10)：1954-1966.

[18]WINTERSTEIN D F. Velocity Anisotropy Terminology for Geophysicists[J]. Geophysics，1990，55(8)：1070-1088.

[19]刘晶波，杜义欣，闫秋实. 黏弹性人工边界及地震动输入在通用有限元软件中的实现[J]. 防灾减灾工程学报，2007， 27(增刊)：37-42.

(LIU Jingbo, DU Yixin, YAN Qiushi. Realization of Viscoelastic Boundary and Seismic Input in Finite Element Software[J]. Journal of Disaster Prevention and Mitigation Engineering，2007，27(Supplement)：37-42. in Chinese)

[20]廖振鹏. 工程波动理论导论[M]. 2版. 北京：科学出版社，2002：141-155.

[21]梁锴. TI介质地震波传播特征与正演方法研究[D].北京：中国石油大学，2009：20-29.

(LIANG Kai.The Study on Propagation Feature and Forward Modeling of Seismic Wave in TI Media [D]. Beijing：China University of Petroleum，2009：20-29. in Chinese)

[22]吴国忱,梁锴,戚艳平. 三维TTI介质相速度和群速度[J]. 地球物理学进展，2009，24(6)：2097-2105.

(WU Guochen, LIANG Kai, QI Yanping. Phase Velocity and Group Velocity in 3D TTI Media [J]. Progress in Geophysics，2009，24(6)：2097-2105. in Chinese)

[23]何建涛，马怀发，张伯艳，等. 黏弹性人工边界地震动输入方法及实现[J]. 水利学报，2010，41(8)：960-969.

(HE Jiantao，MA Huaifa，ZHANG Boyan，et al. Method and Realization of Seismic Motion Input of Viscous-Spring Boundary[J]. Journal of Hydraulic Engineering，2010，41(8)：960-969. in Chinese)