基于发展学生核心素养的高中数学教学思考

广东省东莞市南城中学(523077)　陈立

修订后的普通高中课程标准指出:数学核心素养是数学课程目标的集中体现,是学生在数学学习的过程中逐步形成的.数学核心素养是具有数学基本特征的、适应个人终身发展和社会发展需要的人的思维品质与关键能力.高中阶段数学核心素养包括:数学抽象、逻辑推理、数学建模、直观想象、数学运算和数据分析.

人民教育出版社章建跃博士指出:学好数学是发展数学核心素养的前提,把数学教好是落实数学核心素养的关键.教师以数学知识为载体发展学生的核心素养.在数学知识的教学中寻找发展学生核心素养的途径.为此,本文从概念教学、例题教学、试卷讲评等方面谈一谈发展学生核心素养的一些思考.

1　在概念教学中发展学生的核心素养

1.1　概念教学

概念教学通常是指概念课以及概念后继课的教学.概念教学是数学教学最重要的任务.在概念教学中可以发展学生的多个核心素养,尤其是发展学生的数学抽象、逻辑推理等核心素养.下面以“二项分布的概念”教学为例,研究在概念教学中发展学生核心素养的一些做法.

1.2　“二项分布的概念”教学示例

(1)二项分布概念的引入

思考1抛掷一枚图钉,针尖向上的概率为p,连续掷3次图钉,出现k(k=0,1,2,3)次针尖向上的概率是多少?

思考2抛掷一枚图钉,针尖向上的概率为p,连续掷4次图钉,出现k(k=0,1,2,3,4)次针尖向上的概率是多少?

设计说明思考1、2的教学价值主要在于发展学生的数学抽象、逻辑推理和数学运算素养.依据学生的认知水平,学生能够求出思考1中k=0,1,2,3时的概率,或求出思考2中k=0,1,2,3,4时的概率.但是学生能否把答案表述为或呢?教师可根据课堂实情灵活应对.

(2)二项分布概念的生成

问题1根据思考1、思考2得到的答案,你能否给出一个一般性结论?

设计说明问题1的教学价值主要在于发展学生的数学抽象素养.预计学生基于思考1、2的答案写出“抛掷一枚图钉,针尖向上的概率为p,连续掷n次图钉,出现k次针尖向上的概率是P(X=k)=Cknpk(1−p)n−k,k=0,1,2,···,n”这个结论,这时教师可以追问:只有抛掷图钉才有这个结论吗?能否把结论描述的更具一般性?教师根据学生回答的情况小结:抛掷一枚图钉n次也就是做独立重复试验n次,“针尖向上”是抛掷一枚图钉的一个试验结果,把“针尖向上”一般化为“试验中事件A发生,或事件A成功”.教师通过以上形式,达成这个环节的目标已经水到渠成,这时教师准确板书二项分布的概念,并强调相关记号.

思考 3对比0,1,2,···,n与表示二项式定理的公式,你能看出它们之间的联系吗?

设计说明思考3的教学价值主要在于发展学生的逻辑推理素养.它可以让学生知道k=0,1,2,···,n就是[(1−p)+p]n展开式的各项,因此称为二项分布,同时,学生也容易看出这个思考不仅强化了学生对二项分布的理解,而且强化了学生对分布列性质=1的认识.

(3)二项分布概念的应用

思考4二项分布与两点分布有何关系?

设计说明思考4的教学价值主要在于发展学生的逻辑推理素养.思考4的价值还在于让学生了解两点分布是最简单的二项分布,是二项分布在n=1时的特例.

问题2①某射手每次击中目标的概率都是0.8,请问这名射手在10次射击中,击中k次的概率是多少?说明理由.

②某工厂生产的灯泡,其使用寿命超过500小时的概率是0.8,请问购买5个这样的灯泡有4个使用寿命超过500小时的概率是多少?

设计说明问题2的教学价值主要在于发展学生的数学抽象、逻辑推理和数学运算素养.①目的是使学生进一步理解独立重复试验的含义和二项分布的概念;②目的是使学生了解n次独立重复试验中事件A可以包含无数个结果.

问题3(2017·全国I卷·理科数学·19)为了监控某种零件的一条生产线的生产过程,检验员每天从该生产线上随机抽取16个零件,并测量其尺寸(单位:cm).根据长期生产经验,可以认为这条生产线正常状态下生产的零件的尺寸服从正态分布N(µ,σ2).

(1)假设生产状态正常,记X表示一天内抽取的16个零件中其尺寸在(µ−3σ,µ+3σ)之外的零件数,求P(X≥1)及X的数学期望;(2)略.

附:若随机变量Z服从正态分布N(µ,σ2),则P(µ−0.09.

设计说明问题3的考试价值主要在于发展学生的数学抽象、逻辑推理和数学运算素养.问题3是2017年全国高考I卷理科数学第19题,这个问题非常巧妙的考查了二项分布的概念.考生解答第(1)问的困难在于能否抽象出X～B(16,0.0026).当然,该题对考生的阅读理解能力和数据处理能力要求也很高.

数学概念是数学的逻辑起点,是数学知识的基础,是数学思想与方法的载体.数学概念怎样引入、怎样生成,为引入和生成数学概念而设置的问题和思考价值何在,如何让学生在数学概念形成的过程中发展核心素养,这需要我们的智慧,更需要我们去认真思考.

2　在例题教学中发展学生的核心素养

2.1　例题教学

例题教学是数学教学的重要环节,例题教学也是数学概念、数学原理和数学命题等理论知识教学的延续.处理好例题教学有助于学生理解和掌握数学知识,培养学生的能力,发展学生的数学核心素养.例题教学需要处理好以下几个方面:

(1)例题的教学价值.

(2)例题所承载的功能.

(3)例题的变式.变式题以加强对例题的理解为目标.

(4)例题的延伸.主要考虑从近几年高考题、名校模拟题、期末检测题以及数学竞赛题等试卷中选相近题目作为例题的延伸.

2.2　例题教学示例

示例1(人教A版·必修五·2.3例4)已知等差数列5,·的前n项和为Sn,求使得Sn最大的序号n的值.

(1)教学价值:依托相关知识储备写出Sn,利用二次函数求最值的方法求出n的值,其教学价值主要在于发展学生的数学运算和逻辑推理素养.

(2)功能:进一步加强对等差数列概念、等差数列通项公式、等差数列前n项和公式的理解,也是等差数列前n项和公式的一个应用.

(3)变式

①已知等差数列{an}的通项an=其前n项和为Sn,求使得Sn最大的序号n的值.

设计这个题目的目标是引导学生从另外一个角度研究示例1.

变式①可追问学生:若将题中的“等差数列”4个字去掉,怎样解答?目标是培养学生思维的严密性,发展学生的逻辑推理素养.

②已知等差数列{an}的前n项和为Sn,且有a1+a3+a5=105,a2+a4+a6=99,求使得Sn最大的序号n的值.

设计这个题目的目标是加强学生对示例1和变式①解法的理解.

(4)延伸

(2014·江西高考文科·13)在等差数列{an}中,a1=7,公差为d,前n项和为Sn,当且仅当n=8时Sn取得最大值,则d的取值范围为___.

图1

示例 2(人教 A版 ·选修 2-2·2.1.1例4)如图1所示,有三根针和套在一根针上的若干金属片.按下列规则,把金属片从一根针上全部移到另一根针上.i)每次只能移动1个金属片;ii)较大的金属片不能放在较小的金属片上面.试推测:把n个金属片从1号针移到3号针,最少需要移动多少次?

(1)教学价值:依托相关知识储备,运用合情推理猜想出把个金属片从1号针移到3号针最少需要的次数,或总结出把n个金属片从1号针移到3号针最少需要的次数的递推公式,其教学价值主要在于发展学生的逻辑推理、数学抽象、数据处理素养.

(2)功能:进一步加强学生应用归纳推理、类比推理解决实际问题的能力,是合情推理的一个具体应用,也是已知数列的递推公式求通项公式的一个实例.

(3)变式:示例2对学生来说难度较大,此处不用再变式,直接让学生归纳解答示例2的关键和启示,然后一起分享.目标是形成共识:以最少次数把n个金属片从1号针移到3号针,也就是以最少次数把1号针前n−1个金属片移到2号针,再把第n个金属片1步移到3号针,然后以最少次数把2号针上的n−1个金属片移到3号针.

(4)延伸

①(2010·高中数学联赛广东省预赛·5)一只虫子沿三角形铁圈爬行,在每个顶点,它都等机会地爬向另外两个顶点之一,则它在n次爬行后恰好回到起始点的概率为____.

②(2011·高中数学联赛广东省预赛·8)10名学生站成一排,要给每名学生发一顶红色、黄色或者蓝色的帽子,要求每种颜色的帽子都要有,且相邻的两名学生帽子的颜色不同.则满足要求的发帽子的方法共有___种.

以上两题都有难度,其难度在于能否把问题转化为示例2中求递推公式的方法进行求解.

示例3(人教A版·选修2-3·3.1例2)一只红铃虫的产卵数y和温度x有关.现收集了7组观测数据如下表,试建立y关于x的回归方程.

__温度 x/°C 21__23__25__27__29___32___35__产卵数y/_个____7___11__21__24__66__115__325

(1)教学价值:依托相关知识储备,建立y关于x的回归方程,其教学价值主要在于发展学生的数据分析、数学建模、数学运算素养.此外,从观察散点图到确定回归模型的形式的过程中使示例3也有发展学生直观想象、数学抽象和逻辑推理素养的教学价值.

(2)功能:深入体会统计方法的特点,初步了解非线性回归模型的建模、求解.示例3也是判断不同模型的拟合效果的一个实例,暗示了寻求拟合效果更好的模型是统计分析的目标.

(3)变式:示例3对学生来说难度很大,变式题目可布置为学生的课外作业.课堂上,引导学生总结利用观测数据建立回归模型的步骤,让学生谈一谈统计学对于建模所追求的目标.

(4)延伸

①(2015·全国卷I理科·19)某公司为确定下一年度投入某种产品的宣传费,需了解年宣传费x(单位:千元)对年销售量y(单位:t和年利润z(单位:千元)的影响.对近8年的年宣传费xi和年销售量yi(i=1,2,···,8)数据作了初步处理,得到下面的散点图及一些统计量的值.

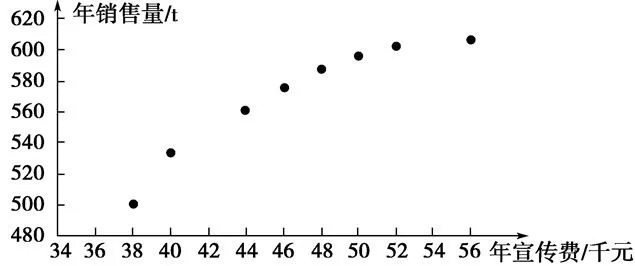
图2

¯x ¯y ¯w 8∑(xi−¯x)28∑(wi−¯w)28∑(xi−¯x)(yi−¯y)8∑(wi−¯w)(yi−¯y)i=1 i=1 i=1 i=1 46.6__563__6.8_____289.8_________1.6_____________1469______________108.8_______

表中wi=

(1)根据散点图判断,y=a+bx与y=哪一个适宜作为年销售量y关于年宣传费x的回归方程类型(给出判断即可,不必说明理由);

(2)根据(1)的判断结果及表中数据,建立y关于x的回归方程;

(3)已知这种产品的年利润z与x,y的关系为z=0.2y−x,根据(2)的结果回答下列问题:(i)当年宣传费x=49时,年销售量及年利润的预报值是多少?(ii)当年宣传费x为何值时,年利润的预报值最大?

附:略.

如果当年参加高考的考生平时认真思考过示例3,或者说教师在讲示例3时让学生有过比较成功的体验,那么正确求解这道高考题就不是问题.

教材中每个例题都有各自的价值,并且承载不同的功能,有效的例题教学是发展学生核心素养的重要途径.

3　在试卷讲评中发展学生的核心素养

3.1　试卷讲评

试卷讲评是高中数学的重要课型.平时的周周练、月考,主要功能是检测学生的学习效果,了解学生的学习情况.教师在讲评试卷之前要清楚哪些问题是自己的问题,怎么调整,哪些问题是学生的问题,怎么“补缺”.期末统考、数学竞赛和高考与平时的考试有所不同,这些试题还要研究它们的导向性.评卷时处理好典型错题的变式,或典型错题的一题多解.

3.2　试卷讲评示例

示例1(高一第一学期·周周练·16)设偶函数f(x)的定义域为[−5,5],若当x∈[0,5]时,f(x)的图象如右图,则不等式x···f(x)＞0的解集是____(结果用区间来表示).

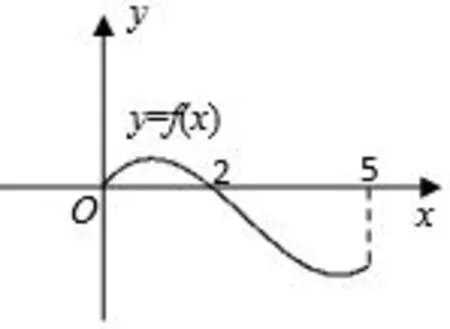
图3

(1)存在问题:这道题主要考查偶函数的概念和利用函数的图象性质求解不等式.题目难度不大,考前预估得3分,考完后统计仅得0.12分,大大低于预期得分.出现这种情况,教师在评卷时需要解决好以下问题:

①对学情把握不准,需要加大对学生的关注度.

②学生数形结合思想的应用意识薄弱.教师在评卷时,让学生解答事先准备好的变式题,并让求解完整的学生说解法,教师仅作必要的补充.

(2)考试价值:利用图形探索和解决不等式问题的考试价值主要在于发展学生的直观想象和逻辑推理素养.

示例2(2017·东莞市第二学期期末·高二文科数学·16)已知△ABC中,∠B=30°,AC=1,D为BC上的中点,则AD的最小值为____.

(1)存在问题:这道题主要是考查正、余弦定理的应用.我校没有学生答对这道题.出现这种情况,教师在评卷时需要解决好以下问题:

①教师对教材研究的不深入,需要加强.主要表现为:i)这道题是由人教A版 ·必修五·习题1.2第14题改编而来的.学生利用题设给出的条件很容易得到然后再应用正弦定理和正弦函数的性质解答这道题.讲评前要了解学生答题受阻在什么地方.ii)应用人教A版·必修五·习题1.1 B组第1题结论,先求出△ABC外接圆半径R=1,讲评前要了解有没有学生这样思考,受阻在哪里?按这个思路该题可转化为:

如图4,内接于半径为1的⊙O,且是优弧ABC上任意一点(不包括A,B),BC上的中线为AD,则AD的最小值为___.

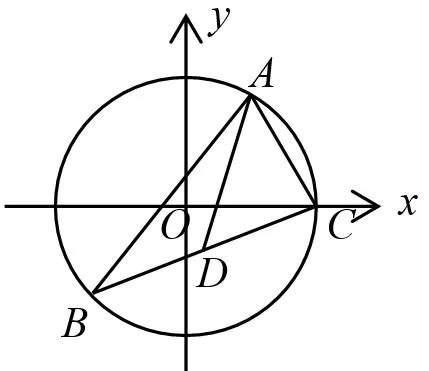
图4

②学生的计算和综合分析能力非常薄弱.试卷讲评时除要求学生掌握上述方法以外,还可以介绍判别式法解答这道题.事实上,求出以后,令c=ma(m＞0),导出然后把AD表示为令k=化简得:

(4k−1)m2−m+4(k−1)=0,由m＞0为实数,那么∆≥0,从而得到(AD)min=

(2)考试价值:利用教材原题或原题的变式作为期末统考题,导向就是提醒老师深入研究教材.这道题的考试价值主要在于发展学生的数学运算、数学抽象和逻辑推理素养.

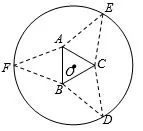
图5

示例3(2017·全国卷I理科·16)如图,圆形纸片的圆心为O,半径为5 cm,该纸片上的等边三角形ABC的中心为O.D,E,F为圆O上的点,△DEC,△ECA,△FAB分别是以BC,CA,AB为底边的等腰三角形.沿虚线剪开后,分别以BC,CA,AB为折痕折起△DEC,△ECA,△FAB,使得D,E,F重合,得到三棱锥.当△ABC的边长变化时,所得三棱锥体积(单位:cm3)的最大值为____.

(1)存在问题:由一个平面图形折成三棱锥,这是一道有创新的题目.尽管学生对三棱锥并不陌生,但是,题中的三棱锥是学生根据条件抽象出来的,在自己抽象出的几何体中解决问题,这对学生来说还是有难度的.学生可能对三棱锥中的数量关系、位置关系模糊,也可能是算不出.事实上,这道题所给的模型满足:等边△DEF内接于半径为5cm的圆O,如图6①,等边△ABC内接于小圆O,因为以BC,CA,AB为折痕折起△DEC,△ECA,△FAB后成为三棱锥,所以小圆O可大,但是比大圆O小,如图6②,小圆O也可小,如图6③,直至几乎退化为一个点,如果这样思考的话,可设小圆O的半径为x(0＜x＜5),易知AB=则有折后得到的正三棱锥的高

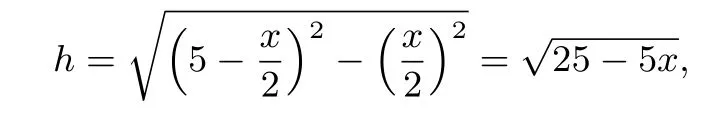
从而

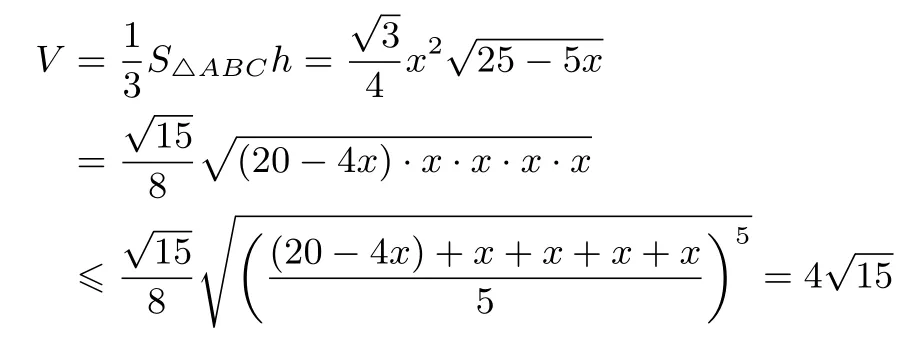
(当且仅当x=4时取等号).

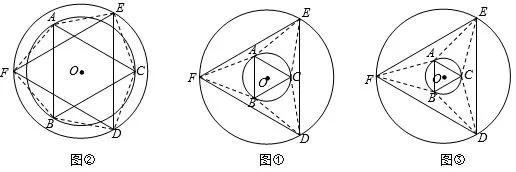
图6

(2)考试价值:把学生熟悉的平面图形,折成学生并不陌生的空间图形来探索和解决问题.其考试价值主要在于发展学生的直观想象、数学抽象、逻辑推理和数学运算等核心素养.该题对教学的导向有:加强阅读理解能力、运算求解能力、空间想象能力的培养.

试卷讲评的重点是为了解决教与学存在的问题,在试卷讲评中发展学生的核心素养是我们的目标.透过试题看方向、研究试题的考试价值也是试卷讲评的重要内容.

结束语

修订后的高中课程标准在课程目标中指出:学生通过高中数学的学习,学会用数学眼光观察世界,发展数学抽象和直观想象素养;学会用数学思维分析世界,发展逻辑推理和数学运算素养;学会用数学语言表达世界,发展数学建模和数据分析素养.以发展学生的核心素养为目标的理念开始走进我们的教学,笔者之所以选择概念教学、例题教学、试卷讲评等来探讨关于发展学生核心素养的问题,是因为它们是数学课堂教学的重中之重,至于怎么更加有效的发展学生的核心素养是值得我们继续研究的课题.