基于APOS理论的初中数学概念和公式的教学探究*

广东省广州市第十六中学(510000)　林晓君

APOS理论是美国学者杜宾斯基等人提出的一种建构主义的数学学习理论,它主张建构要具有层次性的观点为数学概念教学的逐层渐进提供了理论基础,并且具有现实的可操作性.APOS 由 “Action(操作)”“Process(过程)“Object(对象)”和“Schema(图式)”四个英文单词的首字母组合而成,杜宾斯基认为数学概念的学习要经历这四个活动阶段.

数学概念的教学有两种模式,概念的形成和概念的同化,前者更注重概念的建构过程,可以用APOS理论进行指导;而数学公式的教学也有两种形式,例子到原理,原理到例子,前者是一种发现式学习,符合建构主义学习理论.因此本文将把APOS理论运用到初中数学的概念和公式的教学上,通过具体的例子对四个阶段的教学策略进行初步的探究.

一、“操作(A)阶段”

在学习新知识之前,教师基于学生已有认知基础,通过一些数学活动,如动手操作、猜想、回忆、计算、推理等,让学生通过“操作活动”,亲自体验、感受新知识的直观背景或知识间的关系,为抽象概括提供感性基础.在这个阶段,我们可以通过创设问题情境,或者提出一些需要解决的问题,燃起学生思考的火花,以递进的问题串引发学生的思考.

例1分式概念的引入

(1)长方形的面积为10cm2,长为5cm,则宽为___cm;

长方形的面积为Scm2,长为5cm,则宽为___cm;

长方形的面积为(S+2)cm2,长为5cm,则宽为___cm;

长方形的面积为(S+2)cm2,长为acm,则宽为____cm.

(2)把体积为200cm3的水倒入底面积为Scm2的圆柱形杯中,则水面高度为___cm;

把体积为Vcm3的水倒入底面积为(S+2)cm2的圆柱形杯中,则水面高度为____cm.

分析本环节以常见的生活问题为背景创设问题串.问题的设置从数10到字母S到代数式(S+2),由特殊到一般,让学生感受到分式是解决实际问题的一个重要模型,但它又不是整式,造成了认知冲突,为概念的形成提供感性认识.

例2平方差公式的引入

一个狡猾的园主,把一块边长为a(a＞5)的正方形土地租给张老汉种植.第二年,他对老汉说:“我把土地的一边减少5米,相邻一边增加5米,继续租给你,租金不变,你也不吃亏,你看如何?”老汉一听,觉得好像没亏,就答应了,回到家,他把事情跟邻居一讲,大家都说他亏了,老汉非常吃惊,你知道他为什么吃亏吗?

分析本环节以一道有趣的生活问题为背景创设问题情境,激发学生的解决欲望,为学生带来学习新知识的冲动.为平方差公式的学习提供感性认识.

二、“过程(P)阶段”

在“操作(A)阶段”学生获得了直观感知,在随后的这一阶段,就要对其进行组织和处理,经历观察、联想、归纳和概括等过程,才能实现顿悟和知识的内化,是感性认识逐渐上升到理性认识的阶段.在这一阶段,我们要设置由浅到深的问题,不断的引导学生进行思考,充分暴露思维的过程,才能促进知识的“再创造”.若此过程过于短暂或缺失,将会影响学生的参与度和学习效果,直接影响新知识的概括和生成.

例1分式概念的初步形成

老师提问:以上代数式都是整式吗?不是整式的代数式,它们从形式上有什么共同点?

学生思考,讨论后在小组内交流,教师适当引导,共同得出:

▲式子的共同点:

(1)从整体上看,它们都是由分子、分母与分数线构成,都有的形式.

(2)从分子和分母单独看,分子、分母都是整式,分母中都含有字母.

分析分式的概念实则是一个形式概念,它的形式与分数相同,但本质属性又与分数不同,因为分数属于整式而不是分式,因此引导学生通过类比的方式认识分式的结构特征,揭示分式的本质属性,初步获得分式的概念.

例2平方差公式结构的初步判断

计算以下式子,观察结果有什么特点?你能用文字或符号来表示你的发现吗?

(1)(x+1)(x−1);

(2)(x+3)(x−3);

(3)(3a+2)(3a−2);

(4)(y+4x)(y−4x).

分析学生通过自己的计算,发现了结果刚好为平方差的特点.教师引导学生探究发现平方差公式实则是多项式乘以多项式,但是它的结果没有那么多项,有些项相互抵消了,那究竟相乘的两个多项式存在怎样的结构特征,使得结果刚好为平方差的特点呢?学生通过自己的观察猜测推理,初步揭示了平方差公式的本质,初步获得平方差公式的结构特征.

例3扇形面积公式的猜想

师:你们知道圆周长、弧长公式吗?

生:回答公式C=2πr,l=

师:观察以上公式,弧长和哪些因素有关?弧长与圆周长之间有什么关系?

生:弧长与半径大小和圆心角的度数有关.弧长与圆周长是部分与整体的关系.

师:类比弧长公式,你猜测扇形面积与哪些因素有关?扇形面积与圆面积有什么关系?

生:扇形面积与半径大小和圆心角的度数有关.扇形面积与圆面积是部分与整体的关系.

师:根据圆的面积公式S=πr2,那你能猜想一下扇形的面积公式吗?

分析教师通过让学生回忆圆周长与弧长的公式,得到弧长与圆周长的部分与整体的本质,学生就很容易联想到扇形与圆的部分与整体的本质关系,进而通过类比,利用圆的面积公式猜想到扇形面积公式.

三、“对象(O)阶段”

学生通过前面的程序,在大脑中不断进行描述和反思,抽象概括出新知识所特有的本质特征,对其赋予形式化的定义及内涵,使其达到精确化,在头脑中建立起直观的知识结构形象.是在理性认识的基础上,达到全新认识的阶段.在这一阶段,我们可以运用类比或对比教学,通过正例和反例深化理解,分析它的多元表征,将其判断算法化.

例1《函数》的概念教学,设计了如下四个问题:

①圆周长问题:如果用r表示圆的半径,用C表示圆的周长,那么C=2πr.请指出哪些是变量,变量之间是什么关系?

②汽车以60千米/时的速度匀速行驶,行驶里程为S千米,行驶时间为t小时.请填表,并指出哪些是变量,变量之间是什么关系?

③某一日气温变化的曲线所揭示的气温和时刻的关系如图1所示.指出哪些是变量,变量之间是什么关系?

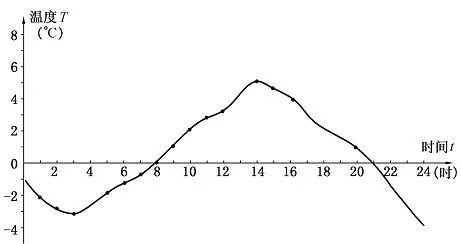
图1

④下列各图中,y关于x是函数关系的是()(可以多选)

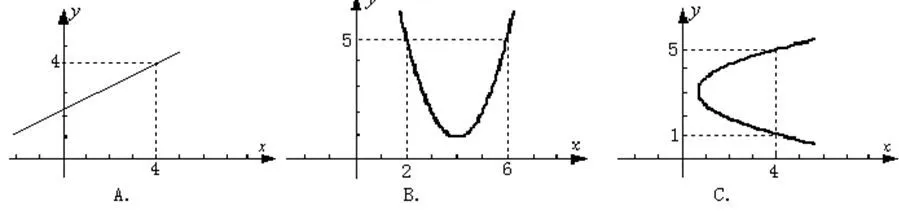
分析以上通过解析式、列表和图像等多种形式的表示,还有正例与反例的对比,帮助学生更好的理解“对于x的每一个值,y都有唯一一个确定的值与其对应”的意思,进而深刻理解“函数”的定义.

例2在推导完全平方公式时,通过情景创设,把一个大正方形(边长为a+b)分成两块小正方形(边长分别为a、b)和两块一样大小的长方形(长和宽分别为a、b),然后让学生计算四块图形的面积,再计算大正方形的面积,通过图形面积计算,让学生等积变换,感受乘法公式的直观解释,推导出完全平方公式:(a+b)2=a2+2ab+b2.

分析学生通过自己动手推理计算,主动探索,在实践中获得知识,从而确定完全平方公式结构猜测的合理性,进而把公式结构化.也有利于数形结合思想的培养和正确理解记住完全平方公式.

四、“图式(S)阶段”

教师提供反映新知识的特例、相关性质等情境给学生探究,学生对其进行深入学习.对前面几个阶段的经历及大脑中原有相关认识的不断的整合、精致,最终实现数学知识的建构,形成综合的心理图式.是理论应用于实际的过程.在这一阶段,我们可以采用题组变式训练或绘制图式形成体系进行教学.

例1学完了四边形和几种特殊的四边形的概念后,我们可以把几个概念之间的关系总结成如下图2,使学生对它们之间的相互转化更清晰.

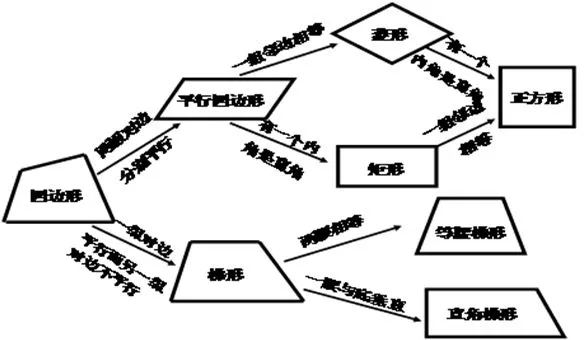
图2

例2化简(x+3)(x−3).

变式1化简(−x−3)(−x+3).

变式2化简(−x+3)(x+3).

变式3化简(−x−3)(x−3).

例3(x+y)2=16,xy=3,则x2+y2=___.

变式1若x−y=4,xy=3,则x2+y2=___.

变式2若(x+y)2=8,xy=1,则(x−y)2=____.

变式3已知(x+y)2=25,(x−y)2=9,则xy=____,x2+y2=___.

变式4已知x+=3,则x2+=___,

分析以上题组变式练习,例2从正面加深了学生对平方差公式结构特征的理解,增强了准确运用公式的能力.例3则是通过两个完全平方公式的变形计算,增强了公式逆用和活用的能力,提高了思维的发散能力.

例4如图,已知Rt△ABC中,∠ACB=90°,CA=CB,有一个圆心角为45°,半径等于CA的扇形CEF绕点C旋转,且直线CE、CF分别与直线AB交于点M、N.

(1)当扇形CEF绕点C在∠ACB的内部旋转,如图3,求证:MN2=AM2+BN2.

(2)当扇形CEF绕点C旋转至如图4的位置时,关系式MN2=AM2+BN2是否仍然成立?若成立,请证明;若不成立,请说明理由.

图3

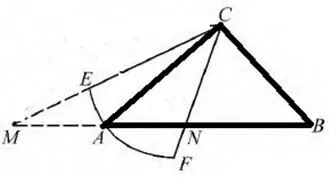
图4

分析勾股定理公式:a2+b2=c2,在应用上一个最重要的前提条件就是直角三角形,因此寻找或构造直角三角形这个数学模型至关重要.让学生学会了数形结合的思想.

在初中数学概念和公式教学中让学生在“操作”中体验、在“程序”中感悟、在“对象”中归纳、在“图式”中升华,分层次逐步递进,体现新知识形成的教学规律和学生的认知规律.学生在整个学习过程中不是线性的,而是螺旋上升,由感性到理性,直至了解新知识的本质,提高了学生的抽象概括能力.最后我们还应该提高学生对数学问题解决的积极性和探索的主动性,培养学生运用数学知识解决实际问题的应用意识和实践能力.