微课在初中数学教学的实践与思考*—以七年级“数学活动-图形变化中的规律探究”为例

广东省广州市南沙东涌中学(511453)　麦凤珊

近年来,各种“微”事物不断涌现,如微博、微信、微电影、微小说、微访谈等,随着“微”队伍的不断壮大,当今社会已经步入了一个“微”时代.微课是在“微”时代应运而生的一种教学手段,其有明确的教学目标、内容短小等特点,微课一般在10分钟以内,以短小精悍的视频为主要表现形式.对于教材中的数学活动课,许多老师认为可有可无,甚至视而不见,导致数学活动课成为课堂教学最为薄弱的环节,究其原因是数学活动课难上,学生收获效果不好.本人在进行七年级“数学活动-图形变化中的规律探究”的教学中采取微课教学,收到了较好的效果,下面以这节课为例谈谈在初中数学教学中使用微课资源的感受.

1　微课应用的实践

1.1　微课制作的原因

人教版七年级教材设置了“数学活动-图形变化中的规律探究”,该数学活动的核心问题是寻求图形的个数与火柴棍根数之间的对应关系,问题的本质是变化与对应.由于观察图形时的角度不同,规律的显现方式不同,所得到的表达形式不同,但经过整式的加减运算后得到的结论是唯一确定的.在拼图的过程中,学生比较容易发现火柴棍根数的变化情况,但要借助观察图形的变化寻找火柴棍的根数与图形的个数n之间的对应关系,还是有一定困难,在总结变化量与n的对应关系时学生也容易出错.所以用整式准确地表示出这种对应关系是本节课的一个难点.本人在以往的教学中发现:由于课时紧张,没有时间去进行反复详细的讲解,使学生对该知识点没有真正的理解好,而用符号表示具体情境中的数量关系和变化规律,对于初一学生而言有一定的难度.针对这一情况,本人思考在教学时应如何帮助学生化解这一难点?经过一番研究思考后,本人认为应用微课进行教学或许会收到较好的效果.

1.2　微课内容设计

微课具备简短精悍、主题突出、反复播放等优势,非常适合本次数学活动教学.本人根据“简单到复杂”、“由特殊到一般”探究方法的设计了以下四个活动.

活动一如图1所示,用火柴棍拼成的一把平放的梯,如果图形中含有1,2或3个节,分别需要多少根火柴棍?如果图形中含有n个节,又需要多少根火柴棍?请把你探究的结论填入表1.

图1

表1

活动二如图2所示,用火柴棍拼成的一些垒好的箱子,如果图形中含有1,2或3个箱子,分别需要多少根火柴棍?如果图形中含有n个箱子,又需要多少根火柴棍?请把你探究的结论填入表2.

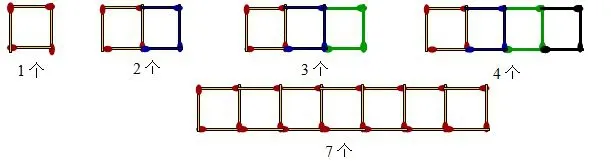
图2

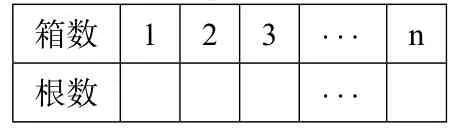
表2

活动三如图所示,用火柴棍拼成一排由三角形组成的图形,如果图形中含有1,2或3个三角形,分别需要多少根火柴棍?如果图形中含有n个三角形,需要多少根火柴棍?请把你探究的结论填入表3.

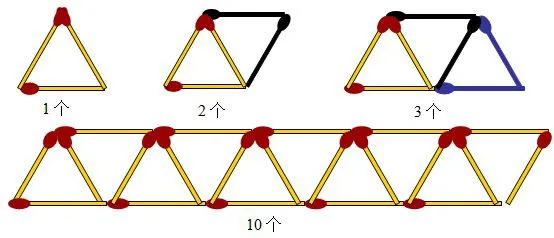
图3

表3

活动四对于活动三,通过观察后,你所发现的规律与其它同学的思考过程是一样吗?请同学们以小组为单位进行讨论.

2　本次微课应用的效果

2.1　反复学习,便于学生理解和吸收

本节数学活动利用微课进行教学,可以反复进行播放,对于课堂收获不佳的学生也可以回去进行再学习.给出按一定规律排列的图形,让学生通过观察、操作、填表、猜想、验证、交流等活动,从而发现隐含于其中的规律,并用含有字母n的式子表示规律.让学生根据图形的特征把较复杂的图形进行不同角度的分解,把图形分解为若干个基本图形后,进而发而其中基本图形个数的递增规律,体会探索规律的一般方法,积累数学活动经验,感悟由特殊到一般的数学思想.同时本活动是从用火柴棒搭建符合一定条件的简单图形开始,到图形的变化和数学思考,让学生感受小小的火柴棒中蕴含着大的智慧,只要你动手操作、动脑思考,会有不少的收获.

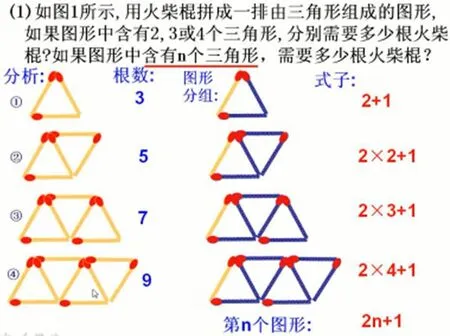
图4

2.2　让学生体验解决问题策略的多样性

数学活动课以活动为主要形式,要求学生参与到活动中去,发现和解决问题,体验和感受活动,让学生积极参与数学活动,在数学活动过程中,合作交流、反思质疑,体验获得成功的乐趣,锻炼克服困难的意志,建立学好数学的自信心.让学生体会进行数学活动的基本方法:提出问题→动手实践→寻求规律→归纳总结.让学生经历发现问题、独立思考、猜想验证、归纳总结这些数学活动,从不同角度观察问题、发现规律,培养应用意识和创新意识.教学中让学生体验解决问题策略的多样性,并尝试评价不同方法之间的差异,从而得到出最优方案.活动四的方法是多样的,通过学生的操作、思考得到下面几种方法:

①从第二个图形起,与前一个图形比,每增加一个三角形,增加两根火柴棍,可得:

个数1 2 3 4···n根数3 3+2 3+2+2 3+2+2+2···3+2+2+2+ ···+2■　■■　■n−1

表达式:3+2(n−1)=2n+1.

②每个三角形由三根火柴棍组成,从第一个图形起,火柴棍根数等于所含三角形个数乘3,再减去重复的火柴棍根数,可得:

个数1 2 3 4···n根数1×3 2×3−1 3×3−2 4×3−3···3×n−(n−1)

表达式:3n−(n−1)=2n+1.

③从第一个图形起,以一根火柴棍为基础,每增加一个三角形,增加两根火柴棍,可得:

个数1 2 3 4···n根数1+2 1+2+2 1+2+2+2 1+2+2+2+2···1+2+2+2+ ···+2■　■■　■n

表达式:1+2n.

④观察火柴棍的根数与三角形的个数的对应关系,可得:

个数1 2 3 4···n根数3=1×2+1 5=2×2+1 7=3×2+1 9=4×2+1···n×2+1

表达式:2n+1.

⑤将组成图形的火柴棍分为“横”放和“斜”放两类统计计数,可得:

个数1 2 3 4···n根数1+2 2+3 3+4 4+5···n+n+1

表达式:n+(n+1)=2n+1.

3　微课应用的思考

3.1　微课教学是时代的趋势

21世纪是知识“信息化”的时代,个性化学习和多样化学习已成为信息时代教育发展的重要特征.在落实《国家中长期教育改革与发展规划纲要(2010-2020年)》和实施《教育信息化十年发展规划(2011-2020年)》之际,在混合学习和移动学习日益盛行的趋势下,微课教学应运而生,顺应了学习方式多样化和个性化的趋势,.学习者通过微型移动互联网设备随时随地进行学习的要求,无论在家中、在学校里,还是在路上都能进行微课的学习,实现“人人能学、处处能学、时时能学”的学习环境,很好的满足学习者的微型学习、移动学习、个性化学习的需求.

3.2　让微课教学助力传统教学

《义务教育数学课程标准(2011版)》指出:“要充分考虑信息技术对数学学习内容和方式的影响,开发并向学生提供丰富的学习资源,把现代信息技术作为学生学习数学和解决问题的有力工具,有效地改进教与学的方式,使学生乐意并有可能投入到现实的、探索性的数学活动中去.”数学课程与信息技术的结合越来越多,信息技术与数学教学活动的整合也越来越受到教师的关注.信息技术为学生的学习提供了有力的学习工具,激发了学生探索研究数学的积极性和主动性.微课不仅大大缩减了学习者的学习时间,减轻了学生的学习压力和负担,而且就像有一位老师在身边一样,短短的几分钟就可以把遇到的问题自行解决,让学生的学习不再遇到绊脚石.因此,微课是传统课堂教学的一种有益的补充,甚至可能彻底改变学习者的学习方式.

3.3　灵活使用微课以增强教学实践性

《义务教育数学课程标准(2011年版)》指出:数学教学活动,特别是课堂教学应激发学生兴趣,调动学生积极性,引发学生的数学思考,学生学习应当是一个生动活泼的、主动的和富有个性的过程.教师是制作微课的主体,为了充分调动学生的学习积极性,可以鼓励与指导学生自主实践,制作微课解决知识点的学习.微课不应停留在内容的传递层面,更应注重教学活动的设计和活动过程的记录与思考.要实现这一转变,必须发挥学生的积极性和创造性,教师从理念与实践上加以培养与指导.

教师应当灵活使用微课,有效发挥其教学价值,要根据教材内容综合运用讲授法、实践法、探究学习法等,因课制宜,实现教学方式多元化;要设计出目标明确、形式生动、内容科学的微课,给课堂教学带来新活力,必将有效地调动学生学习的积极性、主动性,提高学生的创造性.

[1]徐晴.微课运用的实践与思考-以“价格变动的影响”教学为例[J],《中学政治教学参考》(西安),2015,(8)18-20.

[2]人民教育出版社,课程教材研究所,中学数学课程教材研究开发中心.义务教育教科书教师用书数学(七年级上册)[M],北京:人民教育出版社,2012.

[3]彭伟坚.微课在初中数学教学中的应用[J],中学数学研究(广州),2014,(9下):27-28.

[4]胡铁生.“微课”区域教育信息资源发展的新趋势[J],电化教育研究,2011,(10).