空基多雷达航迹抗差关联算法

齐林,刘瑜，任华龙，何友

1. 海军航空大学 信息融合研究所，烟台 264001 2. 海军青岛雷达声呐修理厂，青岛 266000

航迹关联是分布式多雷达数据融合[1-2]的一项关键技术，用于判别不同雷达上报的同源航迹，得到观测环境清晰完整的态势信息。航迹关联是系统误差配准[3-4]和态势融合的前提，同时系统误差的影响使估计航迹与真实航迹存在较大偏差，需要误差配准技术对量测数据进行校正。因此，系统误差存在时的航迹关联和误差配准互为前提，给问题的解决带来更大困难。

实际情况下，系统误差普遍存在于雷达量测数据中。特别是处于高速高机动运动状态的空基雷达，系统误差受到多种因素的影响，统计特性未知。传统航迹关联算法[5-7]仅考虑随机误差的影响，假设目标运动状态估计服从以真实运动状态为期望的高斯分布，此类算法在系统误差存在时效果恶化严重。

文献[8-12]提出基于参照拓扑特征的航迹关联算法(RET算法)用于处理雷达航迹抗差关联问题。算法认为在全局直角坐标系中，目标间相对位置关系不受系统误差的影响，以此作为航迹关联的依据。此类算法存在一定的缺陷。第一，系统误差是距离和角度上的量测偏差，经坐标变换到以融合中心为原点的全局直角坐标系中，系统误差不再体现为位置上的固定偏差。第二，拓扑关联基于多维分配准则处理多义性问题，但无法给出理论上的航迹关联门限，造成错误关联率较高。

由于航迹关联和误差配准互为前提，分别处理难度较大，文献[13-14]提出同时实施关联和配准的方法。单纯基于目标运动特征的航迹关联技术存在性能不稳定等问题，Mori等将目标属性等特征信息加入状态矢量，提出特征辅助航迹关联方法[15-16]。上述两类方法因计算复杂和属性信息缺失实用性受限。

文献[17]提出一种计算流程简便、适用于工程实践的基于距离检测的自动识别系统(Automatic Identification System, AIS)和对海雷达航迹抗差关联算法，在目标稀疏环境下性能良好，在目标密集环境下性能较差。

文献[18-19]基于等价量测一阶泰勒展开推导全局直角坐标系中状态估计矢量分解方程。文献[20]在此基础上定义航迹距离矢量，基于系统误差矢量对消得到两雷达航迹抗差关联条件，该算法具有较高的关联准确性和复杂环境适应能力。

大多现有的航迹抗差关联算法仅适用于两雷达环境，但两个以上雷达航迹间的融合处理在实际应用中普遍存在。多雷达数据融合情况下，为减少雷达两两关联产生的冗余计算，需要研究适用于两个以上雷达的航迹抗差关联算法。本文在航迹距离矢量的基础上推导适用于3个及3个以上雷达的航迹关联条件和多雷达航迹关联流程，提出空基多雷达航迹抗差关联算法。

1 问题描述

空基多平台信息融合系统中，每个运动平台搭载雷达探测跟踪环境中的多个运动目标，形成各自的环境态势信息，并基于航迹关联技术解决重叠覆盖空间中的去重复跟踪问题。假设环境中有若干个雷达和目标，其中目标T分别为雷达a、b、c探测到的第i、j、k个目标，某时刻雷达与目标的位置分布情况如图 1所示。

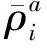
(1)

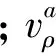
(2)

雷达b、c对T的量测矢量同理可知。

运动平台不能作为目标跟踪坐标系的原点，通常选择平台外一固定点作为目标跟踪惯性坐标系的原点。图 2中Oa(xoa,yoa)表示雷达a选取的固定参考点，将雷达量测转换到以Oa(xoa,yoa)为原点的惯性坐标系中，基于转换量测Kalman滤波[21]得到目标状态估计。空基多平台侦察监视环境存在探测距离远、目标分布密集、系统误差时变、雷达上报目标不一致等复杂情况，传统航迹关联算法失效；现有的航迹抗差关联算法大多仅适用于两雷达环境，需研究适用于两个以上雷达的航迹抗差关联算法。

2 算法描述

2.1 航迹距离矢量

在以融合中心O(0,0)为原点的全局直角坐标系中，状态估计矢量分解方程如式(3)所示，推导流程见文献[18-19]。

(3)

(4)

式(3)建立了全局直角坐标系下目标状态估计与目标真实状态、系统误差和随机误差之间的加性关系。文献[20]定义了航迹距离矢量:

(5)

(6)

式中：

(7)

(8)

(9)

2.2 3个雷达航迹关联条件

雷达a、b、c分别上报航迹i、j、k，航迹i分别与航迹j、k对消得到距离矢量，如果航迹i、j、k源自同一目标，则满足：

(10)

(11)

将4维等式(10)、等式(11)拆分成两个2维等式：

(12)

(13)

(14)

(15)

令

(16)

(17)

则

(18)

(19)

令

(20)

(21)

(22)

(23)

(24)

式中：nx为状态矢量的维数，这里nx=4。如果雷达a、b、c上报的航迹i、j、k源自同一目标，式(24)成立，否则不成立，因此可基于式(24)判断3个雷达上报航迹是否关联。

2.3 3个以上雷达航迹关联条件

讨论3个以上雷达航迹抗差关联条件，以四雷达情况为例。假设雷达a、b、c、d上报的航迹i、j、k、l，航迹i分别与航迹j、k、l对消得到距离矢量，如果航迹i、j、k、l源自同一目标，式(10)、式(11)和式(25)成立：

(25)

参照2.2节的推导，可知

(26)

(27)

(28)

(29)

式中：

(30)

(31)

(32)

理想情况下，式(24)、式(26)、式(28)中任意2式成立则第3式成立。将式(24)、式(26)、式(28)中任意2式成立作为航迹i、j、k、l关联的条件，如果3式中仅1式成立，判断该式包含的3条航迹关联，与第4条航迹不关联。

基于相同思路，容易将上述推导推广到4个以上雷达的情况。当雷达个数为m(m>2)时，判断每组雷达航迹是否关联需满足(m-1)(m-2)/2个条件。

2.4 多雷达航迹抗差关联流程

当雷达个数为m时，基于2.2节和2.3节的多雷达航迹关联条件分别判断不同雷达上报的m条航迹是否源自同一目标。然而雷达上报目标不一致的情况下，不同雷达上报的m条航迹的组合可能都不满足关联条件。此时需要降低组合中的航迹数，判断航迹个数为m-1的组合是否关联，直到为每个雷达至少找出一条航迹与其他雷达的航迹关联或组合中的航迹数降至2。实际上，航迹关联的目的是消除系统误差，得到清晰一致的环境态势。通过航迹关联处理能为每个与其他雷达有同源航迹的雷达准确的找到至少一条与其他雷达同源的航迹即可。

(33)

作为航迹i、j、k、l的关联代价，选取使全局代价最小的分配矩阵确定航迹的关联关系。

当雷达和目标数分别为m和n时，文献[20]所述两雷达航迹抗差关联算法，雷达两两关联的计算复杂度为

(34)

本文算法的计算复杂度为

Tpro(m,n)=(m-1)n2Td+

(35)

式中：Td为求一次4维距离矢量的计算复杂度;T4χ2为求一次4维χ2检验的计算复杂度，T2χ2为求一次2维χ2检验的计算复杂度。

当m>2、n>2时，Tt2t(m,n)>Tpro(m,n)，本文所述的多雷达航迹航迹抗差关联算法相比于雷达两两关联具有更低的计算复杂度，能显著降低雷达两两关联需要的冗余计算。

综上所述，空基多雷达航迹抗差关联流程如图3所示，其中对m条航迹的关联检验针对的是不同雷达上报的m条航迹，具体流程如图4所示。

3 仿真验证及结果分析

3.1 仿真环境设置及评价指标

为验证本文算法的性能，设置如下的仿真环境：某空域有飞行目标n=16批次，关联时刻目标位置在空域(x1,x2)×(y1,y2)中均匀分布，x1=100 km，x2=150 km，y1=100 km，y2=150 km。目标匀速等高飞行，水平面内初始速度v0和初始航向d0分别服从均匀分布，v0～U(100, 200) m/s，d0～U(0, 2)π rad，雷达采样周期T=4 s，航行周期数Time=100。

空基平台1的初始位置为(0, 5) km，初始速度为(150, 0) m/s，平台2的初始位置为(125, 0) km，初始速度为(0, 100) m/s，平台3的初始位置为(250, 0) km，初始速度为(0, 200) m/s。平台按初始速度做匀速直线运动，并向位置为(0, 0) m的融合中心实时上报估计航迹。运动平台不能作为目标跟踪的坐标系原点，雷达分别选取初始位置作为目标跟踪惯性坐标系的原点坐标。雷达量测随机误差分别服从均值为零，距离误差标准差σρ=100 m、方位角误差标准差σθ=0.3°的高斯分布。雷达系统误差时变，大小服从0到误差上限间的均匀分布，雷达1的误差上限Δρ1=-1 000 m、Δθ1=-1°，雷达2的误差上限Δρ2=0 m、Δθ2=0°，雷达3的误差上限Δρ3=1 000 m、Δθ3=1°。3个雷达分别上报14批次目标航迹，其中有10批次同源航迹。真实航迹与雷达估计航迹如图 5(a)所示，单个时刻目标真实点迹与雷达估计点迹如图 5(b)所示。

为描述算法的关联效果，这里定义航迹关联的评价指标。正确关联率为

(36)

错误关联率为

(37)

式中：n为一次实验中真实目标个数；n′为雷达上报的同源航迹个数，n′≤n；nca为正确关联的目标个数；nfa为错误关联的目标个数；Rca为正确关联率，即一次实验中正确关联的目标个数与同源航迹个数的比值；Rfa为错误关联率，即一次实验中错误关联的目标个数与真实目标个数的比值。实验结果由50次蒙特卡罗仿真求均值得到，Rca和Rfa分别为关联结果中的平均正确关联率和平均错误关联率。

为验证本文算法性能的优越性，在仿真环境中利用本文算法、基于目标参照拓扑特征的航迹关联算法(RET算法)和基于距离检测的可信关联算法(Confidential算法)实施航迹关联。RET算法以目标间相对位置关系作为关联依据，对系统误差和随机误差造成的目标位置偏差具有较强的适应性。Confidential算法是一种计算简便的工程化算法，在目标稀疏环境中性能良好。

3.2 目标密集环境适应性实验

为验证算法对环境中目标密集程度的适应能力，保持目标个数不变，改变目标分布空域的大小，比较3种算法的关联效果，如图6所示。

随着空域长度逐渐增大，目标密度逐渐减小，本文算法的Rca在70%上下浮动，Rfa接近于0。RET算法的Rca随目标密度减小由40%上升至95%再下降至50%，极值出现在空域长度为20 km时，Rfa由50%下降至接近于0。Confidential算法在空域长度小于40 km时性能较差，随着目标密度减小，性能逐渐提高。

本文算法基于状态估计矢量的分解对消构建χ2检验量，算法性能几乎不受目标密集程度的影响，具有较好的稳健性。RET算法基于目标参照拓扑特征实施航迹关联，在目标密集环境易将非同源航迹误判成同源航迹，造成Rca较低，Rfa较高。距离系统误差造成全局直角坐标系中目标间距伸缩，方位角相差越大的目标间距伸缩量越大。在目标稀疏环境中，互为参照的目标方位角相差较大，不同雷达上报的同源航迹参照拓扑特征不一致，RET算法Rca较低。Confidential算法要求一簇同源航迹周围没有异源航迹，适用于目标稀疏环境，在目标密集环境中性能较差。

3.3 随机误差适应性实验

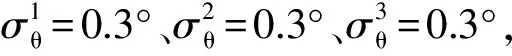
如图7(a)所示，距离误差标准差σρ由20 m增大至200 m，本文算法Rca由0逐渐增大至80%，Rfa接近于0。σρ由20 m增大至60 m，RET算法和Confidential 算法的Rca由35%增大至75%，σρ继续增大，Rca在75%上下浮动，RET算法的Rfa始终在5%上下浮动，Confidential 算法的Rfa始终在15%上下浮动。如图 7(b)所示，方位角误差标准差σθ由0.1°增大至1.0°，本文算法的Rca由0升高至75%再下降至10%，Rfa接近于0。RET算法和Confidential算法的Rca由80%左右逐渐下降至接近0，Rfa大于本文算法且随σθ增大而增大。

在一定的范围内，量测随机误差能抵消系统误差造成的航迹偏差，因此系统误差存在的条件下，3种算法的Rca随σρ增大而升高。σθ造成的航迹偏差远大于σρ，与雷达与目标间的距离成正比，σθ增大造成本文算法Rca先升高后降低，RET算法和Confidential算法的Rca降低明显。

3.4 系统误差适应性实验

为验证算法对系统误差的适应能力，分别改变仿真参数中雷达的距离、方位角系统误差上限，其他参数不变，比较本文算法和RET算法的关联效果。雷达方位角误差上限保持Δθ1=-1°、Δθ3=1°，距离误差上限Δρ1在-200～-2 000 m等间隔分布，Δρ3在200～2 000 m等间隔分布，得到如图 7(c)所示的关联结果；雷达距离误差上限保持Δρ1=-1 000 m、Δρ3=1 000 m，方位角误差上限Δθ1在-0.2°～-2.0°等间隔分布，Δθ3在0.2°～2.0°等间隔分布，得到如图 7(d)所示的关联结果。

由图 7(c)可知，距离误差上限Δρ由200 m增大至2000 m，本文算法、RET算法、Confidential算法的Rca分别在65%、75%、70%上下浮动，本文算法的Rfa接近0，RET算法的Rfa在5%上下浮动、Confidential算法的Rfa在15%上下浮动。由图 7(d)可知，方位角误差上限Δθ由0.2°增大至2.0°，3种算法的Rca均有显著下降，本文算法Rca最低。本文算法Rfa接近0；RET算法的Rfa在5%上下浮动；Confidential算法的Rfa由5%上升至27%。

距离系统误差造成的航迹偏差较小，3种算法均对其有较强的适应性；方位角系统误差造成的航迹偏差较大，随着方位角系统误差增大，3种算法性能都有显著下降。本文算法基于状态估计矢量分解对消推导多雷达航迹关联条件，优点是能排除大部分非同源航迹，Rfa较低，缺点是门限比较严格导致方位角系统误差较大时Rca较低。RET算法基于多维分配处理多义性问题，没有严格的关联门限，导致Rca和Rfa都比较高。

4 结 论

本文基于高斯随机矢量统计特性推导出一种适用于复杂环境的空基多雷达航迹抗差关联算法。

1) 本文算法能显著减低多雷达情况下雷达两两关联产生的冗余计算，计算复杂度较低。

2) 本文算法基于状态估计矢量分解对消严格推导航迹关联门限，在目标密集等复杂环境下仍能排除大部分非同源航迹，具有很低的错误关联率，缺点是门限比较严格导致方位角系统误差较大时正确关联率较低。

3) 雷达量测系统误差和随机误差都存在且系统误差较大时，由于随机误差对系统误差的抵消作用，航迹关联正确率随随机误差增大而提高。

参 考 文 献

[1] BAR-SHALOM Y, FORTMANN T E. Tracking and data association[M]. Orlando: Academic Press INC., 1988: 266-272.

[2] 何友， 王国宏， 关欣. 信息融合理论及应用[M]. 北京: 电子工业出版社, 2010: 267-308.

HE Y, WANG G H, GUAN X. Information fusion theory with applications[M]. Beijing: Publishing House of Electronics Industry, 2010: 267-308 (in Chinese).

[3] LIN X D, BAR-SHALOM Y, KIRUBARAJAN T. Exact multi-sensor dynamic bias estimation with local tracks[J]. IEEE Transactions on Aerospace & Electronic Systems, 2004, 40(2): 576-590.

[4] ZHENG Z W, ZHU Y S. New least squares registration algorithm for data fusion[J]. IEEE Transactions on Aerospace & Electronic Systems, 2004, 40(4): 1410-1416.

[5] HE Y, ZHANG J W. New track correlation algorithms in a multi-sensor data fusion system[J]. IEEE Transactions on Aerospace & Electronic Systems, 2006, 42(4):1359-1371.

[6] 何友， 宋强， 熊伟. 基于傅里叶变换的航迹对准关联算法[J]. 航空学报, 2010, 31(2): 356-362.

HE Y, SONG Q, XIONG W. A track registration-correlation algorithm based on Fourier transform[J]. Acta Aeronautica et Astronautica Sinica, 2010, 31(2): 356-362 (in Chinese).

[7] 衣晓， 张怀巍， 曹昕莹， 等. 基于区间灰数的分布式多目标航迹关联算法[J]. 航空学报, 2013, 34(2): 352-360.

YI X, ZHANG H W, CAO X Y, et al. A track association algorithm for distributed multi-target systems based on gray interval numbers[J]. Acta Aeronautica et Astronautica Sinica, 2013, 34(2): 352-360 (in Chinese).

[8] 石玥， 王钺， 王树刚， 等. 基于目标参照拓扑的模糊航迹关联方法[J]. 国防科技大学学报, 2006, 28(4): 105-109.

SHI Y, WANG Y, WANG S G, et al. Fuzzy data association based on target topology of reference[J]. Journal of National University of Defence Technology, 2006, 28(4): 105-109 (in Chinese).

[9] TIAN W, WANG Y, SHAN X M, et al. Track-to-track association for biased data based on the reference topology feature[J]. IEEE Signal Processing Letters, 2014, 21(4): 449-453.

[10] 田威. 复杂环境下多传感器航迹关联与抗差处理[D]. 北京: 清华大学, 2014: 96-116.

TIAN W. Multi-sensor track-to-track association and bias removal in complex environments[D]. Beijing: Tsinghua University, 2014: 96-116 (in Chinese).

[11] ZHU H Y, HAN S Y. Track-to-track association based on structural similarity in the presence of sensor biases[J]. Journal of Applied Mathematics, 2014(1): 1-8.

[12] ZHU H Y, WANG W, WANG C. Robust track-to-track association in the presence of sensor biases and missed detections[J]. Information Fusion, 2016, 27: 33-40.

[13] LI Z, CHEN S, LEUNG H, et al. Joint data association, registration, and fusion using EM-KF[J]. IEEE Transactions on Aerospace & Electronic Systems, 2010, 46(2): 496-507.

[14] ZHU H, LEUNG H, YUEN K. A joint data association, registration, and fusion approach for distributed tracking[J]. Information Sciences, 2015, 324(C):186-196.

[15] MORI S, CHANG K C, CHONG C Y. Tracking performance evaluation-prediction of track purity[C]∥Proceeding of SPIE. Bellingham, WA: SPIE, 1989: 215-223.

[16] MORI S, CHANG K C, CHONG C Y. Performance prediction of feature-aided track-to-track association[J]. IEEE Transactions on Aerospace & Electronic Systems, 2014, 50(4): 2593-2603.

[17] 齐林， 崔亚奇， 熊伟， 等. 基于距离检测的自动识别系统和对海雷达航迹抗差关联算法[J]. 电子与信息学报, 2015, 37(8): 1855-1861.

QI L, CUI Y Q, XIONG W, et al. Anti-bias association algorithm for automatic identification system and radar based on bias detection[J]. Journal of Electronics & Information Technology, 2015, 37(8): 1855-1861 (in Chinese).

[18] ZHU H Y, CHEN S. Track fusion in the presence of sensor biases[J]. IET Signal Process, 2014, 8(9): 958-967.

[19] ZHU H Y, WANG C. Joint track-to-track association and sensor registration at the track level[J]. Digital Signal Processing, 2015, 41: 48-59.

[20] QI L, DONG K, LIU Y, et al. Anti-bias track-to-track association algorithm based on distance detection[J]. IET Radar, Sonar & Navigation, 2017, 11(2): 269-276.

[21] 何友， 修建娟， 关欣. 雷达数据处理及应用[M]. 3版. 北京: 电子工业出版社, 2013: 36-50.

HE Y, XIU J J, GUAN X. Radar data processing with applications[M]. 3rd ed. Beijing: Publishing House of Electronics Industry, 2013: 36-50 (in Chinese).